浅谈组合数学
分类加法计数原理:
完成一件事可以有n类方案,第一类方案有$m_{1}$种方法,第二类有$m_{2}$种方法......那么完成这件事情的方法有
N = $m_{1}$+$m_{2}$+...+$m_{n}$
注意----每类方法都能独立地完成事件,且一步到位(有点像物理的并联电路)
分步计数原理:
完成一件事情有n个步骤,第一步有$m_{1}$种不同方法,第二步有$m_{2}$种不同方法......那么完成这件事情的方法有
N = $m_{1}$*$m_{2}$*...*$m_{n}$
注意---缺少任何一个步骤事件都完不成,且要逐步到位(有点像物理的串联电路)
判断是分类还是分步要看可不可以一步到位。
排列
线排列:(选,排) 【排列】
定义——从n个不同元素中,选出m个(m<=n) 个元素,按照一定的顺序排成一列,叫做从n个不同
元素中取出m个元素的一个线排列。
其中 1.元素不能重复 2.按照一定的顺序 3.两个排列相同,指的是元素和顺序都完全相同
特别地,当m = n 时,这样的线排列叫做全排列。
排列数: 【数】
从n个不同的元素中,任取m个元素的所有排列的个数。
$A^{m}_{n}=n*(n-1)*(n-2)*...*(n-m+1)=\frac{n!}{(n-m)!}$
我们将其具象化为:
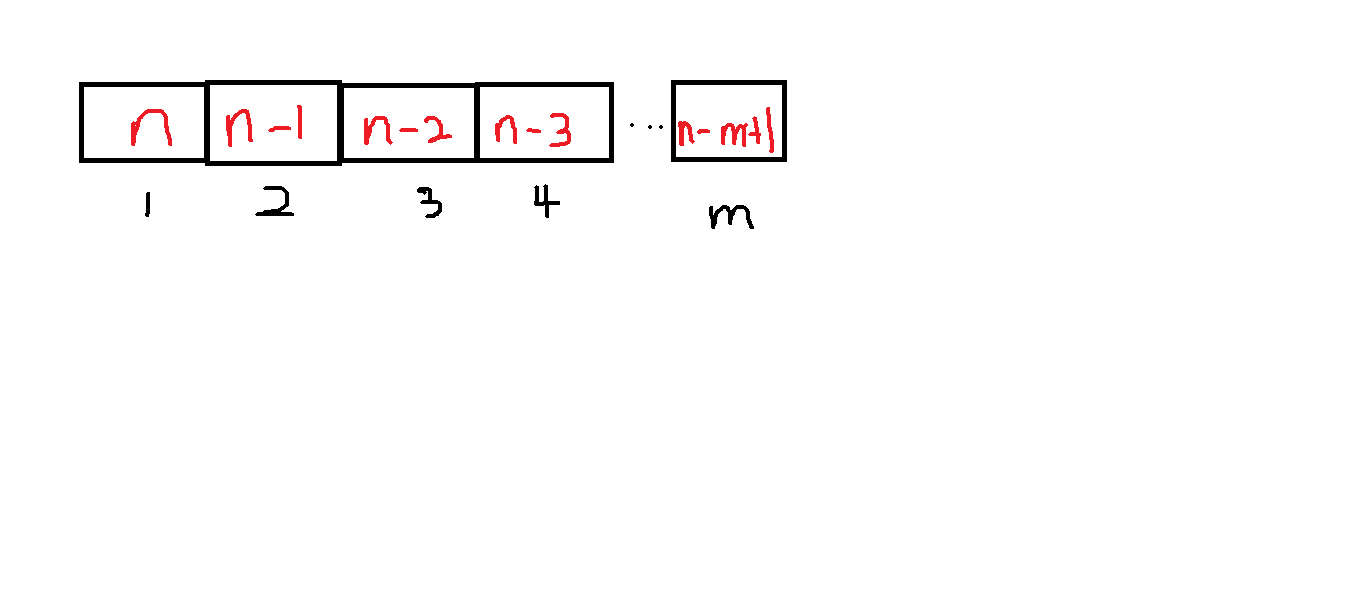
第一位有n种选法,第二种就有n-1种选法。。。。。。根据分步计数原理就可以得出排列数公式。
同时,全排列就是 $A^{n}_{n}=\frac{n!}{n!}$
其中0!=1
在面对有限制条件的排列时,我们可以优先将特殊元素进行考虑,并运用分类和分步计数原理去解决。
(以下部分资料取自《信息奥赛一本通》)
相异元素可重排列:
从n个不同元素中可以重复抽取m个元素的排列,叫做相异元素的可重复排列,即
N = n * n * n... =$n^{m}$
不全相异元素的排列:
如果在n个元素中,有$n_{1}$个彼此相同,有$n_{2}$个元素彼此相同......有$n_{m}$个元素彼此相同,且$n_{1}$+$n_{2}$+$n_{3}$+......+$n_{m}$=n,则这n个元素的全排列叫做不全相异元素的全排列。
则其排列数公式为 $\frac{n!}{n_{1}!*n_{2}!*...*n_{m}!}$
这个的理解可以参考一下棋盘多项式???
组合
非重组合:
字面意思,就是从n个元素中选取m个元素,(m<=n),当然这m个元素不可重复,就叫做从n个元素中取
出m个元素的非重组合。且与排列不同的是,它不考虑是否有序,例如:
组合--{A,B,C} 排列--{A,B,C},{A,C,B},{B,A,C},{B,C,A},{C,A,B},{C,B,A}
我们记组合数为$C^{m}_{n}$表示,则根据分步计数原理得,$P^{m}_{n}=C^{m}_{n}*P^{m}_{m}$
所以组合数公式就可以推导了:
$C^{m}_{n}=\frac{P^{m}_{n}}{P^{m}_{m}}=\frac{n!}{m!(n-m)!} n,m∈N*$
其中组合数有俩性质:1.$C^{0}_{n}=1$,$C^{n}_{n}=1$,且$C^{m}_{n}=C^{n-m}_{n}$
(待理解) 2.$C^{m}_{n+1}=C^{m}_{n}+C^{m-1}_{n}$
可重复组合+二项式定理后面再来。。。


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步