Machine Learning 22 二分类实例
分类问题项目流程:
- 如何端到端的完成一个分类问题的模型
- 如何通过数据转换提高模型的准确度
- 如何通过调参提高模型的准确度
- 如何通过算法集成提高模型的准确度
问题定义
在这个项目中采用声纳、矿山和岩石数据集(http://archive.ics.uci.edu/ml/datasets/Connectionist+Bench+%28Sonar%2C+Mines+vs.+Rocks%29)。通过声纳返回的信息判断物质是金属还是岩石。这个数据集共有208条记录,每条记录了60中不同的声纳探测数据和一个分类结果,若是岩石则标记为R,若是金属则标记为M。
导入数据
在导入之前,先需要导入所需的类库。
1 #60中声纳探测预测 2 import numpy as np 3 from matplotlib import pyplot 4 from pandas import read_csv 5 from pandas import set_option 6 from pandas.plotting import scatter_matrix 7 from sklearn.preprocessing import StandardScaler 8 from sklearn.model_selection import train_test_split 9 from sklearn.model_selection import KFold 10 from sklearn.model_selection import cross_val_score 11 from sklearn.model_selection import GridSearchCV 12 from sklearn.metrics import classification_report 13 from sklearn.metrics import confusion_matrix 14 from sklearn.metrics import accuracy_score 15 from sklearn.pipeline import Pipeline 16 from sklearn.linear_model import LogisticRegression 17 18 from sklearn.tree import DecisionTreeClassifier 19 from sklearn.discriminant_analysis import LinearDiscriminantAnalysis 20 from sklearn.neighbors import KNeighborsRegressor 21 from sklearn.tree import DecisionTreeClassifier 22 from sklearn.naive_bayes import GaussianNB 23 from sklearn.svm import SVC 24 25 from sklearn.ensemble import RandomForestClassifier 26 from sklearn.ensemble import GradientBoostingClassifier 27 from sklearn.ensemble import ExtraTreesClassifier 28 from sklearn.ensemble import AdaBoostClassifier 29 30 #导入数据 31 filename='/home/aistudio/work/sonar.all-data.csv' 32 dataset=read_csv(filename,header=None)
因为每条记录都是60种不同的声纳探测结果,没有办法提供合适的名字,所以导入时没有指定特征属性名。
数据理解
先确认数据的维度,例如记录的条数和数据特征属性的个数:
1 #数据维度 2 print(dataset.shape)
执行结果显示数据有208条记录和61个数据特征属性(包含60此声纳探测数据和一个分类结果)。
(208, 61)
接下来看一下各个数据特征和数据类型。
1 #查看数据类型 2 set_option('display.max_rows',500) 3 print(dataset.dtypes)
结果显示所有的特征属性的数据类型都是数字。

1 0 float64 2 1 float64 3 2 float64 4 3 float64 5 4 float64 6 5 float64 7 6 float64 8 7 float64 9 8 float64 10 9 float64 11 10 float64 12 11 float64 13 12 float64 14 13 float64 15 14 float64 16 15 float64 17 16 float64 18 17 float64 19 18 float64 20 19 float64 21 20 float64 22 21 float64 23 22 float64 24 23 float64 25 24 float64 26 25 float64 27 26 float64 28 27 float64 29 28 float64 30 29 float64 31 30 float64 32 31 float64 33 32 float64 34 33 float64 35 34 float64 36 35 float64 37 36 float64 38 37 float64 39 38 float64 40 39 float64 41 40 float64 42 41 float64 43 42 float64 44 43 float64 45 44 float64 46 45 float64 47 46 float64 48 47 float64 49 48 float64 50 49 float64 51 50 float64 52 51 float64 53 52 float64 54 53 float64 55 54 float64 56 55 float64 57 56 float64 58 57 float64 59 58 float64 60 59 float64 61 60 object 62 dtype: object
再查看最开始的20条记录:
1 #查看最开始的20条记录 2 set_option('display.width',100) 3 print(dataset.head(20))

1 0 1 2 3 4 5 6 7 8 9 ... 51 \ 2 0 0.0200 0.0371 0.0428 0.0207 0.0954 0.0986 0.1539 0.1601 0.3109 0.2111 ... 0.0027 3 1 0.0453 0.0523 0.0843 0.0689 0.1183 0.2583 0.2156 0.3481 0.3337 0.2872 ... 0.0084 4 2 0.0262 0.0582 0.1099 0.1083 0.0974 0.2280 0.2431 0.3771 0.5598 0.6194 ... 0.0232 5 3 0.0100 0.0171 0.0623 0.0205 0.0205 0.0368 0.1098 0.1276 0.0598 0.1264 ... 0.0121 6 4 0.0762 0.0666 0.0481 0.0394 0.0590 0.0649 0.1209 0.2467 0.3564 0.4459 ... 0.0031 7 5 0.0286 0.0453 0.0277 0.0174 0.0384 0.0990 0.1201 0.1833 0.2105 0.3039 ... 0.0045 8 6 0.0317 0.0956 0.1321 0.1408 0.1674 0.1710 0.0731 0.1401 0.2083 0.3513 ... 0.0201 9 7 0.0519 0.0548 0.0842 0.0319 0.1158 0.0922 0.1027 0.0613 0.1465 0.2838 ... 0.0081 10 8 0.0223 0.0375 0.0484 0.0475 0.0647 0.0591 0.0753 0.0098 0.0684 0.1487 ... 0.0145 11 9 0.0164 0.0173 0.0347 0.0070 0.0187 0.0671 0.1056 0.0697 0.0962 0.0251 ... 0.0090 12 10 0.0039 0.0063 0.0152 0.0336 0.0310 0.0284 0.0396 0.0272 0.0323 0.0452 ... 0.0062 13 11 0.0123 0.0309 0.0169 0.0313 0.0358 0.0102 0.0182 0.0579 0.1122 0.0835 ... 0.0133 14 12 0.0079 0.0086 0.0055 0.0250 0.0344 0.0546 0.0528 0.0958 0.1009 0.1240 ... 0.0176 15 13 0.0090 0.0062 0.0253 0.0489 0.1197 0.1589 0.1392 0.0987 0.0955 0.1895 ... 0.0059 16 14 0.0124 0.0433 0.0604 0.0449 0.0597 0.0355 0.0531 0.0343 0.1052 0.2120 ... 0.0083 17 15 0.0298 0.0615 0.0650 0.0921 0.1615 0.2294 0.2176 0.2033 0.1459 0.0852 ... 0.0031 18 16 0.0352 0.0116 0.0191 0.0469 0.0737 0.1185 0.1683 0.1541 0.1466 0.2912 ... 0.0346 19 17 0.0192 0.0607 0.0378 0.0774 0.1388 0.0809 0.0568 0.0219 0.1037 0.1186 ... 0.0331 20 18 0.0270 0.0092 0.0145 0.0278 0.0412 0.0757 0.1026 0.1138 0.0794 0.1520 ... 0.0084 21 19 0.0126 0.0149 0.0641 0.1732 0.2565 0.2559 0.2947 0.4110 0.4983 0.5920 ... 0.0092 22 23 52 53 54 55 56 57 58 59 60 24 0 0.0065 0.0159 0.0072 0.0167 0.0180 0.0084 0.0090 0.0032 R 25 1 0.0089 0.0048 0.0094 0.0191 0.0140 0.0049 0.0052 0.0044 R 26 2 0.0166 0.0095 0.0180 0.0244 0.0316 0.0164 0.0095 0.0078 R 27 3 0.0036 0.0150 0.0085 0.0073 0.0050 0.0044 0.0040 0.0117 R 28 4 0.0054 0.0105 0.0110 0.0015 0.0072 0.0048 0.0107 0.0094 R 29 5 0.0014 0.0038 0.0013 0.0089 0.0057 0.0027 0.0051 0.0062 R 30 6 0.0248 0.0131 0.0070 0.0138 0.0092 0.0143 0.0036 0.0103 R 31 7 0.0120 0.0045 0.0121 0.0097 0.0085 0.0047 0.0048 0.0053 R 32 8 0.0128 0.0145 0.0058 0.0049 0.0065 0.0093 0.0059 0.0022 R 33 9 0.0223 0.0179 0.0084 0.0068 0.0032 0.0035 0.0056 0.0040 R 34 10 0.0120 0.0052 0.0056 0.0093 0.0042 0.0003 0.0053 0.0036 R 35 11 0.0265 0.0224 0.0074 0.0118 0.0026 0.0092 0.0009 0.0044 R 36 12 0.0127 0.0088 0.0098 0.0019 0.0059 0.0058 0.0059 0.0032 R 37 13 0.0095 0.0194 0.0080 0.0152 0.0158 0.0053 0.0189 0.0102 R 38 14 0.0057 0.0174 0.0188 0.0054 0.0114 0.0196 0.0147 0.0062 R 39 15 0.0153 0.0071 0.0212 0.0076 0.0152 0.0049 0.0200 0.0073 R 40 16 0.0158 0.0154 0.0109 0.0048 0.0095 0.0015 0.0073 0.0067 R 41 17 0.0131 0.0120 0.0108 0.0024 0.0045 0.0037 0.0112 0.0075 R 42 18 0.0010 0.0018 0.0068 0.0039 0.0120 0.0132 0.0070 0.0088 R 43 19 0.0035 0.0098 0.0121 0.0006 0.0181 0.0094 0.0116 0.0063 R 44 45 [20 rows x 61 columns]
数据的描述性统计信息:
1 #描述统计信息 2 set_option('precision',3) 3 print(dataset.describe())
可以看到,数据具有相同的范围,但是中位值不同,这也许对数据正太化的结果有正面的影响。

1 0 1 2 3 4 5 6 7 8 9 \ 2 count 208.000 2.080e+02 208.000 208.000 208.000 208.000 208.000 208.000 208.000 208.000 3 mean 0.029 3.844e-02 0.044 0.054 0.075 0.105 0.122 0.135 0.178 0.208 4 std 0.023 3.296e-02 0.038 0.047 0.056 0.059 0.062 0.085 0.118 0.134 5 min 0.002 6.000e-04 0.002 0.006 0.007 0.010 0.003 0.005 0.007 0.011 6 25% 0.013 1.645e-02 0.019 0.024 0.038 0.067 0.081 0.080 0.097 0.111 7 50% 0.023 3.080e-02 0.034 0.044 0.062 0.092 0.107 0.112 0.152 0.182 8 75% 0.036 4.795e-02 0.058 0.065 0.100 0.134 0.154 0.170 0.233 0.269 9 max 0.137 2.339e-01 0.306 0.426 0.401 0.382 0.373 0.459 0.683 0.711 10 11 ... 50 51 52 53 54 55 56 \ 12 count ... 208.000 2.080e+02 2.080e+02 208.000 2.080e+02 2.080e+02 2.080e+02 13 mean ... 0.016 1.342e-02 1.071e-02 0.011 9.290e-03 8.222e-03 7.820e-03 14 std ... 0.012 9.634e-03 7.060e-03 0.007 7.088e-03 5.736e-03 5.785e-03 15 min ... 0.000 8.000e-04 5.000e-04 0.001 6.000e-04 4.000e-04 3.000e-04 16 25% ... 0.008 7.275e-03 5.075e-03 0.005 4.150e-03 4.400e-03 3.700e-03 17 50% ... 0.014 1.140e-02 9.550e-03 0.009 7.500e-03 6.850e-03 5.950e-03 18 75% ... 0.021 1.673e-02 1.490e-02 0.015 1.210e-02 1.058e-02 1.043e-02 19 max ... 0.100 7.090e-02 3.900e-02 0.035 4.470e-02 3.940e-02 3.550e-02 20 21 57 58 59 22 count 2.080e+02 2.080e+02 2.080e+02 23 mean 7.949e-03 7.941e-03 6.507e-03 24 std 6.470e-03 6.181e-03 5.031e-03 25 min 3.000e-04 1.000e-04 6.000e-04 26 25% 3.600e-03 3.675e-03 3.100e-03 27 50% 5.800e-03 6.400e-03 5.300e-03 28 75% 1.035e-02 1.033e-02 8.525e-03 29 max 4.400e-02 3.640e-02 4.390e-02 30 31 [8 rows x 60 columns]
最后看一下数据的分类分布:
1 #数据的分类与分布 2 print(dataset.groupby(60).size())
60 M 111 R 97 dtype: int64
数据可视化
1 #直方图 2 dataset.hist(sharex=False,sharey=False,xlabelsize=1,ylabelsize=1) 3 pyplot.show()
下图中显示,大部分数据呈高斯分布或指数分布
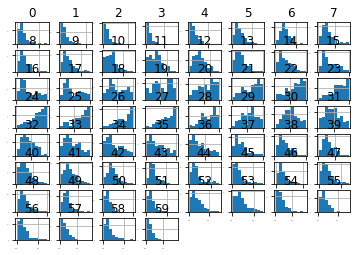
接下来看下密度分布图:
1 #密度图 2 dataset.plot(kind='density',subplots=True,layout=(8,8),sharex=False,legend=False, fontsize=1) 3 pyplot.show()
可以看到大部分数据呈现一定程度的偏态分布,也许通过Box-Cox转换可以提高模型的准确度。
Box-Cox转换是统计中常用的一种数据变化方式,用于连续响应变量不满足正太分布的情况。Box-Cox转换后,可以在一定程度上减少不可观测的误差,也可以预测变量的相关性,将数据转换成正太分布。

接下来看一下数据特征的两两相关性:
1 #关系矩阵图 2 fig=pyplot.figure() 3 ax=fig.add_subplot(111) 4 cax=ax.matshow(dataset.corr(),vmin=-1,vmax=1,interpolation='none') 5 fig.colorbar(cax) 6 pyplot.show()
可以看到数据有一定的负先关性:
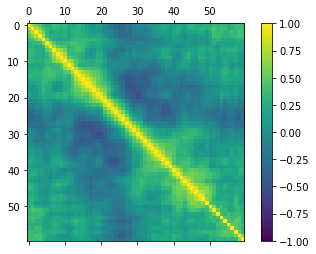
分离评估数据集
按照常规,2:8分:
1 #分离评估数据集 2 array=dataset.values 3 x=array[:,0:60].astype(float) 4 y=array[:,60] 5 validation_size=0.2 6 seed=7 7 x_train,x_validation,y_train,y_validation=train_test_split(x,y,test_size=validation_size,random_state=seed)
评估算法
采用10折交叉验证来分离数据,并通过准确度来比较算法,这样可以很快的找到最优算法:
1 #评估算法--评估标准 2 num_folds=10 3 seed=7 4 scoring='accuracy'
同上一节一样,首先利用原始数据对算法进行审查,下面会选择六种不同的算法进行审查。
线性算法:罗辑回归(LR)和线性判别分析(LDA)
非线性算法:分类与回归树算法(CART),支持向量机(SVM),贝叶斯分类器(NB)和K近邻(KNN)
算法模型初始化代码如下:
1 models={} 2 models['LR']=LogisticRegression() 3 models['LDA']=LinearDiscriminantAnalysis() 4 models['KNN']=KNeighborsClassifier() 5 models['CART']=DecisionTreeClassifier() 6 models['NB']=GaussianNB() 7 models['SVM']=SVC()
对所有的算法都不进行调参,使用默认的参数来比较算法。通过比较准确度的平均值和标准方差来比较算法:
1 results=[] 2 for key in models: 3 kfold=KFold(n_splits=num_folds,random_state=seed) 4 cv_results=cross_val_score(models[key],x_train,y_train,cv=kfold,scoring=scoring) 5 results.append(cv_results) 6 print('%s: %f (%f)' % (key,cv_results.mean(),cv_results.std()))
执行结果显示,逻辑回归算法(LR)和K近邻(KNN)值得我们进一步分析。
LR: 0.782721 (0.093796) LDA: 0.746324 (0.117854) KNN: 0.808088 (0.067507) CART: 0.727941 (0.102731) NB: 0.648897 (0.141868) SVM: 0.608824 (0.118656)
这只是K折交叉验证给出的平均统计结果,通常还要看每次得出的结果分布状况。在这里使用箱线图来显示数据分布。
1 #评估算法----箱线图 2 fig=pyplot.figure() 3 fig.suptitle('Algorithm Comparison') 4 ax=fig.add_subplot(111) 5 pyplot.boxplot(results) 6 ax.set_xticklabels(models.keys()) 7 pyplot.show()
如下图所示,K近邻算法的执行结果分布比较紧凑,说明算法对数据的处理比较准确,但是,支持向量机(svm)的结果较差。
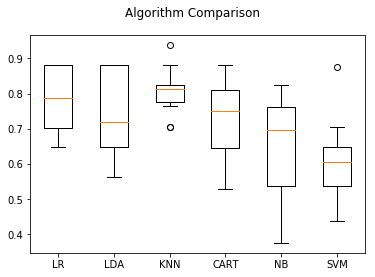
可能是数据分布的多样性导致SVM算法不够准确,接下来会对数据进行正太化,然后重新评估算法。
下面采用Pipeline来流程化处理:
1 #评估算法----正太化数据 2 pipelines={} 3 pipelines['ScalerLR']=Pipeline([('Scaler',StandardScaler()),('LR',LogisticRegression())]) 4 pipelines['ScalerLDA']=Pipeline([('Scaler',StandardScaler()),('LDA',LinearDiscriminantAnalysis())]) 5 pipelines['ScalerKNN']=Pipeline([('Scaler',StandardScaler()),('KNN',KNeighborsClassifier())]) 6 pipelines['ScalerCART']=Pipeline([('Scaler',StandardScaler()),('CART',DecisionTreeClassifier())]) 7 pipelines['ScalerNB']=Pipeline([('Scaler',StandardScaler()),('NB',GaussianNB())]) 8 pipelines['ScalerSVM']=Pipeline([('Scaler',StandardScaler()),('SVM',SVC())]) 9 10 results=[] 11 for key in pipelines: 12 kfold=KFold(n_splits=num_folds,random_state=seed) 13 cv_results=cross_val_score(pipelines[key],x_train,y_train,cv=kfold,scoring=scoring) 14 results.append(cv_results) 15 print('%s: %f (%f)' % (key,cv_results.mean(),cv_results.std()))
从执行结果来看,K近邻依然具有最好的结果,甚至还有所提高,同时SVM也得到了极大的提高。
ScalerLR: 0.734191 (0.095885) ScalerLDA: 0.746324 (0.117854) ScalerKNN: 0.825735 (0.054511) ScalerCART: 0.717647 (0.095103) ScalerNB: 0.648897 (0.141868) ScalerSVM: 0.836397 (0.088697)
再通过箱线图看看:
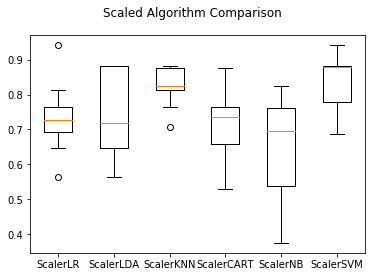
同样可以看到KNN和SVM的数据分布也是最紧凑的。
算法调参
下面就对KNN和SVM这两个算法进行调参,以进一步提高算法的准确度。
K近邻默认n_neighbors=5,下面对这个参数多试几组,采用相同的10折交叉验证来测试:
1 #调参改进算法--KNN 2 scaler=StandardScaler().fit(x_train) 3 rescaledX=scaler.transform(x_train) 4 param_grid={'n_neighbors':[1,3,5,7,9,11,13,15,17,19,21]} 5 model=KNeighborsClassifier() 6 kfold=KFold(n_splits=num_folds,random_state=seed) 7 grid=GridSearchCV(estimator=model,param_grid=param_grid,scoring=scoring,cv=kfold) 8 grid_result=grid.fit(X=rescaledX,y=y_train) 9 print('最优:%s 使用%s' % (grid_result.best_score_,grid_result.best_params_)) 10 cv_results = zip(grid_result.cv_results_['mean_test_score'],grid_result.cv_results_['std_test_score'],grid_result.cv_results_['params']) 11 for mean,std,param in cv_results: 12 print('%f (%f) with %r' % (mean, std, param))
执行结果如下:
最优:0.8493975903614458 使用{'n_neighbors': 1}
0.849398 (0.059881) with {'n_neighbors': 1}
0.837349 (0.066303) with {'n_neighbors': 3}
0.837349 (0.037500) with {'n_neighbors': 5}
0.765060 (0.089510) with {'n_neighbors': 7}
0.753012 (0.086979) with {'n_neighbors': 9}
0.734940 (0.104890) with {'n_neighbors': 11}
0.734940 (0.105836) with {'n_neighbors': 13}
0.728916 (0.075873) with {'n_neighbors': 15}
0.710843 (0.078716) with {'n_neighbors': 17}
0.722892 (0.084555) with {'n_neighbors': 19}
0.710843 (0.108829) with {'n_neighbors': 21}
得到最优的n_neighbors=1.
支持向量机有两个重要的参数,C(惩罚系数)和kernel(径向基函数),默认的C参数是1.0,kernal=rbf,下面将对这两个参数进行调参。
1 #SVM--调参 2 scaler=StandardScaler().fit(x_train) 3 rescaledX=scaler.transform(x_train).astype(float) 4 param_grid={} 5 param_grid['C']=[0.1,0.3,0.5,0.7,0.9,1.0,1.3,1.5,1.7,2.0] 6 param_grid['kernel']=['linear','poly','rbf','sigmoid','precomputed'] 7 model=SVC() 8 kfold=KFold(n_splits=num_folds,random_state=seed) 9 grid=GridSearchCV(estimator=model,param_grid=param_grid,scoring=scoring,cv=kfold) 10 grid_result=grid.fit(X=rescaledX, y=y_train) 11 print('最优:%s 使用%s' % (grid_result.best_score_,grid_result.best_params_)) 12 cv_results=zip(grid_result.cv_results_['mean_test_score'],grid_result.cv_results_['std_test_score'],grid_result.cv_results_['param']) 13 for mean, std, param in cv_results: 14 print('%f (%f) with %r' % (mean, std, param))
上面的代码调试过程中有误,但我找不出原因(Line 10: ValueError: X should be a square kernel matrix),为了这本书的完整性,我还是贴出错误的代码。
书中给出的测试结果:
最好的支持向量机SVM的参数是C=1.5,kernel=RBF。准确度达到0.8675,这也比K近邻算法的结果要好一些。
集成算法
下面会对四种集成算法进行比较,以便进一步提高算法的准确度。
装袋算法:随机森林(RF)和极端随机树(ET)
提升算法:AdaBoost(AB)和随机梯度上升(GBM)
依然采用10折交叉验证集成算法的准确度,以便选择最优的算法模型。
1 #集成算法 2 num_folds=10 3 scoring='accuracy' 4 5 ensembles={} 6 ensembles['ScaledAB']=Pipeline([('Scaler',StandardScaler()),('AB',AdaBoostClassifier())]) 7 ensembles['ScaledGBM']=Pipeline([('Scaler',StandardScaler()),('GBM',GradientBoostingClassifier())]) 8 ensembles['ScaledRF']=Pipeline([('Scaler',StandardScaler()),('RFR',RandomForestClassifier())]) 9 ensembles['ScaledET']=Pipeline([('Scaler',StandardScaler()),('ETR',ExtraTreesClassifier())]) 10 11 results=[] 12 for key in ensembles: 13 kfold=KFold(n_splits=num_folds,random_state=seed) 14 cv_result=cross_val_score(ensembles[key],x_train,y_train,cv=kfold,scoring=scoring) 15 results.append(cv_result) 16 print('%s: %f (%f)' % (key,cv_result.mean(),cv_result.std()))
执行结果如下:
ScaledAB: 0.813971 (0.066017) ScaledGBM: 0.847794 (0.100189) ScaledRF: 0.764338 (0.092898) ScaledET: 0.771691 (0.097858)
通过箱线图来看一下算法结果的离散状况。
1 #集成算法----箱线图 2 fig=pyplot.figure() 3 fig.suptitle('Scaled Algorithm Comparison') 4 ax=fig.add_subplot(111) 5 pyplot.boxplot(results) 6 ax.set_xticklabels(ensembles.keys()) 7 pyplot.show()
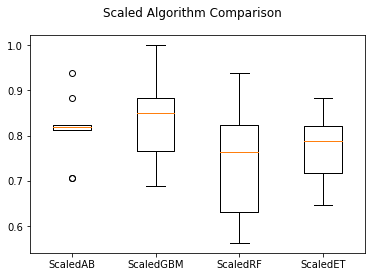
随机梯度上升(GBM)值得进一步分析,因为它具有良好的准确度,并且数据比较紧凑,接下来对其进行调参。
1 #集成算法GBM--调参 2 scaler=StandardScaler().fit(x_train) 3 rescaledX=scaler.transform(x_train) 4 param_grid={'n_estimators':[10,50,100,200,300,400,500,600,700,800,900]} 5 model=GradientBoostingClassifier() 6 kfold=KFold(n_splits=num_folds,random_state=seed) 7 grid=GridSearchCV(estimator=model,param_grid=param_grid,scoring=scoring,cv=kfold) 8 grid_result=grid.fit(X=rescaledX,y=y_train) 9 print('最优:%s 使用%s' % (grid_result.best_score_,grid_result.best_params_))
最优:0.8614457831325302 使用{'n_estimators': 200}
确定最终模型
依据上面的测试,采用支持向量机(SVM),通过训练集数据生成算法模型,并通过预留的评估数据来评估模型。
在算法评估过程中发现,支持向量机对正太化的数据具有较高的准确度,所以对训练集做正太化处理,对评估数据集也做相同的处理。
1 #训练模型 2 scaler=StandardScaler().fit(x_train) 3 rescaledX=scaler.transform(x_train) 4 model=SVC(C=1.5,kernel='rbf') 5 model.fit(X=rescaledX,y=y_train) 6 7 #评估算法模型 8 rescaledX_validation=scaler.transform(x_validation) 9 predictions=model.predict(rescaledX_validation) 10 print(accuracy_score(y_validation,predictions)) 11 print(confusion_matrix(y_validation,predictions)) 12 print(classification_report(y_validation,predictions))
最优:0.8674698795180723 使用{'n_estimators': 500}
0.8571428571428571
[[23 4]
[ 2 13]]
precision recall f1-score support
M 0.92 0.85 0.88 27
R 0.76 0.87 0.81 15
micro avg 0.86 0.86 0.86 42
macro avg 0.84 0.86 0.85 42
weighted avg 0.86 0.86 0.86 42
以上是只采用参数优化后的SVM得到的结果,看起来比集成算法效果还好。





