B-Tree vs LSM-tree
一。已排序文件的查找时间
对一个有N笔记录的已排序表进行二叉查找,可以在O(log2N)比较级完成。如果表有1,000,000笔记录,那么定位其中一笔记录,将在20
( log21,000,000 = 19.931) 个比较级内完成。从磁盘上读取一笔记录,与之后的比较键值操作相比,在花费的运行时间上,读取操作处于支
配地位。从磁盘读取记录的时间涉及到一个寻道时间和旋转延迟。
- 读写头沿径向移动,移到要读取的扇区所在磁道的上方,这段时间称为寻道时间(seek time)
- 通过盘片的旋转,使得要读取的扇区转到读写头的下方,这段时间称为旋转延迟时间(rotational latency time)。
一个7200(转/min)的硬盘,每旋转一周所需时间为60*1000ms/7200=8.33ms,则平均旋转延迟时间为8.33÷2=4.17毫秒(平均
情况下,需要旋转半圈)。如此,在1,000,000中定位一笔记录将会话花费20*8ms=160ms。
二。提升查找的索引
在上面的例子中,初始磁盘读取从2个因素限制了查找范围。这可以通过创建一个辅助索引来改善,这个索引包含每块磁盘块上的首笔记录
(稀疏索引)。这个辅助索引可能只有原始数据库的1%大小,它可以更快速地被检索。在辅助索引中查找入口可以告诉我们在主数据库中要读
去哪一块。创建辅助索引的窍门是可以重复地给辅助索引创建辅助索引。多层次的辅助索引,使得查找问题从约为log2N 磁盘读取开销的二分
查找,变成logbN 磁盘读取开销的查找,其中b为分块入口数目(b = 100 则logb1,000,000 = 3 次读取)。在实际中,如果主数据库被频繁查找,
辅助索引可能会存储在磁盘缓存中,所以它们不会产生磁盘读取。
三。插入和删除带来的麻烦
如果数据库不会改变,那么编制索引就很简单,如果他们会改变,那么管理数据库及其索引就变得非常麻烦。从数据库中删除记录不会引
起太大问题:索引可以保持不变,记录只需要标记为已删除。数据库仍然保持有序状态。如果会有很多删除,之后查找和存储就不再那么高效了。
在一个有序文件中进行插入将是个灾难,因为需要给插入的记录制造空间。在文件中第一笔记录后插入记录需要把所有记录向后偏移一个位置。
如此的操作在实际中实在太过昂贵。
一种做法是预留一些空间给插入操作。磁盘块有一些空闲空间允许后来的插入,而不是高密度地填充。
四。B树运用的理念
B树使用了以上所有的想法。特别是:
- 保持键值有序,以顺序遍历
- 使用层次化的索引来最小化磁盘读取
- 使用不完全填充的块来加速插入和删除
- 通过优雅的遍历算法来保持索引平衡
另外,B树通过保证内部节点至少半满来最小化空间浪费。一棵B树可以处理任意数目的插入和删除。
五。什么数据结构可以作为数据库索引
考虑到range查询, 所以hash索引不行。对于关系数据库, 基本都是用B+树作为索引机制, 而没有用二叉树或他的变种红黑树的, 为什么?
一般来说,索引本身也很大,不可能全部存储在内存中,因此索引往往以文件的形式存储的磁盘上。这样的话,索引查找过程中就要产
生磁盘I/O消耗,相对于内存存取,I/O存取的消耗要高几个数量级,所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁
盘I/O操作次数
主存和磁盘以页为单位交换数据(在许多操作系统中,页得大小为4k), 页是计算机管理存储器的逻辑块, 这就意味着, 就算你只需要1byte
的数据, 每次也要读一页出来. 所以如果想要减少磁盘读取次数, 就需要合理的组织存储结构, 使每次读出的页中包含更多我们需要的信息.
可以想象在遍历索引树的时候, 如果所有的树节点都是存在磁盘上的, 那么我们需要访问节点的个数, 就是我们实际需要的磁盘I/O次数.
因为你无法保证你读出一个page里面包含你想遍历的多个节点.
对于索引树而言, 访问次数等于树高, 那么即树高越高的树型结构, 效率越低.所以对于平衡二叉树, 树高等于log2N, 明显效率太低.于是产生了B树,
B树就是增加每个节点的度, 度由2变成n, 这样树高大大降低, 一般实际只有3左右.
这个想法很自然, 我们使一个节点包含尽可能多的信息, 由2个分支到n个分支, 但是又要保证一个节点的信息必须在一个page中, 不能超出page大小.
在page大小固定的情况下, B树的度是由每个度的大小(keysize + datasize + pointsize)决定的, 当然希望B树的度尽量的大, 这样树高就
越低.这个就是B+树产生的原因, 因为在B树中节点是存放data的, 而在B+树中所以data都放到了leaf节点, 这样就是树节点的度得到了大大的
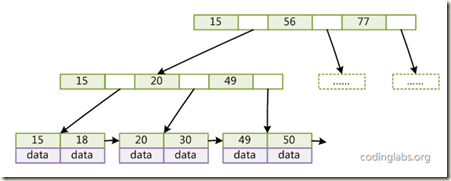
提高.而数据库实际使用的是带有顺序访问指针的B+Tree, 如图
在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针,就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能
六。如何解决高速读写
1. 尽可能快的写
对磁盘来说,最快的写入方式一定是顺序的将每一次写入都直接写入到磁盘中即可。但这样带来的问题是,我没办法查询,因为每次查询一个值
都需要遍历整个数据才能找到。 典型的例子是HDFS, 支持海量写和顺序读,不支持随机读。
2. 尽可能快的读
如果需要尽可能快的读到, 保持所有数据都是有序的,就可以很快的读到。 典型的例子就是B+树。但是需要保持全局有序, 必然会影响写的效率,
这就是B+树的问题:如果有大量的随机写, 每个写都可能需要操作不同的磁盘文件,效率很低,而且造成大量磁盘碎片,影响磁盘利用率
所以不可能同时达到读和写的快速, 最终的方案就是折衷,牺牲部分读速度, 来保证写速度。这个就是LSM-tree和SSTable的原理。