排序算法2
计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
实现步骤:
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
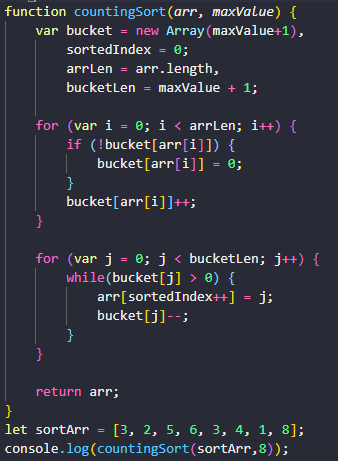
桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

function bucketSort(arr, bucketSize) { if (arr.length === 0) { return arr; } var i; var minValue = arr[0]; var maxValue = arr[0]; for (i = 1; i < arr.length; i++) { if (arr[i] < minValue) { minValue = arr[i]; // 数据的最小值 } else if (arr[i] > maxValue) { maxValue = arr[i]; // 数据的最大值 } } //桶的初始化 var DEFAULT_BUCKET_SIZE = 5; // 设置桶的默认数量为5 bucketSize = bucketSize || DEFAULT_BUCKET_SIZE; var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1; var buckets = new Array(bucketCount); for (i = 0; i < buckets.length; i++) { buckets[i] = []; } //利用映射函数将数据分配到各个桶中 for (i = 0; i < arr.length; i++) { buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]); } arr.length = 0; for (i = 0; i < buckets.length; i++) { insertionSort(buckets[i], buckets[i].length); // 对每个桶进行排序,这里使用了插入排序 for (var j = 0; j < buckets[i].length; j++) { arr.push(buckets[i][j]); } } return arr; } function insertionSort(arr, n) { if (n <= 1) { return arr; } for (var i = 1; i < n; i++) { let value = arr[i]; for (j = i - 1; j >= 0; j--) { if (arr[j] > value) { arr[j + 1] = arr[j] } else { break } } arr[j + 1] = value } return arr } let sortArr = [3, 2, 5, 6, 3, 4, 1, 8]; console.log(bucketSort(sortArr));
基数排序
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。
var counter = []; function radixSort(arr, maxDigit) { var mod = 10; var dev = 1; for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) { for(var j = 0; j < arr.length; j++) { var bucket = parseInt((arr[j] % mod) / dev); if(counter[bucket]==null) { counter[bucket] = []; } counter[bucket].push(arr[j]); } var pos = 0; for(var j = 0; j < counter.length; j++) { var value = null; if(counter[j]!=null) { while ((value = counter[j].shift()) != null) { arr[pos++] = value; } } } } return arr; }
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
- 基数排序:根据键值的每位数字来分配桶;
- 计数排序:每个桶只存储单一键值;
- 桶排序:每个桶存储一定范围的数值;
选择一个通用的、高性能的排序函数
如何选择通用排序:
- 线性排序算法(计数排序、桶排序、基数排序)的时间复杂度比较低,适用场景比较特殊,通用性不强;
- 如果对小规模数据进行排序,可以选择时间复杂度是 O(n ) 的算法;如果对大规模数据进行排序,时间复杂度是 O(nlogn) 的算法更加高效,为了兼顾任意规模数据的排序,一般首选选时间复杂度是 O(nlogn) 的排序算法(归并排序、快速排序、堆排序)来实现排序函数;
- 归并排序并不是原地排序算法,空间复杂度是O(n)。对于数据量较大的排序,可能会导致空间耗费翻倍。
- 快速排序比较适合来实现排序函数,但是,我们也知道,快速排序在最坏情况下的时间复杂度是 O(n2),如果数据原来就是有序的或者接近有序的,每次分区点都选择最后一个数据,那快速排序算法就会变得非常糟糕,时间复杂度就会退化为 O(n2)。实际上,这种 O(n2) 时间复杂度出现的主要原因还是因为我们分区点选的不够合理。


