排序算法1

常见排序算法

排序算法	时间复杂度	是否基于比较
冒泡排序、插入排序、选择排序	O(n2)	是
快速排序，归并排序	O(nlogn)	是
桶排序、计数排序、基数排序	O(n)	否

常见概念

原地排序：

原地排序算法，就是特指空间复杂度是 O(1) 的排序算法，例如冒泡排序、插入排序和选择排序都是原地排序。

稳定排序：

在排序过程中，如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

我通过一个例子来解释一下。比如我们有一组数据 2，9，3，4，8，3，按照大小排序之后就是2，3，3，4，8，9。这组数据里有两个 3。经过某种排序算法排序之后，如果两个 3 的前后顺序没有改变，那我们就把这种排序算法叫作稳定的排序算法；如果前后顺序发生变化，那对应的排序算法就叫作不稳定的排序算法。

排序算法的分析方法：

• 排序算法的执行效率
• 排序算法的内存消耗（原地排序）
• 排序算法的稳定性（稳定性）

冒泡排序

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序工作。

例如我们要对一组数据 4，5，6，3，2，1，从小到到大进行排序。第一次冒泡操作的详细过程就是这样：

  

 优化

当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。

 插入排序

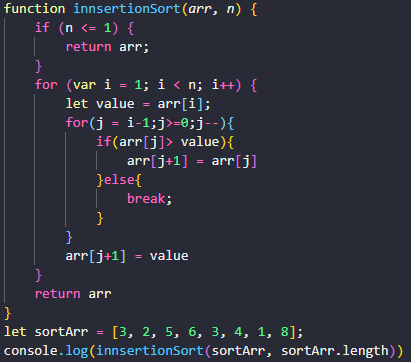
一个有序的数组，我们往里面添加一个新的数据后，如何继续保持数据有序呢？很简单，我们只要遍历数组，找到数据应该插入的位置将其插入即可。

这是一个动态排序的过程，即动态地往有序集合中添加数据，我们可以通过这种方法保持集合中的数据一直有序。而对于一组静态数据，我们也可以借鉴上面讲的插入方法，来进行排序，于是就有了插入排序算法。

    

选择排序

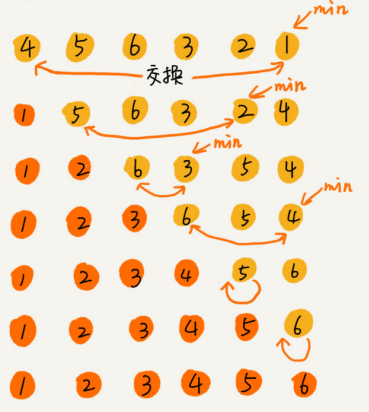
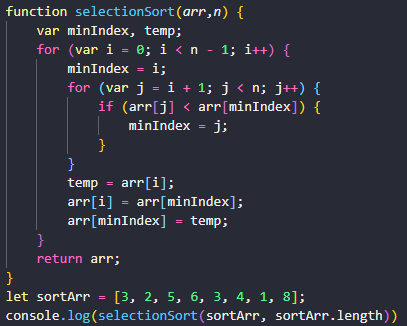
选择排序算法的实现思路有点类似插入排序，也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

   

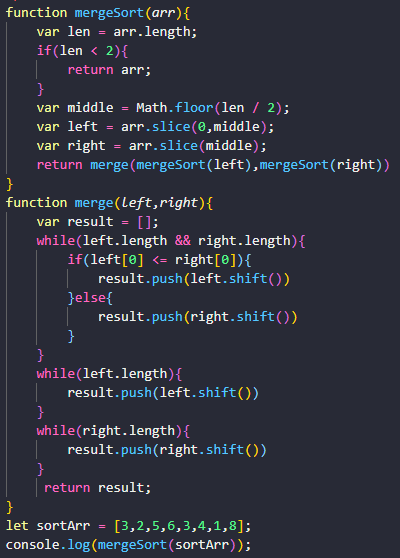
 归并排序

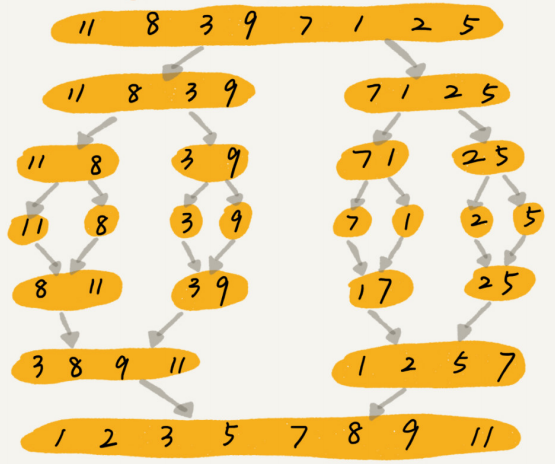
归并排序的核心思想还是蛮简单的。如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。归并排序使用的就是分治思想。分治，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。

分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧。

   

 快速排序

 快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。事实上，快速排序通常明显比其他 Ο(nlogn) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

 实现步骤：

1. 从数列中挑出一个元素，称为 "基准"（pivot）；
2.  重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

function quickSort(arr, left, right) {
            var len = arr.length,
                partitionIndex,
                left = typeof left != 'number' ? 0 : left,
                right = typeof right != 'number' ? len - 1 : right;

            if (left < right) {
                partitionIndex = partition(arr, left, right);
                quickSort(arr, left, partitionIndex - 1);
                quickSort(arr, partitionIndex + 1, right);
            }
            return arr;
        }

        function partition(arr, left, right) { // 分区操作
            var pivot = left, // 设定基准值（pivot）
                index = pivot + 1;
            for (var i = index; i <= right; i++) {
                if (arr[i] < arr[pivot]) {
                    swap(arr, i, index);
                    index++;
                }
            }
            swap(arr, pivot, index - 1);
            return index - 1;
        }

        function swap(arr, i, j) {
            var temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }

        function partition2(arr, low, high) {
            let pivot = arr[low];
            while (low < high) {
                while (low < high && arr[high] > pivot) {
                    --high;
                }
                arr[low] = arr[high];
                while (low < high && arr[low] <= pivot) {
                    ++low;
                }
                arr[high] = arr[low];
            }
            arr[low] = pivot;
            return low;
        }

        function quickSort2(arr, low, high) {
            if (low < high) {
                let pivot = partition2(arr, low, high);
                quickSort2(arr, low, pivot - 1);
                quickSort2(arr, pivot + 1, high);
            }
            return arr;
        }
        let sortArr = [3, 2, 5, 6, 3, 4, 1, 8];
        console.log(quickSort(sortArr));