最优化方法课程总结五 -- 对偶理论

对偶问题的出现

这里主要介绍约束优化问题的对偶形式，要说为什么出现对偶可能是因为原问题的对偶问题一定是凸规划。
约束优化问题的一般形式：

\[\begin{matrix} min f(x)\\ s.t. g_i(x)\geqslant 0, i=1,...,m)\\ h_j(x)=0, j=2,...,l)\\ x\in D \end{matrix} \]

该问题的对偶问题为：

\[\begin{matrix} max \theta(w,v)\\ s.t. w\geqslant 0\\ \end{matrix} \]

其中，\(\theta(w,v) = inf \begin{Bmatrix} {f(x)-\sum_{i=1}^{m}w_i g_i(x)-\sum_{j=1}^l v_jh_j(x)| x \in D} \end{Bmatrix}\)
从上述问题中可以看出可行域为凸集合，目标函数是拉格朗日函数（部分 因为有定义域的限制）Lagrange函数\(L(x;w,v)\)是\(w,v\)的线性函数，对偶函数\(\theta(w,v)\)作为线性函数的逐点下确界，必然是一个凹函数。故对偶问题一定是凸规划问题，这也是选用对偶理论的原因之一。

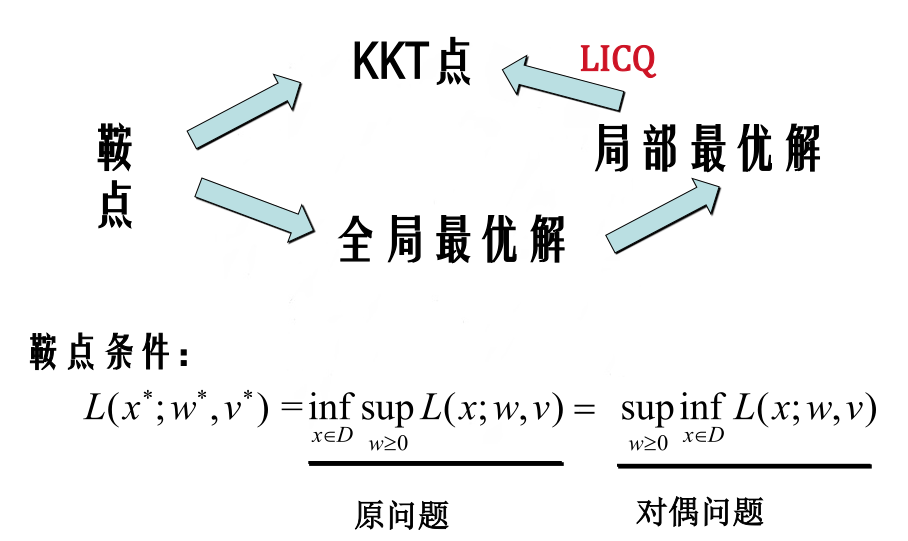
接下来对\(inf_{x \in D} sup_{w≥0}L(x;w,v)\)与\(sup_{w≥0}inf_{x \in D} L(x;w,v)\)进行讨论，这两个值是否相等呢？
答案是不一定相等，只有在两个问题都存在最优解时才相等。【一个是高的里边选矮的，一个是筷子里边拔旗杆...】

具体情况可以参见鞍点的相关知识。弱对偶定理保证原问题结果大于等于对偶问题结果，强对偶定理保证两者相等。鞍点的概念等在此不做整理。
可以利用该定理对之后介绍的对偶问题和原问题的边界进行一定的限制，当二者取值相等时，都达到了最优解。

对偶问题的目标函数

注意：线性对偶理论的全部特性都是由这个目标函数决定的！

\[\begin{matrix} \theta(w,v)\\ \\ =inf\begin{Bmatrix} c^Tx-w^T(A_1x-b_1)-v^Tx(A_2x-b_2)|x\in D \end{Bmatrix} \\ =inf\begin{Bmatrix} (c^T-w^TA_1-v^TA_2)x+w^Tb_1+v^Tb_2|x\in D \end{Bmatrix} \\ = \left\{\begin{matrix} w^Tb_1+v^Tb_2,if c^T-w^TA_1-v^TA_2\geqslant 0\\ -\infty, if c^T-w^TA_1-v^TA_2 \ngeqslant 0 \end{matrix}\right. \end{matrix} \]

对\(x\)来说，实际上是线性函数。在大于0的定义域中，斜率为正【所以是小于】才能找到最小值，同时尽可能放大截距。横竖向量变化导致转置的出现！
所以对偶问题如下：

\[\begin{matrix} max\,b_1^Tw+b_2^Tv\\ s.t.\ A_1^Tw+A_2^Tv\leqslant c \\ w\geqslant 0 \end{matrix} \]

这是一切问题的源泉（线性方面）
所以在写某线性规划问题的对偶问题时，更换目标函数的max和min，把目标函数的\(c\)和约束的\(b\)进行互换，系数矩阵的转置保证整个斜率的变化，系数的变化与不等式的符号则要看定义域，是在x的正半轴还是负半轴，由此来决定是大于还是小于。同样对偶问题中的w的正负实际上也是由原来不等式的正负。【只需要记住互补松弛符号乘起来是正的即可，还是那一句拉格朗日函数小于等于原函数\(f(x)\)】

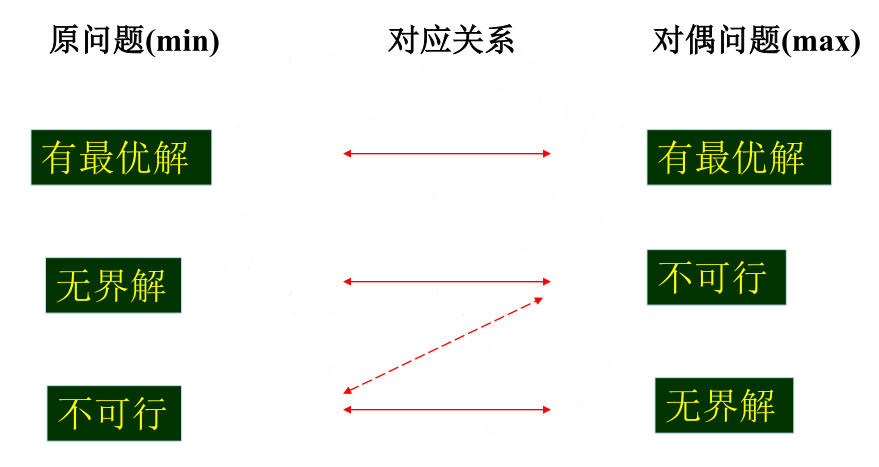
原问题与对偶问题的对应关系

【终于赶在2021年的最后一天写完60篇~~】