最优化方法课程总结三-- 最速下降法、牛顿法和线性共轭梯度法

故事继续从选定方向的选定步长讲起

首先是下降最快的方向 -- 负梯度方向衍生出来的最速下降法

最速下降法

顾名思义，选择最快下降。包含两层意思：选择下降最快的方向，在这一方向上寻找最好的步长。到达后在下一个点重复该步骤。定方向 选步长 前进...

优化问题的模型：\(min f(x)\) 其中\(f\)至少一阶连续可微
令\(g(x)=\triangledown f(x), g_k=\triangledown f(x_k)\)，则最优步长\(\alpha_k=arg min f(x_k + \alpha d_k)\)
根据链式法则和一阶最优性条件可以得到最优步长的正交性，进行求解即可。
最速下降法全局收敛，计算量与存储量小，线性收敛，不具备二次终止性

牛顿法

该方法主要应用的是泰勒展开的前三项（到二次项部分）保证其二阶导等于0。可以有以下计算公式（又被称为牛顿方程，这也是方法名字的原因）：
\(\triangledown ^ 2 f(x_k)d + \triangledown f(x_k)=0\)
牛顿方向：\(d_{k} ^ N = -[\triangledown ^2 f(x_k)]^{-1} \triangledown f(x_k)\)
牛顿步：\(x_{k+1}=x_k-G_k ^{-1}g_k\)

注意：把步长和方向和到了一起
牛顿法局部收敛（初始点需要接近最优解集合），计算量和存储量大（要求二阶导），二次收敛，具备二次终止性

线性共轭梯度法

该方法主要是将线性方程组的求解问题转化为严格凸二次规划问题。利用数值迭代方法，沿共轭方向进行线搜索（取搜索方向为当前迭代点的负梯度方向与前一迭代的搜索方向的线性组合）

在线性共轭方向法中，初始点处的搜索方向取为该点的负梯度方向。而后各共轭方向\(d_k\)由第\(k\)次迭代点\(x_k\)处的负梯度\(-g_k\)与已得的共轭向量\(d_{k-1}\)的线性组合来确定。
\(d_k=-g_k+\beta_{k-1}d_{k-1}\)
有以下计算公式：【推导过程先放一放 过段时间补上！】

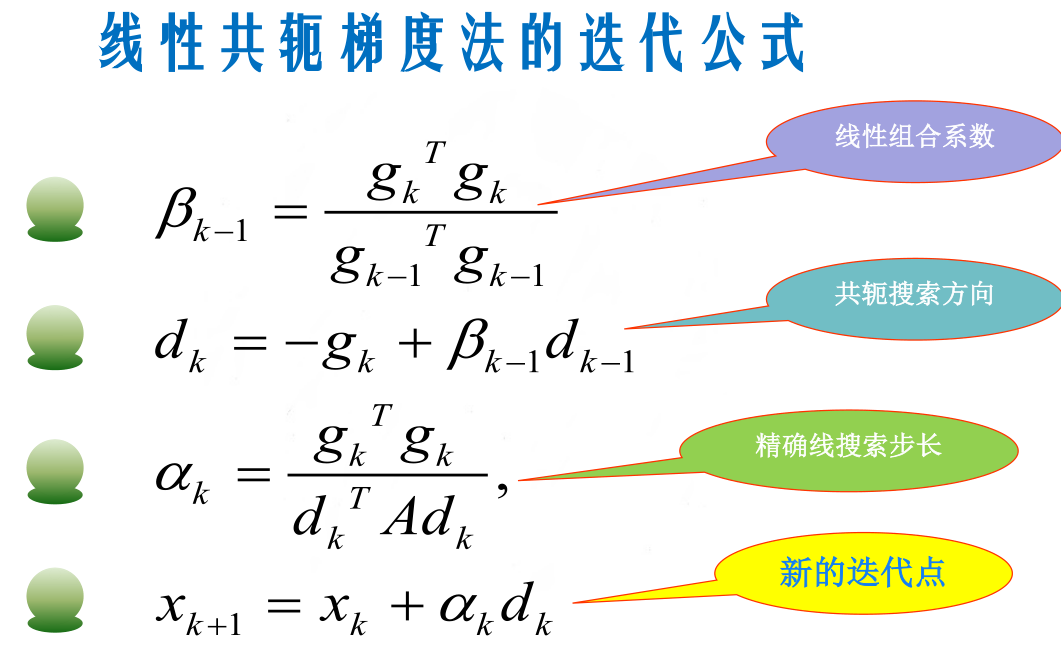
共轭梯度法初始点任意选取，计算量与存储量小，线性收敛速率，具有二次终止性。