最优化方法课程总结一 --- 凸规划与无约束规划
本篇是对自己学习《最优化方法》的一些脉络、思路的记载,也有可能会有一点点思考。
贯穿本学期课程的主要内容实际上是泰勒公式和线性系统的择一性。当然主要是因为线性情况比较好求解,且任何函数取局部都可以线性近似,解决线性问题具有一般意义。
泰勒公式
一般来讲 ,泰勒公式展开只需要用到二阶即可。其本质意义在于用多项式函数来逼近函数,求导,一阶即为切线近似。【推导原理:保证导数相等且经过这一点】
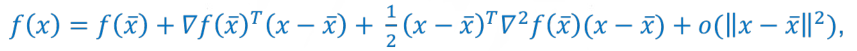
线性系统的择一性
Farkas 引理:设A为m×n矩阵,c为n维列向量,则\(Ax≤0,c^Tx>0\)有解的充要条件是\(A^Ty=c, y≥0\)无解。
Gordan定理:设A为m×n矩阵,那么\(Ax<0\)有解的充要条件是不存在非零向量\(y≥0\),使得\(A^Ty=0\)。
引理1:若系统\(Ax<0, Bx=0\)无解,则系统\(A^Ty+B^Tz=0,y≥0\),且\(y≠0\)或\(z≠0\)有解。
这三条引理贯穿线性规划问题的求解思想,只要理解了这三条,沿着这个轨迹走就很容易理解KKT条件、拉格朗日函数、单纯形法、对偶之间的思想和联系!
思考路径
-
在应用泰勒展开时,需要对其导数进行计算。首先需要判断一个函数是否一阶二阶可微和具体值。
需要求的函数千变万化,一般变化规则是:从一维函数到高维函数,普通函数到向量函数
一阶:导数(此时梯度和导数等价)
二阶:Hesse矩阵(用的是偏导数)
向量函数的一阶:Jacobi矩阵 梯度向量构成的矩阵【二阶同理,相当于对多个函数求二阶导】 -
在确定该函数可以用多项式函数逼近时,需要将考虑问题的范围不断缩小,找到性质比较好的问题进行求解,然后进行推广或近似。故有凸集的定义和性质(升缩交运算封闭)
凸集最明显的特征在于连接集合中任意两个点,线段上的点依然属于该集合。这样的特性保证了所有集合里的点可以在“同一边”,可以当成是凸集分离定理的一种形象理解。
在验证一个集合是否为凸集时可以采用上述定义验证,也可以利用凸集与凸集之交仍为凸集通过一些比较明显的凸集进行判断(常用的凸集有:超平面、半空间和射线等) -
在刻画凸集时,一般需要点和方向。这催生了极点和极方向的概念。在方向的问题探讨上,涉及到了一点一方向即锥(射线 正向伸缩);
方向:沿着这个向量的方向走,所有的点都在集合内。【有限集无方向】
极方向:其它方向表示不出来的方向(可理解为最边上那个方向)
极点:不存在两个点的连线经过这个点(可理解为边界交点)通过极点和极方向就可以对凸集进行刻画。
有限个半空间的交是多面集;极点、极方向(边界方向,不能被表出) -
集合加上对应映射就是函数,所以之后介绍凸函数的判别方法:
· 定义式(被切线托起来,线性逼近的值小于函数真值)\(f(x)≥f(y)+f'(y)(x-y)+...\)
· 最优性条件:凸函数,一阶导为0,则为最小值点。
· 二阶判别条件:在\(x\)处的Hesse矩阵是半正定的(二阶可微函数),若为正定则\(f(x)\)为严格凸函数。
这三条判别条件的主要思想在于切线托起曲线,函数值大于切线值,即泰勒公式左边减右边需为正。 -
根据凸函数的水平集性质,在凸集上找凸函数的最优解一定能找到。
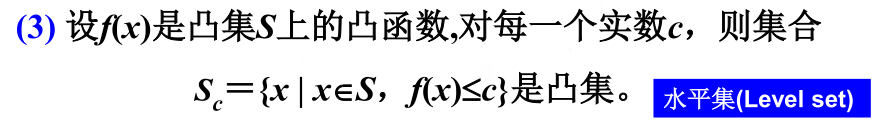
也就衍生了凸规划的定义:

凸规划的性质:
· 凸规划问题的任一局部最优解为全局最优解
· 凸规划问题的解集为凸集
· 严格凸规划问题若存在最优解,则最优解唯一。【严格凸规划并不一定存在最优解】
· 凸规划问题的全局最优解与稳定点等价
· 凸规划问题的KKT点为其全局最优解
由此,问题结构搭建基本完毕,接下来主要解决如何找到凸函数的最小值问题。先从最简单的无约束优化问题切入。
-
无约束优化最优性条件
主要思想是局部不动达到稳定,可认为达到了局部最优解。在凸函数这种极好的性质下,局部最优就是全局最优。带上泰勒公式理解即可。
寻找最值的搜索给定步长和方向判断趋势直到梯度为可认为找到了局部最优解(若为凸函数则是全局最优解)
· 局部最优解的一阶必要条件:若是局部最优解,则一阶导为0(反之 导数为0不一定是局部最优解;必要条件的意思是 必须要满足才有可能成立,但满足也不一定成立)
· 局部最优解的二阶必要条件:若是局部最优解,则二阶导为0,Hesse矩阵半正定。
· 二阶充分条件:若一阶导为0,二阶导正定,则是严格局部最优解。若二阶导为半正定,则是局部最优解。
· 无约束规划充要的最优性条件:一阶导为0 -
对最小二乘问题和正则化策略的理解。

