Leetcode刷题记录--1277. 统计全为 1 的正方形子矩阵

前言：这题的规律性挺强的，没怎么费力气就找出来了，增强信心hhh

示例 1：

输入：matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出：15
解释：
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.

这道题也是一道线性规划题，我现在做的线性规划题还不算多，一般看到一道题，就会思考怎么拆分成子问题，怎么找规律。

如果我们需要找一个矩阵所形成的正方形，首先我们需要找边长为1的正方形，这个很好说，只要matrx[i][j]=1,那么这就是一个边长为1的正方形
接下来我们考虑边长为2的正方形，仔细观察可以发现，如果i或者j为0，也就是处于第一行或者第一列，其实是可以直接打入冷宫的，显然这个时候它所能形成的正方形最大也只能是边长为1
但是以上只是边长为1和为2的情况，其他怎么办呢，怎么才能把之前算过的结果用上呢？
仔细考虑，有如下重复之处：

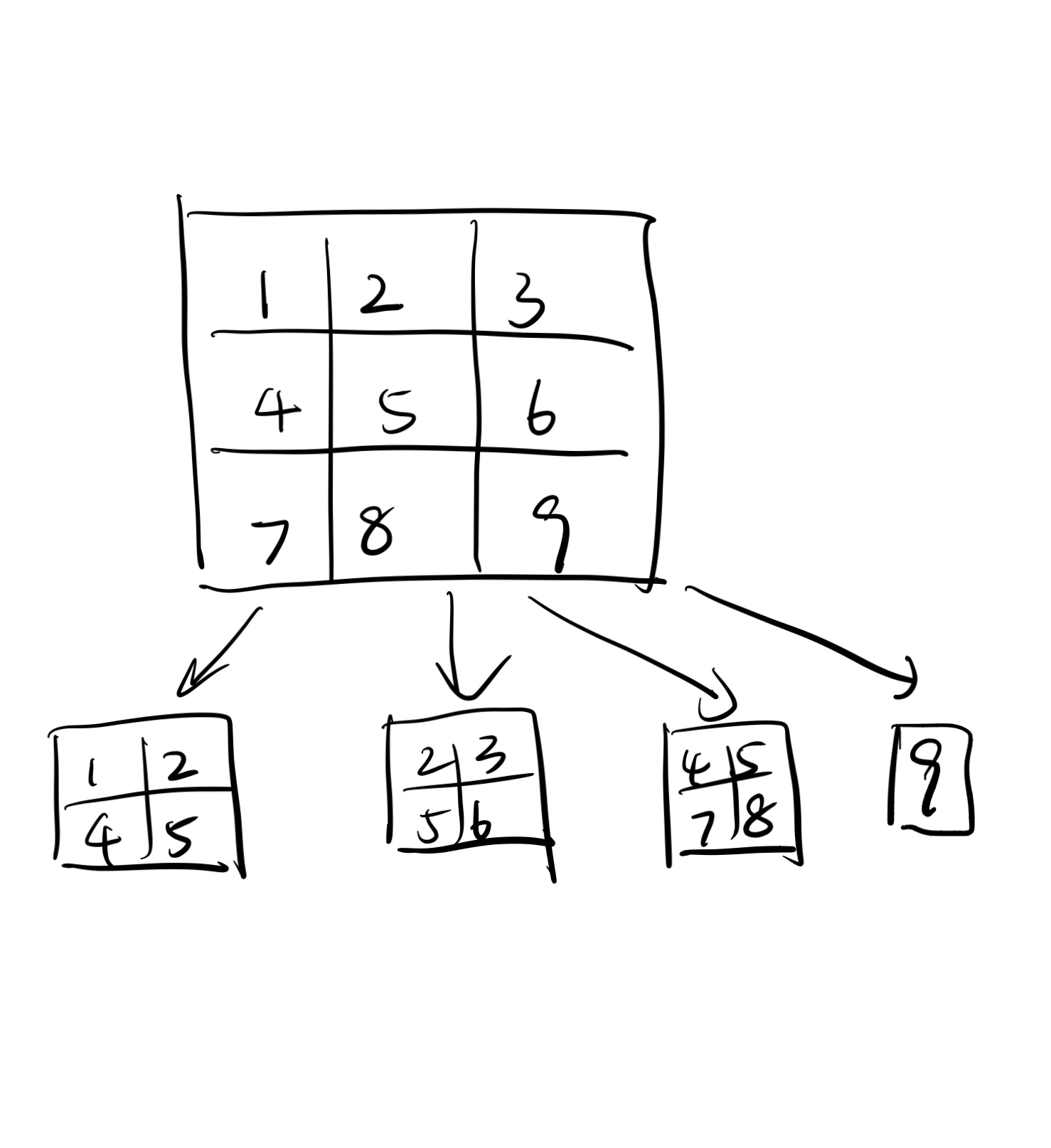
对于一个边长为3的正方形，它是可以由3个边长为2的正方形外加当前那一个点覆盖，也就是说我们不需要去逐一计算9个点。（这个是不是有点像最原始的方式：滑动遍历图像以寻找像中目标）

我们开一个相同size的dp二维数组用来存放已知结果，其中每一个元素代表以它右下角元素的正方形个数，结合上面的推论，我们只需要考虑matrix[i][j]、dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]

\[dp[i][j]= \begin{cases} matrix[i][j] & min(i,j) < 1 || matrix[i][j]==0\\ matrix[i][j] + dp[i][j-1] + dp[i-1][j] + dp[i-1][j-1]& min(i,j) >= 1 \end{cases}\]

故有具体实现如下：

class Solution {
public:
    int countSquares(vector<vector<int>>& matrix) {
        int m = matrix.size();
        if(m == 0){
            return 0;
        }
        int n = matrix[0].size();
        int minh, sum=0;
        int dp[m][n];
        for(int i = 0; i < m; i++){
            
            for(int j = 0; j < n; j++){
                minh = min(i,j); 
                if(minh < 1 || matrix[i][j] ==0){
                    dp[i][j] = matrix[i][j];
                }else{
                    minh--;
                    //比较dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]
                    dp[i][j] = min(dp[i-1][j],min(dp[i][j-1],dp[i-1][j-1])) + matrix[i][j];

                }
                // cout << dp[i][j];
                sum += dp[i][j];
            }
        //    cout << endl;
        }

        
        return sum;
    }
};