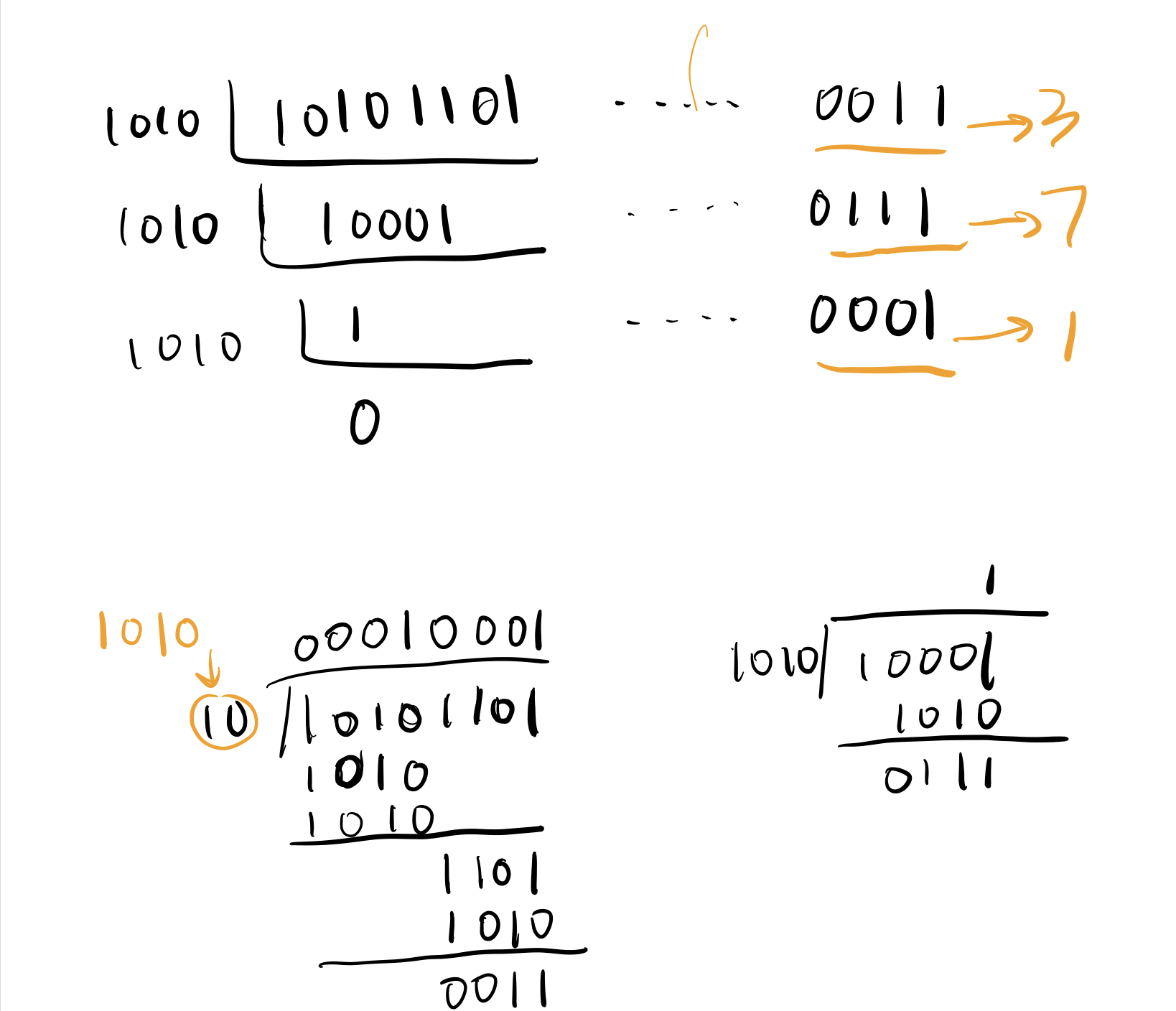
c++实现大数进制转换 （字符串模拟数字运算）

注：这个主要用于10进制及以下的相互转换

进制转换的实现与取余和取模相关：以十进制数173转换为二进制10101101为例

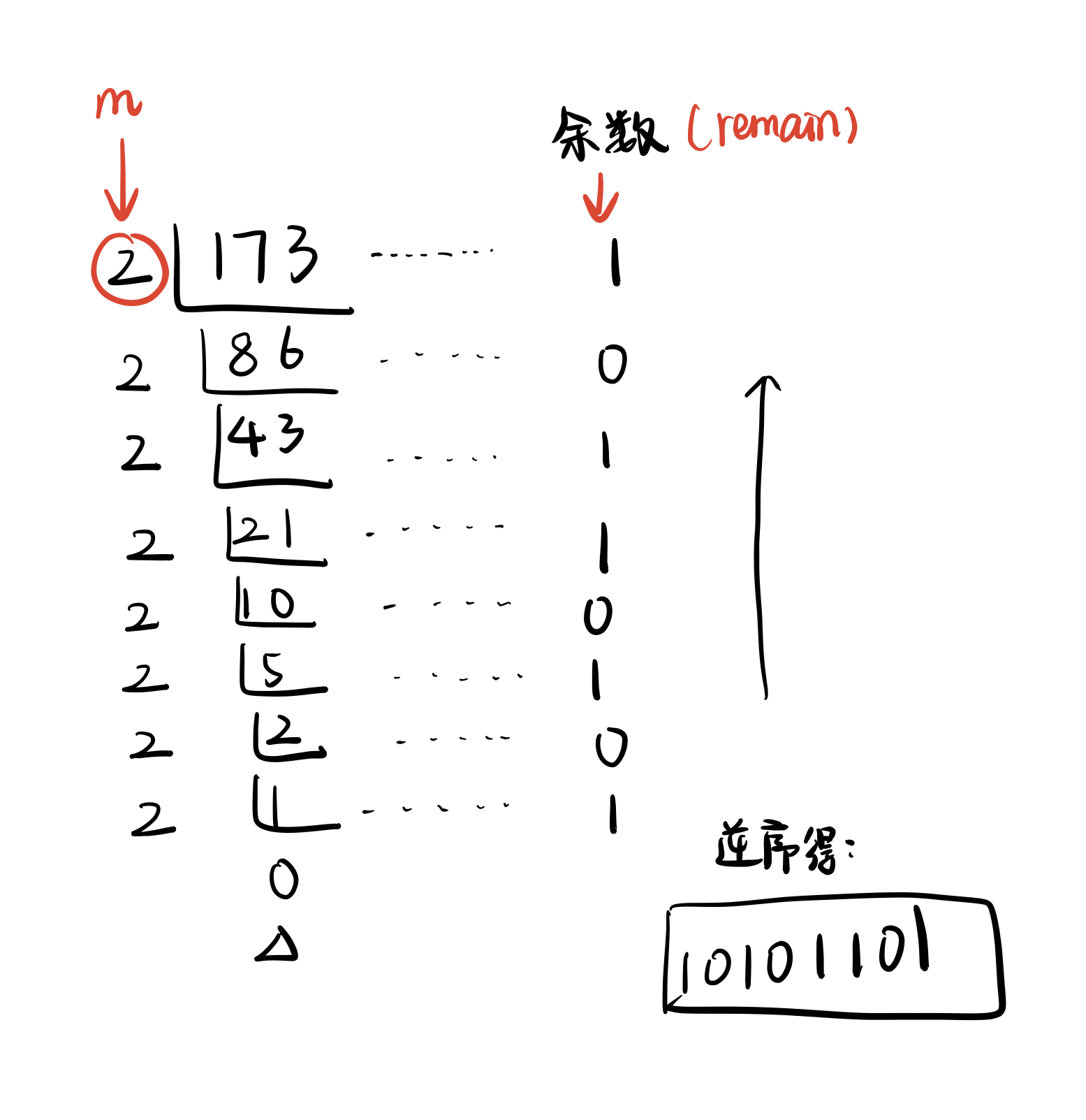
我们可以看到转换进制的具体流程就是对输入的数对2取模得到1，再对其对2整除得到下一个待处理数，直到待处理的数变成0，便将刚才得到的余数逆序输出。
那么观察一下这里的2，其实就是二进制的基数2

看完这张图，我们的脑海里应该有了大体结构，就是我们的程序输入基数，输入待处理的数字173，然后通过一个循环结构得到余数，和下一个待处理的数，循环终止的条件应该和0相关，最后再通过拼接字符串或者其他方式输出我们的余数。

那么我们还没有解决如何得到余数的问题，同样以173除2为例

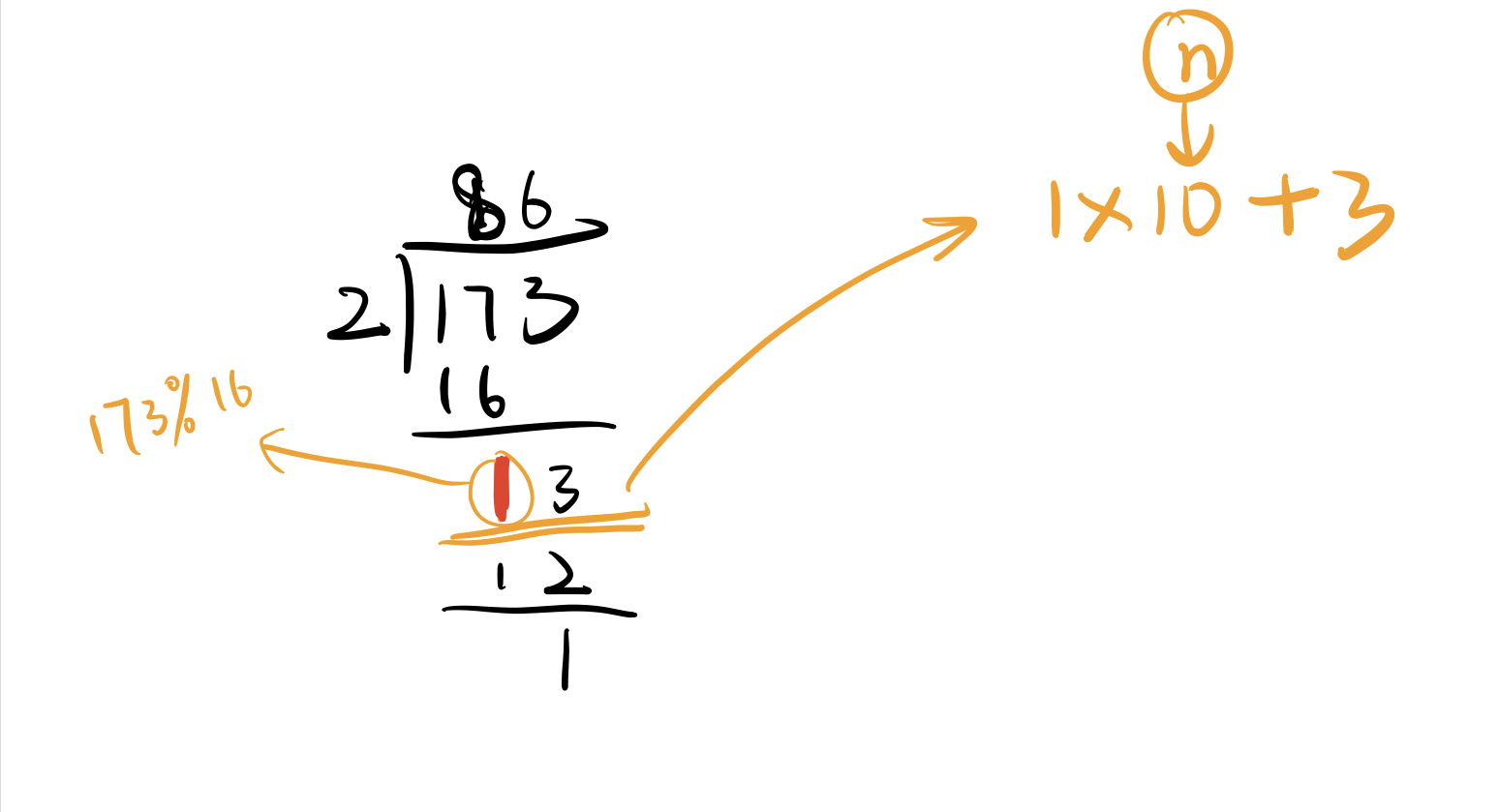
实现字符串的数字运算，其实和我们运算的过程一样，从字符串第一位开始取每一位除以m，那么如果遇到有余数的怎么处理呢？在这里17除2余1，可以发现下一步是13除2，因此余数参与下一次运算的方式应该是1*10+str[i]，str[i]是字符串的下一位，而10其实就取决于我们原来输入数字的基数，这里是十进制。那么173%2的结果是多少呢，其实就是最后一步运算得到的余数1。

具体实现代码如下：

#include<iostream>
#include<string>
#include <algorithm>
using namespace std;

string division(string str, int m, int n, int & remain){
    string result = "";
    int a;
    remain = 0;

    for(int i = 0; i < str.size(); i++){
        a = (n * remain + (str[i] - '0'));
        str[i] = a / m + '0';
        remain = a % m;
    }
    //去掉多余的0 比如10/2=05
    int pos = 0;
    while(str[pos] == '0'){
        pos++;
    }
    return str.substr(pos);
}

string conversion(string str, int m, int n){
    string result = "";
    char c;
    int a;
    //因为去掉了多余的0，所以终止条件是字符串为空 例：当上一步运算结果为"0"时，实际上返回的结果为""
    while(str.size() != 0){
        str = division(str, m , n,a);
        result = char(a + '0') +result;

    }
    return result;
}
int main(){
    string a,b;
  //  cout << division("173",2, 10);
  //  cout << conversion("10101101", 10, 2);
    cin >> a;
    b = conversion(a,2,10);

    reverse(b.begin(), b.end());
    a = conversion(b,10,2);
    cout << a << endl;


}

其实别看十进制转二进制如此，二进制转十进制也是一样的（尽管平时为了计算方便都是加法）

为了计算方便，这里的所有数字都用二进制表示