点到圆弧的距离(csu1503)+几何

1503: 点到圆弧的距离

Time Limit: 1 Sec  Memory Limit: 128 MB  Special Judge
Submit: 325  Solved: 70
[Submit][Status][Web Board]

Description

输入一个点P和一条圆弧（圆周的一部分），你的任务是计算P到圆弧的最短距离。换句话说，你需要在圆弧上找一个点，到P点的距离最小。
提示：请尽量使用精确算法。相比之下，近似算法更难通过本题的数据。

 

Input

输入包含最多10000组数据。每组数据包含8个整数x1, y1, x2, y2, x3, y3, xp, yp。圆弧的起点是A(x1,y1)，经过点B(x2,y2)，结束位置是C(x3,y3)。点P的位置是 (xp,yp)。输入保证A, B, C各不相同且不会共线。上述所有点的坐标绝对值不超过20。

 

Output

对于每组数据，输出测试点编号和P到圆弧的距离，保留三位小数。你的输出和标准输出之间最多能有0.001的误差。

 

Sample Input

0 0 1 1 2 0 1 -1
3 4 0 5 -3 4 0 1

Sample Output

Case 1: 1.414
Case 2: 4.000

HINT

 

Source

湖南省第十届大学生计算机程序设计竞赛

 
思路：根据三点确定圆心和半径；关键是确定扇形区域（尤其是优弧）
 
 
 
 
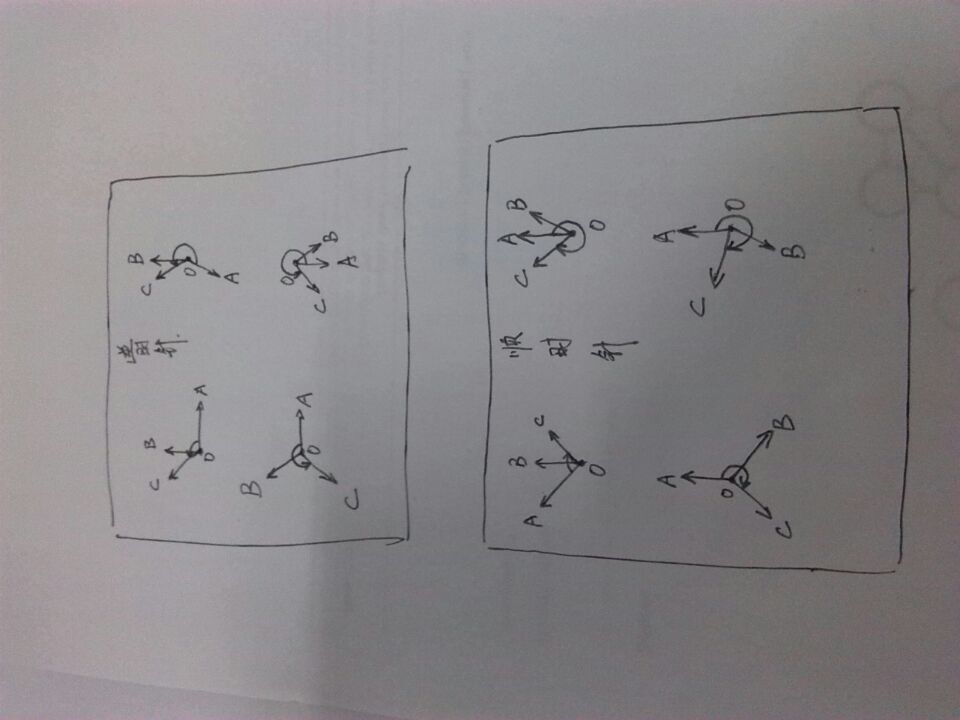
确定点在扇形区域就分两种情况，在圆内和圆外；不在扇形区域就是min(到A，到C)距离最短的；
 
 
转载请注明出处：寻找&星空の孩子 
 
题目链接：http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1503#userconsent#
 
具体见代码：
 
  1 #include<stdio.h>
  2 #include<math.h>
  3 #define PI acos(-1.0)
  4 #include<algorithm>
  5 using namespace std;
  6 struct Point
  7 {
  8     double x;
  9     double y;
 10     Point(double x=0,double y=0):x(x),y(y) {} //构造函数，方便代码编写
 11 } pt;
 12 struct Traingle
 13 {
 14     struct Point p[3];
 15 } Tr;
 16 struct Circle
 17 {
 18     struct Point center;
 19     double r;
 20 } ans;
 21 //计算两点距离
 22 double Dis(struct Point p, struct Point q)
 23 {
 24     double dx=p.x-q.x;
 25     double dy=p.y-q.y;
 26     return sqrt(dx*dx+dy*dy);
 27 }
 28 //计算三角形面积
 29 double Area(struct Traingle ct)
 30 {
 31     return fabs((ct.p[1].x-ct.p[0].x)*(ct.p[2].y-ct.p[0].y)-(ct.p[2].x-ct.p[0].x)*(ct.p[1].y-ct.p[0].y))/2.0;
 32 }
 33 //求三角形的外接圆，返回圆心和半径(存在结构体"圆"中)
 34 struct Circle CircumCircle(struct Traingle t)
 35 {
 36     struct Circle tmp;
 37     double a, b, c, c1, c2;
 38     double xA, yA, xB, yB, xC, yC;
 39     a = Dis(t.p[0], t.p[1]);
 40     b = Dis(t.p[1], t.p[2]);
 41     c = Dis(t.p[2], t.p[0]);
 42 //根据 S = a * b * c / R / 4;求半径 R
 43     tmp.r = (a*b*c)/(Area(t)*4.0);
 44     xA = t.p[0].x;
 45     yA = t.p[0].y;
 46     xB = t.p[1].x;
 47     yB = t.p[1].y;
 48     xC = t.p[2].x;
 49     yC = t.p[2].y;
 50     c1 = (xA*xA+yA*yA - xB*xB-yB*yB) / 2;
 51     c2 = (xA*xA+yA*yA - xC*xC-yC*yC) / 2;
 52     tmp.center.x = (c1*(yA - yC)-c2*(yA - yB)) / ((xA - xB)*(yA - yC)-(xA - xC)*(yA - yB));
 53     tmp.center.y = (c1*(xA - xC)-c2*(xA - xB)) / ((yA - yB)*(xA - xC)-(yA - yC)*(xA - xB));
 54     return tmp;
 55 }
 56 
 57 typedef Point Vector;
 58 
 59 
 60 Vector operator + (Vector A,Vector B)
 61 {
 62     return Vector(A.x+B.x,A.y+B.y);
 63 }
 64 
 65 
 66 Vector operator - (Point A,Point B)
 67 {
 68     return Vector(A.x-B.x,A.y-B.y);
 69 }
 70 
 71 
 72 Vector operator * (Vector A,double p)
 73 {
 74     return Vector(A.x*p,A.y*p);
 75 }
 76 
 77 
 78 Vector operator / (Vector A,double p)
 79 {
 80     return Vector(A.x/p,A.y/p);
 81 }
 82 
 83 
 84 bool operator < (const Point& a,const Point& b)
 85 {
 86     return a.x<b.x||(a.x==b.x && a.y<b.y);
 87 }
 88 
 89 
 90 const double eps = 1e-10;
 91 
 92 int dcmp(double x)
 93 {
 94     if(fabs(x)<eps)return 0;
 95     else return x < 0 ? -1 : 1;
 96 }
 97 bool operator == (const Point& a,const Point& b)
 98 {
 99     return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
100 }
101 
102 double Dot(Vector A,Vector B)
103 {
104     return A.x*B.x+A.y*B.y;
105 }
106 double length(Vector A)
107 {
108     return sqrt(Dot(A,A));
109 }
110 double Angle(Vector A,Vector B)
111 {
112     return acos(Dot(A,B)/length(A)/length(B));
113 }
114 
115 
116 double Cross(Vector A,Vector B)
117 {
118     return A.x*B.y-B.x*A.y;
119 }
120 double Area2(Point A,Point B,Point C)
121 {
122     return Cross(B-A,C-A);
123 }
124 double len;
125 
126 int main()
127 {
128     int ca=1;
129     while(scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&Tr.p[0].x,&Tr.p[0].y,&Tr.p[1].x,&Tr.p[1].y,&Tr.p[2].x,&Tr.p[2].y,&pt.x,&pt.y)!=EOF)
130     {
131         //      printf("%lf %lf\n%lf %lf\n%lf %lf\n%lf %lf\n",Tr.p[0].x,Tr.p[0].y,Tr.p[1].x,Tr.p[1].y,Tr.p[2].x,Tr.p[2].y,pt.x,pt.y);
132         Circle CC=CircumCircle(Tr);
133         //      printf("%lf %lf,r=%lf",CC.center.x,CC.center.y,CC.r);
134         Point A(Tr.p[0].x,Tr.p[0].y),O(CC.center.x,CC.center.y),C(Tr.p[2].x,Tr.p[2].y),D(pt.x,pt.y),B(Tr.p[1].x,Tr.p[1].y);
135 
136         Vector OA(A-O),OB(B-O),OC(C-O),OD(D-O);
137         if(Cross(OA,OB)<=0&&Cross(OB,OC)<=0||Cross(OA,OB)>=0&&Cross(OB,OC)<0&&Cross(OA,OC)>0||Cross(OA,OB)<0&&Cross(OB,OC)>=0&&Cross(OA,OC)>0)//顺
138         {
139             if(Cross(OA,OD)<=0&&Cross(OD,OC)<=0||Cross(OA,OD)>=0&&Cross(OD,OC)<0&&Cross(OA,OC)>0||Cross(OA,OD)<0&&Cross(OD,OC)>=0&&Cross(OA,OC)>0)
140             {
141                 len=fabs(length(D-O));
142                 if(len<=CC.r) len=CC.r-len;
143                 else len=len-CC.r;
144             }
145             else
146             {
147                 len=min(fabs(length(A-D)),fabs(length(C-D)));
148             }
149         }
150         else if(Cross(OA,OB)>=0&&Cross(OB,OC)>=0||Cross(OA,OB)>0&&Cross(OB,OC)<=0&&Cross(OA,OC)<0||Cross(OA,OB)<=0&&Cross(OB,OC)>0&&Cross(OA,OC)<0)//逆
151         {
152             if(Cross(OA,OD)>=0&&Cross(OD,OC)>=0||Cross(OA,OD)>0&&Cross(OD,OC)<=0&&Cross(OA,OC)<0||Cross(OA,OD)<=0&&Cross(OD,OC)>0&&Cross(OA,OC)<0)
153             {
154                 len=fabs(length(D-O));
155                 if(len<=CC.r) len=CC.r-len;
156                 else len=len-CC.r;
157             }
158             else
159             {
160                 len=min(fabs(length(A-D)),fabs(length(C-D)));
161             }
162         }
163 
164         printf("Case %d: %0.3f\n",ca++,len);
165     }
166     return 0;
167 }
168 /*
169 0 0 1 1 2 0 1 -1
170 3 4 0 5 -3 4 0 1
171 0 0 1 1 1 -1 0 -1
172 */

 

 
posted @ 2015-07-30 22:22  寻找&星空の孩子  阅读(1161)  评论(0)  编辑  收藏  举报