Codeforces Round #304 (Div. 2) -----CF546

 

A. Soldier and Bananas

 

A soldier wants to buy w bananas in the shop. He has to pay k dollars for the first banana, 2k dollars for the second one and so on (in other words, he has to pay i·k dollars for the i-th banana).

He has n dollars. How many dollars does he have to borrow from his friend soldier to buy w bananas?

Input

The first line contains three positive integers k, n, w (1  ≤  k, w  ≤  1000, 0 ≤ n ≤ 109), the cost of the first banana, initial number of dollars the soldier has and number of bananas he wants.

Output

Output one integer — the amount of dollars that the soldier must borrow from his friend. If he doesn't have to borrow money, output 0.

Sample test(s)

input

3 17 4

output

13

 

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

#define LL __int64
LL n,k,w;

int main()
{
    int i;
    LL sum = 0;
    scanf("%I64d%I64d%I64d",&k,&n,&w);
    for(i = 1;i<=w;i++)
        sum +=i*k;
        if(n>=sum)
            printf("0\n");
        else
    printf("%I64d\n",sum-n);

    return 0;
}

 

 

B. Soldier and Badges

 

Colonel has n badges. He wants to give one badge to every of his n soldiers. Each badge has a coolness factor, which shows how much it's owner reached. Coolness factor can be increased by one for the cost of one coin.

For every pair of soldiers one of them should get a badge with strictly higher factor than the second one. Exact values of their factors aren't important, they just need to have distinct factors.

Colonel knows, which soldier is supposed to get which badge initially, but there is a problem. Some of badges may have the same factor of coolness. Help him and calculate how much money has to be paid for making all badges have different factors of coolness.

Input

First line of input consists of one integer n (1 ≤ n ≤ 3000).

Next line consists of n integers ai (1 ≤ ai ≤ n), which stand for coolness factor of each badge.

Output

Output single integer — minimum amount of coins the colonel has to pay.

Sample test(s)

input

4
1 3 1 4

output

1

input

5
1 2 3 2 5

output

2

Note

In first sample test we can increase factor of first badge by 1.

In second sample test we can increase factors of the second and the third badge by 1.

 

题意：给你n堆价值，要求得到每堆价值是独一无二的，问你往每堆加多少，最少加多少。

思路：（贪心）先排序，然后以第一个为基准，后面的不大于前面的，就加加；

转载请注明出处：寻找&星空の孩子

题目链接：http://codeforces.com/contest/546/problem/B

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <bitset>
#include <list>
#include <algorithm>
#include <climits>
using namespace std;

#define lson 2*i
#define rson 2*i+1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 5000005
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define lowbit(x) (x&-x)
const int mod = 1e9+7;
#define LL __int64
int n,a[3005];
int main()
{
    int i,j,ans;
    while(~scanf("%d",&n))
    {
        ans = 0;
        int sum1 = 0,sum2 = 0;
        for(i = 1; i<=n; i++)
        {
            scanf("%d",&a[i]);
            sum1+=a[i];
        }
        sort(a+1,a+1+n);
        sum2 = a[1];
        for(i = 2; i<=n; i++)
        {
            if(a[i] == a[i-1])
                a[i]++;
            else if(a[i]<a[i-1])
                a[i] +=(a[i-1]-a[i])+1;
            sum2+=a[i];
        }
        printf("%d\n",sum2-sum1);
    }

    return 0;
}

 

C. Soldier and Cards

 

Two bored soldiers are playing card war. Their card deck consists of exactly n cards, numbered from 1 to n, all values are different. They divide cards between them in some manner, it's possible that they have different number of cards. Then they play a "war"-like card game.

The rules are following. On each turn a fight happens. Each of them picks card from the top of his stack and puts on the table. The one whose card value is bigger wins this fight and takes both cards from the table to the bottom of his stack. More precisely, he first takes his opponent's card and puts to the bottom of his stack, and then he puts his card to the bottom of his stack. If after some turn one of the player's stack becomes empty, he loses and the other one wins.

You have to calculate how many fights will happen and who will win the game, or state that game won't end.

Input

First line contains a single integer n (2 ≤ n ≤ 10), the number of cards.

Second line contains integer k1 (1 ≤ k1 ≤ n - 1), the number of the first soldier's cards. Then follow k1 integers that are the values on the first soldier's cards, from top to bottom of his stack.

Third line contains integer k2 (k1 + k2 = n), the number of the second soldier's cards. Then follow k2 integers that are the values on the second soldier's cards, from top to bottom of his stack.

All card values are different.

Output

If somebody wins in this game, print 2 integers where the first one stands for the number of fights before end of game and the second one is 1 or 2 showing which player has won.

If the game won't end and will continue forever output  - 1.

Sample test(s)

input

4
2 1 3
2 4 2

output

6 2

input

3
1 2
2 1 3

output

-1

Note

First sample:

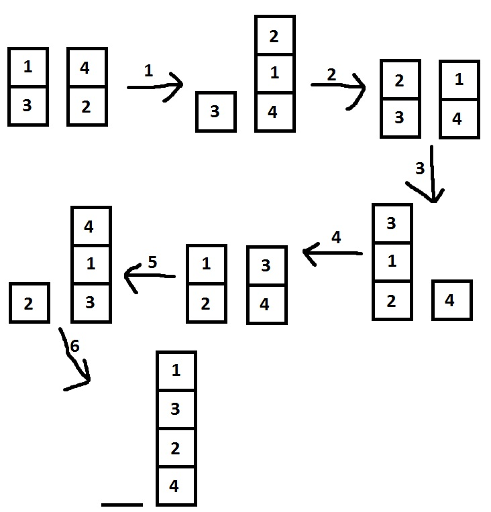
Second sample:

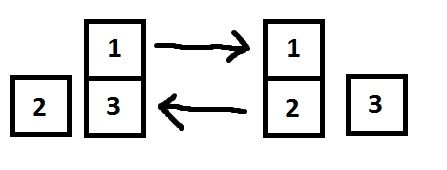
题意：给一个n（<=10）表示两人手中共有n张牌，接下来一行表示第1个人有k1张牌，k1 v1[1] v1[2]......v1[k1], v1[i]表示第i 张牌的大小，第三行表示第2个人有k2张牌，k2 v2[1] v2[2]......v2[k2], v2[i]表示第i 张牌的大小。每一轮，两人从牌顶部各出一张，谁出的牌大则两张牌归谁，放入到自己牌的底部，直到其中一个人手中没有牌出，则那个人输了。问需要多少轮，哪个人赢了。如果没有解则输出-1.

思路：（模拟题）直接模拟一下过程，主要是标记一下两个人手中牌的状态，用map<string,map<string,bool> >vist 标记一下。

转载请注明出处：寻找&星空の孩子   

题目链接：http://codeforces.com/contest/546/problem/C

 

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <bitset>
#include <list>
#include <algorithm>
#include <climits>
using namespace std;

#define lson 2*i
#define rson 2*i+1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 5000005
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define lowbit(x) (x&-x)
const int mod = 1e9+7;

map<string,map<string,int> > vis;
int n;
int k1,k2;
int a[15],b[15],c[15];
char s1[15],s2[15];

int main()
{
    int i,j,k;
    scanf("%d",&n);
    scanf("%d",&k1);
    for(i = 0; i<k1; i++)
    {
        scanf("%d",&a[i]);
        c[i] = a[i];
    }
    scanf("%d",&k2);
    for(i = 0; i<k2; i++)
    {
        scanf("%d",&b[i]);
        c[k1+i] = b[i];
    }
    sort(c,c+k1+k2);
    for(i = 0; i<k1; i++)
    {
        for(j = 0; j<k1+k2; j++)
        {
            if(a[i]==c[j])
                s1[i] = j+'0';
        }
    }
    s1[k1] = '\0';
    for(i = 0; i<k2; i++)
    {
        for(j = 0; j<k1+k2; j++)
        {
            if(b[i]==c[j])
                s2[i] = j+'0';
        }
    }
    s2[k2] = '\0';
    vis[s1][s2] = 1;
    int ans = 0;
    while(k1&&k2)
    {
        int p1 = s1[0],p2 = s2[0];
      //  printf("[%d %d %d %d]\n",p1,p2,k1,k2);

        /* printf("(1):");
         for(i = 0; i<k1; i++)
             printf("%c ",s1[i]);
         printf("\n");
         printf("(2):");
         for(i = 0; i<k2; i++)
             printf("%c ",s2[i]);
         printf("\n");*/
        if(p1>p2)
        {
            for(i = 0; i<k2; i++)
                s2[i] = s2[i+1];
            k2--;
            for(i = 0; i<k1; i++)
                s1[i] = s1[i+1];
            s1[k1-1] = p2;
            s1[k1] = p1;
            k1++;
            s2[k2] = s1[k1] = '\0';
        }
        else
        {
            for(i = 0; i<k1; i++)
                s1[i] = s1[i+1];
            k1--;
            for(i = 0; i<k2; i++)
                s2[i] = s2[i+1];
            s2[k2-1] = p1;
            s2[k2] = p2;
            k2++;
            s2[k2] = s1[k1] = '\0';
        }
     /*   printf("(1):");
        for(i = 0; i<k1; i++)
            printf("%c ",s1[i]);
        printf("\n");
        printf("(2):");
        for(i = 0; i<k2; i++)
            printf("%c ",s2[i]);
        printf("\n");*/
        if(vis[s1][s2])
        {
            ans = -1;
            break;
        }
        //printf("%d %d\n",k1,k2);
        ans++;
        vis[s1][s2] = 1;
    }
    printf("%d",ans);
    if(ans!=-1)
    {
        if(k1)
            printf(" 1");
        else
            printf(" 2");
    }
    printf("\n");

    return 0;
}

 

 

 

D. Soldier and Number Game

 

Two soldiers are playing a game. At the beginning first of them chooses a positive integer n and gives it to the second soldier. Then the second one tries to make maximum possible number of rounds. Each round consists of choosing a positive integer x > 1, such that n is divisible by x and replacing n with n / x. When n becomes equal to 1 and there is no more possible valid moves the game is over and the score of the second soldier is equal to the number of rounds he performed.

To make the game more interesting, first soldier chooses n of form a! / b! for some positive integer a and b (a ≥ b). Here by k! we denote the factorial of k that is defined as a product of all positive integers not large than k.

What is the maximum possible score of the second soldier?

Input

First line of input consists of single integer t (1 ≤ t ≤ 1 000 000) denoting number of games soldiers play.

Then follow t lines, each contains pair of integers a and b (1 ≤ b ≤ a ≤ 5 000 000) defining the value of n for a game.

Output

For each game output a maximum score that the second soldier can get.

Sample test(s)

input

2
3 1
6 3

output

2
5

 

题意：n=a！/b！问你n的素数因子的个数。

思路：素数打表；

转载请注明出处：寻找&星空の孩子

题目链接：http://codeforces.com/contest/546/problem/D

 

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <bitset>
#include <list>
#include <algorithm>
#include <climits>
using namespace std;

#define lson 2*i
#define rson 2*i+1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 5000005
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define lowbit(x) (x&-x)
const int mod = 1e9+7;
int p[N];
int a[N];
int prime[700];
LL sum[N];
void init()
{

    for(int i=0; i<700; ++i)
        prime[i] = INF;
    prime[0] = 2;
    int num = 0;
    for(int i=3; i<5005; ++i)
    {
        int x = 0;
        while(i%prime[x] && prime[x] <= i)   ++x;
        if( !(i%prime[x]) )
            a[i] = prime[x];
        else
        {
            prime[++num] = i;
            a[i] = i;
        }
    }
    a[2] =2;
    for(int i=5005; i< N; ++i)
    {
        int x = 0;
        while(i%prime[x] && prime[x] <= i)   ++x;
        if( !(i%prime[x]) )
            a[i] = prime[x];
        else
            a[i] = i;
    }
    p[2] = 1;
    for(int i=3; i <N; ++i)
        p[i] = p[i/a[i]] + 1;
}
int main()
{
    int i,j,k;
    init();
    sum[1] = 0;
   // printf("%d\n",p[4]);
    for(i = 2; i<=5000000; i++)
    {
        sum[i] = sum[i-1]+p[i];
      //  printf("%d %I64d\n",i,sum[i]);
    }
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&i,&j);
       // printf("%d %d %I64d %I64d\n",i,j+1,sum[i],sum[j+1]);
        if(i == j)
            printf("0\n");
        else
            printf("%I64d\n",sum[i]-sum[j]);
    }

    return 0;
}

 

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <string>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <math.h>
#include <bitset>
#include <list>
#include <algorithm>
#include <climits>
using namespace std;

#define lson 2*i
#define rson 2*i+1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 5000005
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define lowbit(x) (x&-x)
const int mod = 1e9+7;
int p[N];
bool v[N]; 
int a[N];
int prime[N/10];
LL sum[N];
void init()
{
    for(int i=2; i<N; ++i)
        a[i] = i;
    int num=-1;
    for(int i=2; i<N; ++i)
    {
        if(!v[i]) prime[++num] = i;
        for(int j=0; j<=num && i*prime[j] < N; ++j)
        {
            int t = i*prime[j];
            v[t] =1;
            if(a[t] > prime[j]) a[t] = prime[j];
            if(i%prime[j] == 0) break;
        }
    }
    p[2] = 1;
    for(int i=3; i <N; ++i)
        p[i] = p[i/a[i]] + 1;
}
int main()
{
    int i,j,k;
    init();
    sum[1] = 0;
    for(i = 2; i<=5000000; i++)
    {
        sum[i] = sum[i-1]+p[i];
    }
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&i,&j);
        if(i == j)
            printf("0\n");
        else
            printf("%I64d\n",sum[i]-sum[j]);
    }

    return 0;
}

 

 

E. Soldier and Traveling

 

In the country there are n cities and m bidirectional roads between them. Each city has an army. Army of the i-th city consists of aisoldiers. Now soldiers roam. After roaming each soldier has to either stay in his city or to go to the one of neighboring cities by at moving along at most one road.

Check if is it possible that after roaming there will be exactly bi soldiers in the i-th city.

Input

First line of input consists of two integers n and m (1 ≤ n ≤ 100, 0 ≤ m ≤ 200).

Next line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 100).

Next line contains n integers b1, b2, ..., bn (0 ≤ bi ≤ 100).

Then m lines follow, each of them consists of two integers p and q (1 ≤ p, q ≤ n, p ≠ q) denoting that there is an undirected road between cities p and q.

It is guaranteed that there is at most one road between each pair of cities.

Output

If the conditions can not be met output single word "NO".

Otherwise output word "YES" and then n lines, each of them consisting of n integers. Number in the i-th line in the j-th column should denote how many soldiers should road from city i to city j (if i ≠ j) or how many soldiers should stay in city i (if i = j).

If there are several possible answers you may output any of them.

Sample test(s)

input

4 4
1 2 6 3
3 5 3 1
1 2
2 3
3 4
4 2

output

YES
1 0 0 0 
2 0 0 0 
0 5 1 0 
0 0 2 1 

input

2 0
1 2
2 1

output

NO

题意：给你一张无向图，每个点有一定数量的人，通过移动可以去邻接点（但是只能移动一次）问你是否能从初始状态移动到目标状态；

思路:网络流+最大流；

转载请注明出处：寻找&星空の孩子

题目链接：http://codeforces.com/contest/546/problem/E

#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
using namespace std;
#define captype int

const int MAXN = 510;   //点的总数
const int MAXM = 400010;    //边的总数
const int INF = 1<<30;
struct EDG{
    int to,next;
    captype cap,flow;
} edg[MAXM];
int eid,head[MAXN];
int gap[MAXN];  //每种距离(或可认为是高度)点的个数
int dis[MAXN];  //每个点到终点eNode 的最短距离
int cur[MAXN];  //cur[u] 表示从u点出发可流经 cur[u] 号边
int pre[MAXN];
int mapt[105][105];

void init(){
    eid=0;
    memset(head,-1,sizeof(head));
    memset(mapt,0,sizeof(mapt));
}
//有向边 三个参数，无向边4个参数
void addEdg(int u,int v,captype c,captype rc=0){
    edg[eid].to=v; edg[eid].next=head[u];
    edg[eid].cap=c; edg[eid].flow=0; head[u]=eid++;

    edg[eid].to=u; edg[eid].next=head[v];
    edg[eid].cap=rc; edg[eid].flow=0; head[v]=eid++;
}
captype maxFlow_sap(int sNode,int eNode, int n){//n是包括源点和汇点的总点个数，这个一定要注意
    memset(gap,0,sizeof(gap));
    memset(dis,0,sizeof(dis));
    memcpy(cur,head,sizeof(head));
    pre[sNode] = -1;
    gap[0]=n;
    captype ans=0;  //最大流
    int u=sNode;
    while(dis[sNode]<n){   //判断从sNode点有没有流向下一个相邻的点
        if(u==eNode){   //找到一条可增流的路
            captype Min=INF ;
            int inser;
            for(int i=pre[u]; i!=-1; i=pre[edg[i^1].to])    //从这条可增流的路找到最多可增的流量Min
            if(Min>edg[i].cap-edg[i].flow){
                Min=edg[i].cap-edg[i].flow;
                inser=i;
            }
            for(int i=pre[u]; i!=-1; i=pre[edg[i^1].to]){

                edg[i].flow+=Min;
                edg[i^1].flow-=Min;  //可回流的边的流量
                
                if(edg[i].to==eNode||edg[i].to==sNode||edg[i^1].to==eNode||edg[i^1].to==sNode)
                    continue;
                if(edg[i].cap>0){
                    int tu, tv;
                    tu=edg[i^1].to; tv=edg[i].to-(n-1)/2;
                    mapt[tu][tv]+=Min;
                }
                else{
                    int tu, tv;
                    tu=edg[i].to; tv=edg[i^1].to-(n-1)/2;
                    mapt[tu][tv]-=Min;
                }
                
            }
            ans+=Min;
            u=edg[inser^1].to;
            continue;
        }
        bool flag = false;  //判断能否从u点出发可往相邻点流
        int v;
        for(int i=cur[u]; i!=-1; i=edg[i].next){
            v=edg[i].to;
            if(edg[i].cap-edg[i].flow>0 && dis[u]==dis[v]+1){
                flag=true;
                cur[u]=pre[v]=i;
                break;
            }
        }
        if(flag){
            u=v;
            continue;
        }
        //如果上面没有找到一个可流的相邻点，则改变出发点u的距离（也可认为是高度）为相邻可流点的最小距离+1
        int Mind= n;
        for(int i=head[u]; i!=-1; i=edg[i].next)
        if(edg[i].cap-edg[i].flow>0 && Mind>dis[edg[i].to]){
            Mind=dis[edg[i].to];
            cur[u]=i;
        }
        gap[dis[u]]--;
        if(gap[dis[u]]==0) return ans;  //当dis[u]这种距离的点没有了，也就不可能从源点出发找到一条增广流路径
                                        //因为汇点到当前点的距离只有一种，那么从源点到汇点必然经过当前点，然而当前点又没能找到可流向的点，那么必然断流
        dis[u]=Mind+1;//如果找到一个可流的相邻点，则距离为相邻点距离+1，如果找不到，则为n+1
        gap[dis[u]]++;
        if(u!=sNode) u=edg[pre[u]^1].to;  //退一条边
    }
    return ans;
}
int main(){
    int n,m ,s , t , u,v,c[105],tc;
    while(scanf("%d%d",&n,&m)>0){
        init();
        s=0;
        t=2*n+1;
        int ans=0;
        for(int i=1; i<=n; i++){
            scanf("%d",&c[i]);
            ans+=c[i];
            addEdg(s,i,c[i]);
            addEdg(i,i+n,c[i]);
        }
        int sum=0;
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&tc); sum+=tc;
            addEdg(i+n,t,tc);
        }
        while(m--){
            scanf("%d%d",&u,&v);
            addEdg(u,v+n,c[u]);
            addEdg(v,u+n,c[v]);
        }
        if(ans!=sum){
            printf("NO\n"); continue;
        }
        ans -= maxFlow_sap(s,t,t+1);
        if(ans==0){
            printf("YES\n");
            for(int i=1; i<=n; i++){
                for(int j=1; j<n; j++)
                    printf("%d ",mapt[i][j]);
                printf("%d\n",mapt[i][n]);
            }
        }
        else
            printf("NO\n");
    }
}