MIT 18.06 linear algebra lecture 20 克拉默法则 逆矩阵 体积 笔记
\(A^{-1}\)的公式
那么如何求\(3\times 3\)或者\(n\times n\)矩阵的逆呢?并且希望利用\(\frac{1}{\text{det }A}\)参与其中,在上面\(2\times 2\)矩阵的例子中,发现有代数余子式矩阵\(\left[\begin{array}{rr}d&-c\\-b&a\end{array}\right]\),在利用行列式求逆矩阵的过程中,代数余子式也参与其中。
事实上:
其中,\(C\)是代数余子式矩阵(注意到转置符号)。\(A\)第一行的代数余子式,对应\(A^{-1}\)中的第一列。
通过代数余子式计算,\(A\)行列式需要将\(n\)项和对应的\(n-1\)矩阵对应的代数余子式相乘,相比这种方法,使用高斯-约尔当消元法求的行列式更为简单。
下面简单验证下\(AC^T=(\text{det }A)I\):
通过乘法得到的矩阵的第一行第一列的元素是:
\(AC^T\)对角线上的每个元素都是上面计算得到的结果。
为了完整证明\(AC^T=(\text{det }A)I\),需要检查\(AC^T\)对角线以外的元素为零。在二乘二的矩阵中,\(A\)的第一行乘\(C^T\)的第二列为 \(a(-b)+b(a)=0\) 。在高维空间中,\(A\)第一行与C^T第二列的乘积可以看作是第一行第二行相同的矩阵(奇异矩阵)的行列式,故乘积为零。所以 \(A^{-1}=\frac{1}{\text{det }A}C^T\) 。通过这个式子,可以了解当矩阵变化时,逆矩阵会如何变化。
克拉默法则(关于 \(\boldsymbol{x}=A^{-1}\boldsymbol{b}\))
如果 \(A\) 是非奇异矩阵时,如果 \(A\boldsymbol{x}=\boldsymbol{b}\) ,则 \(\boldsymbol{x}=A^{-1}\boldsymbol{b}\) ,结合 \(A^{-1}=\frac{C^T}{\text{det }A}\),有:
克拉默(Crammer's rule)法则提供了一种分解上述等式的方式。为了得到克拉默法则,将 \(\boldsymbol{x}\) 的每个部分进行单独分析。因为 \(C^T\boldsymbol{b}\) 的第 \(i\) 部分是一组代数余子式和数字乘积之和,也可以看作是矩阵 \(B_j\)的行列式,则有:
\(B_j\) 是矩阵 \(A\) 中的第 \(j\) 列替换为 \(\boldsymbol{b}\) 得到的:
但是需要记住的是,使用克拉默法则计算并没有使用消元法效率高。
\(|\text{det }A|=\text{盒子的体积}\)
\(|\text{det }A|\) 是由 \(A\) 的列向量组成的平行六面体盒子的体积。(也可以用行向量组成不同的盒子,但是体积是相同的。
如果 \(A=I\) ,则盒子是单位立方体,其体积为 \(1\),与行列式性质一相同
如果 \(A=Q\),且是正交矩阵,则盒子是一个不同方向的单位立方体,体积为 \(1 = |\text{det }Q|\)。(因为 \(Q\)是正交矩阵, \(Q^TQ=I\) ,所以 \(\text{det }Q=\pm1\))。
交换 \(A\)的两列并不改变盒子的体积(记住 \(\text{det }A=\text{det }A^T\))或者行列式的绝对值(行列式性质二)。如果能够证明盒子的体积满足行列式性质三,则可证明 \(|\text{det }A|\) 等于盒子的体积。
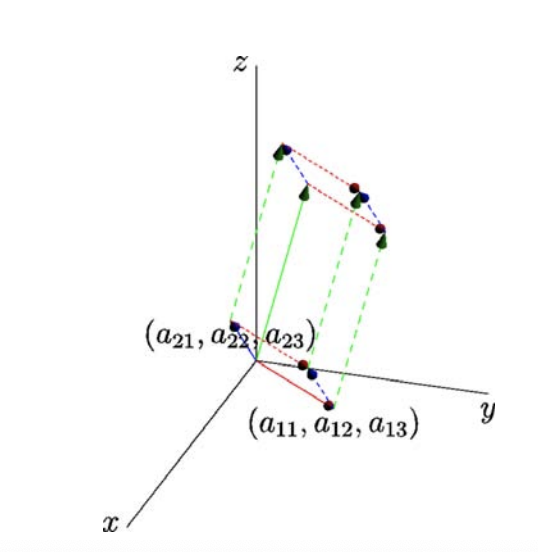
如果将 \(A\) 的某一列乘以 \(2\),则盒子的体积增加 \(2\) 倍,满足性质三(一)。
性质三(二)说明矩阵行列式的和行之间是线性关系:
通过下图,很容易解释同样也是成立的。
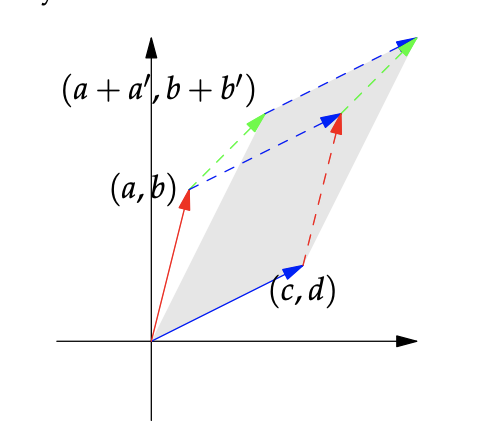
尽管不需证明,还是看看盒子的体积是否满足行列式性质四。如果盒子的两条边是相同的,则盒子会被压扁,没有体积。
注意:如果知道盒子边角的坐标,通过行列式计算盒子的体积非常简单。例如,由 \(\begin{bmatrix}a\\b\end{bmatrix}\) 和 \(\begin{bmatrix}c\\d\end{bmatrix}\)组成的平行四边行面积为 \(ad-bc\) ,则由 \(\begin{bmatrix}a\\b\end{bmatrix}\) 和 \(\begin{bmatrix}c\\d\end{bmatrix}\)组成的三角形的面积为平行四边形的一半, \(\frac{1}{2}(ad-bc)\) 。另外,由 \((x_1,y_1)\), \((x_2,y_2)\) , \((x_3,y_3)\)构成的三角形的面积是:
笔记来源:MIT 18.06 lecture 20



