MIT 18.06 linear algebra lecture 15 子空间投影 笔记

投影

如果有一向量\(\boldsymbol{b}\)和向量\(\boldsymbol{a}\)所在的直线，该直线上哪一点离\(\boldsymbol{b}\)最近？

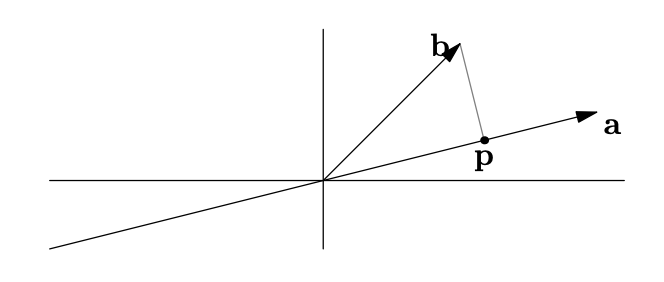
由上图可以看到，经过\(\boldsymbol{b}\)且与\(a\)所正交的直线和\(\boldsymbol{a}\)所在直线的交点\(\boldsymbol{p}\)即是满足上述条件的点。如果将\(\boldsymbol{p}\)看作对\(\boldsymbol{b}\)的近似，则\(\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}\)的长度则是描述近似程度的误差。
通过三角函数或者代数方法能够找到\(\boldsymbol{p}\)，但使用线性代数的方法更为简便。因为\(\boldsymbol{p}\)在\(\boldsymbol{a}\)所在的直线上，所以\(\boldsymbol{p}=x\boldsymbol{a}\)，其中\(x\)是任意实数；另外，\(\boldsymbol{a}\)和\(\boldsymbol{e}=\boldsymbol{b}-x\boldsymbol{a}\)垂直，所以有：

\[\begin{aligned} \boldsymbol{a}^T(\boldsymbol{b}-x\boldsymbol{a})&=0\\ x\boldsymbol{a}^T\boldsymbol{a}&=\boldsymbol{a}^T\boldsymbol{b}\\ x&=\frac{\boldsymbol{a}^T\boldsymbol{b}}{\boldsymbol{a}^T\boldsymbol{a}} \end{aligned} \]

而\(\boldsymbol{p}=\boldsymbol{a}\frac{\boldsymbol{a}^T\boldsymbol{b}}{\boldsymbol{a}^T\boldsymbol{a}}\)
。需要注意的是，当\(\boldsymbol{b}\)放缩时，投影大小也对应放缩；但当\(\boldsymbol{a}\)放缩时，并不影响投影大小。

投影矩阵

将投影操作转化为矩阵：\(\boldsymbol{p}=P\boldsymbol{b}\)：

\[\boldsymbol{b}=x\boldsymbol{a}=\frac{\boldsymbol{a}\boldsymbol{a}^T\boldsymbol{b}}{\boldsymbol{a}^T\boldsymbol{a}} \]

则投影矩阵\(P\)为：

\[P=\frac{\boldsymbol{a}\boldsymbol{a}^T}{\boldsymbol{a}^T\boldsymbol{a}} \]

注意到，\(\boldsymbol{a}\boldsymbol{a}^T\)是一个矩阵，而不是实数，并且矩阵乘法不满足交换律。
\(P\)的列空间由\(\boldsymbol{a}\)生成，因为对于任意\(\boldsymbol{b}\)，\(P\boldsymbol{b}\)均在由\(\boldsymbol{a}\)确定的直线上，矩阵\(P\)的秩为\(1\)；\(P\)是对称的；\(P^2\boldsymbol{b}=P\boldsymbol{b}\)，因为对投影后的向量再进行投影，最终还是在\(a\)所在直线的同一点上。所以通常投影矩阵具有下述性质：

\[P^T=P \]

\[P^2=P \]

投影有什么用？

在上一节提到，\(A\boldsymbol{x}=\boldsymbol{b}\)可能没有解，向量\(A\boldsymbol{x}\)在\(A\)的列空间中，但是\(\boldsymbol{b}\)不一定在列空间中，所以将\(\boldsymbol{b}\)投影到\(A\)的列空间中的\(\boldsymbol{p}\)，然后解\(A\hat{\boldsymbol{x}}=\boldsymbol{p}\)

高维空间中的投影

在\(\mathbb{R}^3\)中，如何将向量\(\boldsymbol{b}\)投影到在平面中离\(\boldsymbol{b}\)最近的向量\(\boldsymbol{p}\)上呢？
假设\(\boldsymbol{a_1}\)和\(\boldsymbol{a_2}\)构成平面的基，该平面也是矩阵\(A=\begin{bmatrix}\boldsymbol{a_1}&\boldsymbol{a_2}\end{bmatrix}\)的列空间。
因为\(\boldsymbol{p}\)是平面内的向量，所以\(\boldsymbol{p}=\hat{x}_1\boldsymbol{a}_1+\hat{x_2}\boldsymbol{a}_2=A\hat{\boldsymbol{x}}\)，接下来是找到\(\boldsymbol{\hat{x}}\)。\(\boldsymbol{p}\)和\(\boldsymbol{b}\)的误差\(\boldsymbol{e}=\boldsymbol{b}-\boldsymbol{p}=\boldsymbol{b}-A\hat{\boldsymbol{x}}\)与投影的平面正交，所以\(\boldsymbol{e}\)和\(\boldsymbol{a}_1\)、\(\boldsymbol{a}_2\)垂直：

\[\boldsymbol{a}^T_1(\boldsymbol{b}-A\boldsymbol{\hat{x}})=0\quad\text{and}\quad\boldsymbol{a}^T_2(\boldsymbol{b}-A\boldsymbol{\hat{x}})=0 \]

上式转换为矩阵形式有，\(A^T(\boldsymbol{b}-A\boldsymbol{\hat{x}})=\boldsymbol{0}\)，当投影到一条线上时，\(A\)仅有一列，所以等式为：\(a^T(\boldsymbol{b}-\boldsymbol{\hat{x}}a)=0\)
注意到，\(\boldsymbol{e}=\boldsymbol{b}-A\boldsymbol{\hat{x}}\)在\(A^T\)的零空间中，在\(A\)的左零空间中。此前已经了解到，\(A\)的左零空间与\(A\)的列空间是正交的，所以侧面证明上面的计算是正确的。
重写等式\(A^T(\boldsymbol{b}-A\boldsymbol{\hat{x}})=\boldsymbol{0}\)，得到：

\[A^TA\hat{\boldsymbol{x}}=A^T\boldsymbol{b} \]

当投影到一条直线时，\(A^TA\)是个实数；现在则是一个方阵，所以用乘逆矩阵\((A^TA)^{-1}\)的方式代替除以\(\boldsymbol{a}^T\boldsymbol{a}\)。
在\(n\)维情况下：

\[\begin{aligned} \hat{\boldsymbol{x}}&=(A^TA)^{-1}A^T\boldsymbol{b}\\ \boldsymbol{p}=A\hat{\boldsymbol{x}}&=A(A^TA)^{-1}A^T\boldsymbol{b}\\ P&=A(A^TA)^{-1}A^T \end{aligned} \]

上面的运算结果貌似可以化简，但是当\(A\)不是方阵的时候，\((A^TA)^{-1}=A^{-1}(A^T)^{-1}\)并不成立，该等式仅在\(A\)是一个方阵且可逆的情况，列空间包括整个空间并且\(\boldsymbol{b}\)也在其中。容易证明，在高维空间中，仍然有：

\[P^T=P \]

\[P^2=P \]

最小二乘

假设当前有一组数据点的集合\((t,b)\)：

\[\lbrace (1,1),(2,2),(3,2)\rbrace \]

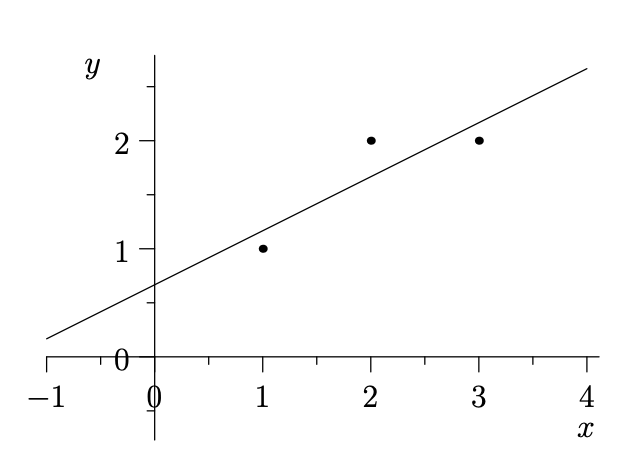
接下来找到想找一条最近的直线\(b=C+Dt\)去拟合数据集，如果有直线经过所有的点，有：

\[\begin{aligned} C+D&=1\\ C+2D&=2\\ C+3D&=2 \end{aligned} \]

上述等式等同于：

\[\begin{array}{ccc} \begin{bmatrix} 1 & 1\\ 1 & 2\\ 1 & 3\\ \end{bmatrix}& \begin{bmatrix} C\\ D \end{bmatrix}& =& \begin{bmatrix} 1\\ 2\\ 2 \end{bmatrix}\\ A&\boldsymbol{x}&&\boldsymbol{b} \end{array} \]

但是在例子中，并找不到一条直线能通过三个点，方程组是无解的，在下一节将通过解\(A^TA\hat{\boldsymbol{x}}=A^T\boldsymbol{b}\)得到一个最佳近似解。

---

笔记来源：MIT 18.06 lecture 15