MIT 18.06 linear algebra lecture 12 图和网络 笔记

借助矩阵和向量这些线性代数中的工具，能够使我们更好地理解其它科学中的系统。例如化学家通常使用行向量化简更好地理解哪些元素参与了复杂的化学反应。本节课中将探讨线性代数在电路中的应用。

图和网络

图（graph）是一些由边连接的节点的集合。下图展示了一幅小图的节点数\(n=4\)，边数\(m=5\)：

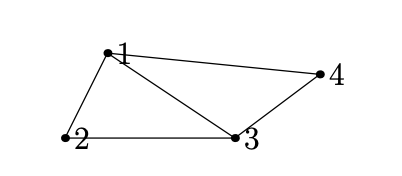
在图中的边上添上箭头，代表通过当前边的电流方向。

关联矩阵

下面关联矩阵（incidence matrix）的每列代表图中的一个节点，每行代表图中的一条边：

\[A= \left[\begin{array}{rrrr} -1 & 1 & 0 & 0\\ 0 & -1 & 1 & 0\\ -1 & 0 & 1 & 0\\ -1 & 0 & 0 & 1\\ 0 & 0 & -1 & 1 \end{array}\right] \]

如果一条边由节点\(a\)到节点\(b\)，对应这条边的行中，第\(a\)列为\(-1\)，第\(b\)列为\(1\)，其余的元素为\(0\)。对于更大的图，将会得到一个大的稀疏矩阵，其中大部分元素为\(0\)。
注意到，节点\(1\)、节点\(2\)和节点\(3\)通过边\(1\)、\(2\)和\(3\)构成一个回路。描述这些节点和边的矩阵如下：

\[\left[\begin{array}{rrrr} -1 & 1 & 0 & 0\\ 0 & -1 & 1 & 0\\ -1 & 0 & 1 & 0 \end{array}\right] \]

显然，上面矩阵中，第三行是第一行和第二行之和：图中的回路对应矩阵中线性相关的行。
为了寻找\(A\)的零空间，解\(A\boldsymbol{x}=\boldsymbol{0}\)：

\[A\boldsymbol{x}= \begin{bmatrix} x_2-x_1\\ x_3-x_2\\ x_3-x_1\\ x_4-x_1\\ x_4-x_3 \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0 \end{bmatrix} \]

如果向量\(\boldsymbol{x}\)中的\(x_i\)描述节点\(i\)的电势，则\(A\boldsymbol{x}\)是描述每条边的节点间电势差的向量。当\(x_1=x_2=x_3=x_4\)时，\(A\boldsymbol{x}=\boldsymbol{0}\)，所以零空间的维数为\(1\)。在电路中，当两个节点间电势相同时，两点见的电势差为零。

矩阵\(A\)的有\(4\)列，并且零空间维数为\(1\)，所以秩为\(3\)。第\(1\)、\(2\)、\(4\)列为主元列；图中连接所有节点的边并不构成一个回路，称为树。

\(A\)的左零空间由\(A^T\boldsymbol{y}=\boldsymbol{0}\)的解\(\boldsymbol{y}\)组成。因为\(A^T\)有\(5\)列并且秩为\(3\)，所以\(N(A^T)\)的维数为\(m-r=2\)。注意到，\(2\)是图中环(loop)的个数，而\(m\)是节点的个数，秩\(r\)为\(n-1\)，小于节点的个数。给了个结论：#loops = #edges - (#nodes - 1)，或者：

\[\text{number of nodes } -\text{number of edges }+\text{number of loops }=1 \]

上述即是连接图中的欧拉公式。

---

笔记来源：MIT 18.06 lecture 12

本节后半部分关于矩阵及基尔霍夫电流定律的关系没有记录，感兴趣的可以通过上面的笔记连接进一步了解。