7-3 树的同构（25 分）

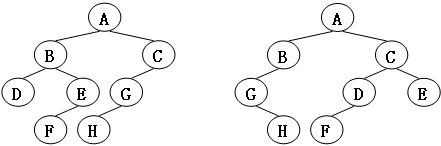
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 


 

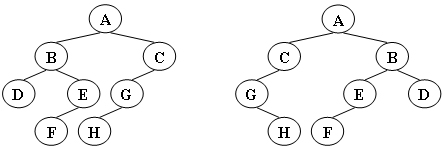
图1

图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
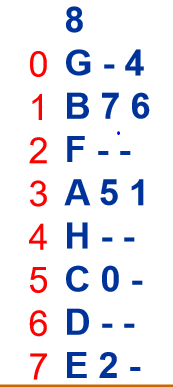
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:No


题意理解： 题目输入的意思是字母后面的数字代表它的子树在那个位置上，
           如G的右子树标记为4代表G的右子树是位置4上的H
           
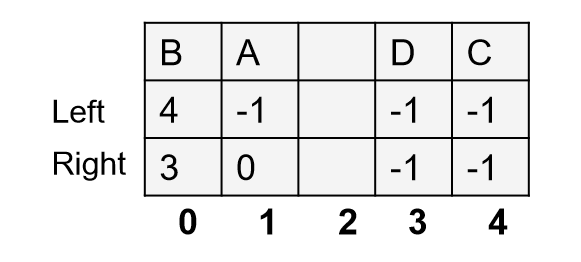
解决思路：1.关键是采用静态链表
           
          2.还有一个难点是如何确定根节点，这里创建一个check数组，若在静态链表中
            未出现的下标则为根节点，如上图A结点的下标1在静态链表中未出现，因而
            判断A是根节点
  1 #include <stdio.h>
  2 #include <stdlib.h>
  3 
  4 #define MaxTree 10
  5 #define ElementType char
  6 #define Tree int
  7 #define Null -1
  8 
  9 struct TreeNode
 10 {
 11     ElementType e;
 12     Tree left;
 13     Tree right;
 14 }T1[MaxTree],T2[MaxTree];
 15 
 16 Tree BuildTree ( struct TreeNode T[]);
 17 int Isomorphic(Tree R1,Tree R2);
 18 
 19 int main()
 20 {
 21     Tree R1,R2;
 22 
 23     R1 = BuildTree(T1);
 24     R2 = BuildTree(T2);
 25     if( Isomorphic(R1,R2)){
 26         printf("Yes\n");
 27     }
 28     else{
 29         printf("No\n");
 30     }
 31     return 0;
 32 
 33 }
 34 
 35 Tree BuildTree ( struct TreeNode T[])
 36 {
 37 
 38     int i;
 39     int n;
 40     int check[MaxTree];
 41     char cl,cr;
 42     Tree root =Null;   //若n为0，返回Null
 43     
 44     scanf("%d",&n);
 45     if( n ){
 46         for( i=0; i<n; i++){
 47             check[i] = 0;
 48         }
 49         for( i=0; i<n; i++){
 50             scanf("\n%c %c %c",&T[i].e,&cl,&cr);
 51             if( cl!='-' ){
 52                 T[i].left = cl-'0';   //若输入不为'-',那字符减去字符0转换为整型数值
 53                 check[T[i].left] = 1; //把在静态链表中出现过的数值标记为1
 54             }
 55             else if( cl=='-' ){
 56                 T[i].left = Null;
 57             }
 58             if( cr!='-' ){
 59                 T[i].right = cr-'0';
 60                 check[T[i].right] = 1;
 61             }
 62             else if( cr=='-' ){
 63                 T[i].right = Null;
 64             }
 65         }
 66 
 67         for( i=0; i<n; i++){
 68             if( !check[i]){
 69                 break;
 70             }
 71         }
 72         root = i;
 73 
 74     }
 75     return root;
 76 }
 77 
 78 int Isomorphic(Tree R1,Tree R2){
 79     if((R1==Null)&&(R2==Null))      //如果为空树则是同构的
 80         return 1;
 81         
 82     if(((R1==Null)&&(R2!=Null))||((R1!=Null)&&(R2==Null)))//如果一个为空一个不为空则不是同构的
 83         return 0;
 84         
 85     if((T1[R1].e)!=(T2[R2].e))//如果数据不同则不是同构的
 86         return 0;
 87         
 88     //如果左儿子都为空判断右儿子是否同构
 89     if((T1[R1].left==Null)&&(T2[R2].left==Null))
 90         return Isomorphic(T1[R1].right,T2[R2].right);
 91         
 92     /* 如果两棵树左儿子都不为空并且数据还是一样的，对左儿子进行递归*/
 93     if ( ((T1[R1].left!=Null)&&(T2[R2].left!=Null))&&((T1[T1[R1].left].e)==(T2[T2[R2].left].e)) )
 94         return ( Isomorphic( T1[R1].left, T2[R2].left )&&Isomorphic( T1[R1].right, T2[R2].right ) );
 95         
 96     /* 如果两棵树左儿子（一个空一个不空或者都不空）并且数据不一样，
 97     那么判断第一棵树的左（右）儿子是否跟第二棵树的右（左）儿子同构 */
 98     else
 99         return ( Isomorphic( T1[R1].left, T2[R2].right)&&Isomorphic( T1[R1].right, T2[R2].left ) );
100 
101 }

 

这道题个人觉得还是比较难，如果觉得难以理解可以看中国大学慕课浙江大学数据结构课程讲解

 

 




posted @ 2018-01-22 17:04  yuxiaoba  阅读(3917)  评论(0)  编辑  收藏  举报