Sklearn之支持向量机分类
''' 支持向量机: 支持向量机原理: 分类原则:寻求最优分类边界 1.正确:对大部分样本可以正确地划分类别。 2.泛化:最大化支持向量间距。 3.公平:与支持向量等距。 4.简单:线性,直线或平面,分割超平面。 基于核函数的升维变换:通过名为核函数的特征变换,增加新的特征,使得低维度空间中的线性不可分问题变为高维度空间中的线性可分问题。 1>线性核函数:linear,不通过核函数进行维度提升,仅在原始维度空间中寻求线性分类边界。 2>多项式核函数:poly,通过多项式函数增加原始样本特征的高次方幂 y = x_1+x_2 y = x_1^2 + 2x_1x_2 + x_2^2 y = x_1^3 + 3x_1^2x_2 + 3x_1x_2^2 + x_2^3 3>径向基核函数:rbf,通过高斯分布函数增加原始样本特征的分布概率 基于线性核函数的SVM分类相关API: model = svm.SVC(kernel='linear') model.fit(train_x, train_y) 案例,基于径向基核函数训练sample2.txt中的样本数据。 步骤: 1.读取文件,绘制样本点的分布情况 2.拆分测试集合训练集 3.基于svm训练分类模型 4.输出分类效果,绘制分类边界 ''' import numpy as np import sklearn.model_selection as ms import sklearn.svm as svm import sklearn.metrics as sm import matplotlib.pyplot as mp data = np.loadtxt('./ml_data/multiple2.txt', delimiter=',', unpack=False, dtype='f8') x = data[:, :-1] y = data[:, -1] # 才分训练集和测试集 train_x, test_x, train_y, test_y = ms.train_test_split(x, y, test_size=0.25, random_state=5) # 训练svm模型---基于线性核函数 # model = svm.SVC(kernel='linear') # model.fit(train_x, train_y) # 训练svm模型---基于多项式核函数 # model = svm.SVC(kernel='poly', degree=3) # model.fit(train_x, train_y) # 训练svm模型---基于径向基核函数 model = svm.SVC(kernel='rbf', C=600) model.fit(train_x, train_y) # 预测 pred_test_y = model.predict(test_x) # 计算模型精度 bg = sm.classification_report(test_y, pred_test_y) print('分类报告:', bg, sep='\n') # 绘制分类边界线 l, r = x[:, 0].min() - 1, x[:, 0].max() + 1 b, t = x[:, 1].min() - 1, x[:, 1].max() + 1 n = 500 grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n)) bg_x = np.column_stack((grid_x.ravel(), grid_y.ravel())) bg_y = model.predict(bg_x) grid_z = bg_y.reshape(grid_x.shape) # 画图显示样本数据 mp.figure('SVM Classification', facecolor='lightgray') mp.title('SVM Classification', fontsize=16) mp.xlabel('X', fontsize=14) mp.ylabel('Y', fontsize=14) mp.tick_params(labelsize=10) mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray') mp.scatter(test_x[:, 0], test_x[:, 1], s=80, c=test_y, cmap='jet', label='Samples') mp.legend() mp.show() 输出结果: 分类报告: precision recall f1-score support 0.0 0.91 0.87 0.89 45 1.0 0.81 0.87 0.84 30 accuracy 0.87 75 macro avg 0.86 0.87 0.86 75 weighted avg 0.87 0.87 0.87 75
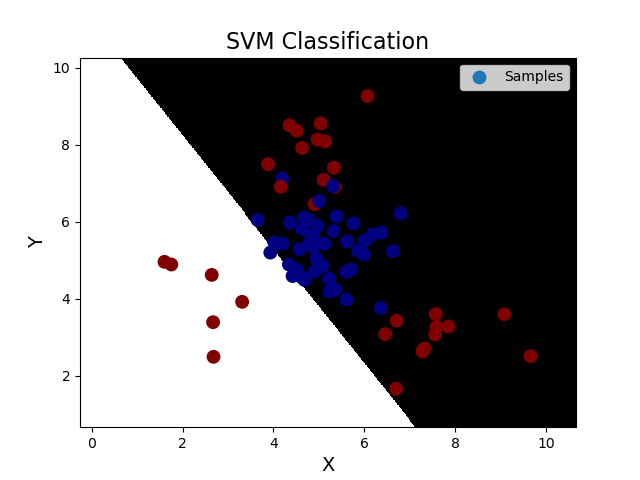
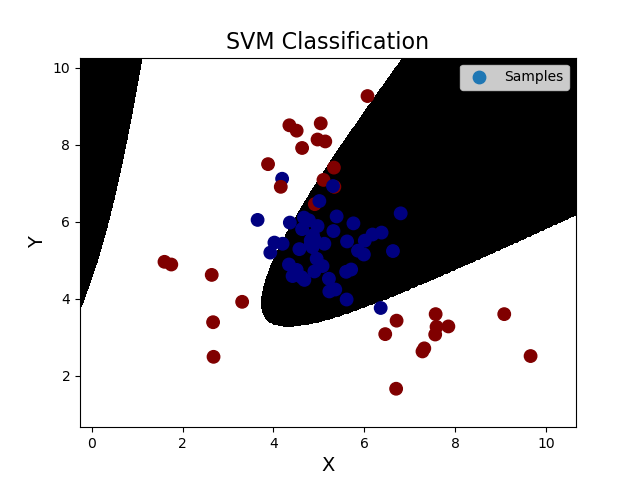
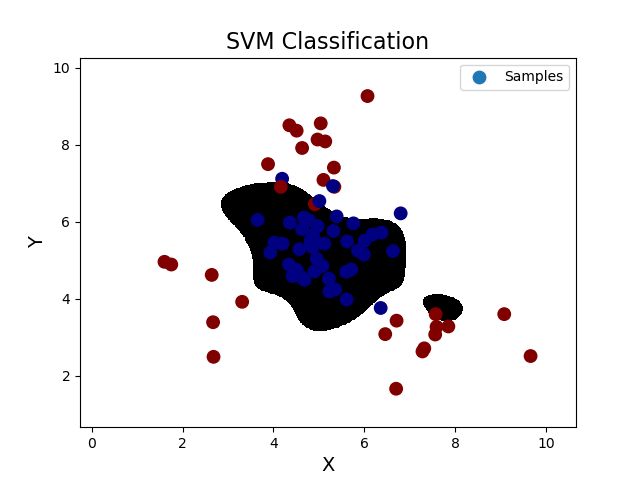
''' 支持向量机分类之样本类别均衡化:通过类别权重的均衡化,使所占比例较小的样本权重较高,而所占比例较大的样本权重较低, 以此平均化不同类别样本对分类模型的贡献,提高模型性能。 样本类别均衡化相关API: model = svm.SVC(kernel='linear', class_weight='balanced') model.fit(train_x, train_y) 案例:修改线性核函数的支持向量机案例,基于样本类别均衡化读取imbalance.txt训练模型。 ''' import numpy as np import sklearn.model_selection as ms import sklearn.svm as svm import sklearn.metrics as sm import matplotlib.pyplot as mp data = np.loadtxt('./ml_data/imbalance.txt', delimiter=',', unpack=False, dtype='f8') x = data[:, :-1] y = data[:, -1] # 才分训练集和测试集 train_x, test_x, train_y, test_y = ms.train_test_split(x, y, test_size=0.25, random_state=5) # 训练svm模型---基于线性核函数 model = svm.SVC(kernel='linear', class_weight='balanced') model.fit(train_x, train_y) # 预测 pred_test_y = model.predict(test_x) # 计算模型精度 bg = sm.classification_report(test_y, pred_test_y) print('分类报告:', bg, sep='\n') # 绘制分类边界线 l, r = x[:, 0].min() - 1, x[:, 0].max() + 1 b, t = x[:, 1].min() - 1, x[:, 1].max() + 1 n = 500 grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n)) bg_x = np.column_stack((grid_x.ravel(), grid_y.ravel())) bg_y = model.predict(bg_x) grid_z = bg_y.reshape(grid_x.shape) # 画图显示样本数据 mp.figure('SVM Classification', facecolor='lightgray') mp.title('SVM Classification', fontsize=16) mp.xlabel('X', fontsize=14) mp.ylabel('Y', fontsize=14) mp.tick_params(labelsize=10) mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray') mp.scatter(test_x[:, 0], test_x[:, 1], s=80, c=test_y, cmap='jet', label='Samples') mp.legend() mp.show() 输出结果: 分类报告: precision recall f1-score support 0.0 0.35 0.14 0.20 42 1.0 0.87 0.96 0.91 258 accuracy 0.84 300 macro avg 0.61 0.55 0.56 300 weighted avg 0.80 0.84 0.81 300
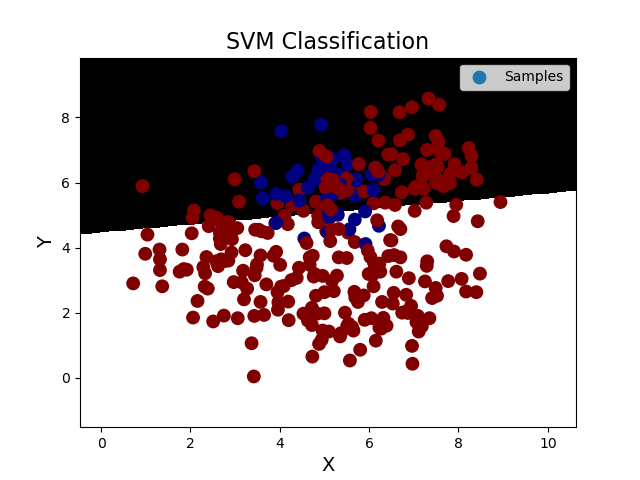
上图可见,该样本数据的样本类别区分度不好,选区的特征无法区分类别,遇到这种情况,通常要考虑增加样本特征,以提高类别区分度
''' 支持向量机之置信概率:根据样本与分类边界的距离远近,对其预测类别的可信程度进行量化,离边界越近的样本,置信概率越低, 反之,离边界越远的样本,置信概率高。 获取每个样本的置信概率相关API: # 在获取模型时,给出超参数probability=True model = svm.SVC(kernel='rbf', C=600, gamma=0.01, probability=True) 预测结果 = model.predict(输入样本矩阵) # 调用model.predict_proba(样本矩阵)可以获取每个样本的置信概率矩阵 置信概率矩阵 = model.predict_proba(输入样本矩阵) 置信概率矩阵格式如下: 类别1 类别2 样本1 0.8 0.2 样本2 0.9 0.1 样本3 0.5 0.5 案例:修改基于径向基核函数的SVM案例,新增测试样本,输出每个测试样本的置信概率,并给出标注。 ''' import numpy as np import sklearn.model_selection as ms import sklearn.svm as svm import sklearn.metrics as sm import matplotlib.pyplot as mp data = np.loadtxt('./ml_data/multiple2.txt', delimiter=',', unpack=False, dtype='f8') x = data[:, :-1] y = data[:, -1] # 才分训练集和测试集 train_x, test_x, train_y, test_y = ms.train_test_split(x, y, test_size=0.25, random_state=5) # 训练svm模型---基于径向基核函数 model = svm.SVC(kernel='rbf', C=600, gamma=0.01, probability=True) model.fit(train_x, train_y) # 自定义一组测试样本,输出样本的置信概率 prob_x = np.array([ [2, 1.5], [8, 9], [4.8, 5.2], [4, 4], [2.5, 7], [7.6, 2], [5.4, 5.9]]) pred_prob_y = model.predict(prob_x) probs = model.predict_proba(prob_x) print('自信概率为:', probs, sep='\n') # 计算模型精度 # bg = sm.classification_report(test_y, pred_test_y) # print('分类报告:', bg, sep='\n') # 绘制分类边界线 l, r = x[:, 0].min() - 1, x[:, 0].max() + 1 b, t = x[:, 1].min() - 1, x[:, 1].max() + 1 n = 500 grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n)) bg_x = np.column_stack((grid_x.ravel(), grid_y.ravel())) bg_y = model.predict(bg_x) grid_z = bg_y.reshape(grid_x.shape) # 画图显示样本数据 mp.figure('SVM Classification', facecolor='lightgray') mp.title('SVM Classification', fontsize=16) mp.xlabel('X', fontsize=14) mp.ylabel('Y', fontsize=14) mp.tick_params(labelsize=10) mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray') mp.scatter(test_x[:, 0], test_x[:, 1], s=80, c=test_y, cmap='jet', label='Samples') mp.scatter(prob_x[:, 0], prob_x[:, 1], c='orange', s=100, label='prob_samples') # 为每一个点添加备注,标注置信概率 for i in range(len(probs)): mp.annotate( '[{:.2f}%,{:.2f}%]'.format(probs[i][0]*100, probs[i][1]*100), xy=prob_x[i], xytext=(-10, 30), xycoords='data', textcoords='offset points', arrowprops=dict(arrowstyle='-|>', connectionstyle='angle3'), fontsize=10, color='red' ) mp.legend() mp.show() 输出结果为: 自信概率为: [[3.00000090e-14 1.00000000e+00] [3.00000090e-14 1.00000000e+00] [9.76198900e-01 2.38011003e-02] [5.86133509e-01 4.13866491e-01] [2.80092352e-03 9.97199076e-01] [2.50983575e-11 1.00000000e+00] [9.49824497e-01 5.01755028e-02]]




