sklearn之分类模型混淆矩阵和分类报告
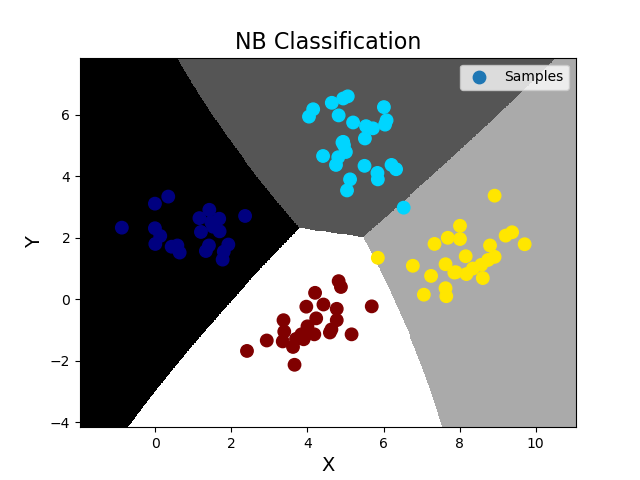
''' 1.分类模型之混淆矩阵: 每一行和每一列分别对应样本输出中的每一个类别,行表示实际类别,列表示预测类别。 A类别 B类别 C类别 A类别 5 0 0 B类别 0 6 0 C类别 0 0 7 上述矩阵即为理想的混淆矩阵。不理想的混淆矩阵如下: A类别 B类别 C类别 A类别 3 1 1 B类别 0 4 2 C类别 0 0 7 查准率 = 主对角线上的值 / 该值所在列的和 召回率 = 主对角线上的值 / 该值所在行的和 获取模型分类结果的混淆矩阵的相关API: import sklearn.metrics as sm sm.confusion_matrix(实际输出, 预测输出)->混淆矩阵 2.分类模型之分类报告: sklearn.metrics提供了分类报告相关API,不仅可以得到混淆矩阵,还可以得到交叉验证查准率、召回率、f1得分的结果, 可以方便的分析出哪些样本是异常样本。 # 获取分类报告 cr = sm.classification_report(实际输出, 预测输出) ''' import numpy as np import matplotlib.pyplot as mp import sklearn.naive_bayes as nb import sklearn.model_selection as ms import sklearn.metrics as sm data = np.loadtxt('./ml_data/multiple1.txt', delimiter=',', unpack=False, dtype='f8') print(data.shape) x = np.array(data[:, :-1]) y = np.array(data[:, -1]) # 训练集和测试集的划分 使用训练集训练 再使用测试集测试,并绘制测试集样本图像 train_x, test_x, train_y, test_y = ms.train_test_split(x, y, test_size=0.25, random_state=7) # 针对训练集,做5次交叉验证,若得分还不错再训练模型 model = nb.GaussianNB() # 精确度 score = ms.cross_val_score(model, train_x, train_y, cv=5, scoring='accuracy') print('accuracy score=', score) print('accuracy mean=', score.mean()) # 查准率 score = ms.cross_val_score(model, train_x, train_y, cv=5, scoring='precision_weighted') print('precision_weighted score=', score) print('precision_weighted mean=', score.mean()) # 召回率 score = ms.cross_val_score(model, train_x, train_y, cv=5, scoring='recall_weighted') print('recall_weighted score=', score) print('recall_weighted mean=', score.mean()) # f1得分 score = ms.cross_val_score(model, train_x, train_y, cv=5, scoring='f1_weighted') print('f1_weighted score=', score) print('f1_weighted mean=', score.mean()) # 训练NB模型,完成分类业务 model.fit(train_x, train_y) pred_test_y = model.predict(test_x) # 得到预测输出,可以与真实输出作比较,计算预测的精准度(预测正确的样本数/总测试样本数) ac = (test_y == pred_test_y).sum() / test_y.size print('预测精准度 ac=', ac) # 获取混淆矩阵 m = sm.confusion_matrix(test_y, pred_test_y) print('混淆矩阵为:', m, sep='\n') # 获取分类报告 r = sm.classification_report(test_y, pred_test_y) print('分类报告为:', r, sep='\n') # 绘制分类边界线 l, r = x[:, 0].min() - 1, x[:, 0].max() + 1 b, t = x[:, 1].min() - 1, x[:, 1].max() + 1 n = 500 grid_x, grid_y = np.meshgrid(np.linspace(l, r, n), np.linspace(b, t, n)) bg_x = np.column_stack((grid_x.ravel(), grid_y.ravel())) bg_y = model.predict(bg_x) grid_z = bg_y.reshape(grid_x.shape) # 画图 mp.figure('NB Classification', facecolor='lightgray') mp.title('NB Classification', fontsize=16) mp.xlabel('X', fontsize=14) mp.ylabel('Y', fontsize=14) mp.tick_params(labelsize=10) mp.pcolormesh(grid_x, grid_y, grid_z, cmap='gray') mp.scatter(test_x[:, 0], test_x[:, 1], s=80, c=test_y, cmap='jet', label='Samples') mp.legend() mp.show() # 画出混淆矩阵 mp.figure('Confusion Matrix') mp.xticks([]) mp.yticks([]) mp.imshow(m, cmap='gray') mp.show() 输出结果: (400, 3) accuracy score= [1. 1. 1. 1. 0.98305085] accuracy mean= 0.9966101694915255 precision_weighted score= [1. 1. 1. 1. 0.98411017] precision_weighted mean= 0.996822033898305 recall_weighted score= [1. 1. 1. 1. 0.98305085] recall_weighted mean= 0.9966101694915255 f1_weighted score= [1. 1. 1. 1. 0.98303199] f1_weighted mean= 0.9966063988235516 预测精准度 ac= 0.99 混淆矩阵为: [[22 0 0 0] [ 0 27 1 0] [ 0 0 25 0] [ 0 0 0 25]] 分类报告为: precision recall f1-score support 0.0 1.00 1.00 1.00 22 1.0 1.00 0.96 0.98 28 2.0 0.96 1.00 0.98 25 3.0 1.00 1.00 1.00 25 accuracy 0.99 100 macro avg 0.99 0.99 0.99 100 weighted avg 0.99 0.99 0.99 100