numpy之傅里叶定理
一、基于傅里叶定理,用一组正弦函数合成方波
''' 三角函数通用函数 傅里叶定理:任何一个周期性曲线,无论多么跳跃或者不规则,都可以被解析成一组光滑的正弦函数的叠加 ---应用:合成方波(即不规则的方波由一组光滑的正弦函数叠加合成的) 如:y = 4π/(2*n-1) * sin((2*n-1)*x) ''' import numpy as np import matplotlib.pyplot as mp x = np.linspace(-2 * np.pi, 2 * np.pi, 1000) y1 = 4 * np.pi * np.sin(x) y2 = 4 * np.pi / 3 * np.sin(3 * x) n = 6 y = np.zeros(1000) for i in range(1, n + 1): y += 4 * np.pi / (2 * i - 1) * np.sin((2 * i - 1) * x) mp.plot(x, y1, label='y1', alpha=0.3) mp.plot(x, y2, label='y2', alpha=0.3) mp.plot(x, y, label='y') mp.legend() mp.show()

二、基于快速傅里叶变换实现方波的拆解
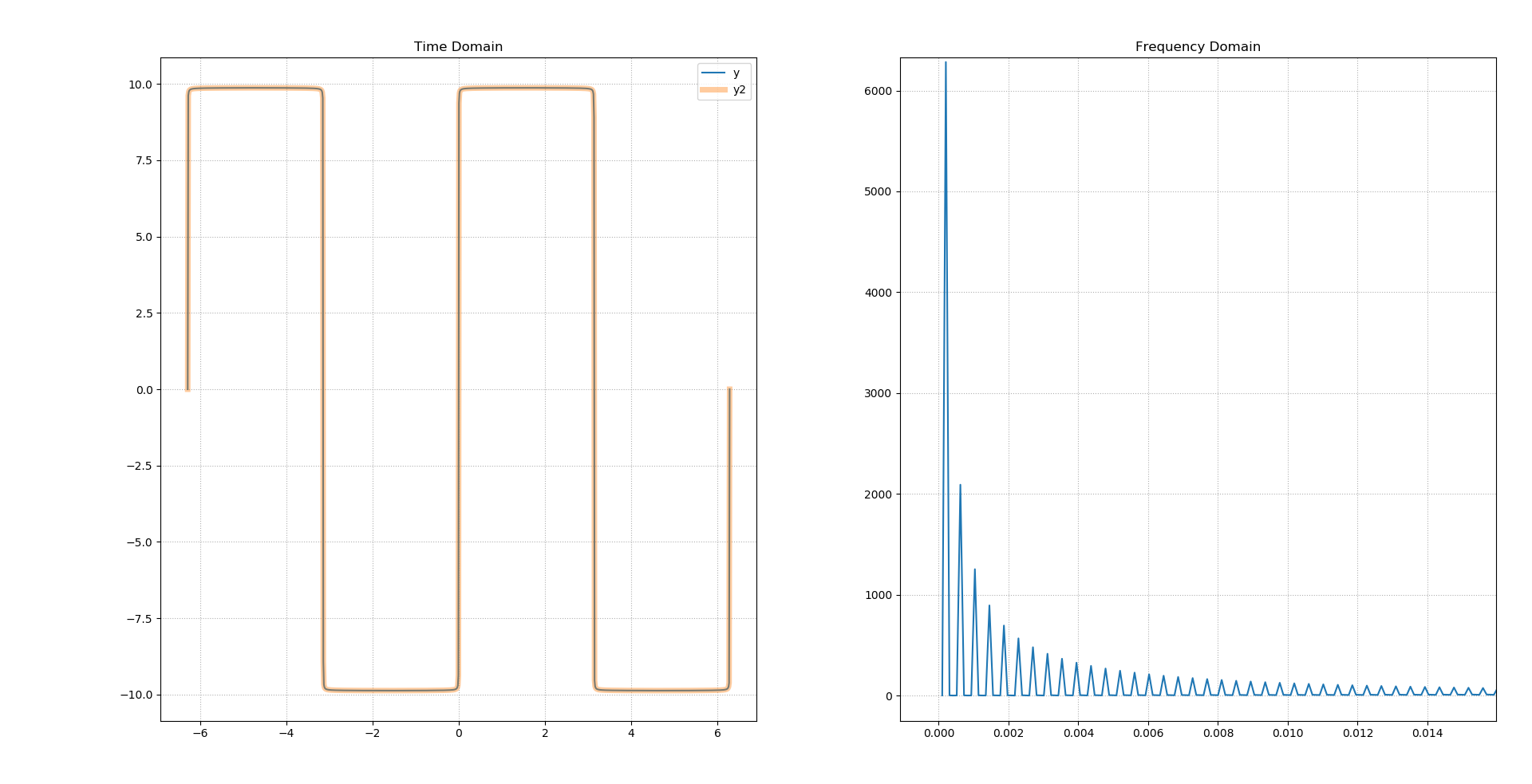
''' 傅里叶变换:即是将一条周期性忑基于傅里叶定理进行拆解,得到一组光滑的正弦曲线的变换过程 傅里叶变化的目的:是可将时间域的信号转换为频域(频率域)信号,随着域的不同,对同一个事物的了解角度也就随之改变, 因此在时域中某些不好处理的地方,在频域中可以较为简单的处理,如:数据存储、数据降噪等 傅里叶变换主要运用在音频文件领域 在numpy中有一个专门模块---fft模块,专门处理傅里叶变换 ---复数数组 = fft.fft(原函数y的数组) --->即为快速傅里叶变换 --复数数组中的每个复数可以描述一条正弦曲线,复数的模代表振幅A,复数的辅角代表初相位角φ ---freqs = fft.fftfreq(采样数量,采样周期) -->通过采样数和采样周期求得曲线的频率序列,即ω ---逆向傅里叶变换 -- y2 = fft.ifft(复数数组) 案例:拆解方波,绘制图像 ''' import numpy as np import matplotlib.pyplot as mp import numpy.fft as fft x = np.linspace(-2 * np.pi, 2 * np.pi, 1000) # 合成方波 n = 1000 y = np.zeros(1000) for i in range(1, n + 1): y += 4 * np.pi / (2 * i - 1) * np.sin((2 * i - 1) * x) # 拆解方波 freqs = fft.fftfreq(y.size, y[1] - y[0]) complex_ary = fft.fft(y) print(complex_ary.size) # 逆向傅里叶变换 y2 = fft.ifft(complex_ary) # 绘制时域图 mp.figure('FFT') mp.subplot(121) mp.title('Time Domain') mp.plot(x, y, label='y') mp.plot(x, y2, linewidth=5, label='y2', alpha=0.4) mp.grid(linestyle=":") mp.legend() # 绘制频域图 mp.subplot(122) mp.title('Frequency Domain') mp.grid(linestyle=":") power = np.abs(complex_ary) mp.plot(freqs[freqs > 0], power[freqs > 0]) mp.tight_layout() mp.show()
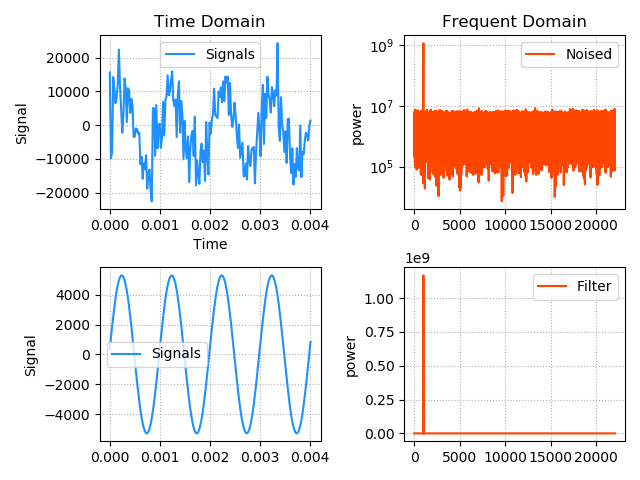
三、基于傅里叶变换的频域滤波
''' 基于傅里叶变换的频域滤波 ----过滤音频中噪声:含噪信号由高能信号与低能噪声叠加而成,可以通过FFT的频域滤波实现降噪。通过FFT使含噪信号转为含噪频谱, 留下高能频谱,过滤掉低能噪声,再经过IFFT将高能频谱生成高能信号。 步骤: 1.读取音频文件,获取音频文件的基本信息:采样率、采样周期、每个采样点的声音位移值。绘制音频的时域(时间/位移)图像 2.基于傅里叶变换,获取音频频域信息,绘制音频的频域(频率/能量)图像 3.将低能噪声去除,绘制音频频域(频域/能量)图像 4.基于逆向傅里叶变换(ifft),生成新的音频信号,绘制图像 5.生成音频文件 ''' import scipy.misc as sc import matplotlib.pyplot as mp import numpy as np import scipy.io.wavfile as wf # 读取音频文件模块 import numpy.fft as nf # 傅里叶变换模块 import warnings warnings.filterwarnings("ignore") # 第一步骤 # 读取音频文件,获取采样率(每秒采样多少个点)和采样点位移(一共采样多少个点) sample_rate, noise_sigs = wf.read('./da_data/noised.wav') # print('sample_rate:', sample_rate) # print('noise_sigs:', noise_sigs.shape) # 计算采样时间 times = np.arange(len(noise_sigs)) / sample_rate print(times.shape) mp.figure('Filter', facecolor='lightgray') mp.subplot(221) mp.title('Time Domain') mp.xlabel('Time') mp.ylabel('Signal') mp.grid(linestyle=':') # 因数据太大,只取前178个 mp.plot(times[:178], noise_sigs[:178], c='dodgerblue', label='Signals') mp.legend() # 第二步骤 freqs = nf.fftfreq(times.size, 1 / sample_rate) complex_ary = nf.fft(noise_sigs) # 求模,代表能量大小 powers = np.abs(complex_ary) mp.subplot(222) mp.title('Frequent Domain') mp.ylabel('power') mp.grid(linestyle=":") mp.semilogy(freqs[freqs > 0], powers[freqs > 0], c='orangered', label='Noised') mp.legend() # 第三步骤 # 找到频率最大值 fund_freq = freqs[powers.argmax()] # 找出所有噪声下标,where方法返回的是下标数组 nosie_indexes = np.where(freqs != fund_freq) # 拷贝一份,避免修改原始数据 complex_filter = complex_ary.copy() # 将噪声赋值0---滤波 complex_filter[nosie_indexes] = 0 # 求滤波的模大小,代表能量大小 power_filter = np.abs(complex_filter) # 画图 mp.subplot(224) mp.ylabel('power') mp.grid(linestyle=":") mp.plot(freqs[freqs > 0], power_filter[freqs > 0], c='orangered', label='Filter') mp.legend() # 第四步骤 # 根据反向傅里叶,得到过滤后的采样点位移 filter_sigs = nf.ifft(complex_filter).real # 画图 mp.subplot(223) mp.ylabel('Signal') mp.grid(linestyle=':') # 因数据太大,只取前178个 mp.plot(times[:178], filter_sigs[:178], c='dodgerblue', label='Signals') mp.legend() # 第五步骤 # 参数需要,保存路径、采样率、采样位移 wf.write('./da_data/out.wav', sample_rate, filter_sigs.astype('i2')) mp.tight_layout() mp.show()