numpy之数据平滑处理

'''
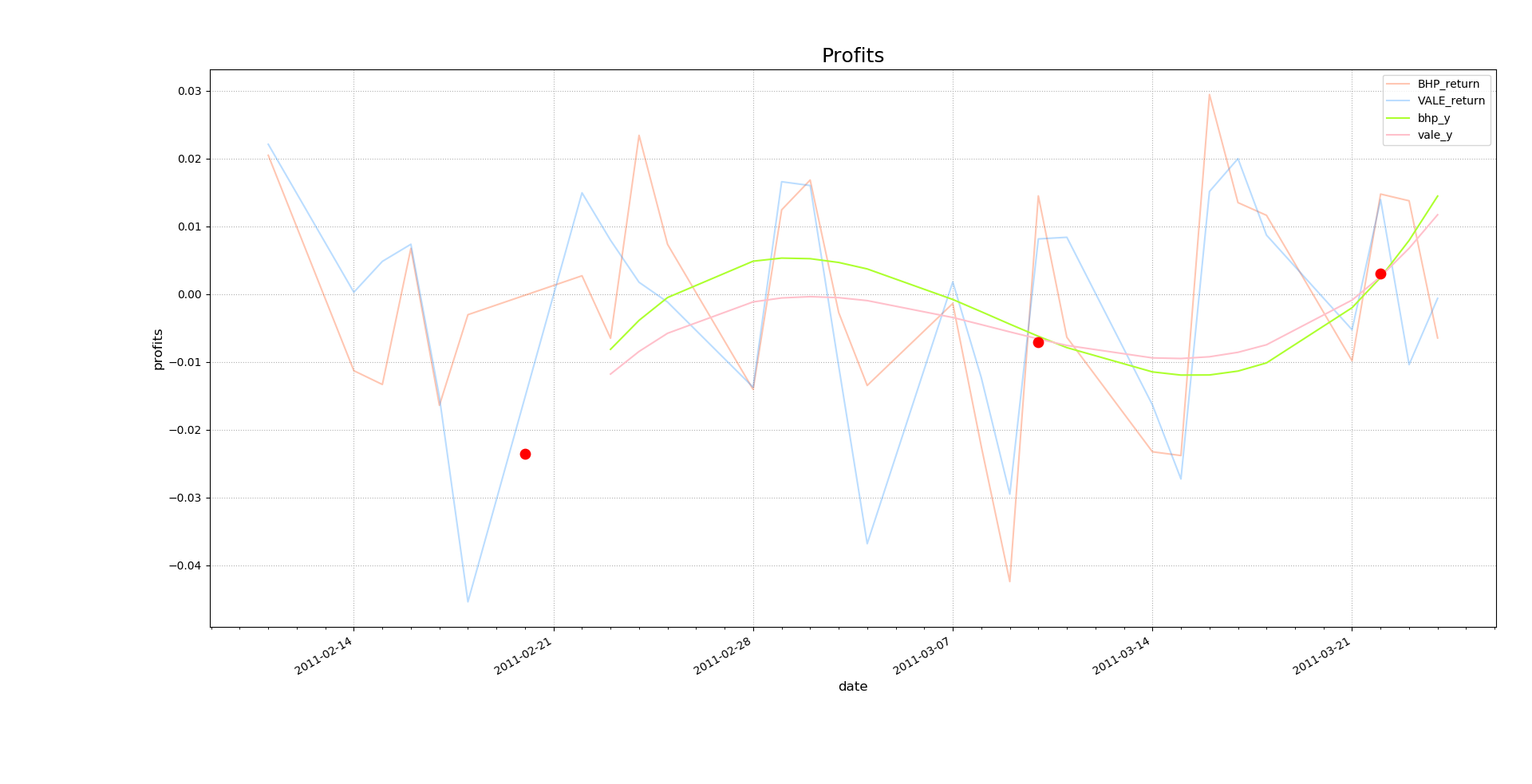
    1.数据平滑：通常包含降噪、拟合等操作。降噪的功能在于去除额外的影响因素，拟合的目的在于数学模型化，可以通过更多的数学方法识别曲线的特征。
    2.绘制两支股票的收益率
                ---收益率 =（后一天的收盘价 - 前一天的收盘价）/前一天的收盘价
'''
import matplotlib.pyplot as mp
import numpy as np
import datetime as dt
import matplotlib.dates as md


# 日期转化函数
def dmy2ymd(dmy):
    # 把dmy格式的字符串转化成ymd格式的字符串
    dmy = str(dmy, encoding='utf-8')
    d = dt.datetime.strptime(dmy, '%d-%m-%Y')
    d = d.date()
    ymd = d.strftime('%Y-%m-%d')
    return ymd


dates, bhp_closing_prices = \
    np.loadtxt('./da_data/bhp.csv', delimiter=',', usecols=(1, 6), unpack=True,
               dtype='M8[D], f8', converters={1: dmy2ymd})  # converters为转换器，运行时先执行，其中1表示时间所在的列索引号

vale_closing_prices = \
    np.loadtxt('./da_data/vale.csv', delimiter=',', usecols=(6,), unpack=True,
               dtype='f8')

# 绘制收盘价折线图
mp.figure('Profits', facecolor='lightgray')
mp.title('Profits', fontsize=18)
mp.xlabel('date', fontsize=12)
mp.ylabel('profits', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 设置x轴的刻度定位器，使之更适合显示日期数据
ax = mp.gca()
# 以周一作为主刻度
ma_loc = md.WeekdayLocator(byweekday=md.MO)
# 次刻度，除周一外的日期
mi_loc = md.DayLocator()
ax.xaxis.set_major_locator(ma_loc)
ax.xaxis.set_major_formatter(md.DateFormatter('%Y-%m-%d'))
ax.xaxis.set_minor_locator(mi_loc)
# 日期数据类型转换，更适合绘图
dates = dates.astype(md.datetime.datetime)
# 计算两支股票的收益率
bhp_returns = np.diff(bhp_closing_prices) / bhp_closing_prices[:-1]
vale_returns = np.diff(vale_closing_prices) / vale_closing_prices[:-1]

# 绘制两支股票的收益率曲线
mp.plot(dates[:-1], bhp_returns, color='orangered', label='BHP_return', alpha=0.3)
mp.plot(dates[:-1], vale_returns, color='dodgerblue', label='VALE_return', alpha=0.3)
# mp.hlines(0, md.date2num(dates[0]), md.date2num(dates[-1]), colors='red')
# 使用卷积对两组数据降噪
kernel = np.hanning(8)  # 随机生成一个卷积核（对称的）
kernel /= kernel.sum()
bhp_returns_convolved = np.convolve(bhp_returns, kernel, 'valid')
vale_returns_convolved = np.convolve(vale_returns, kernel, 'valid')
# mp.plot(dates[7:-1], bhp_returns_convolved, color='orangered', label='bhp_returns_convolved')
# mp.plot(dates[7:-1], vale_returns_convolved, color='dodgerblue', label='vale_returns_convolved')

# 对两条曲线执行多项式拟合
days = dates[7:-1].astype('M8[D]').astype('i4')
bhp_P = np.polyfit(days, bhp_returns_convolved, 3)
vale_P = np.polyfit(days, vale_returns_convolved, 3)
# 绘制多项式曲线
bhp_y = np.polyval(bhp_P, days)
vale_y = np.polyval(vale_P, days)
mp.plot(dates[7:-1], bhp_y, color='greenyellow', label='bhp_y')
mp.plot(dates[7:-1], vale_y, color='pink', label='vale_y')

# 求曲线的交点坐标
P = np.polysub(bhp_P, vale_P)  # 求两个多项式函数的差函数的P值
xs = np.roots(P)
y = np.polyval(bhp_P, xs)
result = xs.astype('i4').astype('M8[D]')
mp.scatter(result, y, s=80, color='red', zorder=3)

mp.tight_layout()
mp.legend()
# 自动格式化x轴日期的显示格式（以最合适的方式显示）
mp.gcf().autofmt_xdate()
mp.show()