yunhantu绘制学习-1-多层网络分析软件介绍

1.pumnet

2.muxViz

3. SATNet

 

---

 

1.  pymnet主页网址：https://mnets.github.io/pymnet/index.html

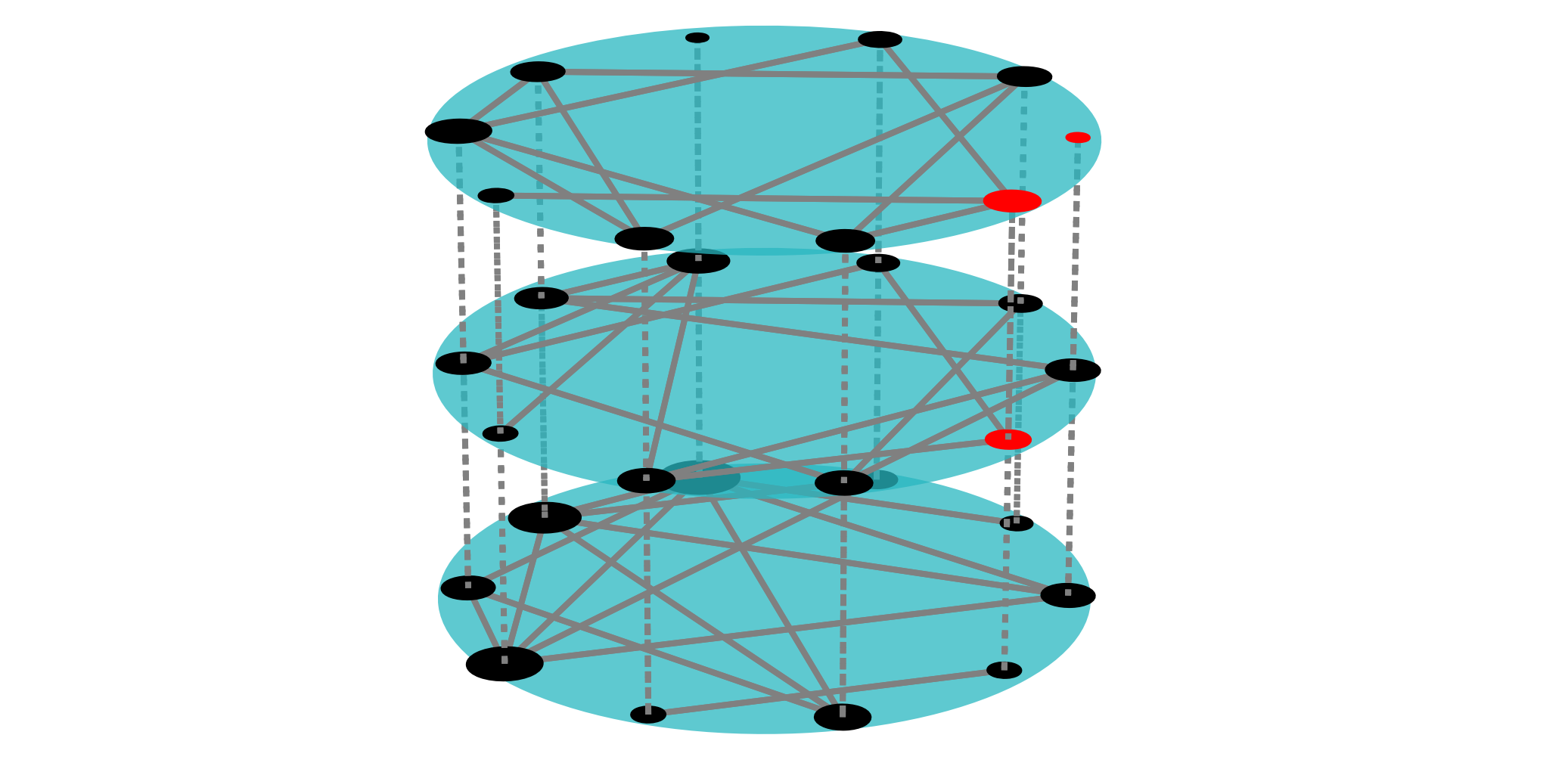
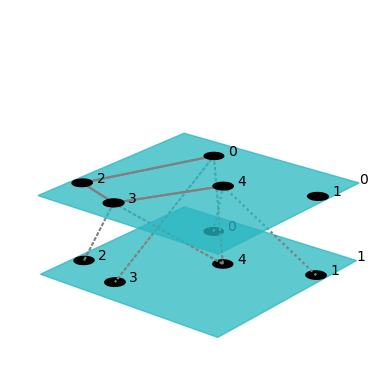
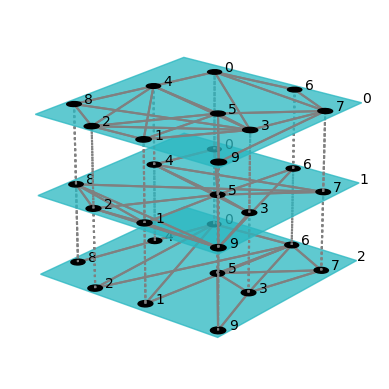
	pymnet模块介绍 The library is based on the general definition of multilayer networks presented in a review article. Multilayer networks can be used to represent various types network generalizations found in the literature. For example, multiplex networks, temporal networks, networks of networks, and interdependent networks are all types of multilayer networks. The library supports even more general types of networks with multiple aspects such that the networks can for example have both temporal and multiplex aspect at the same time. The visualization on the left is produced with the library. See the visualization tutorial for instructions on how to visualize your own network data with the library! 该库基于一篇综述文章中给出的多层网络的一般定义。多层网络可用于表示文献中发现的各种类型的网络概括。例如，多路网络、时间网络、网络的网络和相互依赖的网络都是多层网络的类型。该库甚至支持具有多个方面的更一般类型的网络，使得网络可以例如同时具有时间和复用方面。 左边的可视化是由库产生的。有关如何使用库可视化您自己的网络数据的说明，请参见可视化教程！   Main features include: Pure Python implementation Can handle general multilayer networks Data structures for multilayer networks and multiplex networks Scalable implementation for sparse networks: memory usage scales linearly with the number of edges and number of nodes Rule-based generation and lazy evaluation of coupling edges Various network analysis methods, transformations, reading and writing networks, network models, etc. Visualization (using matplotlib or D3 as a backend) Integration with NetworkX for monoplex network analysis
	关于pymnet库的安装： 引用自：https://bbs.huaweicloud.com/blogs/399360 向原作者致谢！     Github官网：  将下载的文件解压到conda的site-packages目录下：   进入目录: cd D:\python\anaconda\Lib\site-packages\Multilayer-networks-library-master 构建和安装 构建 python setup.py build  继续安装 python setup.py install   安装成功：   导入成功：      初步尝试示例1： from pymnet import * # MultilayerNetwork 是库中的基本网络类——所有其他类型的网络都是它的特例。 # 为了获得单体网络对象，可以简单地构造一个具有 0 个方面的多层网络。 net = MultilayerNetwork(aspects=0) net.add_node(1) net.add_node(2) print(list(net)) print(net[1].deg())    初步尝试示例2： # — coding: utf-8 – from pymnet import * fig3 = draw(er(10, 3 * [0.3]), layout="circular", layershape="circle", nodeColorDict={(0, 0): "r", (1, 0): "r", (0, 1): "r"}, layerLabelRule={}, nodeLabelRule={}, nodeSizeRule={"rule": "degree", "propscale": 0.05}) fig3.savefig("net3.pdf") 我们首先创建了一个三层的空白网络，然后添加了一些层和节点以及它们之间的连接。接下来，我们设置了节点和层的颜色和形状，并使用 pymnet.draw() 函数创建了一个绘图对象。我们使用 lambda 函数将层名称作为标签，并将节点标签设置为 None，这样绘图对象中的节点将不会显示标签。然后，我们使用循环遍历每个节点并设置其形状。最后，我们使用 pymnet.show() 函数显示绘图结果。    在可视化网络时，可以使用 pymnet.draw() 函数的一些参数来设置节点和层的颜色、形状和标签。例如，我们可以使用 nodeColorDict 参数来设置节点颜色字典，使用 layerColorDict 参数来设置层颜色字典，使用 nodeShapeDict 参数来设置节点形状字典，使用 layerLabelRule 参数来设置层标签规则，使用 nodeLabelRule 参数来设置节点标签规则等等。 在 PyMNet 中，还提供了许多其他函数和类，可以用于更高级的多层网络分析和操作，例如层与层之间的投影、多层网络的布局和可视化等等。
	三种类型的网络 Monoplex networks Multilayer networks Multiplex networks Monoplex networks import pymnet net = pymnet.MultilayerNetwork(aspects=0) net.add_node(1) net.add_node(2) net[1, 3] = 1 list(net) #[1, 2, 3] list(net[1]) #the list of neighbors of the node #[2, 3] net[1, 3] = 0 list(net[1]) #[2] #Directed network objects dirnet = pymnet.MultilayerNetwork(aspects=0, directed=True) dirnet[1, 2] = 1 dirnet[1, 2] #1 dirnet[2, 1] #0     Multilayer networks mnet = pymnet.MultilayerNetwork(aspects=1) #In the syntax where you first access a node object and then its neighbor, the order of the indices is different. mnet[1, "a"][2, "b"] = 1 #equivalent to： mnet[1, 2, "a", "b"] = 1 list(mnet[1, "a"]) # [(2, 'b')] list(mnet) # [1, 2] #Sometimes new syntax is needed. For example, the aspect must be specified when adding layers. mnet2.add_layer("c", 1) mnet2.add_layer("z", 2)     Multiplex networks onet = pymnet.MultiplexNetwork(couplings="ordinal") onet.add_node("node") onet.add_layer(1) onet.add_layer(2) onet.add_layer(3) onet["node", "node", 1, 2] cnet = pymnet.MultiplexNetwork(couplings=("categorical", 10)) cnet.add_node(1) cnet.add_layer("a") cnet.add_layer("b") cnet[1, 1, "a", "b"] conet = pymnet.MultiplexNetwork(couplings=["categorical", "ordinal"]) conet.add_node("node") conet.add_layer("a", 1) conet.add_layer("b", 1) conet.add_layer(1, 2) conet.add_layer(2, 2) conet.add_layer(3, 2) conet["node", "node", "a", "a", 1, 2] conet.A[("a", 1)]["node", "node2"] = 1
	Visualizing networks import random random.seed(42) import numpy as np np.random.seed(42) from pymnet import * net = models.er_multilayer(5, 2, 0.2) fig = draw(net) fig.show() fig.savefig("net.pdf")   fig = draw(er(10, 3*[0.4]), layout="spring") fig.show() fig.savefig("net.pdf")   fig = draw(er(10, 3*[0.3]), layout="circular", layershape="circle", nodeColorDict={(0,0):"r", (1,0):"r", (0,1):"r"}, layerLabelRule={}, nodeLabelRule={}, nodeSizeRule={"rule":"degree", "propscale":0.05} )   #If the network is large, then it is often desirable not to plot the coupling edges. Simply create a network without coupling edges and plot it. For example, we can download the Bernard & Killworth fraternity network. import requests dataset = "bkfrat.dat" fraternity_dataset_url = f"http://vlado.fmf.uni-lj.si/pub/networks/data/ucinet/{dataset}" res = requests.get(fraternity_dataset_url) with open(dataset, "wb") as f: f.write(res.content) #This network might then be plotted like this: net = read_ucinet(dataset, couplings="none") net = transforms.threshold(net, 4) fig = draw(net, layout="spring", layerColorRule={}, defaultLayerColor="silver", nodeLabelRule={}, edgeColorRule={"rule":"edgeweight", "colormap":"viridis", "scaleby":0.1}, defaultLayerLabelLoc=(0.9,0.9) )
	Isomorphisms and automorphisms 同构和自同态   要求安装：networkx 和 bliss-blind networkx: Available through pip. Allows the usage of the following functions: is_isomorphic, get_isomorphism. bliss-blind: Installed as a dependency on MacOS, X64 Windows and X64 Linux machines, has to be manually compiled and installed on other system using the command python -m pip install bliss-bind. Allows the usage of the following functions: is_isomorphic, get_isomorphism, get_automorphism_generators, get_complete_invariant.
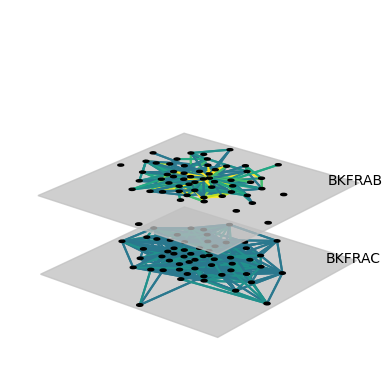
	muxViz MuxViz：多层网络分析与可视化 曼里奥·德·多梅尼科（Manlio De Domenico） 著   相关链接 https://github.com/manlius/muxViz https://github.com/wjj0301/Multiplex-Networks https://groups.google.com/g/muxviz https://link.springer.com/book/10.1007/978-3-030-75718-2 相关博客：介绍了muxViz的安装 https://mp.weixin.qq.com/s?src=11&timestamp=1728434795&ver=5555&signature=b5Gr3YmaEVBenmGxvGTbGoy7iQbbRWJElUntp7W348M2fI8Lmo7SYykavWY*CgB7NRxEM61dMevq0pcA2LGCeMPnLVawi-WQYC3c5zvkGD9cgqwgxvMG4zObNeWVVb1F&new=1   MuxViz：多层网络分析与可视化 作者: 曼里奥·德·多梅尼科 （Manlio.De.Domenico） 出版社:  首都经济贸易大学出版社 出版时间:  2023-08 版次:  1 ISBN:  9787563834860 定价:  58.00 装帧:  其他 开本:  16开 纸张:  胶版纸 页数:  156页 字数:  169千字 内容简介： 多层网络分析方法与可视化技术，是新时代科技文献知识网络分析的新范式，是复杂系统视角下量化科学知识结构及知识元间协同演化的新方法，为科学家洞见知识发展足迹、探寻前进方向插上了智慧的翅膀。本书向读者介绍了多层网络的基本概念、数学模型、动力机制以及基本原理和分析方法，系统讲解了不同类型网络模型中各层的关系以及相应的遍历算法。全书始终以muxViz工具为例，介绍了如何在R中使用该工具构建多层网络并进行相应的分析，以及可视化呈现。以往可视化多集中在单模网络，或叠加网络。该书首次对多层网络的原理、类型、分析方法等进行了系统介绍，在国内同领域书籍中并不多见。 作者简介： ［意］曼里奥·德·多梅尼科（Manlio De Domenico），帕多瓦大学物理和天文学系“伽利略”应用物理学副教授兼复杂多层网络（CoMuNe）实验室负责人。他还是复杂系统学会意大利分会的协调员，也是复杂网络地中海学院的创始董事。他以多层模型而闻名，这些模型交织着人类流动性、传染病传播和其他类型的人类动态，如意识、有限理性、社会隔离和融合。他的研究重点是自然和人工相互依存系统中出现的集体现象，以及对多层网络的多尺度建模和分析，其对结构、动态、信息容量和冲击弹性的研究，在系统生物学、系统医学、计算社会科学、计算流行病学和数据驱动的政策制定中得到了应用。 个人网站: https://manliodedomenico.com/   目录： br/>本书向读者介绍了多层网络的基本概念、数学模型、动力机制以及基本原理和分析方法, 系统介绍了不同类型网络模型中各层的关系以及相应的遍历算法。全书始终以muxViz工具为例, 介绍了如何在R中使用该工具构建多层网络并进行相应的分析, 以及可视化呈现。以往可视化多集中在单模网络, 或叠加网络。该书首次对多层网络的原理、类型、分析方法等进行了系统介绍, 在国内同领域书籍中并不多见。 内容摘要 多层网络分析方法与可视化技术，是新时代科技文献知识网络分析的新范式，是复杂系统视角下量化科学知识结构及知识元间协同演化的新方法，为科学家洞见知识发展足迹、探寻前进方向插上了智慧的翅膀。本书向读者介绍了多层网络的基本概念、数学模型、动力机制以及基本原理和分析方法，系统讲解了不同类型网络模型中各层的关系以及相应的遍历算法。全书始终以muxViz工具为例，介绍了如何在R中使用该工具构建多层网络并进行相应的分析，以及可视化呈现。以往可视化多集中在单模网络，或叠加网络。该书首次对多层网络的原理、类型、分析方法等进行了系统介绍，在国内同领域书籍中并不多见。

 

 

SATNet

https://github.com/locuslab/SATNet

SATNet •    Bridging deep learning and logical reasoning using a differentiable satisfiability solver. This repository contains the source code to reproduce the experiments in the ICML 2019 paper SATNet: Bridging deep learning and logical reasoning using a differentiable satisfiability solver by Po-Wei Wang, Priya L. Donti, Bryan Wilder, and J. Zico Kolter. What is SATNet SATNet is a differentiable (smoothed) maximum satisfiability (MAXSAT) solver that can be integrated into the loop of larger deep learning systems. This (approximate) solver is based upon a fast coordinate descent approach to solving the semidefinite program (SDP) associated with the MAXSAT problem.