本文介绍了符号模型检查算法IC3——SAT应用之一
Nils Froleyks and Armin Biere.
Single Clause Assumption without Activation Literals to Speed-up IC3.
In Proc. 21st Intl. Conf. on Formal Methods in Computer-Aided Design (FMCAD'21), pages 72-76, vol. 2, TU Vienna Academic Press 2021.
|
Abstract: We extend the well-established assumption-based interface of incremental SAT solvers to clauses, allowing the addition of a temporary clause that has the same lifespan as literal assumptions. Our approach is efficient and easy to implement in modern CDCL-based solvers. Compared to previous approaches, it does not come with any memory overhead and does not slow down the solver due to disabled activation literals, thus eliminating the need for algorithms like IC3 to restart the SAT solver. All clauses learned under literal and clause assumptions are safe to keep and not implicitly invalidated for containing an activation literal. These changes increase the quality of learned clauses, resulting in better generalization for IC3.
We implement the extension in the SAT solver CaDiCaL and evaluate it with the IC3 implementation in the model checker ABC. Our experiments on the benchmarks from a recent hardware model checking competition show a speedup for the average SAT call and a reduction in number of calls per verification instance, resulting in a substantial improvement in model checking time. |
|
|
符号模型检查算法IC3 1. 许多应用需要逐步解决一系列相关的SAT问题[2],[3],利用inprocessing技术[4],[5],[6],使现代SAT求解器如此高效。Many applications require solving a sequence of related SAT problems incrementally [2], [3], making use of inprocessing techniques [4], [5], [6] that make modern SAT solvers so efficient. 与其他基于sat的增量技术(如有界模型检查(BMC)[7]、[8]和k-归纳[9]、[10])相比, IC3不依赖于展开转换函数。因此,IC3姿态的SAT查询明显更小,求解速度更快。但是,IC3在一个模型检查过程中进行的查询数量要高得多.
2. We illustrate the kind of queries that IC3 makes in the following example.
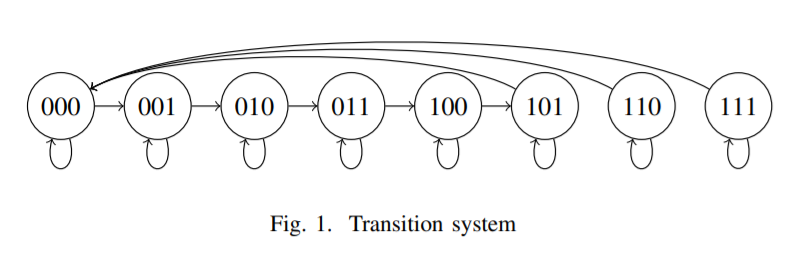
Consider the transition system of a three-bit (b2b1b0) counter, encoding integers up to seven, in Fig. 1. Nondeterministically, the counter is incremented, remains unchanged or is reset to zero after reaching five. 如图1所示,考虑一个3位(b2b1b0)计数器的转换系统,其编码的整数最高可达7。不确定地,计数器将递增、保持不变或在达到5后重置为零。 Suppose we want to ensure that starting at state zero, all states with values greater than five are unreachable. A typical query asks “is state six reachable from any other state?”, expressed as SAT? 假设我们要确保从状态0开始,所有值大于5的状态都不可达。典型的查询是“状态6是否可以从任何其他状态访问?”,表示为SAT?
The popular assumption-based interface pioneered by MiniSat [2], [8] allows the user to specify a set of literals that are assumed to be true and picked by the solver as the first decisions. 流行的基于假设的界面由MiniSat[2],[8]允许用户指定一组文本,这些文本被假设为真,并由求解器选择作为第一个决策。
This allows us to add the assumption that a state is within a certain cube after the transition (b'2Λb'1). however we still need to assume an additional clause encoding that the state is currently not within said cube (¬b2ν¬b1). 这允许我们添加一个假设,即状态在转换之后位于某个多维数据集中(b'2Λb'1)。 然而,我们仍然需要假设一个额外的子句编码,即状态当前不在上述多维数据集(¬b2ν¬b1)内。
The most common way to implement clause assumption, is to simulate the desired behavior using activation literals [8], [11]. 实现子句假设最常见的方法是使用激活字面量模拟期望的行为[8],[11]。 Let C be a clause to add temporarily and a, the activation literal, a free variable, i.e., it does not occur in the formula. 设C是临时添加的子句,而a是激活文字,是一个自由变量,也就是说,它不会出现在公式中。 By adding C ∨a to the formula and assuming ¬a, we achieve the same as adding C to the formula. After a solution is found, the clause a is added, effectively removing C from the formula. 对对地在公式中加入C ∨a,假设¬a,得到与在公式中加入C相同的结果。找到解后,加入a项,有效地将C从公式中去掉。
3. The problem with IC3 specifically, is the large number of queries made over the course of a single verification procedure. After a few hundred calls the activation literals clutter up the variable space and slow down the SAT solvers propagation. 具体来说,IC3的问题是在单个验证过程中进行了大量查询。在几百次调用之后,激活字面量会使变量空间变得混乱,并减慢SAT求解器的传播速度。 The common solution to this problem is to fully restart the SAT solver by replacing it with a fresh instance periodically, thus also deleting all learned clauses and heuristic scores. 这个问题的常见解决方案是通过定期用一个新的实例替换它来完全重新启动SAT求解器,从而删除所有学过的子句和启发式分数。
4. How to schedule these restarts in IC3 specifically, has been the topic of a full journal paper [12]. 如何在IC3中具体安排这些重启,一直是一篇完整期刊论文的主题[12]。 Using the technique presented in this paper, restarts are not necessary at all. Additionally learned clauses are safe to keep and will not contain an activation literal, which would make them useless for future calls. 使用本文提出的技术,根本不需要重新启动。此外,学习的子句可以安全保存,并且不会包含激活文字,这将使它们对将来的调用毫无用处。 |
|
|
Other approaches to clause assumption have been explored: The logic solver Satire [13] supports pseudo-Boolean and other constraints. It records the dependencies of learned constraints explicitly, thus allowing the deletion of arbitrary clauses. In the SMT community, an interface based on pushing and popping on the assertion stack is prevalent [14]. 其他的子句假设方法也被探索过:逻辑求解器sarcasm[13]支持伪布尔约束和其他约束。它明确地记录学习约束的依赖关系,从而允许删除任意子句。在SMT社区中,基于断言堆栈上的推送和弹出的接口很流行[14]。 Since constraints are removed in order, it is possible to mark a point in the data structures that maintain learned knowledge and remove everything past it, when a pop operation is executed. 由于约束是按顺序删除的,因此在执行pop操作时,可以在数据结构中标记一个点来维护已学习的知识,并删除它后面的所有内容。 The first implementation of IC3 [15] used the SAT solver Zchaff [16]. It assigns an additional 32-bit integer to each clause. When learning a clause the bits of all dependencies are combined. The user can delete a group of clauses with a certain bit. This approach mostly simulates the use of activation literals and comes with a significant memory overhead. IC3的第一次实现[15]使用了SAT求解器Zchaff[16]。它为每个子句分配一个额外的32位整数。当学习一个子句时,所有依赖项的位被组合在一起。用户可以删除一组具有特定位的子句。这种方法主要模拟激活字面量的使用,并带来了很大的内存开销。 |
|
|
This paper presents an extension of the prevalent assumption mechanism to additionally allow the assumption of a single clause, called constraint in the following. The extension can be implemented by a simple modification to the decision mechanism in a CDCL-based SAT solver. 本文提出了一种普遍假设机制的扩展,以额外允许对单个子句的假设,在下面称为约束。该扩展可以通过对基于cdcl的SAT求解器中的决策机制进行简单修改来实现。 We implemented it in under 100 lines of code in the state-of-the-art SAT solver CaDiCaL. To evaluate our implementation we modify the IC3 engine in the model checker ABC to use CaDiCaL and clause assumption. 我们在最先进的SAT求解器CaDiCaL中用不到100行代码实现了它。为了评估我们的实现,我们修改了模型检查器ABC中的IC3引擎,以使用CaDiCaL和子句假设。 As a first result, the changes simplify SAT solver usage and eliminate the need for restarts as well as some bookkeeping for activation literals. 首先,这些更改简化了SAT求解器的使用,消除了重新启动的需要以及激活文本的一些记录。 An empirical evaluation on the 2019 hardware model checking competition [17] benchmark set shows that ABC spends less time outside of computing SAT queries, the number of queries per verification is reduced and the average SAT call is faster. Overall using clause assumptions yields a substantial speedup in verification time. 对2019年硬件模型检查竞争[17]基准集的实证评估表明,ABC在计算SAT查询之外花费的时间更少,每次验证的查询数量减少,平均SAT调用速度更快。总的来说,使用子句假设可以大大加快验证时间。 |
|
|
REFERENCES [1] Marques-Silva, Joao and Lynce, Ines and Malik, Sharad, “Chapter 4. Conflict-Driven Clause Learning SAT Solvers,” in Handbook of Satisfiability: Second Edition, Biere, Armin and Heule, Marijn and van Maaren, Hans and Walsh, Toby, Ed. IOS Press, feb 2021. [2] Eén, Niklas and Sörensson, Niklas, “An Extensible SAT-Solver,” in Theory and Applications of Satisfiability Testing, ser. Lecture Notes in Computer Science, Giunchiglia, Enrico and Tacchella, Armando, Ed. Berlin, Heidelberg: Springer, 2004, pp. 502–518. [3] Audemard, Gilles and Lagniez, Jean-Marie and Simon, Laurent, “Improving Glucose for Incremental SAT Solving with Assumptions,” in Theory and Applications of Satisfiability Testing – SAT 2013, ser. Lecture Notes in Computer Science, Järvisalo, Matti and Van Gelder, Allen, Ed. Berlin, Heidelberg: Springer, 2013, pp. 309–317. [4] Eén, Niklas and Biere, Armin, “Effective Preprocessing in SAT Through Variable and Clause Elimination,” in Theory and Applications of Satisfiability Testing, ser. Lecture Notes in Computer Science, Bacchus, Fahiem and Walsh, Toby, Ed. Berlin, Heidelberg: Springer, 2005, pp. 61–75. [5] Järvisalo, Matti and Heule, Marijn J. H. and Biere, Armin, “Inprocessing Rules,” in Automated Reasoning, ser. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 2012, pp. 355–370. [6] Fazekas, Katalin and Biere, Armin and Scholl, Christoph, “Incremental Inprocessing in SAT Solving,” in Theory and Applications of Satisfiability Testing – SAT 2019, ser. Lecture Notes in Computer Science, Janota, Mikoláš and Lynce, Inês, Ed. Cham: Springer International Publishing, 2019, pp. 136–154. [7] Biere, Armin and Cimatti, Alessandro and Clarke, Edmund and Zhu, Yunshan, “Symbolic Model Checking without BDDs,” in Tools and Algorithms for the Construction and Analysis of Systems, ser. Lecture Notes in Computer Science, Cleaveland, W. Rance, Ed. Berlin, Heidelberg: Springer, 1999, pp. 193–207. [8] Eén, Niklas and Sörensson, Niklas, “Temporal Induction by Incremental SAT Solving,” Electronic Notes in Theoretical Computer Science, vol. 89, no. 4, pp. 543–560, jan 2003. [9] Bjesse, Per and Claessen, Koen, “SAT-Based Verification without State Space Traversal,” in Formal Methods in Computer-Aided Design, ser. Lecture Notes in Computer Science, Hunt, Warren A. and Johnson, Steven D., Ed. Berlin, Heidelberg: Springer, 2000, pp. 409–426. [10] Sheeran, Mary and Singh, Satnam and Stålmarck, Gunnar, “Checking Safety Properties Using Induction and a SAT-Solver,” in Formal Methods in Computer-Aided Design, ser. Lecture Notes in Computer Science, Hunt, Warren A. and Johnson, Steven D., Ed. Berlin, Heidelberg: Springer, 2000, pp. 127–144. [11] Balyo, Tomáš and Biere, Armin and Iser, Markus and Sinz, Carsten, “SAT Race 2015,” Artificial Intelligence, vol. 241, pp. 45–65, dec 2016. [12] Cabodi, G. and Camurati, P. E. and Mishchenko, A. and Palena, M. and Pasini, P., “SAT Solver Management Strategies in IC3: An Experimental Approach,” Formal Methods in System Design, vol. 50, pp. 39–74, mar 2017. [13] Whittemore, J. and Kim, J. and Sakallah, K., “SATIRE: A New Incremental Satisfiability Engine,” in Proceedings of the 38th Design Automation Conference (IEEE Cat. No.01CH37232), jun 2001, pp. 542– 545. [14] Barrett, Clark and Stump, Aaron and Tinelli, Cesare and others, “The Smt-Lib Standard: Version 2.0,” in Proceedings of the 8th International Workshop on Satisfiability modulo Theories (Edinburgh, England), vol. 13, 2010, p. 14. [15] Bradley, Aaron R., “SAT-Based Model Checking without Unrolling,” in Verification, Model Checking, and Abstract Interpretation, ser. Lecture Notes in Computer Science, Jhala, Ranjit and Schmidt, David, Ed. Berlin, Heidelberg: Springer, 2011, pp. 70–87. [16] Fu, Zhaohui and Marhajan, Yogesh and Malik, Sharad, “Zchaff Sat Solver,” 2004. [17] Preiner, Mathias and Biere, Armin, “Hardware Model Checking Competition 2019,” http://fmv.jku.at/hwmcc19/, 2019. [18] Van Gelder, Allen, “Autarky Pruning in Propositional Model Elimination Reduces Failure Redundancy,” Journal of Automated Reasoning, vol. 23, no. 2, pp. 137–193, aug 1999. |
|