非时序回溯与时序回溯代码分析（2023-9-1复习）

 

参考文献

[1] Alexander Nadel, Vadim Ryvchin:

Chronological Backtracking. SAT 2018: 111-121 

[2] Sibylle Möhle, Armin Biere:

Combining Conflict-Driven Clause Learning and Chronological Backtracking for Propositional Model Counting. GCAI 2019: 113-126 

[3] Hickey R., Bacchus F. (2020) Trail Saving on Backtrack. In: Pulina L., Seidl M. (eds) Theory and Applications of Satisfiability Testing – SAT 2020. SAT 2020. Lecture Notes in Computer Science, vol 12178. Springer, Cham. https://doi.org/10.1007/978-3-030-51825-7_4

 

求解器源码：Relaxed_LCMDCBDL_newTech

代码分析：

 

初始设置值：

    chrono, "Controls if to perform chrono backtrack", 100；
    conf_to_chrono, "Controls number of conflicts to perform chrono backtrack", 4000;

过程统计量：

    chrono_backtrack

    non_chrono_backtrack
   
 

search函数中关于非时序与时序的分支条件判断

// check chrono backtrack condition
if (   (confl_to_chrono < 0 || confl_to_chrono <= conflicts)     && chrono > -1    &&   (decisionLevel() - backtrack_level) >= chrono    )
{
++chrono_backtrack;
cancelUntil(data.nHighestLevel -1);
}
else // default behavior
{
++non_chrono_backtrack;
cancelUntil(backtrack_level);
}

解读：

（1）默认为非时序回溯；如果初始选项设置chrono为小于-1的值，则不会发生时序回溯；

（2）冲突数大于confl_to_chrono=4000，且chrono设置大于-1，则发生时序回溯主要取决于第三个条件回溯的层数跨度大于chrono=100；

可以看出，回溯跨度太大采用时序回溯可以提高求解性能。所谓“太大”选取100应该是一个实验得到的经验值。

 
   
 

 非时序回溯切换到时序回溯的原因分析文献中的表述：

可以看出，回溯跨度太大采用时序回溯可以提高求解性能。所谓“太大”选取100应该是一个实验得到的经验值。
   
 

 相关代码1：

//solver.h

 1 struct ConflictData
 2 {
 3     ConflictData() :
 4         nHighestLevel(-1),
 5         bOnlyOneLitFromHighest(false)    //注意此处默认为false
 6         {}
 7 
 8     int nHighestLevel;
 9     bool bOnlyOneLitFromHighest;
10 };

ConflictData FindConflictLevel(CRef cind); 

 

//solver.cpp

 1 inline Solver::ConflictData Solver::FindConflictLevel(CRef cind)
 2 {
 3     ConflictData data;
 4     Clause& conflCls = ca[cind];
 5     data.nHighestLevel = level(var(conflCls[0]));
 6     if (data.nHighestLevel == decisionLevel() && level(var(conflCls[1])) == decisionLevel())
 7     {
 8         return data;
 9     }
10 
11     int highestId = 0;
12     data.bOnlyOneLitFromHighest = true;
13     // find the largest decision level in the clause
14     for (int nLitId = 1; nLitId < conflCls.size(); ++nLitId)
15     {
16         int nLevel = level(var(conflCls[nLitId]));
17         if (nLevel > data.nHighestLevel)
18         {
19             highestId = nLitId;
20             data.nHighestLevel = nLevel;
21             data.bOnlyOneLitFromHighest = true;
22         }
23         else if (nLevel == data.nHighestLevel && data.bOnlyOneLitFromHighest == true)
24         {
25             data.bOnlyOneLitFromHighest = false;
26         }
27     }
28 
29     if (highestId != 0)
30     {
31         std::swap(conflCls[0], conflCls[highestId]);
32         if (highestId > 1)
33         {
34             OccLists<Lit, vec<Watcher>, WatcherDeleted>& ws = conflCls.size() == 2 ? watches_bin : watches;
35             //ws.smudge(~conflCls[highestId]);
36             remove(ws[~conflCls[highestId]], Watcher(cind, conflCls[1]));
37             ws[~conflCls[0]].push(Watcher(cind, conflCls[1]));
38         }
39     }
40 
41     return data;
42 }

 

 1 //search函数中发生冲突代码段
 2 
 3 。。。
 4         ConflictData data = FindConflictLevel(confl);
 5         if (data.nHighestLevel == 0) {
 6             return l_False;
 7         }
 8 
 9         if (data.bOnlyOneLitFromHighest)//冲突发生在冲突层的决策文字（或隐含决策文字）本身观察中的两个子句之间
10         {
11             cancelUntil(data.nHighestLevel - 1);
12             continue;
13         }
14 
15         learnt_clause.clear();
16         if(DISTANCE) {
17             collectFirstUIP(confl);
18         }
19 
20         analyze(confl, learnt_clause, backtrack_level, lbd);
21         // check chrono backtrack condition
22         if (  (confl_to_chrono < 0 || confl_to_chrono <= conflicts) 
                   && chrono > -1 
                   && (decisionLevel() - backtrack_level) >= chrono        )
23         {
24             ++chrono_backtrack;
25             cancelUntil(data.nHighestLevel -1); //回溯至决策层减一层
26         }
27         else // default behavior
28         {
29             ++non_chrono_backtrack;
30             cancelUntil(backtrack_level);
31         }
32 
33         lbd--;
34 。。。

 

 从以上代码分析可知：

（1）时序回溯发生在两种情形：　　

    data.bOnlyOneLitFromHighest为真和回溯跨度大于等于chrono。

（2）以上代码对回溯的时序与非时序做出明确的决定。

（3）关于非时序回溯的回溯层backtrack_level的取得以及取得过程冲发生了哪些故事需要继续查看

analyze(confl, learnt_clause, backtrack_level, lbd)函数的代码。

 
   
 

 //solver.cpp中分析函数代码解读

void Solver::analyze(CRef confl, vec<Lit>& out_learnt, int& out_btlevel, int& out_lbd)代码片段：

 //生成学习子句

 1     // Generate conflict clause:
 2     //
 3     out_learnt.push();      // (leave room for the asserting literal)
 4     int index   = trail.size() - 1;
 5     int nDecisionLevel = level(var(ca[confl][0]));
 6     assert(nDecisionLevel == level(var(ca[confl][0])));
 7 
 8     do{
 9         assert(confl != CRef_Undef); // (otherwise should be UIP)
10         Clause& c = ca[confl];
11 
12         // For binary clauses, we don't rearrange literals in propagate(), 
13         // so check and make sure the first is an implied lit.
14         if (p != lit_Undef && c.size() == 2 && value(c[0]) == l_False){
15             assert(value(c[1]) == l_True);
16             Lit tmp = c[0];
17             c[0] = c[1], c[1] = tmp; }
18 
19         // Update LBD if improved.        
20 
21         for (int j = (p == lit_Undef) ? 0 : 1; j < c.size(); j++){
22             Lit q = c[j];            
23 
24             if (!seen[var(q)] && level(var(q)) > 0){
25                 if (VSIDS){
26                     varBumpActivity(var(q), .5);
27                     add_tmp.push(q);
28                 }else
29                     conflicted[var(q)]++;

30                 seen[var(q)] = 1;

31                 if (level(var(q)) >= nDecisionLevel){
32                     pathC++;
33                 }else
34                     out_learnt.push(q);
35             }        
36         }
37         
38         // Select next clause to look at:
39         do {
40             while (!seen[var(trail[index--])]);
41             p  = trail[index+1];
42         } while (level(var(p)) < nDecisionLevel);
43         
44         confl = reason(var(p));
45         seen[var(p)] = 0;
46         pathC--;
47 
48     }while (pathC > 0);
49     out_learnt[0] = ~p;

 

//得到回溯层

 1 // Find correct backtrack level:
 2     //
 3     if (out_learnt.size() == 1)
 4         out_btlevel = 0;
 5     else{
 6         int max_i = 1;
 7         // Find the first literal assigned at the next-highest level:
 8         for (int i = 2; i < out_learnt.size(); i++)
 9             if (level(var(out_learnt[i])) > level(var(out_learnt[max_i])))
10                 max_i = i;
11         // Swap-in this literal at index 1:
12         Lit p             = out_learnt[max_i];
13         out_learnt[max_i] = out_learnt[1];
14         out_learnt[1]     = p;              //学习子句中次大层文字放在1标号位置
15         out_btlevel       = level(var(p));
16     }

 

//计算学习子句LBD

 1     template<class V> 
 2     int computeLBD(const V& c) {
 3         int lbd = 0;
 4 
 5         counter++;
 6         for (int i = 0; i < c.size(); i++){
 7             int l = level(var(c[i]));
 8             if (l != 0 && seen2[l] != counter){
 9                 seen2[l] = counter;
10                 lbd++; } }
11 
12         return lbd;
13     }

 

//学习子句生成后开始化简代码段开始，求解器数据成员analyze_toclear在以下几个函数中始终起作用且被用到，直至下一次冲突分析时调用充值并更新（代码：out_learnt.copyTo(analyze_toclear);）

//化简子句时用到 litRedundant函数

 1 // Check if 'p' can be removed. 'abstract_levels' is used to abort early if the algorithm is
 2 // visiting literals at levels that cannot be removed later.
 3 bool Solver::litRedundant(Lit p, uint32_t abstract_levels)
 4 {
 5     analyze_stack.clear(); analyze_stack.push(p);
 6     int top = analyze_toclear.size();
 7     while (analyze_stack.size() > 0){
 8         assert(reason(var(analyze_stack.last())) != CRef_Undef);
 9         Clause& c = ca[reason(var(analyze_stack.last()))]; analyze_stack.pop();
10 
11         // Special handling for binary clauses like in 'analyze()'.
12         if (c.size() == 2 && value(c[0]) == l_False){
13             assert(value(c[1]) == l_True);
14             Lit tmp = c[0];
15             c[0] = c[1], c[1] = tmp; }
16 
17         for (int i = 1; i < c.size(); i++){
18             Lit p  = c[i];
19             if (!seen[var(p)] && level(var(p)) > 0){
20                 if (reason(var(p)) != CRef_Undef && (abstractLevel(var(p)) & abstract_levels) != 0){
21                     seen[var(p)] = 1;
22                     analyze_stack.push(p);
23                     analyze_toclear.push(p);
24                 }else{
25                     for (int j = top; j < analyze_toclear.size(); j++)
26                         seen[var(analyze_toclear[j])] = 0;
27                     analyze_toclear.shrink(analyze_toclear.size() - top);
28                     return false;
29                 }
30             }
31         }
32     }
33 
34     return true;
35 }

 

//化简子句时用到binResMinimize函数

// Try further learnt clause minimization by means of binary clause resolution.
bool Solver::binResMinimize(vec<Lit>& out_learnt)
{
    // Preparation: remember which false variables we have in 'out_learnt'.
    counter++;
    for (int i = 1; i < out_learnt.size(); i++)
        seen2[var(out_learnt[i])] = counter;

    // Get the list of binary clauses containing 'out_learnt[0]'.
    const vec<Watcher>& ws = watches_bin[~out_learnt[0]];

    int to_remove = 0;
    for (int i = 0; i < ws.size(); i++){
        Lit the_other = ws[i].blocker;
        // Does 'the_other' appear negatively in 'out_learnt'?
        if (seen2[var(the_other)] == counter && value(the_other) == l_True){
            to_remove++;
            seen2[var(the_other)] = counter - 1; // Remember to remove this variable.
        }
    }

    // Shrink.
    if (to_remove > 0){
        int last = out_learnt.size() - 1;
        for (int i = 1; i < out_learnt.size() - to_remove; i++)
            if (seen2[var(out_learnt[i])] != counter)
                out_learnt[i--] = out_learnt[last--];
        out_learnt.shrink(to_remove);
    }
    return to_remove != 0;
}

//其中使用到求解器数据成员计数器counter和向量seen2
   
 

 回溯函数的解读

（1）回溯的距离：

从for (int c = trail.size()-1; c >= trail_lim[bLevel]; c--)可知，位置大于等于bLevel文字均被释放了；bLevel是即层bLevel+1层的起始点，即回溯至回溯层bLevel的尾部；

（2）回溯过程中实现了以下功能：

       i.使用add_tmp.收集（注意是按在trail中存在位置的倒序收集）被回溯的各层中的一些特殊文字——文字对应所在层属性值小于bLevel；

       ii.实现被回溯各层中非特殊文字的activity_CHB[x]活跃度更新——采用？方法。注意：实际上如果没有参与冲突阶段的相关工作（直接或间接存在于蕴含图路径上），是不应该更新的。

      iii. 撤销文字赋值同时当相位保持技术选项为真时记录原有相位。

（3）函数后部还将收集到的特殊文字（add_tem集合）按当前顺序放如入bLevel层；

（4）最后将qhead设置在现有复制队列所有文字的尾部。

 1 // Revert to the state at given bLevel (keeping all assignment at 'bLevel' but not beyond).
 2 //
 3 void Solver::cancelUntil(int bLevel) {
 4     
 5     if (decisionLevel() > bLevel){
 6 #ifdef PRINT_OUT
 7         std::cout << "bt " << bLevel << "\n";
 8 #endif                
 9         add_tmp.clear();
10         for (int c = trail.size()-1; c >= trail_lim[bLevel]; c--)
11         {
12             Var      x  = var(trail[c]);
13 
14             if (level(x) <= bLevel)
15             {
16                 add_tmp.push(trail[c]);
17             }
18             else
19             {
20                  if (!VSIDS){
21                     uint32_t age = conflicts - picked[x];
22                     if (age > 0){
23                         double adjusted_reward 
                                       = ((double) (conflicted[x] + almost_conflicted[x])) / ((double) age);
24                         double old_activity = activity_CHB[x];
25                         activity_CHB[x] = step_size * adjusted_reward + ((1 - step_size) * old_activity);
26                         if (order_heap_CHB.inHeap(x)){
27                             if (activity_CHB[x] > old_activity)
28                                 order_heap_CHB.decrease(x);
29                             else
30                                 order_heap_CHB.increase(x);
31                         }
32                     }
33 #ifdef ANTI_EXPLORATION
34                     canceled[x] = conflicts;
35 #endif
36                 }
37                 
38                 assigns [x] = l_Undef;
39 #ifdef PRINT_OUT
40                 std::cout << "undo " << x << "\n";
41 #endif                
42                 if (phase_saving > 1 || (phase_saving == 1) && c > trail_lim.last())
43                     polarity[x] = sign(trail[c]);
44                 insertVarOrder(x);
45             }
46         }
47         qhead = trail_lim[bLevel];
48         trail.shrink(trail.size() - trail_lim[bLevel]);
49         trail_lim.shrink(trail_lim.size() - bLevel);
50         for (int nLitId = add_tmp.size() - 1; nLitId >= 0; --nLitId)
51         {
52             trail.push_(add_tmp[nLitId]);
53             curSecarchCancelUntil_add_tmp_LitNum++;          
64 
65         }
66 
67 
68         if(bLevel<1){
69             indexBack0LevelTrail = trail.size() ;71   
72         }
73         
74         add_tmp.clear();
75     } 
76 }

 
    
1 //赋值序列文字入队函数默认0层及所在来源子句为CRef_Undef
2 
3 //solver.h
4 void     uncheckedEnqueue (Lit p, int level = 0, CRef from = CRef_Undef);
//solver.cc中两个函数

CRef Solver::propagateLits(vec<Lit>& lits) {
    Lit lit;
    int i;

    for(i=lits.size()-1; i>=0; i--) {
        lit=lits[i];
        if (value(lit) == l_Undef) {
            newDecisionLevel();
            uncheckedEnqueue(lit);
            CRef confl = propagate();
            if (confl != CRef_Undef) {
                return confl;
            }
        }
    }
    return CRef_Undef;
}

//search函数中有以下代码段
 。。。

           if (learnt_clause.size() == 1){
                uncheckedEnqueue(learnt_clause[0]);
            }
。。。
           // Increase decision level and enqueue 'next'
            newDecisionLevel();
            uncheckedEnqueue(next, decisionLevel());

。。。。

 
   

 

相关文献阅读笔记：

 

   

Alexander Nadel, Vadim Ryvchin:

Chronological Backtracking. SAT 2018: 111-121 

 

NCB–Chronological Backtracking (CB)–in a modern SAT solver

 

Implementing CB is a non-trivial task as it changes some of the indisputable invariants of modern SAT solving algorithms.

译文：实现CB是一项不平凡的任务，因为它改变了现代SAT求解算法的一些无可争议的不变量。
 

早期求解说明时用到的术语与现在略有不同：

    conflicting clause 指的是BCP遇到的冲突所对应的按现有trail中变元序列赋值排查到的文字全为假的子句。

    conflict clause   指的是学习得到的子句，近期文献称learnt clause。
 

 对CDCL回溯讲的比较简介明了：

 
 

NCB’s predecessor is conflict-directed backjumping, proposed in the context of the Constraint Satisfaction Problem (CSP) [11].

The idea behind NCB is to improve the solver’s locality by removing variables irrelevant for conflict analysis from the assignment trail.

NCB的前身是冲突导向回溯，是在约束满足问题(CSP)的背景下提出的。NCB背后的思想是通过从分配轨迹中删除与冲突分析无关的变量来提高求解器的局部性。
   

译文：设时序回溯(CB)是一种回溯算法，它总是回溯到冲突决策层cl之前的决策层(即在CB中，bl = cl−1)。在我们提出的实现中执行CB, v被翻转并传播(与NCB情况完全相同)，然后求解器继续进行下一个决策或继续冲突分析循环。

 
   

In particular, the decision level of the variables in the assignment trail is no longer monotonously increasing. Moreover, the solver may learn a conflict clause whose highest decision level is higher than the current decision level. 

译文：特别是，赋值轨迹中变量的决策水平不再单调递增。此外，求解器可能会学习到一个最高决策级别高于当前决策级别的冲突子句。—— 如何理解？代码中为什么已经考虑了这种情况？—— 下面文献中给出实列彩图给出了解释。
 

 作者认为NCB的缺点是：

    （1） 应用NCB可能确实会导致无用的回溯(不一定要回溯到决策级别0)和几乎相同字面量的重新分配。举得一个例子，将冲突生成学习子句是单文字的C，需要回溯到0层，由于C和前面10^7个变元的传播没有关系，所以此次回溯实践中是无用的。

In standard backtracking, the difference between the backtrack level, Lback and the current deepest level Ldeep can be very large. During its new descent from Lback the solver can reproduce a large number of the same decisions and unit propagations, essentially wasting work.

   （2）此外，NCB过于激进:它可能仅仅因为对最新的冲突解决没有贡献，就把好的决策从回溯中删除。——对此文章中并没有展开。

原文截图如下：

 
 

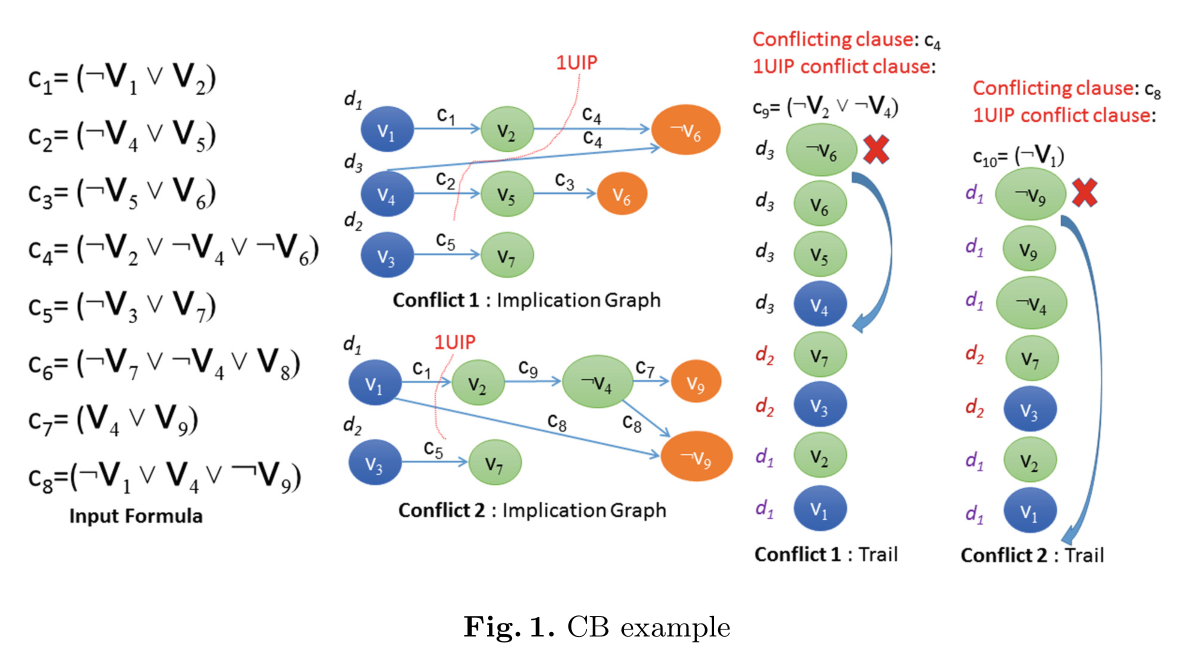
 作者在第二部分给出了时序回溯的详细讲解——图文如下：（可作为DPLL的实力来演示）

 该实例图解给出了trail中文字不是按层分布，即赋值轨迹中变量的决策水平不再单调递增。主要是回溯层数是按照学习子句的次大层来定义的。

 

疑问：第一次冲突发生后，时序回溯v4反转取值后加入trail，为什么不保留原来的层号d3？trail和trail_lim中数据是如何保留的？

 

解答：由于时序回溯回到了当前层的下一层（data.nHighestLevel -1层）；但是唯一蕴含点变元赋值反转后，是按照以下语句进入到传播队列之中，

uncheckedEnqueue(learnt_clause[0], backtrack_level, cr);

也就是说qhead指向的排查文字是带着backtrack_level层信息进入到data.nHighestLevel -1层中的。

 

思考：时序回溯为什么不直接另起一层？这样混在较高层中有什么好处？

 
 

 作者给出了NCB与CB相结合的CDCL框架：——自2018年之后被最新求解器广泛采用。

 注：

（1）该框架流程略去了重启、学习子句集管理、化简等模块所在环节。

（2）bl采用ncb还是cb，取决于user-given threshold T；T是一个经验值。

 

附上文献给出的子模块流程图如下：

 

 
 

 文献通过实验证实非时序与时序回溯结合的优势：

（1）能求出更多的样例；

（2）In addition, Maple LCM Dist becomes consistently faster on unsatisfiable instances。

 

文献结论原文Conclusion

We have shown how to implement Chronological Backtracking (CB) in a modern SAT solver as an alternative to Non-Chronological Backtracking (NCB),which has been commonly used for over two decades.

We have integrated CB into the winner of the SAT Competition 2017, Maple LCM Dist, and the winner of MaxSAT Evaluation 2017 Open-WBO. CB improves the overall performance of both solvers. In addition, Maple LCM Dist becomes consistently faster on unsatisfiable instances, while Open-WBO solves 10 families significantly faster.
   
   

Notes

  1. 1.

    In the standard algorithm, cl is always equal to the current decision level, but, as we shall see, that is not the case for CB.

References

  1. Ansotegui, C., Bacchus, F., Järvisalo, M., Martins, R. (eds.): MaxSAT evaluation 2017: solver and benchmark descriptions, Department of Computer Science Series of Publications B. University of Helsinki, vol. B-2017-2 (2017)

    Google Scholar 

  2. Biere, A., Heule, M., van Maaren, H., Walsh, T. (eds.): Handbook of Satisfiability, Volume 185 of Frontiers in Artificial Intelligence and Applications. IOS Press, Amsterdam (2009)

    Google Scholar 

  3. Eén, N., Sörensson, N.: An extensible SAT-solver. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 502–518. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24605-3_37

    CrossRef Google Scholar 

  4. Frost, D., Dechter, R.: In search of the best constraint satisfaction search. In: AAAI, pp. 301–306 (1994)

    Google Scholar 

  5. Heule, M., Järvisalo, M., Balyo, T.: SAT competition (2017). https://baldur.iti.kit.edu/sat-competition-2017/

  6. Katebi, H., Sakallah, K.A., Marques-Silva, J.P.: Empirical study of the anatomy of modern SAT solvers. In: Sakallah, K.A., Simon, L. (eds.) SAT 2011. LNCS, vol. 6695, pp. 343–356. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21581-0_27

    CrossRef MATH Google Scholar 

  7. Luo, M., Li, C.-M., Xiao, F., Manyà, F., Lü, Z.: An effective learnt clause minimization approach for CDCL SAT solvers. In: Sierra, C. (ed.), Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence IJCAI 2017, Melbourne, Australia, 19–25 August 2017, pp. 703–711 (2017). ijcai.org

  8. Nadel, A., Ryvchin, V.: Chronological backtracking: solvers. goo.gl/ssukuu

  9. Neves, M., Martins, R., Janota, M., Lynce, I., Manquinho, V.: Exploiting resolution-based representations for MaxSAT solving. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 272–286. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24318-4_20

    CrossRef Google Scholar 

  10. Pipatsrisawat, K., Darwiche, A.: A lightweight component caching scheme for satisfiability solvers. In: Marques-Silva, J., Sakallah, K.A. (eds.) SAT 2007. LNCS, vol. 4501, pp. 294–299. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72788-0_28

    CrossRef Google Scholar 

  11. Prosser, P.: Hybrid algorithms for the constraint satisfaction problem. Comput. Intell. 9(3), 268–299 (1993)

    CrossRef Google Scholar 

  12. Marques Silva, J.P., Lynce, I., Malik, S.: Conflict-driven clause learning SAT solvers. In: Biere et al. 2, pp. 131–153

    Google Scholar 

  13. Marques Silva, J.P., Sakallah, K.A.: GRASP - a new search algorithm for satisfiability. In: ICCAD, pp. 220–227 (1996)

    Google Scholar 

  14. Shtrichman, O.: Tuning SAT checkers for bounded model checking. In: Emerson, E.A., Sistla, A.P. (eds.) CAV 2000. LNCS, vol. 1855, pp. 480–494. Springer, Heidelberg (2000). https://doi.org/10.1007/10722167_36

     
   

 

文献Trail Saving on Backtrack学习笔记

      该文从NCB结合saving-phase形成大量重复赋值的角度分析了回溯，提出了新的算法，尽管仍回溯到Lback，但可以使随后的重降更有效率。
 

    该文的出发点有两个：

 
   
 

References

  1. Audemard, G., Simon, L.: Predicting learnt clauses quality in modern SAT solvers. In: Boutilier, C. (ed.) IJCAI 2009, Proceedings of the 21st International Joint Conference on Artificial Intelligence, Pasadena, California, USA, 11–17 July 2009, pp. 399–404 (2009). http://ijcai.org/Proceedings/09/Papers/074.pdf

  2. Gent, I.P.: Optimal implementation of watched literals and more general techniques. J. Artif. Intell. Res. 48, 231–251 (2013). https://doi.org/10.1613/jair.4016

    CrossRef MathSciNet MATH Google Scholar 

  3. Heule, M., Järvisalo, M., Suda, M. (eds.): Proceedings of SAT Competition 2018: Solver and Benchmark Descriptions. University of Helsinki (2018). http://hdl.handle.net/10138/237063

  4. Heule, M., Järvisalo, M., Suda, M. (eds.): Proceedings of SAT Race 2019: Solver and Benchmark Descriptions. University of Helsinki (2019). http://hdl.handle.net/10138/306988

  5. Hickey, R., Bacchus, F.: Speeding up assumption-based SAT. In: Janota, M., Lynce, I. (eds.) SAT 2019. LNCS, vol. 11628, pp. 164–182. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-24258-9_11

    CrossRef MATH Google Scholar 

  6. Jiang, C., Zhang, T.: Partial backtracking in CDCL solvers. In: McMillan, K., Middeldorp, A., Voronkov, A. (eds.) LPAR 2013. LNCS, vol. 8312, pp. 490–502. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-45221-5_33

    CrossRef Google Scholar 

  7. Luo, M., Li, C., Xiao, F., Manyà, F., Lü, Z.: An effective learnt clause minimization approach for CDCL SAT solvers. In: Sierra, C. (ed.) Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI 2017, Melbourne, Australia, 19–25 August 2017, pp. 703–711. ijcai.org (2017). https://doi.org/10.24963/ijcai.2017/98

  8. Möhle, S., Biere, A.: Backing backtracking. In: Janota, M., Lynce, I. (eds.) SAT 2019. LNCS, vol. 11628, pp. 250–266. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-24258-9_18

    CrossRef Google Scholar 

  9. Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: engineering an efficient SAT solver. In: Proceedings of the 38th Design Automation Conference, DAC 2001, Las Vegas, NV, USA, 18–22 June 2001, pp. 530–535. ACM (2001). https://doi.org/10.1145/378239.379017

  10. Nadel, A.: Understanding and improving a modern SAT solver. Ph.D. thesis, Tel Aviv University (2009)

    Google Scholar 

  11. Nadel, A., Ryvchin, V.: Chronological backtracking. In: Beyersdorff, O., Wintersteiger, C.M. (eds.) SAT 2018. LNCS, vol. 10929, pp. 111–121. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94144-8_7

    CrossRef Google Scholar 

  12. Nieuwenhuis, R., Oliveras, A., Tinelli, C.: Solving SAT and SAT modulo theories: from an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL(T). J. ACM 53(6), 937–977 (2006). https://doi.org/10.1145/1217856.1217859

    CrossRef MathSciNet MATH Google Scholar 

  13. Silva, J.P.M., Lynce, I., Malik, S.: Conflict-driven clause learning SAT solvers. In: Handbook of Satisfiability, pp. 131–153. IOS Press (2009). https://doi.org/10.3233/978-1-58603-929-5-131

  14. van der Tak, P., Ramos, A., Heule, M.: Reusing the assignment trail in CDCL solvers. JSAT 7(4), 133–138 (2011). https://satassociation.org/jsat/index.php/jsat/article/view/89

    MathSciNet MATH Google Scholar 

  15. Xiao, F., Luo, M., Li, C.M., Manya, F., Lü, Z.: MapleLRB LCM, Maple LCM, Maple LCM dist, MapleLRB LCMoccRestart and glucose-3.0+ width in SAT competition 2017. In: Balyo, T., Heule, M.J.H., Järvisalo, M.J. (eds.) Proceedings of SAT Competition 2017: Solver and Benchmark Descrptions, pp. 22–23. University of Helsinki (2017). http://hdl.handle.net/10138/224324
   
posted on 2023-09-01 10:09  海阔凭鱼跃越  阅读(95)  评论(0)  编辑  收藏  举报