| 1.数字化工具的新特征 | |
|
。。。。 物理机-->虚拟化-->容器化 |
|
|
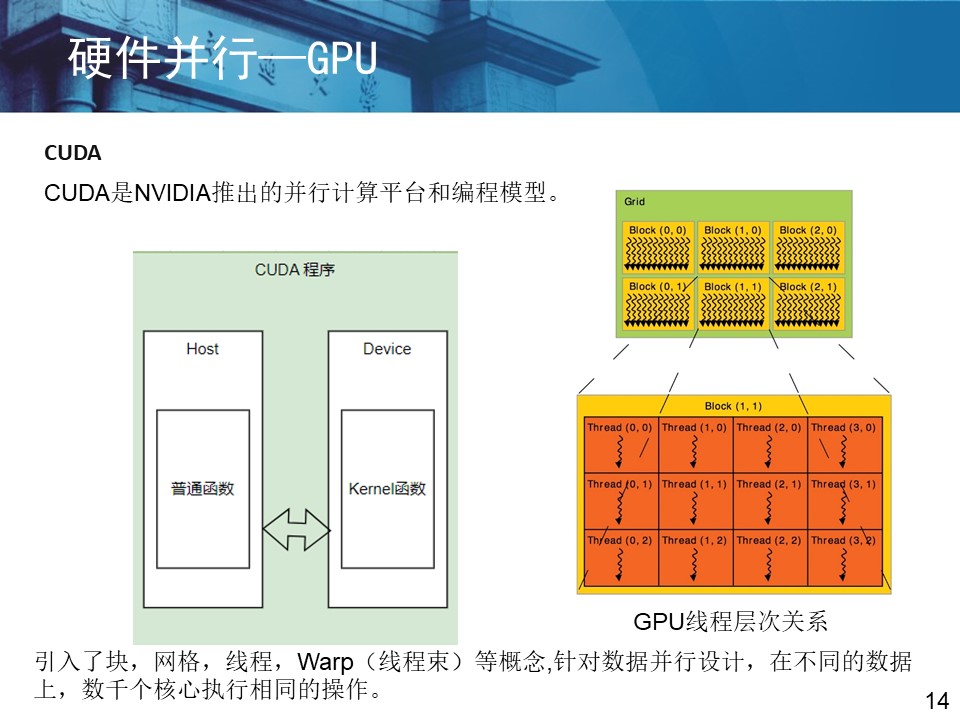
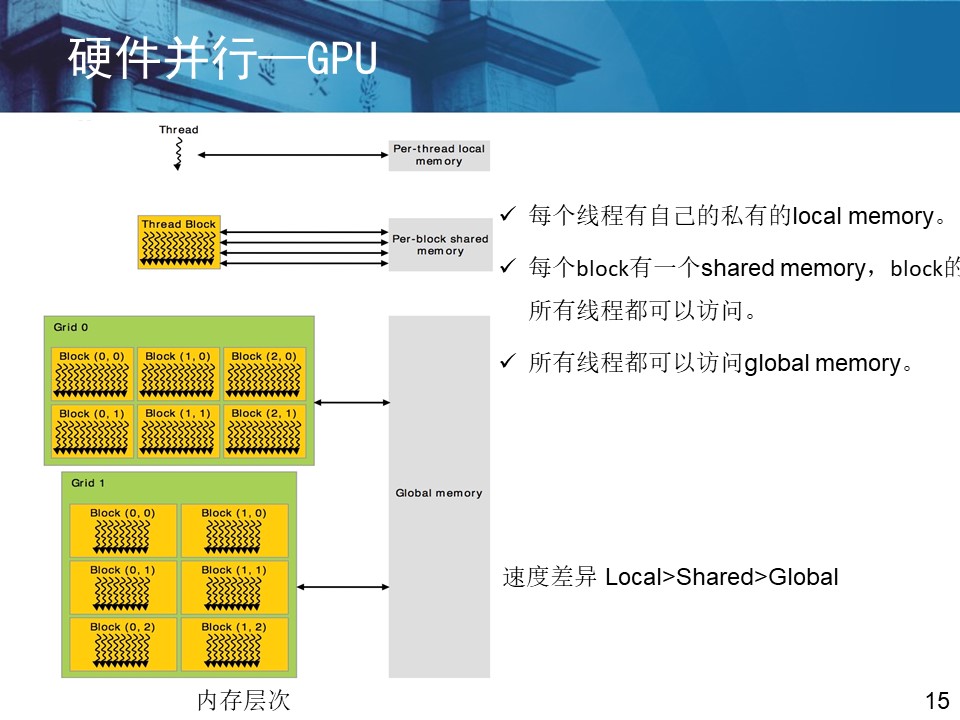
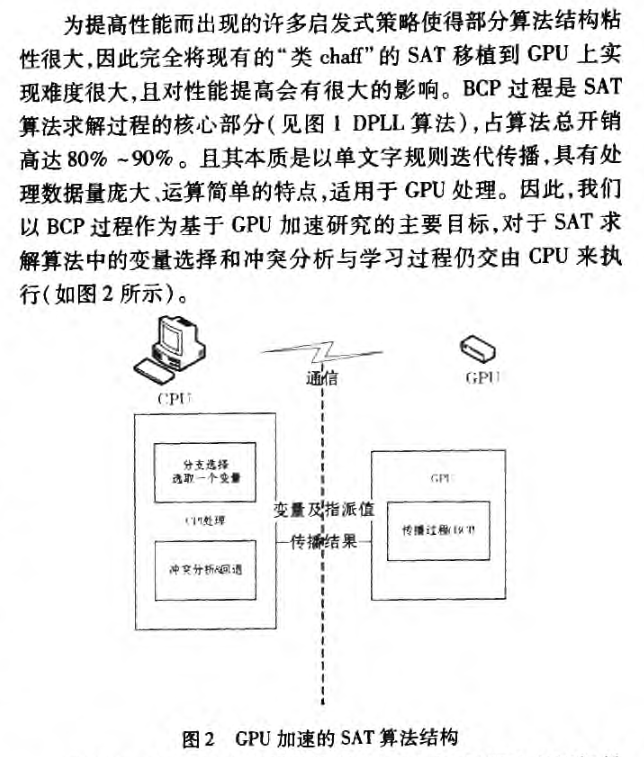
2.分布式并行编程基础 (1)传相关并行编程框架: MPI(消息传递接口)——一种典型的并行编程框架 OpenCL CUDA (2)HDFS分布式文件系统下的MapReduce并行模式 shuffle 调度 |
|
|
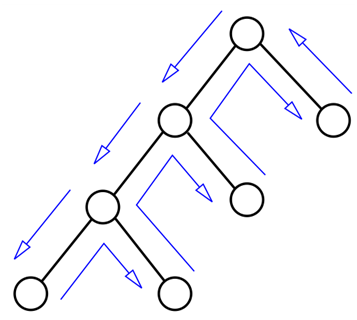
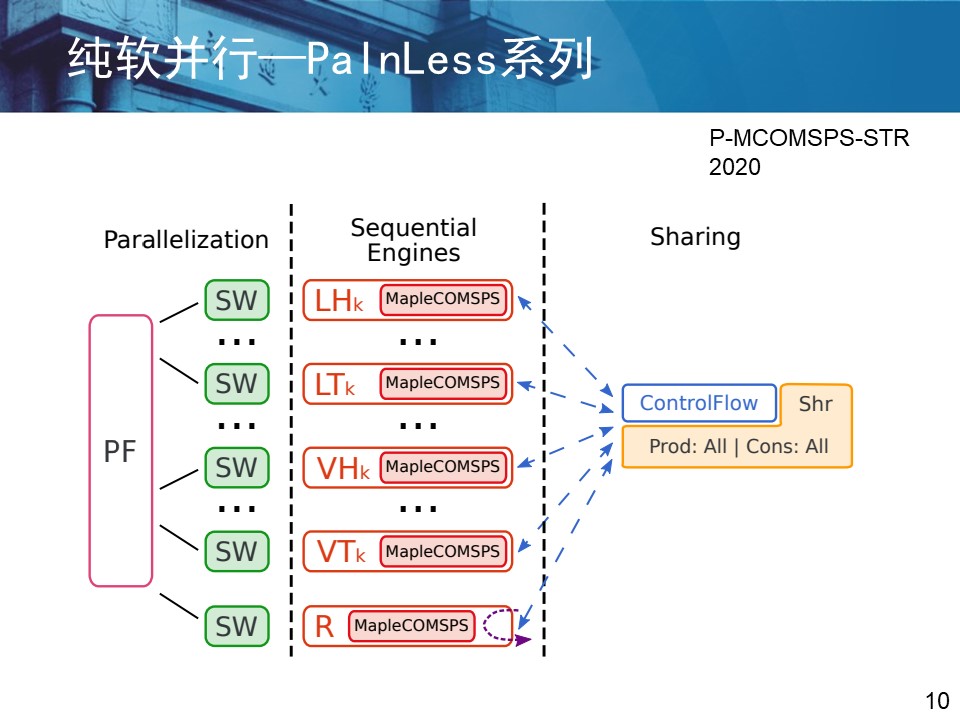
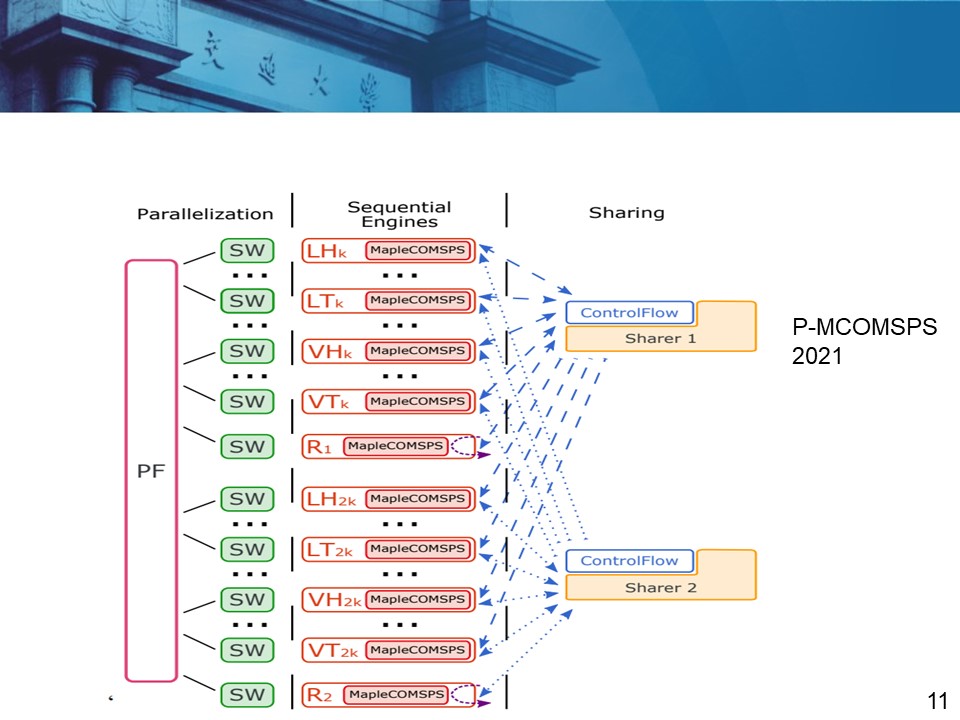
3.并行求解器研究现状 3.1 纯软并行相关概念 DPLL算法 —— 求解空间树深度优先搜索 DPLL本质上是在二叉搜索树上进行回溯,如图所示是不带回跳的常规搜索。
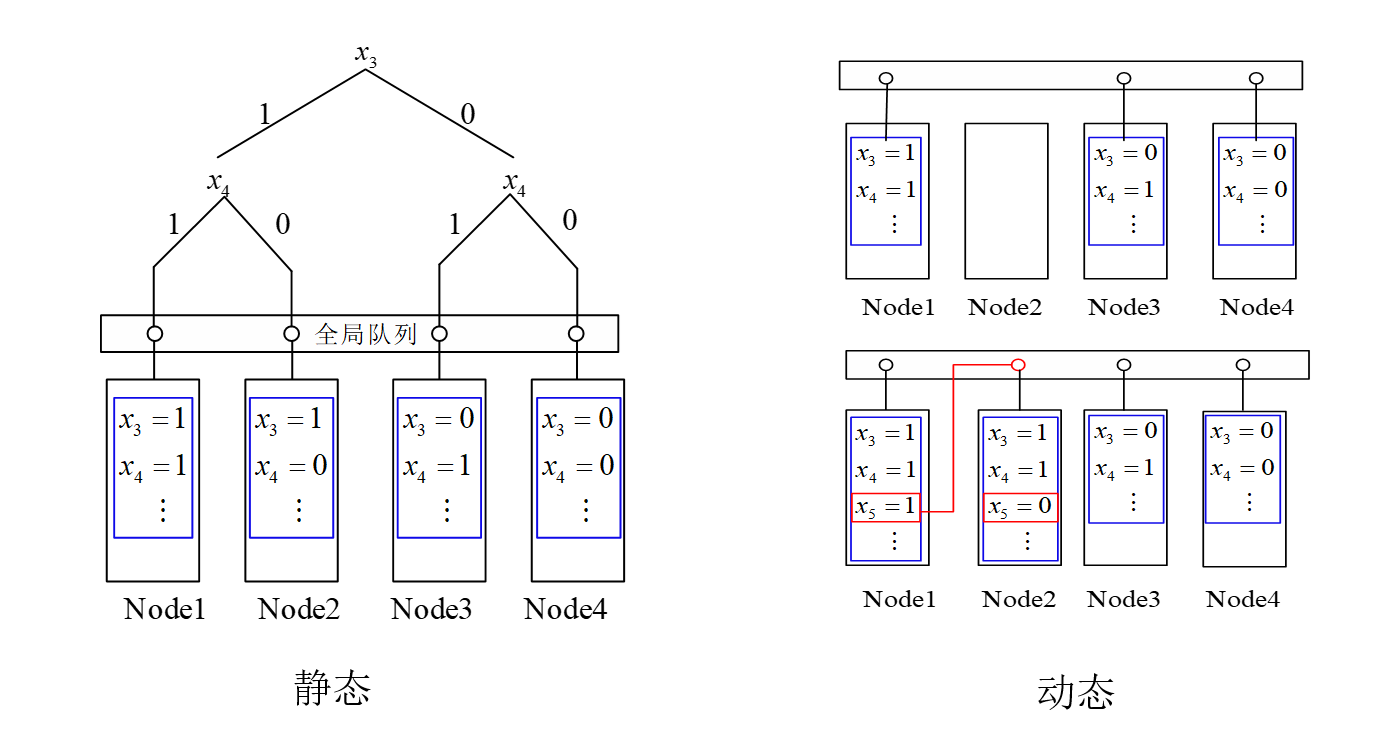
从任务划分形式上分为分治并行、组合并行和混合并行。 (1)分治并行
(2)组合并行 这类方式主要是在不同的计算节点上并行不同的搜索算法,或者并行同一个搜索算法配置不同的参数。各个节点相互独立的运行,其中任何一个节点求解出公式集的可满足例或证明其不可满足时,其余节点终止计算。 ManySAT、ppfolio、Syrup以及PLingeLing,等均采用了组合并行的方式。
(3)混合并行 混合并行是指将前两种并行方式结合起来使用,利用搜索树划分的方式缩减子句集的规模,然后再对子问题进行组合并行求解。 PaInLess框架就属于混合并行,即提供了分治策略也提供了组合策略。
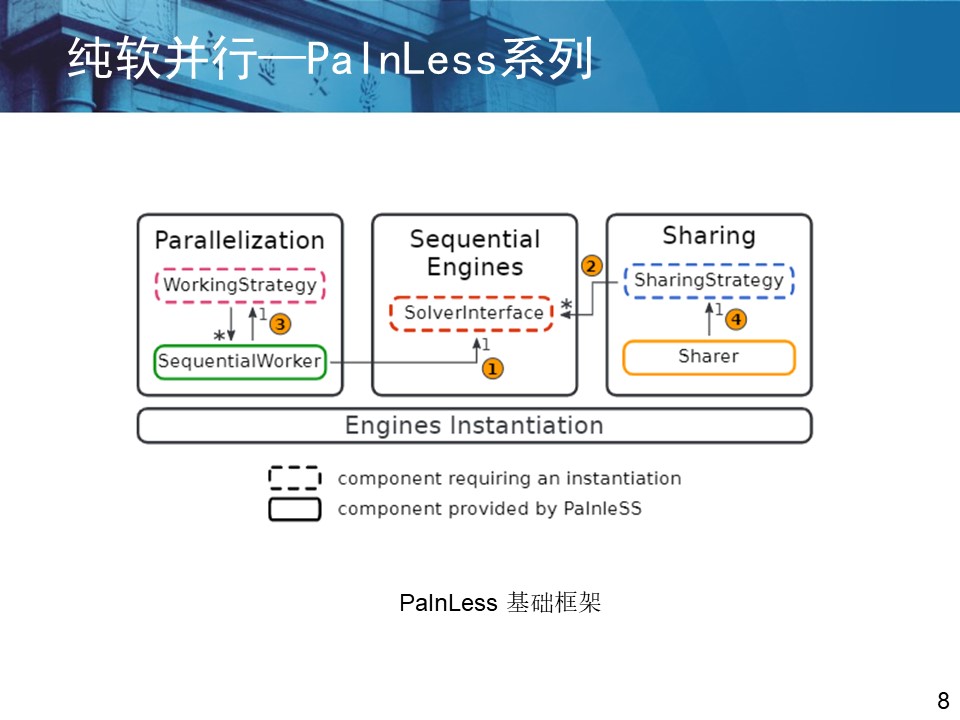
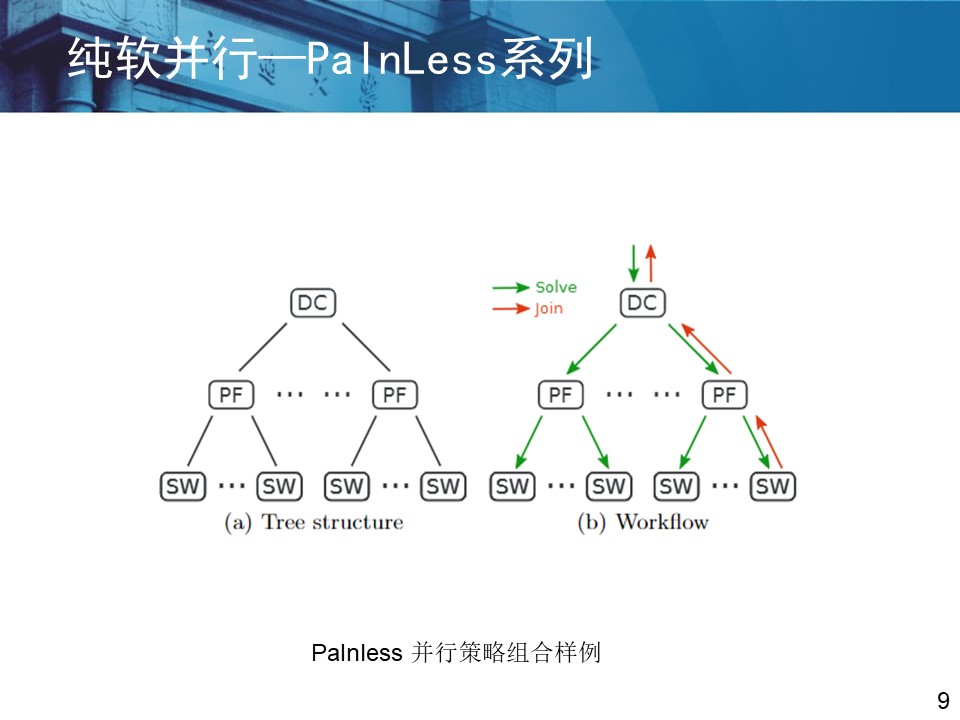
3.2 研究的时间线与几个主要的几个框架 (摘自西南交通大学吴贯锋老师2023年相关学术交流PPT)
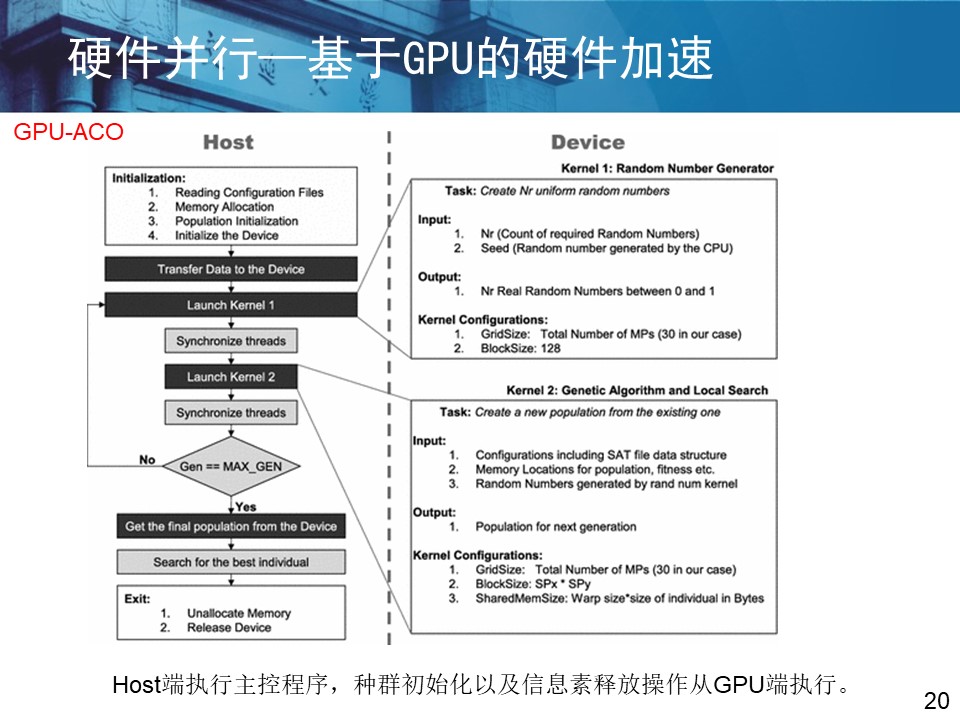
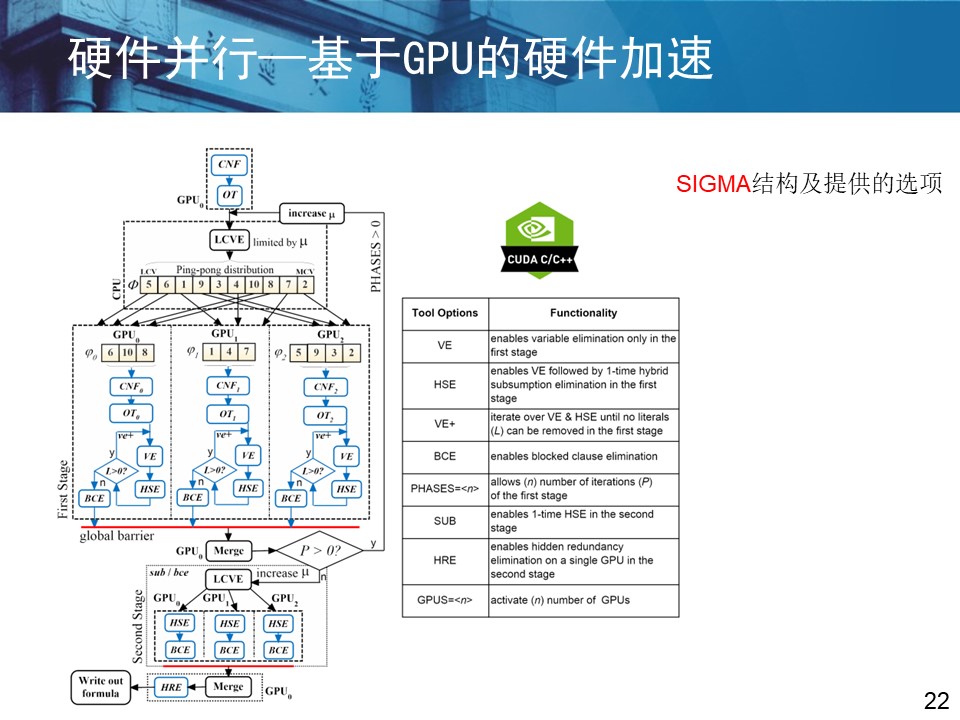
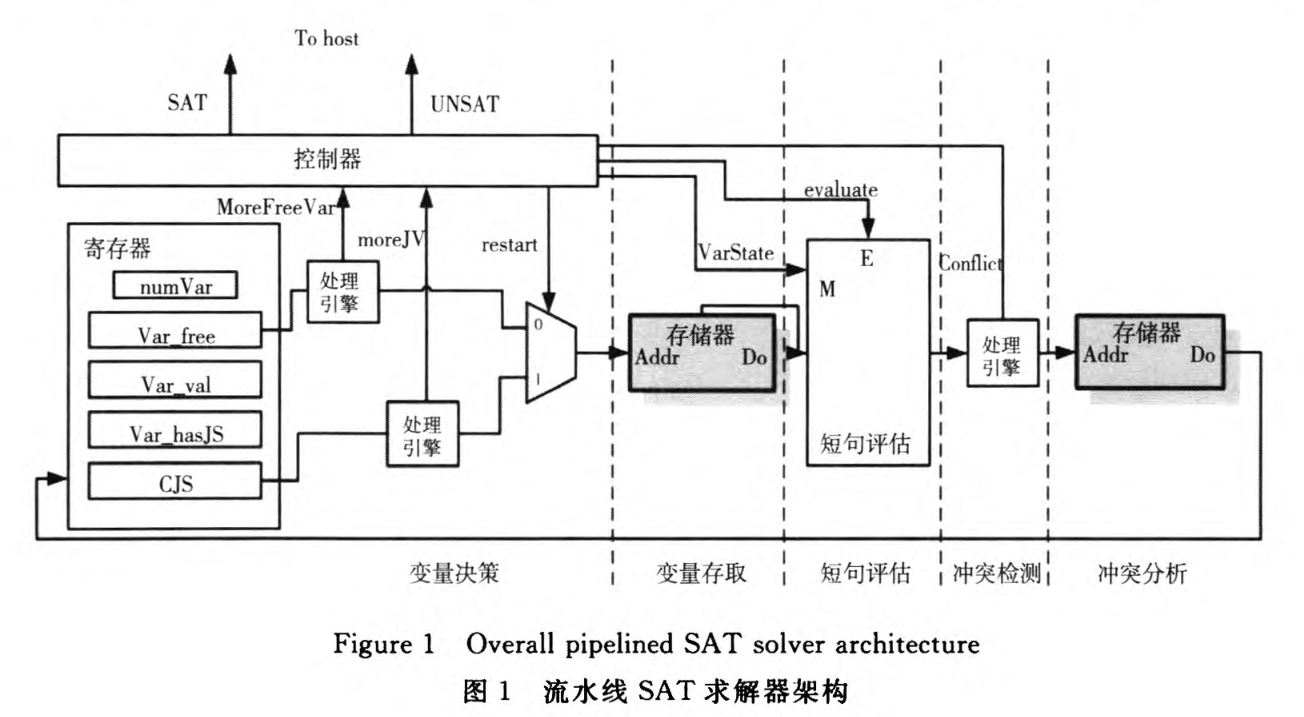
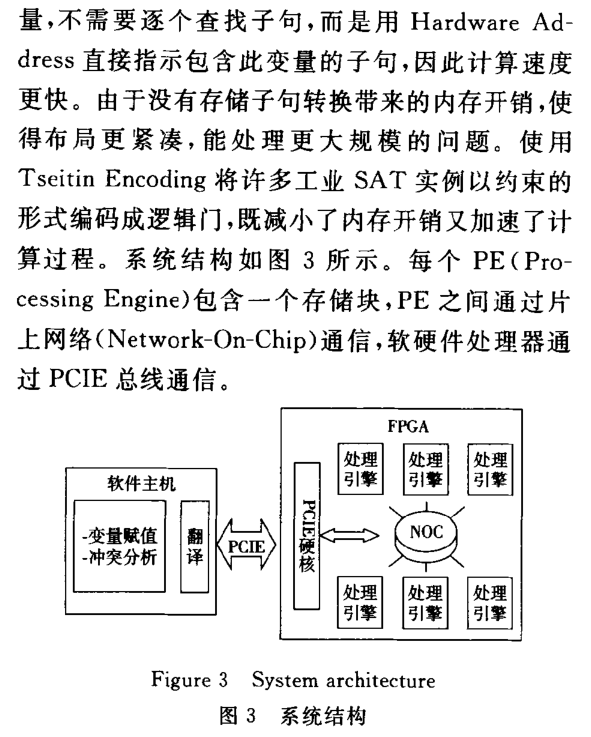
3.3 有关求解器硬件加速的研究
4 相关论文学习 4.1 国防大学王鹤老师2011发表论文摘录 王鹤.面向GPU的可满足性求解技术研究[D].国防科学技术大学[2023-08-27].DOI:10.7666/d.d138875. 面向GPU的可满足性求解技术研究
(补充本截图最后一句)发加速的研究,因而算法性能的提高并不理想。
|
|
|
4.2 西南交通大学吴贯锋老师2019发表论文摘录 吴贯锋,徐扬,常文静,等.基于OpenMP的并行遗传算法求解SAT问题[J].西南交通大学学报, 2019, 54(2):8.DOI:10.3969/j.issn.0258-2724.20170700.
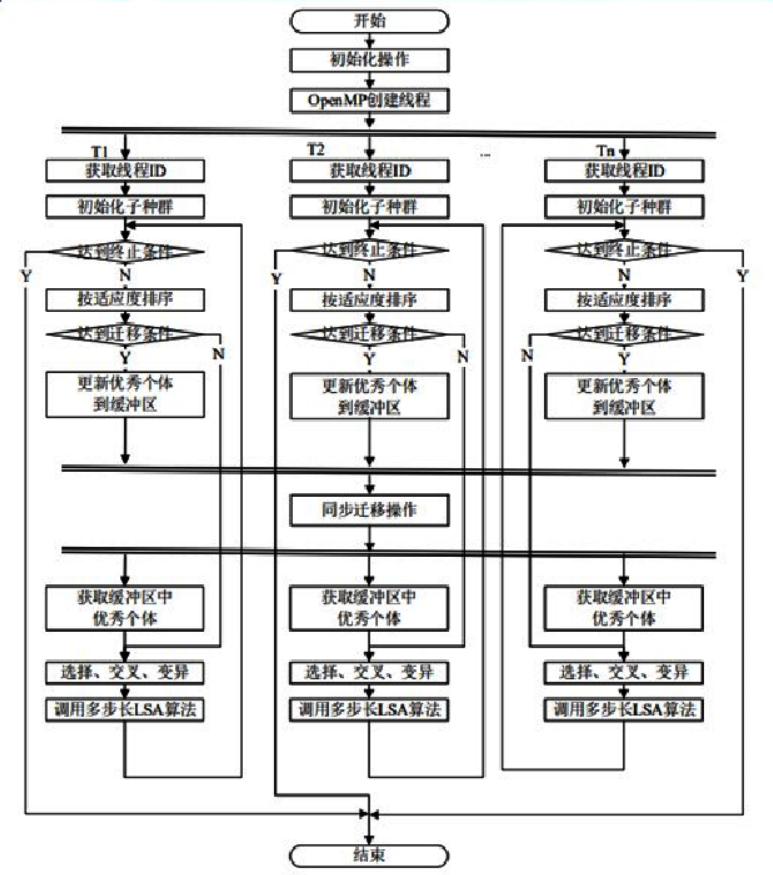
该文献运用遗传算法随机求解器在多线程中的组合并行。 基于 OpenMP 的并行遗传算法求解 SAT 问题,本质上属于组合并行,并行节点中的任何一个种群中的任何一个个体进化到最优状态(个体取值使得所有子句可满足),算法即达到终止条件。不涉及解的分解和合并,个体的解,即是全局的解。
|
|
|
4.3 基于硬件可编程逻辑的SAT求解算法研究与进展 [1]马柯帆,肖立权,张建民,等.基于硬件可编程逻辑的SAT求解算法研究与进展[J].计算机工程与科学, 2016, 38(4):6.DOI:10.3969/j.issn.1007-130X.2016.04.003.
|
|
|
4.4 西南交通大学吴贯锋老师博士论文中关于并行部分
1. 并行编程框架 OpenMP
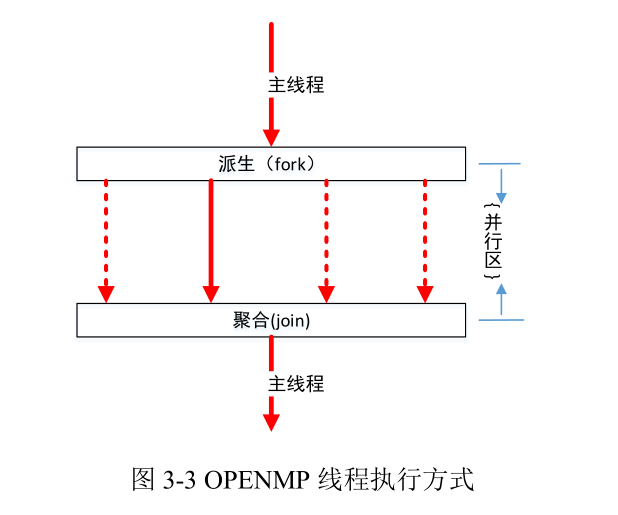
OpenMP 是一套编译预处理方案,包括一些编译制导指令和库函数。主要为共享内存计算机创建并行程序提供便利。采用派生和聚合的编程模型实现线程级别并行。 基于 OpenMP 编程模型的程序启动时只有一个主线程执行任务,在需要并行执行的时候由编译制导语句控制派生出新的线程,这些新的线程构成了线程组。并行区中的代码被分配到线程组中的线程并行运行。在并行区结尾处,如果设置有同步操作,则主线程等待所有线程聚合,聚合后主线程继续执行或结束返回,否则,主线程和线程组中的其他线程异步执行,主线程到达并行区结尾时,并不等待其他线程完成聚合操作[216]。派生和聚合如图 3-3 所示。
OpenMP 编程模型降低了并行程序开发的门槛,研究或开发人员不必完全掌握线程并行内部实现细节,仅通过编译制导语句就能实现线程级别并行。将更多精力围绕研究问题本身,提高了研发效率。
数据共享 在 OpenMP 并行区域中,并行区域外的变量都是共享变量,也可以用#pragma omp parallel shared 实现数据的共享操作。无论何种共享方式,多个子群分布在不同的线程上并行进化,对于全局共享数据的读写操作都会发生数据竞争。读写线程发生数据竞争,会导致读取脏数据,写入不完整数据等漏洞发生,导致程序运行不可控。在多线程环境下必须注意数据竞争问题。 基于 OpenMP 的混合并行遗传算法设置全局二维向量ShareBuffer 作为各个线程执行迁移操作的最优个体资源池。二维向量的第一维度为线程 ID,第二维为该线程对外共享的优秀个体集合。并行区内的线程只操作自己对应的缓冲区,不存在数据竞争操作。 在所有线程进化到设定代数时,在并行区内部通过#pragma omp barrier 编译制导语句等待所有线程完成将优秀个体存入共享资源池操作。通过#pragma omp single 选择任意一个线程按迁移策略执行所有线程的优秀个体的迁移操作。
负载均衡问题 OpenMP 应用程序在存在多个同步操作语句时,采用#pragma omp barrier 设置同步操作,在其中一个线程最先达到同步点时,等待其他线程到达同步点。若线程任务分配不均衡,则整个并行效率取决于执行最慢的线程的执行效率,其他线程处于零负载等待状态,并没有充分利用计算机性能以及发挥出并行程序效率。 在基于 OpenMP 的并行混合遗传算法中,各线程对相同规模的个体执行相同的迭代次数,以及相同的遗传操作,因此理论上在并行区内各线程的负载程度完全一致,仅在迁移操作时随机选择一个线程对共享资源池中的个体进行迁移,其他线程处于等待状态,因此程序中不存在负载失衡的情况。
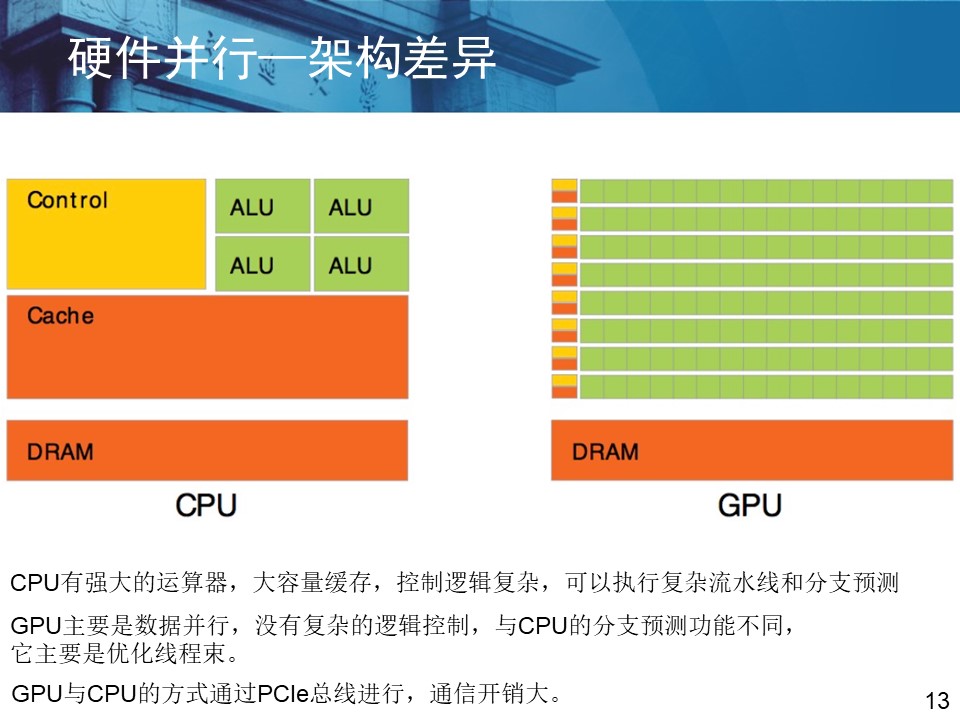
2.硬件加速与纯硬件设计求解器的差异 纯软的 SAT 求解器中采用的算法和策略在硬件加速的 SAT 求解器中并不适用。
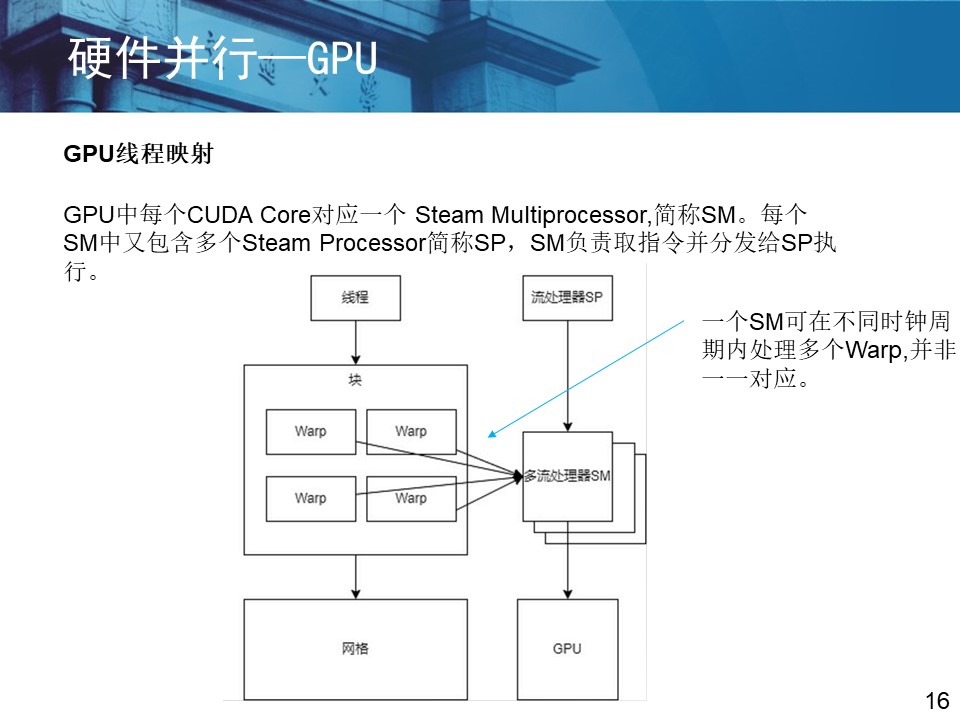
3. cpu与GPU协同计算 GPU 与 CPU 架构不同,GPU 采用的是单指令多线程 (Single Instruction Multiple Thread,SIMT)的并行处理模式,一个 GPU 中包含成百上千被称为核的处理单元。若干个核被集成在一起称之为流多处理器 (Stream Multiprocessors,SM)。 在 CPU 与 GPU 协同计算中,CPU 端被称为宿主 Host 端,GPU 端被称为设备Device 端。在 GPU 上执行的函数被称为核 kernel 函数。 3.1 SAT 问题并行求解框架 在基于硬件加速的 SAT 问题求解方面,硬件提供了多线程的并发机制,因此分治是最适合硬件并行加速求解 SAT 问题的并行方式。 (1)并行 DPLL 算法 分治并行是在 DPLL 算法的基础上,预先对二叉树中的变量节点赋值,并行搜索不同的子空间,分而治之,算法 4-1 是基于分治的并行 DPLL 算法描述。
(2)分治算法 3-SAT-DC 针对 3-SAT 问题,文献[244]中提出了另外的一种分治算法 3-SAT-DC,算法依据 3-SAT 问题特点递归的判定各分支的赋值情况,Fujii 在文献[235]中在此算法框架内做 GPU加速 BCP 过程。
(3)并行布尔约束传播算法 BCP 算法过程本质上是重复执行单文字子句规则的过程,由 BCP 过程产生的文字赋值与决策文字处在同一决策层上,传播文字赋值的先后顺序不影响推导结果(注:非冲突层传播文字赋值顺序不影响推导结果)。因此,赋值文字的再推导传播过程可并行执行。
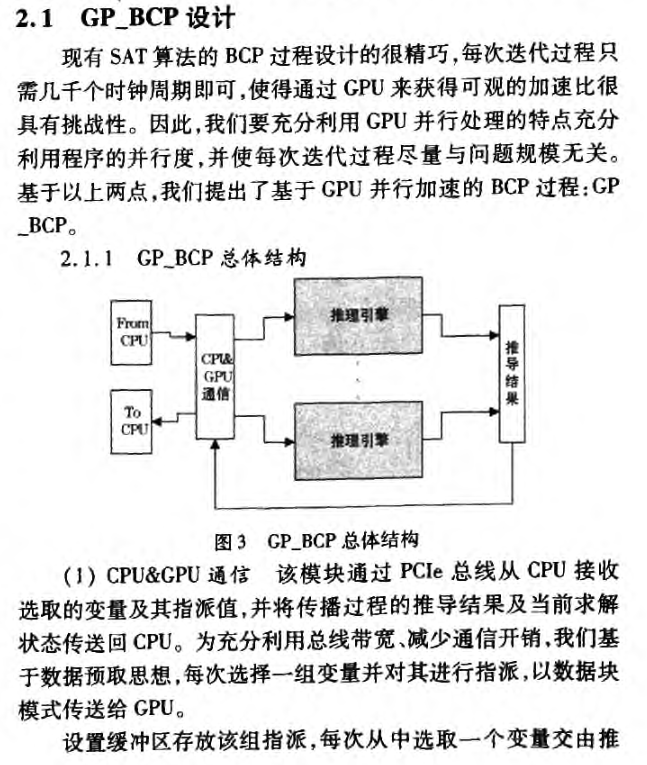
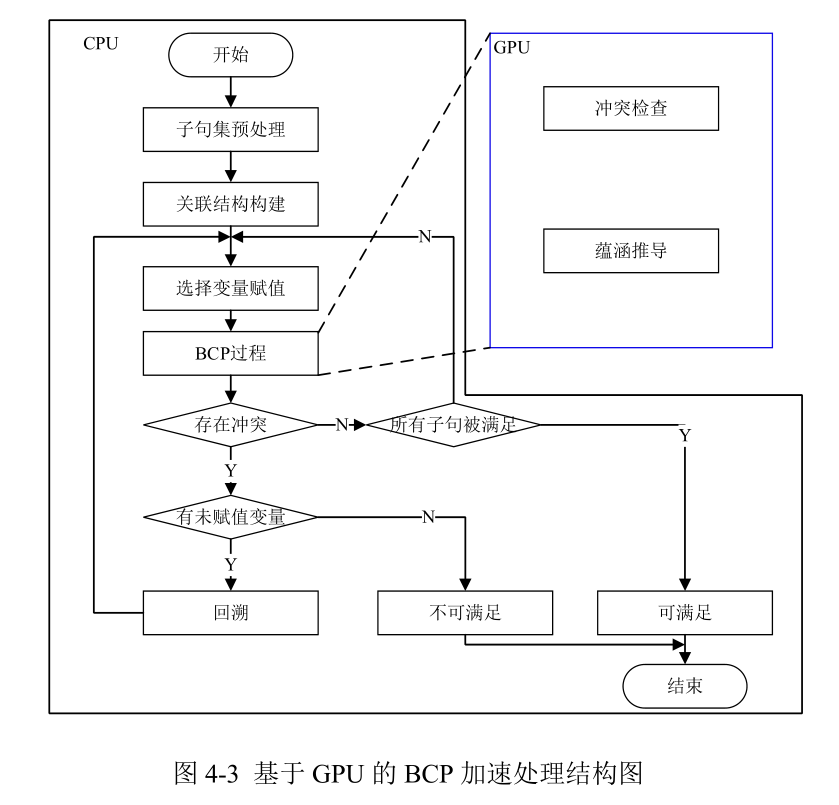
4. 基于 GPU 的 BCP 加速
4.1 整体流程
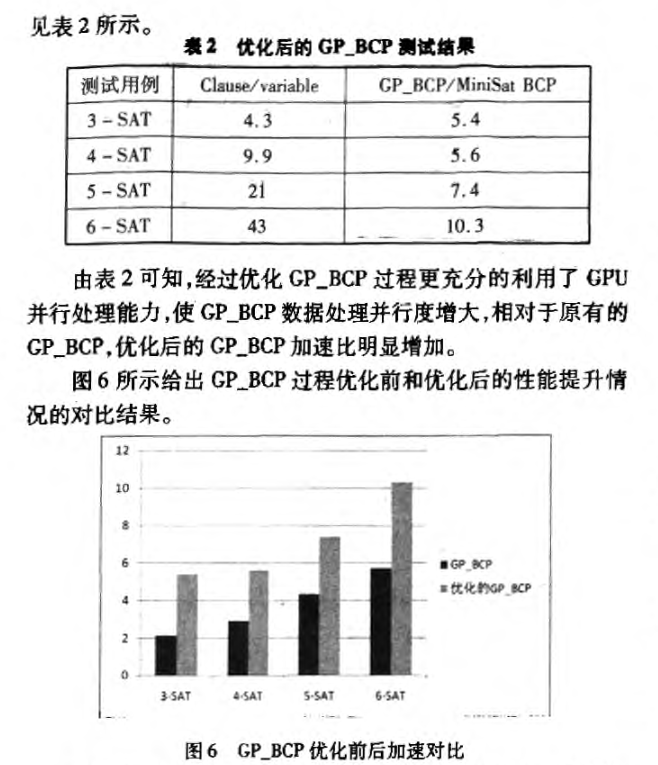
虽然已有采用 GPU 对 SAT 问题求解中的 BCP 算法加速的研究,但是其并未充分发挥 GPU 应有的性能,算法和程序结构上有很大的改进。 第一,采用子句分组并行 BCP的方式并行效率直接受子句集规模的影响; 第二,纯粹的分治算法本质上属于暴力破解算法,针对小的问题有效,但是,若问题规模变大,GPU 硬件资源有限并行效率十 纯软的 SAT 求解器经过几十年的发展,模块相对成熟,且许多算法设计相当精致高效,如重启、冲突子句学习、启发式文字选择策略等。硬件并行加速与纯软的SAT 求解器对比达到相当的效果很难。
4.2 数据结构设计
GPU 中线程块中线程调度以线程束为基本单位,数据存取一次存取 16 字节的整数倍数据时比单个存取效率要高。数据存储未对齐时会导致额外的内存访问,降低线程执行效率。因此,子句存储应考虑到数据的对齐方式。
图 4-4 中每个方框代表 4 个字节的长度,在 3-SAT 问题的子句只有三个文字,附带一些标志位信息,可采用 4 个整型表示,且在 GPU 中内置类型 int4 恰好为一次存储访问的大小。 读取子句集时构建文字子句关联列表。监测文字列表中每个整型表示一个变元,整型中取两个 bit 位表示变元赋值情况,一个 bit 表示该变元是否是监测文字。剩余 29 个 bit 位表示关联列表起始标号,理论上可存储子句 2^29-1 个。 在关联子句列表中地址下标的第一个粗体数字表示变元关联的子句个数 M,后跟M 个整型数表示对应的子句标号。与此同时,为了适应 GPU 存储,数据以 4 个整型的方式补齐,如图中标号 03、09、10 与 11 均是为了对齐而填充的空数据。
4.3 GPU-BCP 算法描述
expr 表示原始子句集, d_sp_trail 表示赋值顺序栈, d_var_to_cla 表示所有变元关联的子句列表,对应于图 4-4 中的“文字子句关联列表”。 d_var_index 表示变元对应的关联子句列表的起始位置对应于图 4-4 中“检测文字列表”。 d_conf_inf 为长度为 4 的整型数组, d_conf_inf[0]为冲突标识,为 1 时表示本次内核调用存在赋值冲突; d_con_inf[1]为蕴涵标识,为 1 时表示本次内核执行有新的变量被赋值; d_conf_inf[2]记录了当前正在传播的文字在 d_sp_trail 中的下标。 d_conf_inf[3]记录了赋值栈d_sp_trail 的长度; 需要注意的是 BCP 函数中的参数均存储在设备端,发生冲突时设备端的内容不向主机端拷贝,减少了 GPU 与 CPU 之间数据传递的开销。
在 GPU 中,线程调度以线程束为单位,同一时刻,一个线程束内的线程执行相同的指令。GPU 线程束的分化问题是指 GPU 中的逻辑运算单元不具有对分支指令的预测功能,若在 GPU 的线程束内部存在一个分支语句,则线程束内部有一半的线程因条
4.4 实验分析
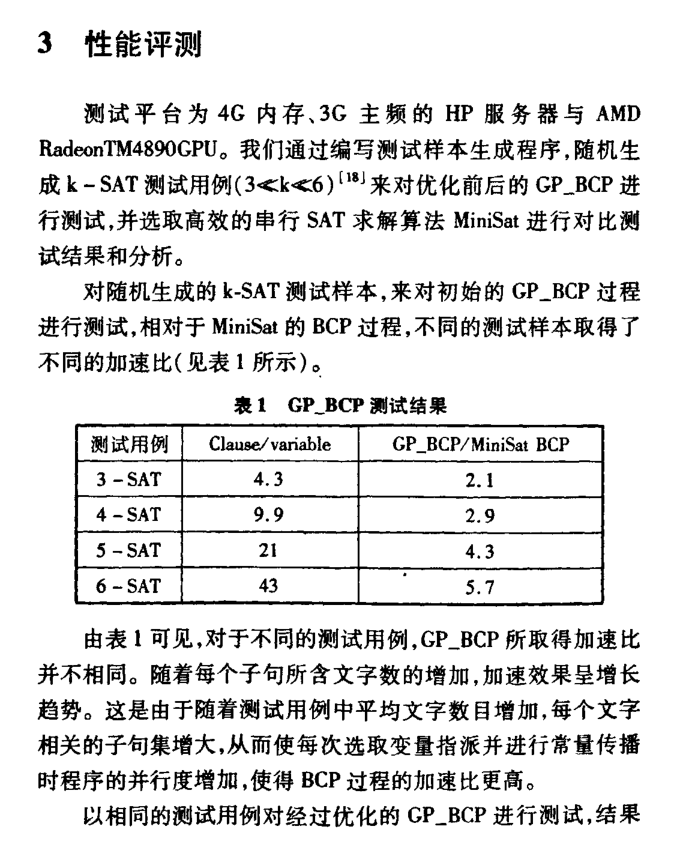
在子句规模较小时,针对单个问题的并行加速性能体现不明显。为了验证线程分化对 GPU 求解效率的影响,以文字数 150 子句数 645 的 100 个 cnf 文件作为测试例,以所有问题的总求解时间作为衡量指标。则优化前和优化后 100 个问题的总求解时间相
通过实验对比发现,本章节提出的采用在 GPU 上采用文字子句关联结构实现 BCP算法在一定程度上提高了利用 GPU 求解 3-SAT 问题的效率,但是由于求解机制的不同与纯软的 SAT 求解器对比如 Glucose、LingeLing 等对比,仍有差距。
本章节旨在研究采用 GPU 进行 BCP 过程加速的改进算法,通过对采用 CPU 加速3-SAT 问题求解中的 BCP 算法进行改进,取得了预期的改进效果。然而 GPU 并行加速本质上属于利用硬件的并行性分治求解问题,受限于求解机制的不同,在并行核心数不多的情况下与纯软的 SAT 求解器相比仍有一些差距。后续研究可考虑在 GPU 上实现冲突子句学习的算法,以期充分发挥 GPU 性能。或在条件允许的情况下,加大 GPU硬件数目,以 GPU 网格的方式并行能够在较短时间求解出规模较大的问题。
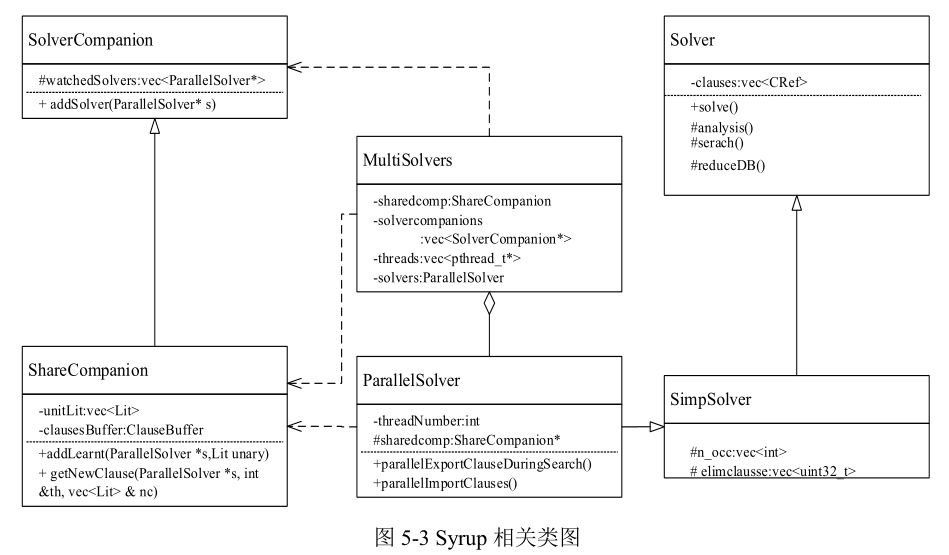
5. 并行求解器中改进的子句共享策略 5.1 并行节点间子句分享策略 (1)共享的数据结构
(2)学习子句的导出与导入 Syrup 在处理并行节点间的子句分享时比较慎重,其认为 LBD 值小于 8,子句长度小于 40 的子句是“好的”子句应该被分享,其次,为了避免节点之间在求解的初期相互干扰,在每个节点的冲突次数未达到 5000 次的情况下,禁止分享学习子句。 其执行懒散的子句分享策略,在子句被分享前,先观察其被应用于冲突分析的次数,只有在冲突分析中出现过的子句才可以被共享。与串行版本中策略一致,限制分享的子句 LBD 值小于等于 8,子句长度小于 40,单元子句则直接被分享。 Syrup 在搜索过程中如果冲突次数已经达到 5000 次,则可执行外部学习子句的导入操作。首先导入一元子句,然后导入其它满足评估条件的学习子句。
5.2 混合评估方式下的子句分享策略 在并行节点的 search 函数执行过程中,当赋值发生冲突时,analyze 函数分析冲突产生原因并获得学习子句。如果学习子句是单元子句则直接分享到共享内存队列,根据子句共享策略判断是否共享当前学习子句。 算法 5-3 为混合评估方式下的子句分享策略,以子句被使用次数限制作为条件代替原有的部分 LBD 限制条件。
实验中学习子句使用次数限制条件 LimitNum,需根据实验获取经验值设置。当前线程将优质学习子句导出到共享内存队列中,当其他线程中的 CDCL 算法执行重启操作时从共享队列中获取学习子句。
5.3 实验与分析 Glucose 是国际知名的 CDCL 求解器,其作者最主要的贡献是提出 LBD 评估算法并成功应用在求解器上,在 SAT 国际竞赛中多次获奖。2016 年 SAT 竞赛在 MainTrack组外还专门设置了最佳 Glucose 改进组奖项。 本文以 2017 年并行组冠军 Syrup(Glucose4.1 的并行版本)为基础版本,采用混合子句评估方法分别对 reduceDB()函数以及并行节点间子句共享策略部分的进行改进。 测试机软硬件环境如表 5-1 所示。
实验以 2017 年 SAT 竞赛 MainTrack 组 350 个基准例作为测试例,限时 3600 秒,所有测试机保证软硬件环境一致。根据前期实验分析结果显示,LimitNum 取值 150 时效果最好,即在规定时间内求解问题总数最多。并行版本中采用相同数值,每个测试例运行 5 次,取平均值作为统计结果。 实验中,我们采用 Syrup 在 SAT 竞赛中相同的配置,默认运行 24 个线程并行求解。为了分析混合子句评估与子句分享策略对求解结果的影响,设置了不同的组合方式形成不同的并行求解器。 参与对比分析的并行求解器均以 Syrup 为前缀命名,详细说明见表 5-2。
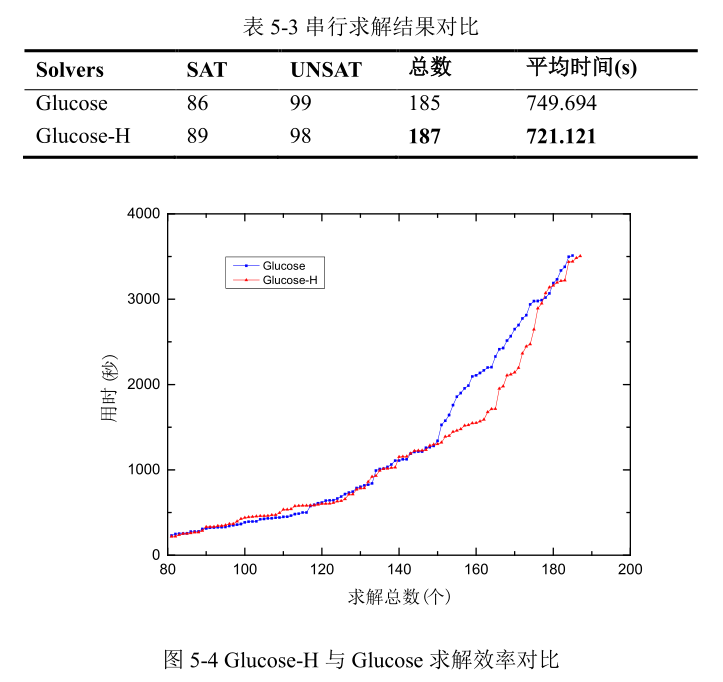
在 Glucose-H 中改变 LimitNum 大小,从 10 至 250 依次递增 10。我们发现求解个数在 LimitNum 取值为 150 时,改进效果最优。因此,后续实验 LimitNum 取值固定为150。首先,运行 Glucose 与基于混合评估策略的 Glucose-H。表 5-3 为运行结果。在求解个数上采用混合评估策略的Glucose-H 比Glucose求解问题在可满足实例上多3个,不可满足实例上少 1 个,整体多 2 个,求解平均时间比 Glucose 少 28.5 秒。
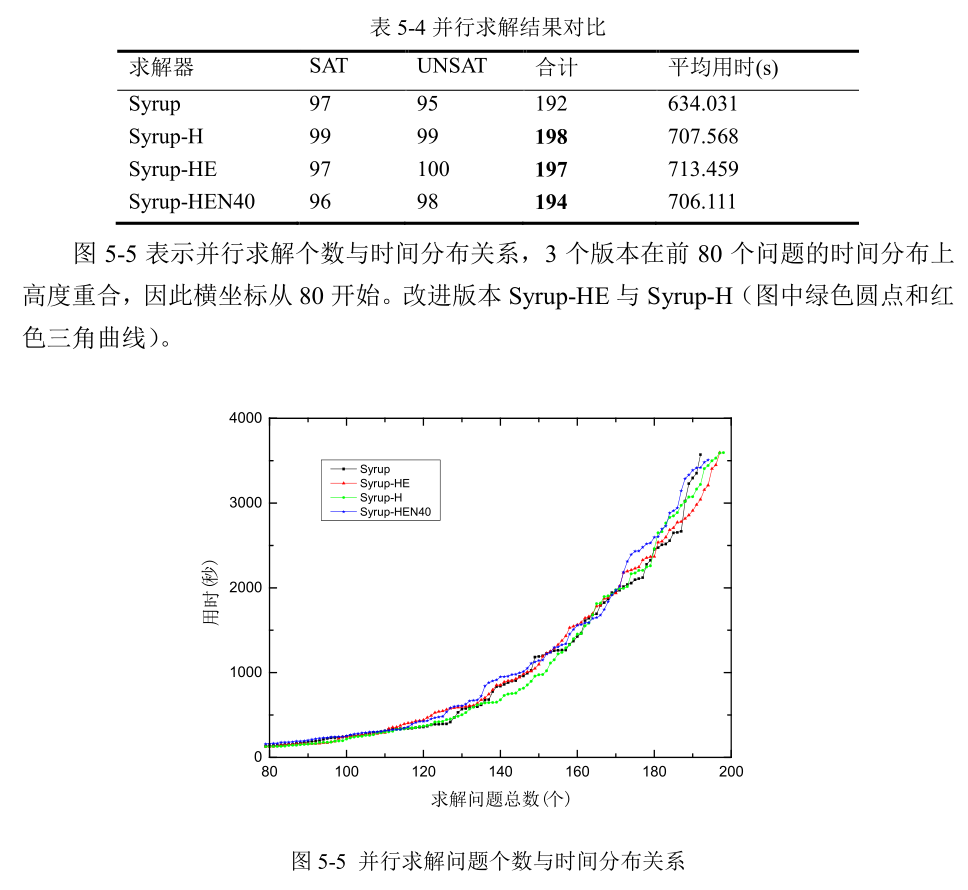
图 5-4 表示求解问题个数和所对应的时间的分布关系。图中所示,前 80 个问题曲线高度重合,因此为了更加清晰的展示差异,曲线横坐标从 80 开始。 从图中所示的曲线形态上分析,代表基于混合评估策略的 Glucose-H 的红色曲线明显低于代表 Glucose 的蓝色曲线,表明 Glucose-H 求解问题所用时间比 Glucose 要少,特别是对应于较难问题的[150,180]区间。
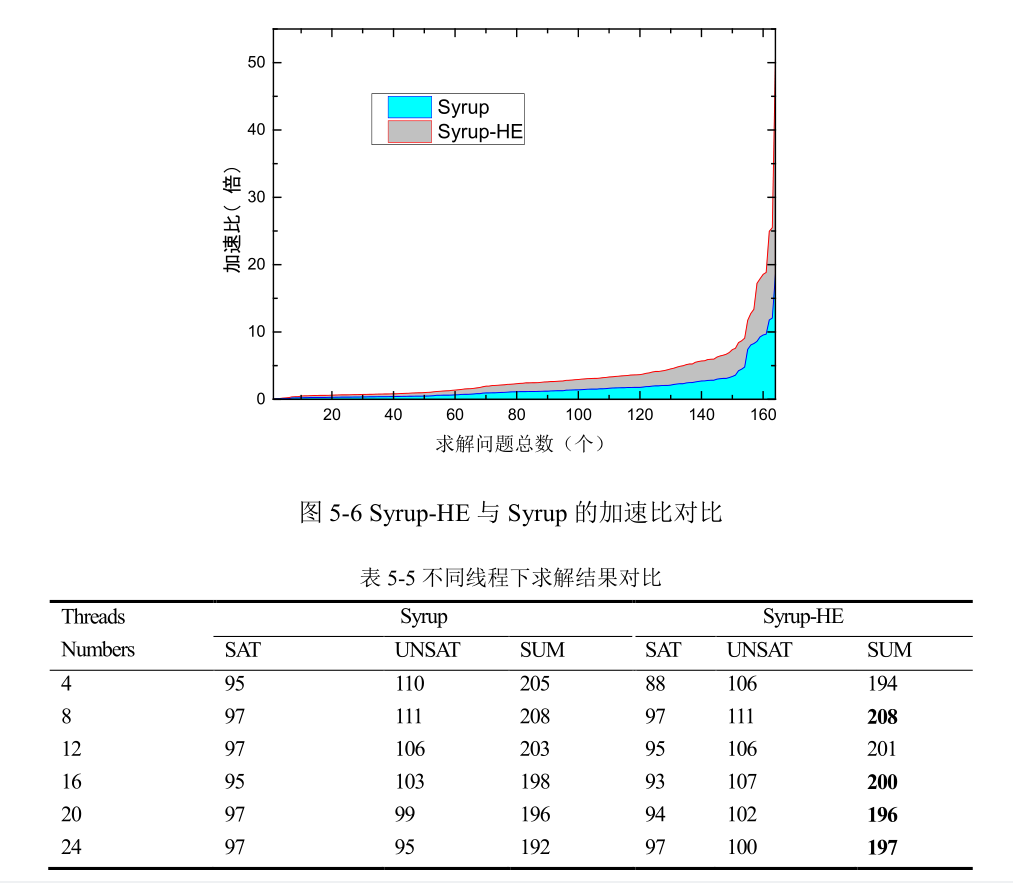
从曲线上看大部分区间低于代表原始版本 Syrup 的黑色线条,特别是在最后几个较难问题的求解上,代表 Syrup-HE 的红色三角线明显低于其余线条,表示所用时间比其他几个求解器要少。虽然求解问题总个数增加了 5 个,但是集中在较难的问题上,每个问题用时接近 3600 秒,因此拉高了所有问题的平均求解时间,这也是表 5-4 中改进版本平均用时比原版高的原因。 取 Syrup 与 Syrup-HE 做进一步分析,Glucose、Syrup 与 Syrup-HE 求解问题交叉部分个数为 166 个。剔除两条时间差异比较大(加速比大于 100)的噪声数据后,Syrup的平均加速比为 1.77863,Syrup-HE 的平均加速比为 1.89448。在相同线程数目下,求解相同的问题,Syrup-HE 所获得的加速比要比原版程序 Syrup 高。因此,采用混合评估方式的改进版本不仅增加了求解问题的个数,同时也提高了求解速度。加速比如图5-6 所示。 考虑到机器性能的影响,改变并行线程数,则 Syrup 与 Syrup-HE 的执行结果如表5-5 所示。两个求解器均在线程数为 8 的时候达到求解个数的峰值,随后求解个数开始随着线程个数增加回落,基于混合评估算法的求解器回落趋势较基于 LBD 评估方式的Syrup 有所减慢,求解个数比 Syrup 多,表中的粗体显示部分。 与此同时,虽然在线程数为 8 时 Syrup 与 Syrup-HE 求解问题个数完全相同,但是求解的问题并不一致相同。Syrup-HE 求解的问题中有 7 个 Syrup 并未求解出来。
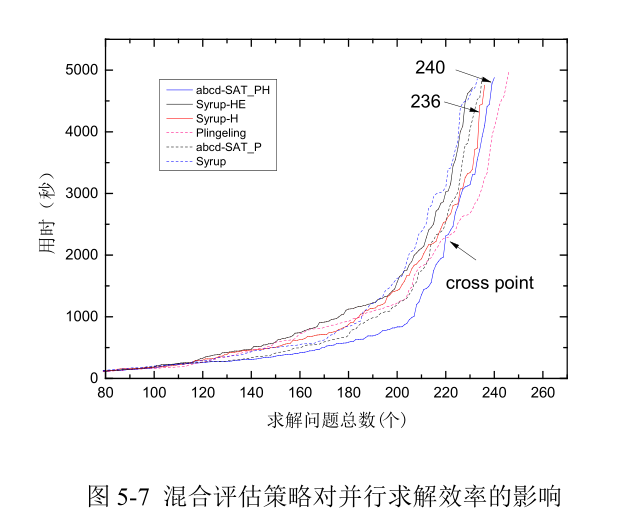
为了进一步评估混合学习子句评估算法的有效性,在选择与 Sryup 架构接近的abcd-SAT_P 作为新的基准版本,加入混合子句评估算法后形成版本 abcd-SAT_PH。限时 5000 秒,固定线程个数为 8,将 Syrup 改进系列、abcd-SAT 改进版本与 PLingeLing做对比(PLingeLing 在 2018 年竞赛并行组中,排名第二,求解个数与第一名一样,仅在时间上有细微差异),则对比情况如图 5-7 所示。
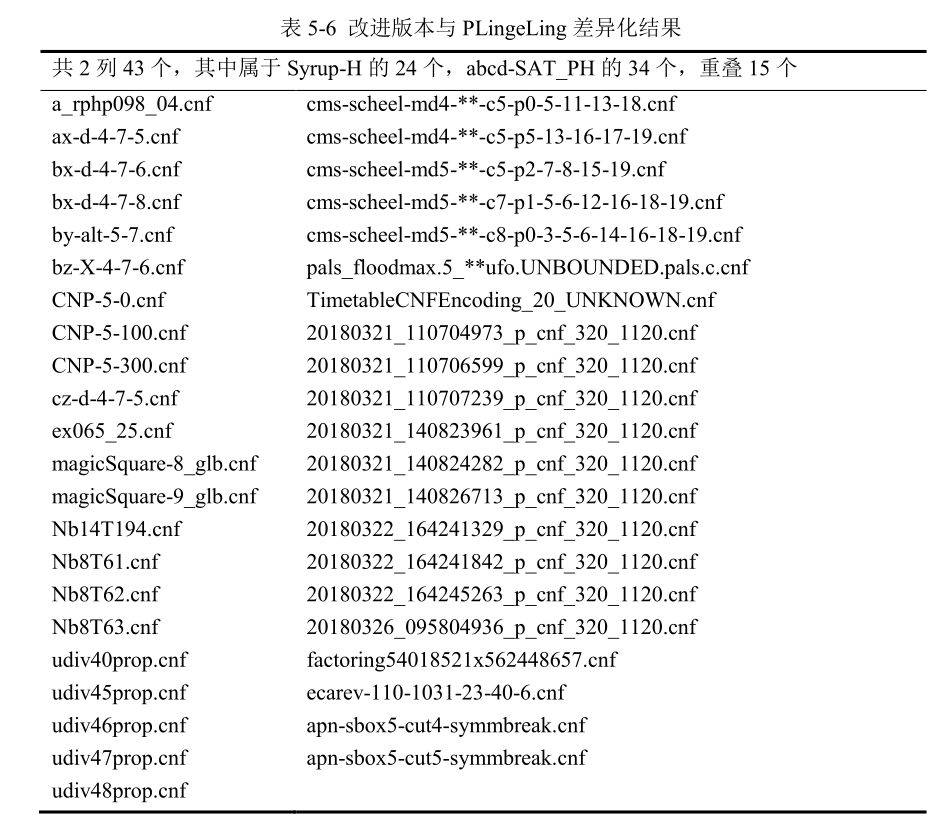
图 5-7 中原始版本用虚线表示,改进版本实线表示。从图中可以看出,采用混合评估算法后的版本均比原版本求解问题个数要多,且曲线形态上在原版本下方,表示用时更少。采用混合评估策略与子句共享策略的版本 Syrup-HE 表现不佳。其中与PLingeLing 最接近的版本是蓝色曲线代表的 abcd-SAT_PH,比 PLingeLing 少 6 个。但曲线形态呈现明显的 x 形,在交叉点位置,也即限时在 2200 秒之前,abcd-SAT_PH 曲线在 PLingeLing 下方,求解效率明显高于 PLingeLing。值得说明的是虽然 Syrup-H 与abcd-SAT_PH 比 PLingeLing 求解个数少。但其求解出了 PLingeLing 中未求解出的 43个问题(24,Syrup;34),列表如表 5-6 所示。
5.4 小结 本文采用混合学习子句评估算法对 glucose 的并行版本 syrup 进行改进。实验对比发现基于频次与 LBD 混合学习子句评估方式,在一定程度上能够达到并超过基于 LBD评估算法的 SAT 求解器的求解效率。 不足之处在于混合评估算法中的参数设置是基于统计分析得到,其内在关系还需要进一步研究。后续可以考虑针对具体的问题类型,分析学习子句使用频率与问题本身的关系,针对为题类型设置不同的参数以争取在规定时间内求解更多的问题。 |
|