二值观察相关文献

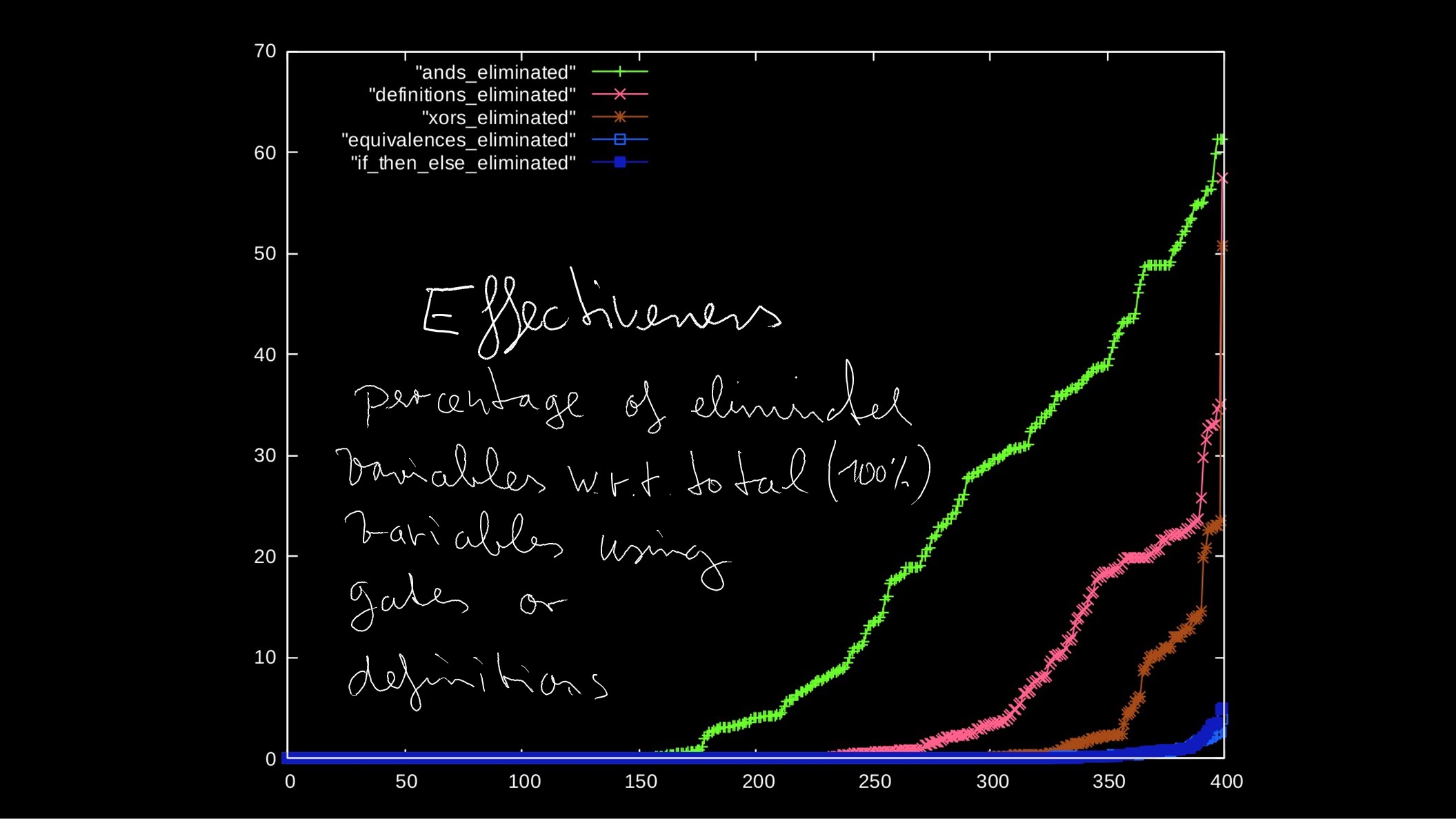
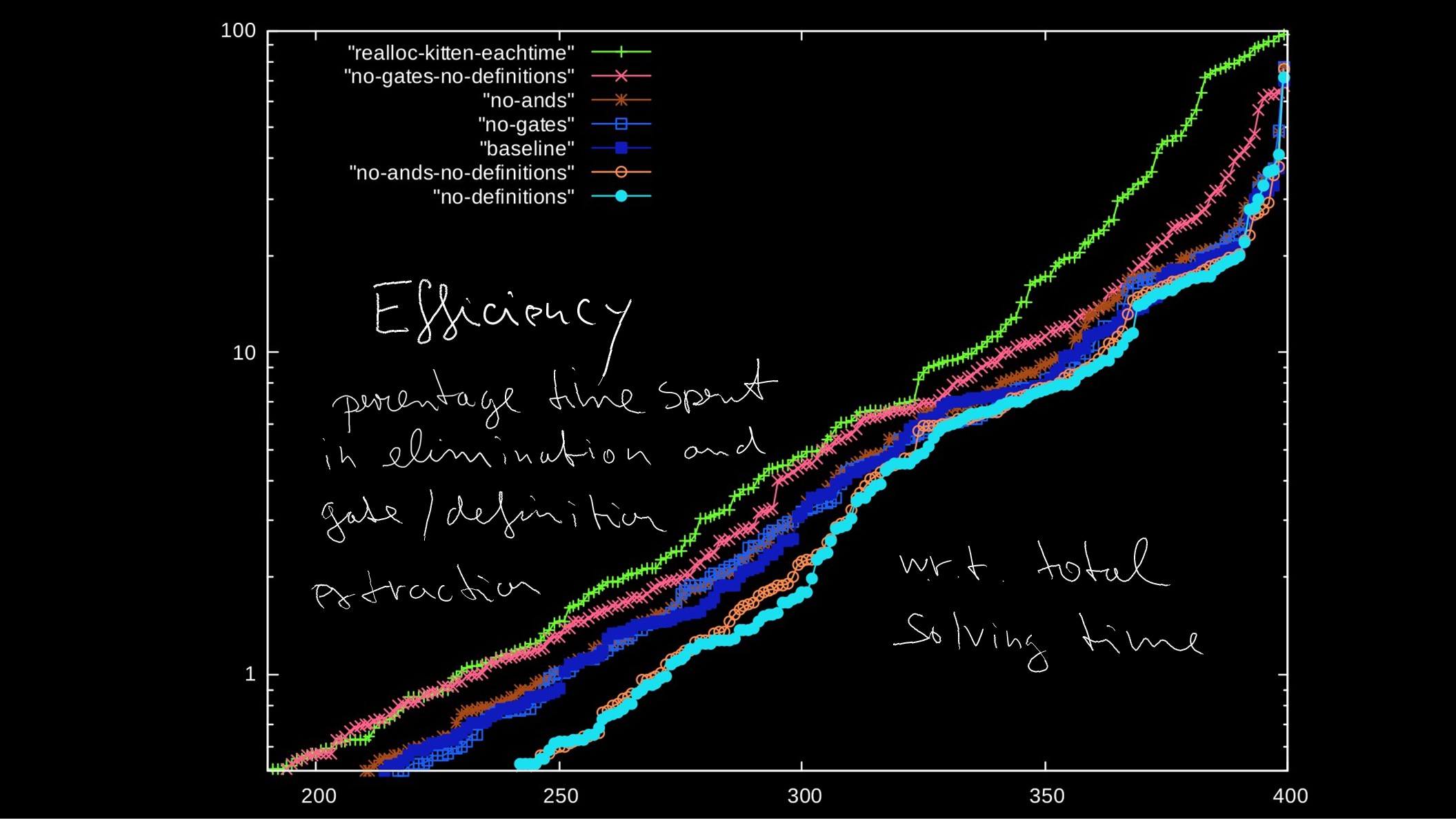
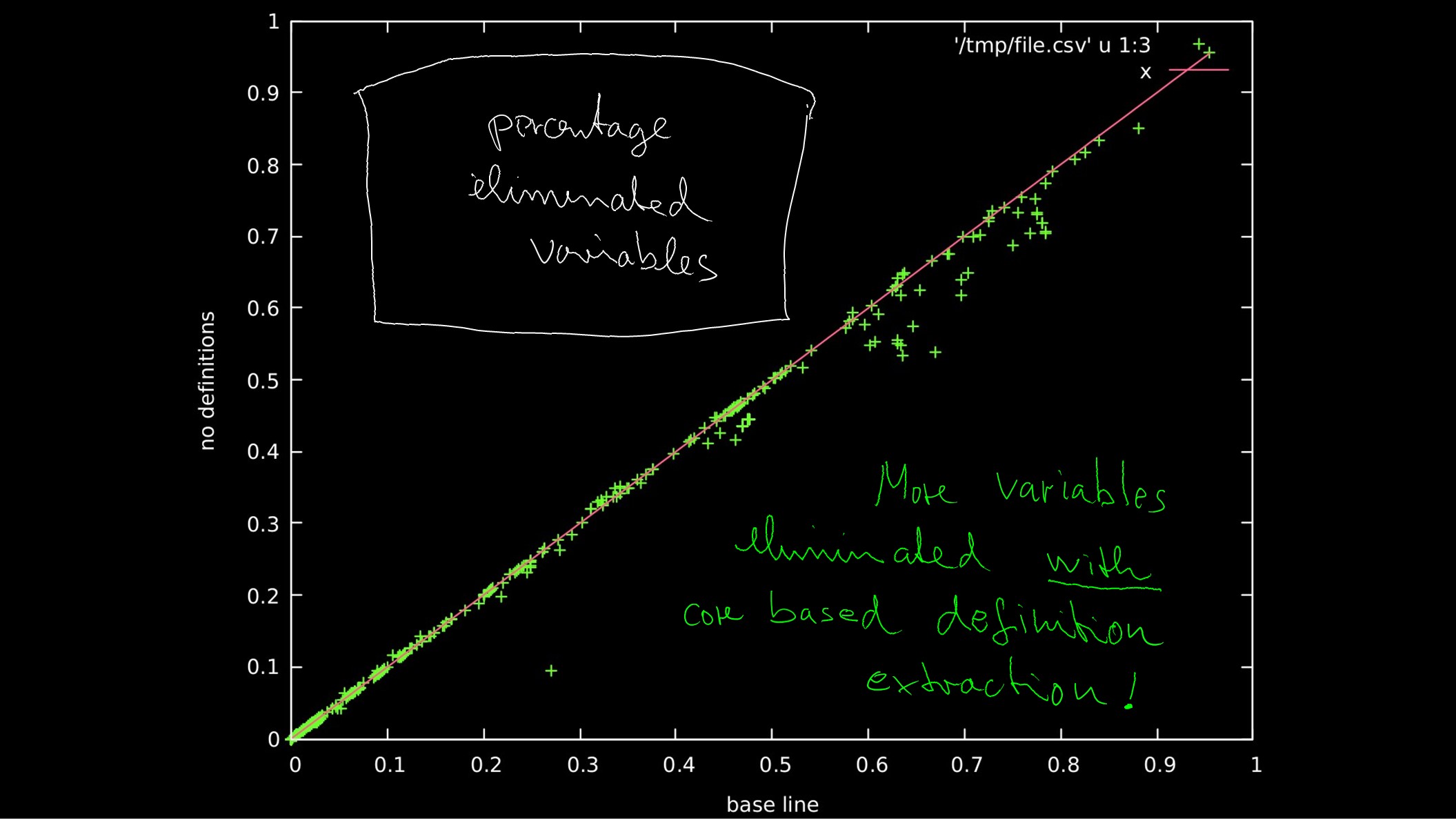
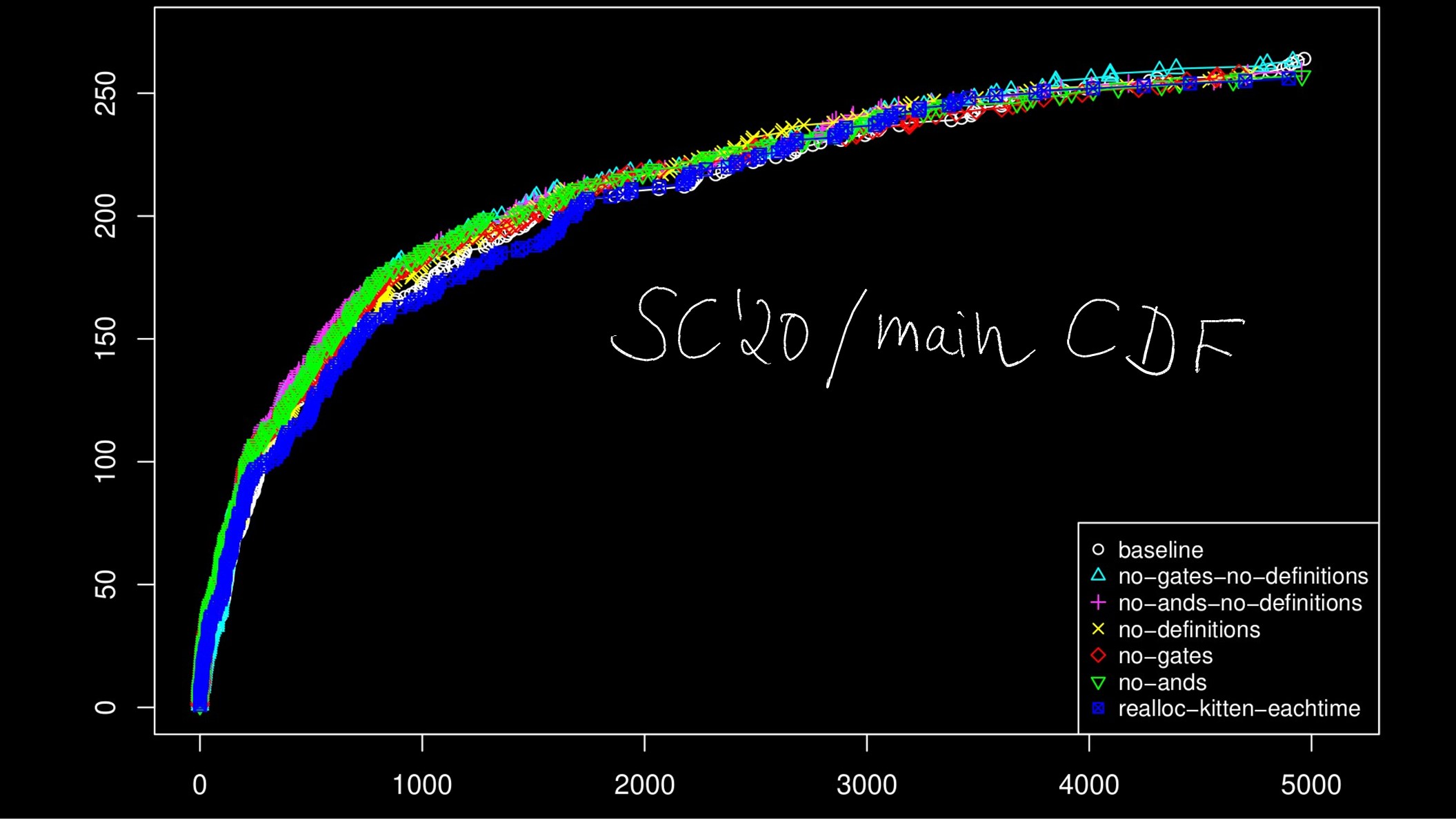
1.

 

Cadical 求解器propagate.cpp传播函数代码注释：

We are using the address of 'decision_reason' as pseudo reason for decisions to distinguish assignment decisions from other assignments.

Before we added chronological backtracking all learned units were assigned at decision level zero ('Solver.level == 0') and we just used a zero pointer as reason.

After allowing chronological backtracking units were also assigned at higher decision level (but with assignment level zero), and it was not possible anymore to just distinguish the case
'unit' versus 'decision' by just looking at the current level.

Both had a zero pointer as reason. Now only units have a zero reason and decisions need to use the pseudo reason 'decision_reason'.


This version of 'propagate' uses lazy watches and keeps two watched literals at the beginning of the clause.

We also use 'blocking literals' to reduce the number of times clauses have to be visited (2008 JSAT paper by Chu, Harwood and Stuckey).

——Cache Conscious Data Structures for Boolean Satisfiability Solvers
Chu, Geoffrey, Harwood, Aaron, and Stuckey, Peter J. ‘Cache Conscious Data Structures for Boolean Satisfiability Solvers’. 1 Jan. 2010 : 99 – 120.



The watches know if a watched clause is binary, in which case it never has to be visited. If a binary clause is falsified we continue propagating.

Finally, for long clauses we save the position of the last watch replacement in 'pos', which in turn reduces certain quadratic accumulated propagation costs (2013 JAIR article by Ian Gent) at the expense of four more bytes for each clause.
   
 

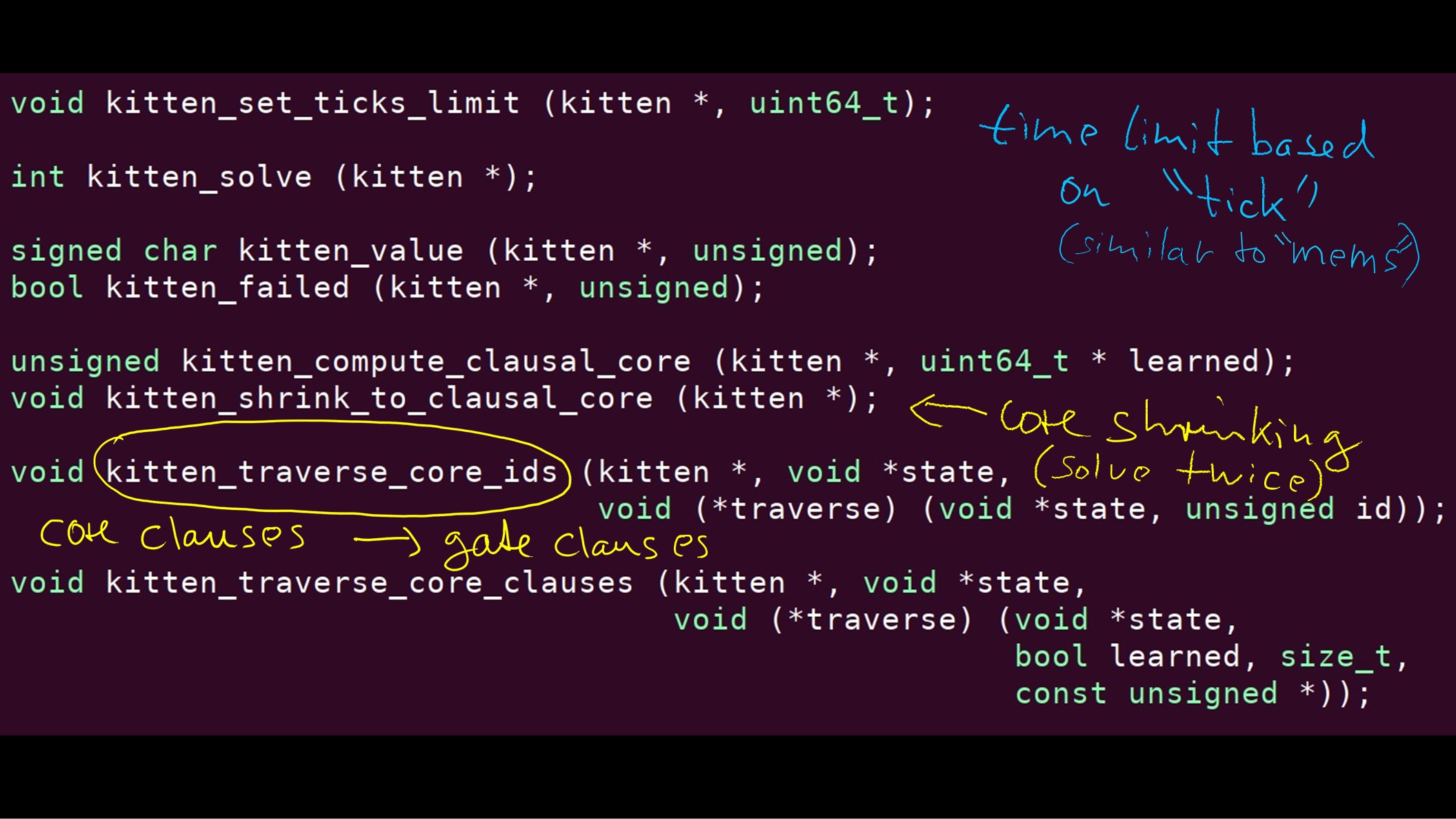
Cadical中组合有kitten求解器——主要利用kitten求解器的gate-eliminate技术

kitten求解器中有二值观察及propagate函数

 1 static inline unsigned 
 2 propagate_literal (kitten * kitten, unsigned lit)
 3 {
 4   LOG ("propagating %u", lit);
 5   value *values = kitten->values;
 6   assert (values[lit] > 0);
 7   const unsigned not_lit = lit ^ 1;
 8   katches *watches = kitten->watches + not_lit;
 9   unsigned conflict = INVALID;
10   unsigned *q = BEGIN_STACK (*watches);
11   const unsigned *const end_watches = END_STACK (*watches);
12   unsigned const *p = q;
13   while (conflict == INVALID && p != end_watches)
14     {
15       const unsigned ref = *q++ = *p++;
16       klause *c = dereference_klause (kitten, ref);
17       assert (c->size > 1);
18       unsigned *lits = c->lits;
19       const unsigned other = lits[0] ^ lits[1] ^ not_lit;
20       lits[0] = other, lits[1] = not_lit;
21       const value other_value = values[other];
22       if (other_value > 0)
23     continue;
24       value replacement_value = -1;
25       unsigned replacement = INVALID;
26       const unsigned *const end_lits = lits + c->size;
27       unsigned *r;
28       for (r = lits + 2; r != end_lits; r++)
29     {
30       replacement = *r;
31       replacement_value = values[replacement];
32       if (replacement_value >= 0)
33         break;
34     }
35       if (replacement_value >= 0)
36     {
37       assert (replacement != INVALID);
38       ROG (ref, "unwatching %u in", lit);
39       lits[1] = replacement;
40       *r = not_lit;
41       watch_klause (kitten, replacement, ref);
42       q--;
43     }
44       else if (other_value < 0)
45     {
46       ROG (ref, "conflict");
47       INC (kitten_conflicts);
48       conflict = ref;
49     }
50       else
51     {
52       assert (!other_value);
53       assign (kitten, other, ref);
54     }
55     }
56   while (p != end_watches)
57     *q++ = *p++;
58   SET_END_OF_STACK (*watches, q);
59   return conflict;
60 }
static inline unsigned propagate_literal (kitten * kitten, unsigned lit)
 1 static inline unsigned 
 2 propagate (kitten * kitten)
 3 {
 4   assert (kitten->inconsistent == INVALID);
 5   unsigned propagated = 0;
 6   unsigned conflict = INVALID;
 7   while (conflict == INVALID &&
 8      kitten->propagated < SIZE_STACK (kitten->trail))
 9     {
10       const unsigned lit = PEEK_STACK (kitten->trail, kitten->propagated);
11       conflict = propagate_literal (kitten, lit);
12       kitten->propagated++;
13       propagated++;
14     }
15   ADD (kitten_propagations, propagated);
16   return conflict;
17 }
static inline unsigned propagate (kitten * kitten)

 

kitten技术介绍——来自http://fmv.jku.at/biere/talks/Biere-POS21-talk.pdf

ppt1

 

ppt2

 

ppt3

 

ppt4

 

ppt5

 

ppt6

 

ppt7

 

ppt8

 

ppt9

 

ppt10

 

ppt11

 

ppt12

 

ppt13

 
   

2.

Cache Conscious Data Structures for Boolean Satisfiability Solvers
Chu, Geoffrey, Harwood, Aaron, and Stuckey, Peter J. ‘Cache Conscious Data Structures for Boolean Satisfiability Solvers’. 1 Jan. 2010 : 99 – 120.

3.

Ian P. Gent:
Optimal Implementation of Watched Literals and More General Techniques. J. Artif. Intell. Res. 48: 231-251 (2013)

4.

Martin Bromberger, Tobias Gehl, Lorenz Leutgeb, Christoph Weidenbach:

A Two-Watched Literal Scheme for First-Order Logic. PAAR@IJCAR 2022

 5. 最早期文献

[1] J. P. M. Silva, K. A. Sakallah, Grasp - a new search algorithm for satisfiability,
in: International Conference on Computer Aided Design, ICCAD, IEEE Computer
Society Press, 1996, pp. 220–227.

[2] M. W. Moskewicz, C. F. Madigan, Y. Zhao, L. Zhang, S. Malik, Chaff: Engineering
an efficient sat solver, in: Design Automation Conference, 2001. Proceedings, ACM,
2001, pp. 530–535.

6. 另一些文章title

A Two-Watched Literal Scheme for First-Order；

An efficient propositional prover;

Cache Conscious Data Structures for Boolean Satisfiability Solvers

Core First Unit Propagation

Improving Resource Unaware SAT Solvers

On the Glucose SAT Solver

Optimal Implementation of Watched Literals and More General Techniques

Optimal implementation of watched literals and more general

Watched Literals for Constraint Propagation in Minion

 

posted on 2023-02-10 16:34  海阔凭鱼跃越  阅读(30)  评论(0)  编辑  收藏  举报