样例生成、后处理与对应陷阱识别

 

这涉及一系列文献：

文献1：        Locality and Hard SAT-Instances  

                    ——Markström, Klas. ‘Locality and Hard SAT-Instances’. Journal on Satisfiability, Boolean Modeling and Computation, vol. 2, no. 1-4, pp. 221-227, 2006

 

求解器如何尝试避免这些实例所带来的至少一些陷阱。

	Abstract In this note we construct a family of SAT-instance based on Eulerian graphs which are aimed at being hard for resolution based SAT-solvers. We discuss some experiments made with instances of this type and how a solver can try to avoid at least some of the pitfalls presented by these instances. Finally we look at how the density of subformulae can influence the hardness of SAT instances. 我们将讨论使用这种类型的实例所做的一些实验，以及求解器如何尝试避免这些实例所带来的至少一些陷阱。
	1. Introduction DPLL method 这个方法实际上执行深度优先搜索，并结合单元子句的传播。 该方法是一个多项式时间复杂度，等价于树状归结。 Tree-like resolution is a fairly weak proof system and for a long time the performance of solvers were quite limited..树形归结是一种较弱的证明系统，长期以来求解器的性能都很有限。   树状归结弱于常规归结（包括many proper refinements of general resolution）和戴维斯-普特南归结。   The aim of this note is to construct a family of CNF formulae which are specially tuned to make use of the structure of current solvers to produce small hard examples. 这篇笔记的目的是构造一组CNF公式，这些公式是特别调整的，以利用当前求解器的结构来产生小的硬例子。 Several instances from the constructed family were submitted as benchmarks for the 2005 SAT solver competition, none of which could be solved by the competing solvers. 构建族中的几个实例被提交为2005年SAT求解器竞赛的基准，没有一个可以被竞争求解器解决。 In connection with this we will also give a short discussion of the importance of local dense subformulae for the performance of resolution based solvers.  与此相关，我们还将简要讨论局部密集子公式对基于分辨率的求解器性能的重要性。 Here we will also comment on some structural similarities between our family of formulae and formulae from the random k-SAT distribution. 在这里，我们还将评论我们的公式家族和随机k-SAT分布的公式之间的一些结构相似性。
	2. The problem class 图着色问题及其形式化方法   对应生成cnf的形式化方法实现 coloring.py #!/usr/bin/env python # -*- coding:utf-8 -*- """Formulas that encode coloring related problems """ from cnfgen.formula.cnf import CNF from cnfgen.graphs import Graph from cnfgen.localtypes import non_negative_int def GraphColoringFormula(G, colors, functional=True, formula_class=CNF): """Generates the clauses for colorability formula The formula encodes the fact that the graph :math:`G` has a coloring with color set ``colors``. This means that it is possible to assign one among the elements in ``colors``to that each vertex of the graph such that no two adjacent vertices get the same color. Parameters ---------- G : cnfgen.Graph a simple undirected graph colors : non negative int the number of colors functional: bool forbid a vertex to be mapped to multiple colors Returns ------- CNF the CNF encoding of the coloring problem on graph ``G`` """ non_negative_int(colors, 'colors') G = Graph.normalize(G, 'G') # Describe the formula description = "Graph {}-Colorability of {}".format(colors,G) F = formula_class(description=description) col = F.new_mapping(G.order(), colors,label='x_{{{0}{1}}}') # Color each vertex F.force_complete_mapping(col) if functional: F.force_functional_mapping(col) # This is a legal coloring for (v1, v2) in G.edges(): for c in range(1,colors+1): F.add_clause([-col(v1, c), -col(v2, c)]) return F def EvenColoringFormula(G, formula_class=CNF): """Even coloring formula The formula is defined on a graph :math:`G` and claims that it is possible to split the edges of the graph in two parts, so that each vertex has an equal number of incident edges in each part. The formula is defined on graphs where all vertices have even degree. The formula is satisfiable only on those graphs with an even number of edges in each connected component [1]_. Arguments --------- G : cnfgen.Graph a simple undirected graph where all vertices have even degree Raises ------ ValueError if the graph in input has a vertex with odd degree Returns ------- CNF object References ---------- .. [1] Locality and Hard SAT-instances, Klas Markstrom Journal on Satisfiability, Boolean Modeling and Computation 2 (2006) 221-228 """ G = Graph.normalize(G, 'G') description = "Even coloring formula on " + G.name F = formula_class(description=description) e = F.new_graph_edges(G) # Defined on both side for v in G.vertices(): if G.degree(v) % 2 == 1: raise ValueError( "Markstrom's Even Coloring formulas requires all\n vertices to have even degree." ) edge_vars = [e(u, v) for u,v in e.indices(v,None)] F.cardinality_eq(edge_vars, len(edge_vars) // 2) return F   cnf.py #!/usr/bin/env python # -*- coding:utf-8 -*- """Build and manipulate CNF formulas The module `contains facilities to generate cnf formulas, in order to be printed in DIMACS, OPB or LaTeX formats. Such formulas are ready to be fed to sat solvers. The module implements the `CNF` object, which is the main entry point to the `cnfgen` library. Copyright (C) 2012-2022 Massimo Lauria <lauria.massimo@gmail.com> https://github.com/MassimoLauria/cnfgen.git """ from cnfgen.formula.cnfio import CNFio from cnfgen.formula.linear import CNFLinear from cnfgen.formula.variables import VariablesManager class CNF(VariablesManager, CNFio, CNFLinear): """Propositional formulas in conjunctive normal form. A CNF formula is a sequence of clauses, which are sequences of literals. Each literal is either a variable or its negation. Use ``add_clause`` to add new clauses to CNF. Clauses will be added multiple times in case of multiple insertion of the same clauses. For documentation purpose it is possible use have an additional comment header at the top of the formula, which will be *optionally* exported to LaTeX or dimacs. Implementation: for efficiency reason clauses and variable can only be added, and not deleted. Furthermore order matters in the representation. Examples -------- >>> c=CNF([[1, 2, -3], [-2, 4]]) >>> print( c.to_dimacs(),end='') p cnf 4 2 1 2 -3 0 -2 4 0 >>> c.add_clause([-3, 4, -5]) >>> print( c.to_dimacs(),end='') p cnf 5 3 1 2 -3 0 -2 4 0 -3 4 -5 0 >>> print(c[1]) [-2, 4] """ def __init__(self, clauses=None, description=None): """Propositional formulas in conjunctive normal form. Parameters ---------- clauses : ordered list of clauses a clause with k literals list containing k pairs, each representing a literal (see `add_clause`). First element is the polarity and the second is the variable, which must be an hashable object. E.g. (not x3) or x4 or (not x2) is encoded as [(False,"x3"),(True,"x4"),False,"x2")] description: string, optional a description of the formula """ CNFLinear.__init__(self, clauses=clauses, description=description) VariablesManager.__init__(self,self)   #!/usr/bin/env python # -*- coding:utf-8 -*- """Utilities to manage graph formats and graph files in order to build formulas that are graph based. """ import os import io import random from io import StringIO import copy from bisect import bisect_right, bisect_left import networkx from cnfgen.localtypes import positive_int, non_negative_int __all__ = [ "readGraph", "writeGraph", "Graph", "DirectedGraph", "BipartiteGraph", "supported_graph_formats", "bipartite_random_left_regular", "bipartite_random_regular", "bipartite_random_m_edges", "bipartite_random", "dag_complete_binary_tree", "dag_pyramid", "dag_path" ] ################################################################# # Import third party code ################################################################# class BipartiteEdgeList(): """Edge list for bipartite graphs""" def __init__(self, B): self.B = B def __len__(self): return self.B.number_of_edges() def __contains__(self, t): return len(t) == 2 and self.B.has_edge(t[0], t[1]) def __iter__(self): for u in range(1, self.B.left_order() + 1): yield from ((u, v) for v in self.B.right_neighbors(u)) class GraphEdgeList(): """Edge list for bipartite graphs""" def __init__(self, G): self.G = G def __len__(self): return self.G.number_of_edges() def __contains__(self, t): return len(t) == 2 and self.G.has_edge(t[0], t[1]) def __iter__(self): n = self.G.number_of_vertices() G = self.G for u in range(1, n): pos = bisect_right(G.adjlist[u], u) while pos < len(G.adjlist[u]): v = G.adjlist[u][pos] yield (u, v) pos += 1 class DirectedEdgeList(): """Edge list for bipartite graphs""" def __init__(self, D, sort_by_predecessors=True): self.D = D self.sort_by_pred = sort_by_predecessors def __len__(self): return self.D.number_of_edges() def __contains__(self, t): return len(t) == 2 and self.D.has_edge(t[0], t[1]) def __iter__(self): n = self.D.number_of_vertices() if self.sort_by_pred: successors = self.D.succ for src in range(1, n+1): for dest in successors[src]: yield (src, dest) else: predecessors = self.D.pred for dest in range(1, n+1): for src in predecessors[dest]: yield (src, dest) class BaseGraph(): """Base class for graphs""" def is_dag(self): """Test whether the graph is directed acyclic This is not a full test. It only checks that all directed edges (u,v) have that u < v.""" raise NotImplementedError def is_directed(self): "Test whether the graph is directed" raise NotImplementedError def is_multigraph(self): "Test whether the graph can have multi-edges" return False def is_bipartite(self): "Test whether the graph is a bipartite object" return False def order(self): return self.number_of_vertices() def vertices(self): return range(1, self.number_of_vertices()+1) def number_of_vertices(self): raise NotImplementedError def number_of_edges(self): raise NotImplementedError def has_edge(self, u, v): raise NotImplementedError def add_edge(self, u, v): raise NotImplementedError def add_edges_from(self, edges): for u, v in edges: self.add_edge(u, v) def edges(self): raise NotImplementedError def __len__(self): return self.number_of_vertices() def to_networkx(self): """Convert the graph TO a networkx object.""" raise NotImplementedError @classmethod def from_networkx(cls, G): """Create a graph object from a networkx graph""" raise NotImplementedError @classmethod def normalize(cls, G): """Guarantees a cnfgen graph object""" raise NotImplementedError @classmethod def supported_file_formats(cls): """File formats supported for graph I/O""" raise NotImplementedError @classmethod def graph_type_name(cls): """File formats supported for graph I/O""" raise NotImplementedError @classmethod def from_file(cls, fileorname, fileformat=None): """Load the graph from a file The file format is either indicated in the `fileformat` variable or, if that is `None`, or from the extension of the filename. Parameters ----------- fileorname: str or file-like object the input file from which the graph is read. If it is a string then the graph is read from a file with that string as filename. Otherwise if the fileorname is a file object (or a text stream), the graph is read from there. Input files are assumed to be UTF-8 by default (for some formats it is actually ascii) fileformat: string, optional The file format that the parser should expect to receive. See also :py:func:`cnfgen.graph.supported_formats`. By default it tries to autodetect it from the file name extension (when applicable).""" # Reduce to the case of filestream if isinstance(fileorname, str): with open(fileorname, 'r', encoding='utf-8') as file_handle: return cls.from_file(file_handle, fileformat) # Discover and test file format fileformat = guess_fileformat(fileorname, fileformat) allowed = cls.supported_file_formats() typename = cls.graph_type_name() if fileformat not in allowed: raise ValueError( "Invalid file type." " For {} graphs we support {}".format(typename, allowed)) # Read file return readGraph(fileorname, typename, fileformat) class Graph(BaseGraph): def is_dag(self): return False def is_directed(self): return False def __init__(self, n, name=None): non_negative_int(n, 'n') self.n = n self.m = 0 self.adjlist = [[] for i in range(n+1)] self.edgeset = set() if name is None: self.name = "a simple graph with {} vertices".format(n) else: self.name = name def add_edge(self, u, v): if not (1 <= u <= self.n and 1 <= v <= self.n and u != v): raise ValueError( "u,v must be distinct, between 1 and the number of nodes") if (u, v) in self.edgeset: return u, v = min(u, v), max(u, v) pos = bisect_right(self.adjlist[u], v) self.adjlist[u].insert(pos, v) pos = bisect_right(self.adjlist[v], u) self.adjlist[v].insert(pos, u) self.m += 1 self.edgeset.add((u, v)) self.edgeset.add((v, u)) def update_vertex_number(self, new_value): """Raises the number of vertices to `new_value`""" non_negative_int(new_value, 'new_value') for _ in range(self.n,new_value): self.adjlist.append([]) self.n = max(self.n, new_value) def remove_edge(self,u,v): if not self.has_edge(u,v): return self.edgeset.remove((u,v)) self.edgeset.remove((v,u)) self.adjlist[u].remove(v) self.adjlist[v].remove(u) self.m -= 1 def has_edge(self, u, v): return (u, v) in self.edgeset def vertices(self): return range(1, self.n+1) def edges(self): """Outputs all edges in the graph""" return GraphEdgeList(self) def number_of_vertices(self): return self.n def number_of_edges(self): return self.m def to_networkx(self): G = networkx.Graph() G.add_nodes_from(range(1, self.n+1)) G.add_edges_from(self.edges()) return G def neighbors(self, u): """Outputs the neighbors of vertex `u` The sequence of neighbors is guaranteed to be sorted. """ if not(1 <= u <= self.n): raise ValueError("vertex u not in the graph") yield from self.adjlist[u] def degree(self, u): if not(1 <= u <= self.n): raise ValueError("vertex u not in the graph") return len(self.adjlist[u]) @classmethod def from_networkx(cls, G): if not isinstance(G, networkx.Graph): raise ValueError('G is expected to be of type networkx.Graph') G = normalize_networkx_labels(G) C = cls(G.order()) C.add_edges_from(G.edges()) try: C.name = G.name except AttributeError: C.name = '<unknown graph>' return C @classmethod def graph_type_name(cls): """Simple graphs are laleled as 'simple'""" return 'simple' @classmethod def supported_file_formats(cls): """File formats supported for simple graph I/O""" # Check that DOT is a supported format if has_dot_library(): return ['kthlist', 'gml', 'dot', 'dimacs'] else: return ['kthlist', 'gml', 'dimacs'] @classmethod def null_graph(cls): return cls(0, 'the null graph') @classmethod def empty_graph(cls, n): return cls(n, 'the empty graph of order '+str(n)) @classmethod def complete_graph(cls, n): G = cls(n, 'the complete graph of order '+str(n)) for u in range(1, n): for v in range(u+1, n+1): G.add_edge(u, v) return G @classmethod def star_graph(cls, n): G = cls(n+1, 'the star graph with {} arms'.format(n)) for u in range(1, n+1): G.add_edge(u, n+1) return G @classmethod def normalize(cls, G, varname=''): """Guarantees a cnfgen.graphs.Graph object If the given graph `G` is a networkx.Graph object, this method produces a CNFgen simple graph object, relabeling vertices so that vertices are labeled as numbers from 1 to `n`, where `n` is the number of vertices in `G`. If the vertices in the original graph have some kind of order, the order is preserved. If `G` is already a `cnfgen.graphs.Graph` object, nothing is done. Parameters ---------- cls: a class G : networkx.Graph or cnfgen.Graph the graph to normalize/check varname: str the variable name, for error messages (default: 'G') """ typemsg = "type of argument '{}' must be either networx.Graph or cnfgen.Graph" conversionmsg = "cannot convert '{}' into a cnfgen.Graph object" if not isinstance(G, (Graph, networkx.Graph)): raise TypeError(typemsg.format(varname)) if isinstance(G, Graph): return G try: G2 = cls.from_networkx(G) return G2 except AttributeError: raise ValueError(conversionmsg.format(varname)) class DirectedGraph(BaseGraph): def is_dag(self): """Is the graph acyclic? The vertices in the graph are assumed to be topologically sorted, therefore this function just determines whether there are edges going backward with respect to this order, which can be done in O(1) because edges can be added and not removed.""" return self.still_a_dag def is_directed(self): return True def __init__(self, n, name='a simple directed graph'): non_negative_int(n, 'n') self.n = n self.m = 0 self.edgeset = set() self.still_a_dag = True self.pred = [[] for i in range(n+1)] self.succ = [[] for i in range(n+1)] if name is None: self.name = "a directed graph with {} vertices".format(n) else: self.name = name def add_edge(self, src, dest): if not (1 <= src <= self.n and 1 <= dest <= self.n): raise ValueError( "u,v must be distinct, between 1 and the number of nodes") if self.has_edge(src, dest): return if src >= dest: self.still_a_dag = False pos = bisect_right(self.pred[dest], src) self.pred[dest].insert(pos, src) pos = bisect_right(self.succ[src], dest) self.succ[src].insert(pos, dest) self.m += 1 self.edgeset.add((src, dest)) def has_edge(self, src, dest): """True if graph contains directed edge (src,dest)""" return (src, dest) in self.edgeset def vertices(self): return range(1, self.n+1) def edges(self): return DirectedEdgeList(self) def edges_ordered_by_successors(self): return DirectedEdgeList(self, sort_by_predecessors=False) def number_of_vertices(self): return self.n def number_of_edges(self): return self.m def to_networkx(self): G = networkx.DiGraph() G.add_nodes_from(range(1, self.n+1)) G.add_edges_from(self.edges()) return G def predecessors(self, u): """Outputs the predecessors of vertex `u` The sequence of predecessors is guaranteed to be sorted.""" if not(1 <= u <= self.n): raise ValueError("vertex u not in the graph") yield from self.pred[u] def successors(self, u): """Outputs the successors of vertex `u` The sequence of successors is guaranteed to be sorted.""" if not(1 <= u <= self.n): raise ValueError("vertex u not in the graph") yield from self.succ[u] def in_degree(self, u): if not(1 <= u <= self.n): raise ValueError("vertex u not in the graph") return len(self.pred[u]) def out_degree(self, v): if not(1 <= v <= self.n): raise ValueError("vertex v not in the graph") return len(self.succ[v]) @classmethod def from_networkx(cls, G): if not isinstance(G, networkx.DiGraph): raise ValueError('G is expected to be of type networkx.DiGraph') G = normalize_networkx_labels(G) C = cls(G.order()) C.add_edges_from(G.edges()) try: C.name = G.name except AttributeError: C.name = '<unknown graph>' return C @classmethod def graph_type_name(cls): """Directed graphs are laleled as 'digraph'""" return 'digraph' @classmethod def supported_file_formats(cls): """File formats supported for directed graph I/O""" if has_dot_library(): return ['kthlist', 'gml', 'dot', 'dimacs'] else: return ['kthlist', 'gml', 'dimacs'] @classmethod def normalize(cls, G, varname='G'): """Guarantees a cnfgen.graphs.DirerctedGraph object If the given graph `G` is a networkx.DiGraph object, this method produces a CNFgen directed graph object, relabeling vertices so that vertices are labeled as numbers from 1 to `n`, where `n` is the number of vertices in `G`. If the vertices in the original graph have some kind of order, the order is preserved. If all edges go from lower vertices to higher vertices, with respect to the labeling, then t he graph is considered a directed acyclic graph DAG. If `G` is already a `cnfgen.graphs.DirectedGraph` object, nothing is done. Parameters ---------- cls: a class G : networkx.DiGraph or cnfgen.DirectedGraph the graph to normalize/check varname: str the variable name, for error messages (default: 'G') """ typemsg = "type of argument '{}' must be either networx.DiGraph or cnfgen.DirectedGraph" conversionmsg = "cannot convert '{}' into a cnfgen.DirectedGraph object" if not isinstance(G, (DirectedGraph, networkx.DiGraph)): raise TypeError(typemsg.format(varname)) if isinstance(G, DirectedGraph): return G try: G2 = cls.from_networkx(G) return G2 except AttributeError: raise ValueError(conversionmsg.format(varname)) class BaseBipartiteGraph(BaseGraph): """Base class for bipartite graphs""" def __init__(self, L, R, name=None): non_negative_int(L, 'L') non_negative_int(R, 'R') self.lorder = L self.rorder = R if name is None: self.name = 'a bipartite graph with ({},{}) vertices'.format(L, R) else: self.name = name def is_bipartite(self): return True def number_of_vertices(self): return self.lorder + self.rorder def edges(self): return BipartiteEdgeList(self) def left_order(self): return self.lorder def right_order(self): return self.rorder def left_degree(self, v): return len(self.left_neighbors(v)) def right_degree(self, u): return len(self.right_neighbors(u)) def left_neighbors(self, v): raise NotImplementedError def right_neighbors(self, u): raise NotImplementedError def parts(self): return range(1, self.lorder + 1), range(1, self.rorder + 1) def to_networkx(self): G = networkx.Graph() n, m = self.lorder, self.rorder G.add_nodes_from(range(1, n+1), bipartite=0) G.add_nodes_from(range(n+1, m+n+1), bipartite=1) G.add_edges_from((u, v+n) for (u, v) in self.edges()) G.name = self.name return G class BipartiteGraph(BaseBipartiteGraph): def __init__(self, L, R, name=None): non_negative_int(L, 'L') non_negative_int(R, 'R') BaseBipartiteGraph.__init__(self, L, R, name) self.ladj = {} self.radj = {} self.edgeset = set() def has_edge(self, u, v): return (u, v) in self.edgeset def add_edge(self, u, v): """Add an edge to the graph. - multi-edges are not allowed - neighbors of a vertex are kept in numberic order Examples -------- >>> G = BipartiteGraph(3,5) >>> G.add_edge(2,3) >>> G.add_edge(2,2) >>> G.add_edge(2,3) >>> G.right_neighbors(2) [2, 3] """ if not (1 <= u <= self.lorder and 1 <= v <= self.rorder): raise ValueError("Invalid choice of vertices") if (u, v) in self.edgeset: return if u not in self.ladj: self.ladj[u] = [] if v not in self.radj: self.radj[v] = [] pv = bisect_right(self.ladj[u], v) pu = bisect_right(self.radj[v], u) self.ladj[u].insert(pv, v) self.radj[v].insert(pu, u) self.edgeset.add((u, v)) def number_of_edges(self): return len(self.edgeset) def right_neighbors(self, u): """Outputs the neighbors of a left vertex `u` The sequence of neighbors is guaranteed to be sorted.""" if not (1 <= u <= self.lorder): raise ValueError("Invalid choice of vertex") return self.ladj.get(u, [])[:] def left_neighbors(self, v): """Outputs the neighbors of right vertex `u` The sequence of neighbors is guaranteed to be sorted.""" if not (1 <= v <= self.rorder): raise ValueError("Invalid choice of vertex") return self.radj.get(v, [])[:] @classmethod def from_networkx(cls, G): """Convert a :py:class:`networkx.Graph` into a :py:class:`cnfgen.graphs.BipartiteGraph` In order to convert a :py:class:`networkx.Graph` object `G`, it is necessary that all nodes in `G` have the property `bipartite` set to either `0` or `1`. If this is not the case, or if there are edges between the two parts, :py:class:`ValueError` is raised. Example ------- >>> G = networkx.bipartite.complete_bipartite_graph(5,7) >>> B = BipartiteGraph.from_networkx(G) >>> print(B.order()) 12 >>> print(B.left_order()) 5 >>> print(B.has_edge(2,3)) True """ if not isinstance(G, networkx.Graph): raise ValueError('G is expected to be of type networkx.Graph') side = [[], []] index = [{}, {}] for u in G.nodes(): try: color = G.nodes[u]['bipartite'] assert color in ['0', 0, '1', 1] except (KeyError, AssertionError): raise ValueError( "Node {} lacks the 'bipartite' property set to 0 or 1".format(u)) side[int(color)].append(u) B = cls(len(side[0]), len(side[1])) index[0] = {u: i for (i, u) in enumerate(side[0], start=1)} index[1] = {v: i for (i, v) in enumerate(side[1], start=1)} for u, v in G.edges(): ucolor = 0 if (u in index[0]) else 1 vcolor = 1 if (v in index[1]) else 0 if ucolor == vcolor: raise ValueError( "Edge ({},{}) across the bipartition".format(u, v)) iu, iv = index[ucolor][u], index[vcolor][v] if ucolor == 0: B.add_edge(iu, iv) else: B.add_edge(iv, iu) try: B.name = G.name except AttributeError: B.name = '<unknown graph>' return B @classmethod def graph_type_name(cls): """Bipartite graphs are laleled as 'bipartite'""" return 'bipartite' @classmethod def supported_file_formats(cls): """File formats supported for bipartite graph I/O""" if has_dot_library(): return ['kthlist', 'gml', 'dot', 'matrix'] else: return ['kthlist', 'gml', 'matrix'] @classmethod def normalize(cls, G, varname='G'): """Guarantees a cnfgen.graphs.BipartiteGraph object If the given graph `G` is a networkx.Graph object with a bipartition, this method produces a CNFgen bipartite graph object, relabeling vertices so that vertices og each side are labeled as numbers from 1 to `n` and 1 to `m` respectively, where `n` and `m` are the numbers of vertices in `G` on the left and right side, respectively. If the vertices in the original graph have some kind of order, the order is preserved. If `G` is already a `cnfgen.graphs.BipartiteGraph` object, nothing is done. """ typemsg = "type of argument '{}' must be either networx.Graph or cnfgen.BipartiteGraph" conversionmsg = "cannot convert '{}' to a bipartite graph: inconsistent 'bipartite' labeling" if not isinstance(G, (BipartiteGraph, networkx.Graph)): raise TypeError(typemsg.format(varname)) if isinstance(G, BipartiteGraph): return G try: G2 = cls.from_networkx(G) return G2 except AttributeError: raise ValueError(conversionmsg.format(varname)) class CompleteBipartiteGraph(BipartiteGraph): def __init__(self, L, R): BipartiteGraph.__init__(self, L, R) self.name = 'Complete bipartite graph with ({},{}) vertices'.format( L, R) def has_edge(self, u, v): return (1 <= u <= self.lorder and 1 <= v <= self.rorder) def add_edge(self, u, v): pass def number_of_edges(self): return self.lorder * self.rorder def right_neighbors(self, u): return range(1, self.rorder + 1) def left_neighbors(self, v): return range(1, self.lorder + 1) def has_dot_library(): """Test the presence of pydot """ try: # newer version of networkx from networkx import nx_pydot import pydot del pydot return True except ImportError: pass return False ################################################################# # Graph reader/writer ################################################################# def guess_fileformat(fileorname, fileformat=None): """Guess the file format for the file or filename """ if fileformat is not None: return fileformat try: if isinstance(fileorname, str): name = fileorname else: name = fileorname.name return os.path.splitext(name)[-1][1:] except (AttributeError, ValueError, IndexError): raise ValueError( "Cannot guess a file format from arguments. Please specify the format manually.") def _process_graph_io_arguments(iofile, graph_type, file_format, multi_edges): """Test if the argument for the graph I/O functions make sense""" # Check the file if not isinstance(iofile, io.TextIOBase) and \ not isinstance(iofile, io.IOBase) and \ not isinstance(iofile, StringIO): raise ValueError( "The IO stream \"{}\" does not correspond to a file".format( iofile)) # Check the graph type specification if graph_type not in ['dag', 'digraph', 'simple', 'bipartite']: raise ValueError("The graph type must be one of " + list(_graphformats.keys())) if multi_edges: raise NotImplementedError("Multi edges not supported yet") elif graph_type in ["dag", "digraph"]: grtype = DirectedGraph elif graph_type == "simple": grtype = Graph elif graph_type == "bipartite": grtype = BipartiteGraph else: raise RuntimeError( "Unknown graph type argument: {}".format(graph_type)) # Check/discover file format specification if file_format == 'autodetect': try: extension = os.path.splitext(iofile.name)[-1][1:] except AttributeError: raise ValueError( "Cannot guess a file format from an IO stream with no name. Please specify the format manually." ) if extension not in grtype.supported_file_formats(): raise ValueError("Cannot guess a file format for {} graphs from the extension of \"{}\". Please specify the format manually.". format(graph_type, iofile.name)) else: file_format = extension elif file_format not in grtype.supported_file_formats(): raise ValueError( "For {} graphs we only support these formats: {}".format( graph_type, grtype.supported_file_formats())) return (grtype, file_format) def normalize_networkx_labels(G): """Relabel all vertices as integer starting from 1""" # Normalize GML file. All nodes are integers starting from 1 try: G = networkx.convert_node_labels_to_integers( G, first_label=1, ordering='sorted') except TypeError: # Ids cannot be sorted natively G = networkx.convert_node_labels_to_integers( G, first_label=1, ordering='default') return G def readGraph(input_file, graph_type, file_format='autodetect', multi_edges=False): """Read a Graph from file In the case of "bipartite" type, the graph obtained is of :py:class:`cnfgen.graphs.BipartiteGraph`. In the case of "simple" type, the graph is obtained of :py:class:`cnfgen.graphs.Graph`. In the case of "dag" or "directed" type, the graph obtained is of :py:class:`cnfgen.graphs.DirectedGraph`. The supported file formats are enumerated by the respective class method ``supported_file_formats`` In the case of "dag" type, the graph read in input must have increasing edges, in the sense that all edges must be such that the source has lower identifier than the sink. (I.e. the numeric identifiers of the vertices are a topological order for the graph) Parameters ----------- input_file: str or file-like object the input file from which the graph is read. If it is a string then the graph is read from a file with that string as filename. Otherwise if the input_file is a file object (or a text stream), the graph is read from there. Input files are assumed to be UTF-8 by default. graph_type: string in {"simple","digraph","dag","bipartite"} file_format: string, optional The file format that the parser should expect to receive. See also the method py:method::``supported_file_formats``. By default it tries to autodetect it from the file name extension (when applicable). multi_edges: bool,optional are multiple edge allowed in the graph? By default this is not allowed. Returns ------- a graph object one type among Graph, DirectedGraph, BipartiteGraph Raises ------ ValueError raised when either ``input_file`` is neither a file object nor a string, or when ``graph_type`` and ``file_format`` are invalid choices. IOError it is impossible to read the ``input_file`` See Also -------- writeGraph, is_dag, has_bipartition """ if multi_edges: raise NotImplementedError("Multi edges not supported yet") # file name instead of file object if isinstance(input_file, str): with open(input_file, 'r', encoding='utf-8') as file_handle: return readGraph(file_handle, graph_type, file_format, multi_edges) graph_class, file_format = _process_graph_io_arguments(input_file, graph_type, file_format, multi_edges) if file_format == 'dot': # This is a workaround. In theory a broken dot file should # cause a pyparsing.ParseError but the dot_reader used by # networkx seems to mismanage that and to cause a TypeError # try: G = networkx.nx_pydot.read_dot(input_file) try: # work around for a weird parse error in pydot, which # adds an additiona vertex '\\n' in the graph. G.remove_node('\\n') except networkx.exception.NetworkXError: pass G = graph_class.normalize(G) except TypeError: raise ValueError('Parse Error in dot file') elif file_format == 'gml': # Networkx's GML reader expects to read from ascii encoded # binary file. We could have sent the data to a temporary # binary buffer but for some reasons networkx's GML reader # function is poorly written and does not like such buffers. # It turns out we can pass the data as a list of # encoded ascii lines. # # The 'id' field in the vertices are supposed to be an integer # and will be used as identifiers for the vertices in Graph # object too. # try: G = networkx.read_gml((line.encode('ascii') for line in input_file), label='id') G = graph_class.normalize(G) except networkx.NetworkXError as errmsg: raise ValueError("[Parse error in GML input] {} ".format(errmsg)) except UnicodeEncodeError as errmsg: raise ValueError( "[Non-ascii chars in GML file] {} ".format(errmsg)) elif file_format == 'kthlist' and graph_type == 'bipartite': G = _read_bipartite_kthlist(input_file) elif file_format == 'kthlist' and graph_type != 'bipartite': G = _read_nonbipartite_kthlist(input_file, graph_class) elif file_format == 'dimacs': G = _read_graph_dimacs_format(input_file, graph_class) elif file_format == 'matrix': G = _read_graph_matrix_format(input_file) else: raise RuntimeError( "[Internal error] Format {} not implemented".format(file_format)) if graph_type == "dag" and not G.is_dag(): raise ValueError( "[Input error] Graph must be explicitly acyclic (src->dest edges where src<dest)") return G def writeGraph(G, output_file, graph_type, file_format='autodetect'): """Write a graph to a file Parameters ----------- G : BaseGraph output_file: file object the output file to which the graph is written. If it is a string then the graph is written to a file with that string as filename. Otherwise if ``output_file`` is a file object (or a text stream), the graph is written there. The file is written in UTF-8 by default. graph_type: string in {"simple","digraph","dag","bipartite"} see also :py:func:`cnfgen.graph.supported_formats` file_format: string, optional The file format that the parser should expect to receive. See also :py:func:`cnfgen.graph.supported_formats`. By default it tries to autodetect it from the file name extension (when applicable). Returns ------- None Raises ------ ValueError raised when either ``output_file`` is neither a file object nor a string, or when ``graph_type`` and ``file_format`` are invalid choices. IOError it is impossible to write on the ``output_file`` See Also -------- readGraph """ if not isinstance(G, BaseGraph): raise TypeError("G must be a cnfgen.graphs.BaseGraph") # file name instead of file object if isinstance(output_file, str): with open(output_file, 'w', encoding='utf-8') as file_handle: return writeGraph(G, file_handle, graph_type, file_format) _, file_format = _process_graph_io_arguments(output_file, graph_type, file_format, False) if file_format == 'dot': G = G.to_networkx() networkx.nx_pydot.write_dot(G, output_file) elif file_format == 'gml': # Networkx's GML writer expects to write to an ascii encoded # binary file. Thus we need to let Networkx write to # a temporary binary ascii encoded buffer and then convert the # content before sending it to the output file. tempbuffer = io.BytesIO() G = G.to_networkx() networkx.write_gml(G, tempbuffer) print(tempbuffer.getvalue().decode('ascii'), file=output_file) elif file_format == 'kthlist' and graph_type != 'bipartite': _write_graph_kthlist_nonbipartite(G, output_file) elif file_format == 'kthlist' and graph_type == 'bipartite': _write_graph_kthlist_bipartite(G, output_file) elif file_format == 'dimacs': _write_graph_dimacs_format(G, output_file) elif file_format == 'matrix': _write_graph_matrix_format(G, output_file) else: raise RuntimeError( "[Internal error] Format {} not implemented".format(file_format)) # # In-house parsers # def _kthlist_parse(inputfile): """Read a graph from file, and produce the datas. First yeild (#vertex,first comment line) Then generates a sequence of (s,target,lineno) Raises: ValueError is parsing fails for some reason """ # vertex number size = -1 name = "" for i, l in enumerate(inputfile.readlines()): # first non empty comment line is the graph name # must be before the graph size if l[0] == 'c': if size < 0 and len(name) == 0 and len(l[2:].strip()) != 0: name += l[2:] continue # empty line if len(l.strip()) == 0: continue if ':' not in l: # vertex number spec if size >= 0: raise ValueError( "Line {} contains a second spec directive.".format(i)) try: size = int(l.strip()) if size < 0: raise ValueError except ValueError: raise ValueError( "Non negative number expected at line {}.".format(i)) yield (size, name) continue # Load edges from this line left, right = l.split(':') try: left = int(left.strip()) right = [int(s) for s in right.split()] except ValueError: raise ValueError("Non integer vertex ID at line {}.".format(i)) if len(right) < 1 or right[-1] != 0: raise ValueError("Line {} must end with 0.".format(i)) if left < 1 or left > size: raise ValueError( "Vertex ID out of range [1,{}] at line {}.".format(size, i)) right.pop() if len([x for x in right if x < 1 or x > size]) > 0: raise ValueError( "Vertex ID out of range [1,{}] at line {}.".format(size, i)) yield left, right, i def _read_bipartite_kthlist(inputfile): """Read a bipartite graph from file, in the KTH reverse adjacency lists format. Assumes the adjacecy list is given in order. - vertices are listed in increasing order - if bipartite, only the adjiacency list of the left side must be given, no list for a vertex of the right side is allowed. Parameters ---------- inputfile : file object file handle of the input Raises ------ ValueError Error parsing the file """ # vertex number parser = _kthlist_parse(inputfile) size, name = next(parser) bipartition_ambiguous = [1, size] edges = {} previous = 0 for left, right, lineno in parser: if left <= previous: raise ValueError( "Vertex at line {} is smaller than the previous one.".format(lineno)) # Check the bi-coloring on both side if left > bipartition_ambiguous[1]: raise ValueError( "Bipartition violation al line {}. Vertex {} cannot be on the left side." .format(lineno, left)) bipartition_ambiguous[0] = max(bipartition_ambiguous[0], left + 1) for v in right: if v < bipartition_ambiguous[0]: raise ValueError( "Bipartition violation. Invalid edge ({},{}) at line {}." .format(left, v, lineno)) bipartition_ambiguous[1] = min(bipartition_ambiguous[1], v - 1) # after vertices, add the edges edges[left] = right # fix the bipartition # unsassigned vertices go to the right size L = bipartition_ambiguous[0]-1 R = size - bipartition_ambiguous[0]+1 G = BipartiteGraph(L, R, name) for u in edges: for v in edges[u]: G.add_edge(u, v - L) if size != G.number_of_vertices(): raise ValueError("{} vertices expected. Got {} instead.".format( size, G.number_of_vertices())) return G def _read_nonbipartite_kthlist(inputfile, graph_class): """Read a graph from file, in the KTH reverse adjacency lists format. Only for simple and directed graph Assumes the adjacecy list is given in order. - vertices are listed in increasing order - if directed graph the adjacency list specifies incoming neighbous - if DAG, the graph must be given in topological order source->sink Parameters ---------- inputfile : file object file handle of the input graph_class: class either Graph or DirectedGraph Raises ------ ValueError Error parsing the file """ assert graph_class in [Graph, DirectedGraph] # vertex number parser = _kthlist_parse(inputfile) size, name = next(parser) G = graph_class(size, name) previous = 0 for succ, predecessors, lineno in parser: if succ <= previous: raise ValueError( "Vertex at line {} is smaller than the previous one.".format(lineno)) # after vertices, add the edges for v in predecessors: G.add_edge(v, succ) previous = succ if size != G.order(): raise ValueError("{} vertices expected. Got {} instead.".format( size, G.order())) return G def _read_graph_dimacs_format(inputfile, graph_class): """Read a graph simple from file, in the DIMACS edge format. Parameters ---------- inputfile : file object file handle of the input graph_class: class object either Graph or DirectedGraph """ assert graph_class in [Graph, DirectedGraph] G = None name = '' n = -1 m = -1 m_cnt = 0 # is the input topologically sorted? for i, l in enumerate(inputfile.readlines()): l = l.strip() # add the comment to the header if l[0] == 'c': name += l[2:] continue # parse spec line if l[0] == 'p': if G is not None: raise ValueError( "[Syntax error] " + "Line {} contains a second spec line.".format(i+1)) _, fmt, nstr, mstr = l.split() if fmt != 'edge': raise ValueError("[Input error] " + "Dimacs \'edge\' format expected at line {}.".format(i+1)) n = int(nstr) m = int(mstr) G = graph_class(n, name) continue # parse spec line if l[0] == 'e': if G is None: raise ValueError("[Input error] " + "Edge before preamble at line".format(i)) m_cnt += 1 _, v, w = l.split() try: G.add_edge(int(v), int(w)) except ValueError: raise ValueError("[Syntax error] " + "Line {} syntax error: edge must be 'e u v' where u, v are vertices".format(i)) if m != m_cnt: raise ValueError("[Syntax error] " + "{} edges were expected.".format(m)) return G def _read_graph_matrix_format(inputfile): """Read a bipartite graph from file, in the adjiacency matrix format. This is an example of an adjacency matrix for a bipartite graph with 9 vertices on one side and 15 on the another side. .. 9 15 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 0 0 0 0 0 0 0 1 1 0 1 0 0 0 Parameters ---------- inputfile: file object the file containing the graph specification Returns ------- G : BipartiteGraph """ def scan_integer(inputfile): num_buffer = [] line_cnt = 0 while True: if len(num_buffer) == 0: line = inputfile.readline() if len(line) == 0: return line_cnt += 1 tokens = line.split() if len(tokens) == 0 or tokens[0][0] == '#': continue # comment line try: num_buffer.extend((int(lit), line_cnt) for lit in tokens) except ValueError: raise ValueError("[Syntax error] " + "Line {} contains a non numeric entry.". format(line_cnt)) yield num_buffer.pop(0) scanner = scan_integer(inputfile) try: n = next(scanner)[0] m = next(scanner)[0] G = BipartiteGraph(n, m) G.name = '' # read edges for i in range(1, n + 1): for j in range(1, m + 1): (b, l) = next(scanner) if b == 1: G.add_edge(i, j) elif b == 0: pass else: raise ValueError( "[Input error at line {}] Only 0 or 1 are allowed". format(l)) except StopIteration: raise ValueError("[Input error] Unexpected end of the matrix") # check that there are is no more data try: (b, l) = next(scanner) raise ValueError( "[Input error at line {}] There are more than {}x{} entries". format(l, n, m)) except StopIteration: pass return G # # In-house graph writers # def _write_graph_kthlist_nonbipartite(G, output_file): """Wrire a graph to a file, in the KTH reverse adjacency lists format. Parameters ---------- G : Graph or DirectGraph the graph to write on file output_file : file object file handle of the output """ assert isinstance(G, (Graph, DirectedGraph)) print("c {}".format(G.name), file=output_file) print("{}".format(G.order()), file=output_file) from io import StringIO output = StringIO() for v in G.vertices(): if G.is_directed(): nbors = G.predecessors(v) else: nbors = G.neighbors(v) output.write(str(v) + " :") output.write("".join([' '+str(i) for i in nbors])) output.write(" 0\n") print(output.getvalue(), file=output_file) def _write_graph_kthlist_bipartite(G, output_file): """Wrire a bipartite graph to a file, in the KTH reverse adjacency lists format. Parameters ---------- G : BipartiteGraph the graph to write on file output_file : file object file handle of the output """ assert isinstance(G, BipartiteGraph) print("c {}".format(G.name), file=output_file) print("{}".format(G.order()), file=output_file) from io import StringIO output = StringIO() U, _ = G.parts() offset = len(U) for u in U: output.write(str(u) + " :") output.write("".join([' '+str(v + offset) for v in G.right_neighbors(u)])) output.write(" 0\n") print(output.getvalue(), file=output_file) def _write_graph_dimacs_format(G, output_file): """Wrire a graph to a file, in DIMACS format. Parameters ---------- G : Graph or DirectGraph the graph to write on file output_file : file object file handle of the output """ assert isinstance(G, (Graph, DirectedGraph)) print("c {}".format(G.name).strip(), file=output_file) n = G.number_of_vertices() m = G.number_of_edges() print("p edge {} {}".format(n, m), file=output_file) for v, w in G.edges(): print("e {} {}".format(v, w), file=output_file) def _write_graph_matrix_format(G, output_file): """Wrire a graph to a file, in \"matrix\" format. Parameters ---------- G : BipartiteGraph the graph to write in output output_file : file object file handle of the output """ assert isinstance(G, BipartiteGraph) print("{} {}".format(G.left_order(), G.right_order()), file=output_file) L, R = G.parts() for u in L: adj_row = [] for v in R: if G.has_edge(u, v): adj_row.append("1") else: adj_row.append("0") print(" ".join(adj_row), file=output_file) # # Bipartite graph generator # (we do not want to use networkx) # def bipartite_random_left_regular(l, r, d, seed=None): """Returns a random bipartite graph with constant left degree. Each vertex on the left side has `d` neighbors on the right side, picked uniformly at random without repetition. Each vertex in the graph has an attribute `bipartite` which is 0 for the vertices on the left side and 1 for the vertices on the right side. Parameters ---------- l : int vertices on the left side r : int vertices on the right side d : int degree on the left side. seed : hashable object seed the random generator Returns ------- BipartiteGraph Raises ------ ValueError unless ``l``, ``r`` and ``d`` are non negative. """ import random if seed is not None: random.seed(seed) if l < 0 or r < 0 or d < 0: raise ValueError( "bipartite_random_left_regular(l,r,d) needs l,r,d >=0.") G = BipartiteGraph(l, r) G.name = "bipartite_random_left_regular({},{},{})".format(l, r, d) d = min(r, d) L, R = G.parts() for u in L: for v in sorted(random.sample(R, d)): G.add_edge(u, v) return G def bipartite_random_m_edges(L, R, m, seed=None): """Returns a random bipartite graph with M edges Build a random bipartite graph with :math:`L` left vertices, :math:`R` right vertices and :math:`m` edges sampled at random without repetition. Parameters ---------- L : int vertices on the left side R : int vertices on the right side m : int number of edges. seed : hashable object seed the random generator Returns ------- BipartiteGraph Raises ------ ValueError unless ``L``, ``R`` and ``m`` are non negative. """ import random if seed is not None: random.seed(seed) if L < 1 or R < 1 or m < 0 or m > L * R: raise ValueError( "bipartite_random_m_edges(L,R,m) needs L, R >= 1, 0<=m<=L*R") G = BipartiteGraph(L, R) G.name = "bipartite_random_m_edges({},{},{})".format(L, R, m) U, V = G.parts() if m > L * R // 3: # Sampling strategy (dense) E = ((u, v) for u in U for v in V) for u, v in random.sample(E, m): G.add_edge(u, v) else: # Sampling strategy (sparse) count = 0 while count < m: u = random.randint(1, L) v = random.randint(1, R) if not G.has_edge(u, v): G.add_edge(u, v) count += 1 assert G.number_of_edges() == m return G def bipartite_random(L, R, p, seed=None): """Returns a random bipartite graph with independent edges Build a random bipartite graph with :math:`L` left vertices, :math:`R` right vertices, where each edge is sampled independently with probability :math:`p`. Parameters ---------- L : int vertices on the left side R : int vertices on the right side p : float probability to pick an edge seed : hashable object seed the random generator Returns ------- BipartiteGraph Raises ------ ValueError unless ``L``, ``R`` are non negative and 0<=``p``<=1. """ import random if seed is not None: random.seed(seed) if L < 1 or R < 1 or p < 0 or p > 1: raise ValueError( "bipartite_random_graph(L,R,p) needs L, R >= 1, p in [0,1]") G = BipartiteGraph(L, R) G.name = "bipartite_random_graph({},{},{})".format(L, R, p) U, V = G.parts() for u in U: for v in V: if random.random() <= p: G.add_edge(u, v) return G def bipartite_shift(N, M, pattern=[]): """Returns a bipartite graph where edges are a fixed shifted sequence. The graph has :math:`N` vertices on the left (numbered from :math:`1` to :math:`N`), and :math:`M` vertices on the right (numbered from :math:`1` to :math:`M`), Each vertex :math:`v` on the left side has edges to vertices :math:`v+d_1`, :math:`v+d_2`, :math:`v+d_3`,... with vertex indices on the right wrap around :wrap around over :math:`[1..M]`). Notice that this construction does not produces multiedges even if two offsets end up on the same right vertex. Parameters ---------- N : int vertices on the left side M : int vertices on the right side pattern : list(int) pattern of neighbors Returns ------- BipartiteGraph Raises ------ ValueError unless ``N``, ``M`` are non negative and ``pattern`` has vertices outside the range. """ if N < 1 or M < 1: raise ValueError("bipartite_shift(N,M,pattern) needs N,M >= 0.") G = BipartiteGraph(N, M) G.name = "bipartite_shift_regular({},{},{})".format(N, M, pattern) L, R = G.parts() pattern.sort() for u in L: for offset in pattern: G.add_edge(u, 1 + (u - 1 + offset) % M) return G def bipartite_random_regular(l, r, d, seed=None): """Returns a random bipartite graph with constant degree on both sides. The graph is d-regular on the left side and regular on the right size, so it must be that d*l / r is an integer number. Parameters ---------- l : int vertices on the left side r : int vertices on the right side d : int degree of vertices at the left side seed : hashable object seed of random generator Returns ------- BipartiteGraph Raises ------ ValueError if one among ``l``, ``r`` and ``d`` is negative or if ``r`` does not divides `l*d` References ---------- [1] http://... """ import random if seed is not None: random.seed(seed) if l < 0 or r < 0 or d < 0: raise ValueError("bipartite_random_regular(l,r,d) needs l,r,d >=0.") if (l * d) % r != 0: raise ValueError( "bipartite_random_regular(l,r,d) needs r to divid l*d.") G = BipartiteGraph(l, r) G.name = "bipartite_random_regular({},{},{})".format(l, r, d) L, R = G.parts() A = list(L) * d B = list(R) * (l * d // r) assert len(B) == l * d for i in range(l * d): # Sample an edge, do not add it if it existed # We expect to sample at most d^2 edges for retries in range(3 * d * d): ea = random.randint(i, l * d - 1) eb = random.randint(i, l * d - 1) if not G.has_edge(A[ea], B[eb]): G.add_edge(A[ea], B[eb]) A[i], A[ea] = A[ea], A[i] B[i], B[eb] = B[eb], B[i] break else: # Sampling takes too long, maybe no good edge exists failure = True for ea in range(i, l * d): for eb in range(i, l * d): if not G.has_edge(A[ea], B[eb]): failure = False break if not failure: break if failure: return bipartite_random_regular(l, r, d) return G def dag_pyramid(height): """Generates the pyramid DAG Vertices are indexed from the bottom layer, starting from index 1 Parameters ---------- height : int the height of the pyramid graph (>=0) Returns ------- cnfgen.graphs.DirectedGraph Raises ------ ValueError """ if height < 0: raise ValueError("The height of the tree must be >= 0") n = (height+1)*(height+2) // 2 # number of vertices D = DirectedGraph(n, 'Pyramid of height {}'.format(height)) # edges leftsrc = 1 dest = height+2 for layer in range(1, height+1): for i in range(1, height-layer+2): D.add_edge(leftsrc, dest) D.add_edge(leftsrc+1, dest) leftsrc += 1 dest += 1 leftsrc += 1 return D def dag_complete_binary_tree(height): """Generates the complete binary tree DAG Vertices are indexed from the bottom layer, starting from index 1 Parameters ---------- height : int the height of the tree Returns ------- cnfgen.graphs.DirectedGraph Raises ------ ValueError """ if height < 0: raise ValueError("The height of the tree must be >= 0") # vertices plus 1 N = 2 * (2**height) name = 'Complete binary tree of height {}'.format(height) D = DirectedGraph(N-1, name) # edges leftsrc = 1 for dest in range(N // 2 + 1, N): D.add_edge(leftsrc, dest) D.add_edge(leftsrc+1, dest) leftsrc += 2 return D def dag_path(length): """Generates a directed path DAG Vertices are indexed from 1..length+1 Parameters ---------- length : int the length of the path Returns ------- cnfgen.graphs.DirectedGraph Raises ------ ValueError """ if length < 0: raise ValueError("The lenght of the path must be >= 0") name = 'Directed path of length {}'.format(length) D = DirectedGraph(length+1, name) # edges for i in range(1, length+1): D.add_edge(i, i + 1) return D def split_random_edges(G,k, seed=None): """Split m random missing edges to G If :math:`G` is a simple graph, it picks k random edges (and fails if there are not enough of them), and splits the edges in 2 adding a new vertex for each of them. Parameters ---------- G : Graph a graph with at least :math:`m` missing edges k : int the number of edges to sample seed : hashable object seed of random generator Example ------- >>> G = Graph(5) >>> G.add_edges_from([(1,4),(4,5),(2,4),(2,3)]) >>> G.number_of_edges() 4 >>> split_random_edges(G,2) >>> G.number_of_edges() 6 >>> G.number_of_vertices() 7 """ if seed is not None: random.seed(seed) if not isinstance(G,Graph): raise TypeError("Edge splitting is only implemented for simple graphs") non_negative_int(k,'k') if k > G.number_of_edges(): raise ValueError("The graph does not have {} edges.".format(k)) tosplit = random.sample(list(G.edges()),k) nv = G.number_of_vertices() G.update_vertex_number(nv+k) x = nv + 1 for u,v in tosplit: G.remove_edge(u,v) G.add_edge(u,x) G.add_edge(x,v) x += 1 def add_random_missing_edges(G, m, seed=None): """Add m random missing edges to G If :math:`G` is not complete and has at least :math:`m` missing edges, :math:`m` of them are sampled and added to the graph. Parameters ---------- G : Graph a graph with at least :math:`m` missing edges m : int the number of missing edges to sample seed : hashable object seed of random generator Raises ------ ValueError if :math:`G` doesn't have :math:`m` missing edges RuntimeError Sampling failure in the sparse case """ if seed is not None: random.seed(seed) if m < 0: raise ValueError("You can only sample a non negative number of edges.") total_number_of_edges = None if G.is_bipartite(): Left, Right = G.parts() total_number_of_edges = len(Left) * len(Right) def edge_sampler(): u = random.sample(Left, 1)[0] v = random.sample(Right, 1)[0] return (u, v) def available_edges(): return [(u, v) for u in Left for v in Right if not G.has_edge(u, v)] else: V = G.number_of_vertices() total_number_of_edges = V * (V - 1) / 2 def edge_sampler(): return random.sample(range(1, V+1), 2) def available_edges(): result = [] for u in range(1, V): for v in range(u+1, V+1): if not G.has_edge(u, v): result.append((u, v)) return result # How many edges we want in the end? goal = G.number_of_edges() + m if goal > total_number_of_edges: raise ValueError( "The graph does not have {} missing edges to sample.".format(m)) # Sparse case: sample and retry for _ in range(10 * m): if G.number_of_edges() >= goal: break u, v = edge_sampler() if not G.has_edge(u, v): G.add_edge(u, v) if G.number_of_edges() < goal: # Very unlikely case: sampling process failed and the solution # is to use the sampling process tailored for denser graph, so # that a correct result is guaranteed. This requires # generating all available edges for u, v in random.sample(available_edges(), goal - G.number_of_edges()): G.add_edge(u, v) def supported_graph_formats(): """File formats supported for graph I/O Given as a dictionary that maps graph types to the respective supported formats. E.g. 'dag' -> ['dimacs', 'kthlist'] """ return {'simple': Graph.supported_file_formats(), 'digraph': DirectedGraph.supported_file_formats(), 'dag': DirectedGraph.supported_file_formats(), 'bipartite': BipartiteGraph.supported_file_formats()}   localtypes.py #!/usr/bin/env python # -*- coding:utf-8 -*- """Functions to check the arguments types """ import numbers def positive_int(value, name): """Check that `value` is a positive integer""" msg = "argument '{}' must be a positive integer".format(name) if not isinstance(value, numbers.Integral): raise TypeError(msg) if value < 1: raise ValueError(msg) def positive_int_seq(value, name): """Check that `value` is a positive integer""" msg = "argument '{}' must be a sequence of positive integers".format(name) try: for v in value: if not isinstance(v, numbers.Integral): raise TypeError('non numeric element in the sequence') except TypeError as te: raise TypeError(msg) from te for v in value: if v < 1: raise ValueError(msg) def non_negative_int_seq(value, name): """Check that `value` is a positive integer""" msg = "argument '{}' must be a sequence of non negative integers".format(name) try: for v in value: if not isinstance(v, numbers.Integral): raise TypeError('non numeric element in the sequence') except TypeError as te: raise TypeError(msg) from te for v in value: if v < 0: raise ValueError(msg) def one_of_values(value, name, choices): '''Check if the value is in a specific set''' msg = "argument '{}' must be one of [{}]".format(name, choices) if value not in choices: raise ValueError(msg) def any_int(value, name): """Check that `value` is an integer""" msg = "argument '{}' must be have integer value".format(name) if not isinstance(value, numbers.Integral): raise TypeError(msg) def non_negative_int(value, name): """Check that the `value` is a non negative""" msg = "argument '{}' must be a non negative integer".format(name) if not isinstance(value, numbers.Integral): raise TypeError(msg) if value < 0: raise ValueError(msg) def probability_value(value, name): """Check that the `value` is a real between 0 and 1""" msg = "argument '{}' must be a real between 0 and 1".format(name) if not isinstance(value, numbers.Real): raise TypeError(msg) if value < 0 or value > 1: raise ValueError(msg)   2.1 Generating hard instances Considering the outline of methods used in current DPLL-based SAT-solvers we can now make an observation about graphs which should lead to hard instances EC(G). First let us restrict our attention to graphs G which are obtained by picking an edge in a 4-regular graph on n vertices and subdividing it, i.e. introducing a new vertex as midpoint of the old edge. For such a graph EC(G) will be unsatisfiable, have 2n + 1 variables and 10n + 2 clauses. This gives us unsatisfiable formulae with a density of close to 5 clauses per variable. For formulae with clauses of length 4 this is a density for which a formula from the random 4-SAT ensemble is expected to be satisfiable, see e.g. [1]. In this random model a formula is constructed by for each possible clause of length 4, for a set of n variables, letting it be part of the formula with probability p. Random 4-SAT formulae with expected density 5 are also expected to be easy to solve. 考虑到目前基于dpll的sat求解器所使用的方法的大纲，我们现在可以对图进行观察，这将导致硬实例EC(G)。 首先让我们将注意力限制在图G上，图G是通过在n个顶点上的4正则图中选取一条边并将其细分而得到的，即引入一个新顶点作为旧边的中点。 对于这样一个EC(G)将不能满足的图，有2n + 1个变量和10n + 2子句。这给了我们无法满足的公式，每个变量的密度接近5个子句。对于子句长度为4的公式，这是一个密度4-SAT集合预期可以满足。 在这个随机模型中，对于n个变量集，每个长度为4的可能子句，构造一个公式，让它成为公式的一部分，概率为p。期望密度为5的随机4-SAT公式也很容易求解。   What can we say about the smallest number of variables involved in a nontrivial conflict, allowing us to learn a new clause, in a formula of this kind? We can get a simple lower bound for this by observing that we must at least set all variables corresponding to the edges of some cycle C in G before a nontrivial conflict can arise. Getting more accurate lower bounds is harder, but this tells us that the girth of the graph can be used to control the size of conflict sets. 在一个非微不足道的冲突中，我们可以用最小的变量数量来学习一个新的子句，在这种公式中，我们能说什么呢? 我们可以得到一个简单的下界，通过观察，我们必须至少设置对应于G中某个循环C的边的所有变量，才能产生非平凡的冲突。 获得更精确的下界是比较困难的，但这告诉我们，图的周长可以用来控制冲突集的大小。   This immediately draws our attention to 4-regular graphs, keeping the clause length low, of high girth. If the girth of G is g we will at first not be able to learn any nontrivial clauses of length less than, at least, g. If the SAT-solver we are using has a cut–off length for the clauses it learns, i.e. it does no retain any conflict clauses with more than some number k of literals, it will in fact be prevented from learning any new clauses at all, thus reducing it to a pure DPLL procedure. 这立即将我们的注意力吸引到4规则图上，保持子句长度低，周长高。如果G的周长是G，我们首先将无法学习任何长度至少小于G的非平凡子句。如果我们正在使用的sat -求解器对它学习的子句有一个截断长度，即它不保留任何冲突子句，其字面量不超过k个，那么它实际上将无法学习任何新的子句，从而将其简化为一个纯粹的DPLL过程。   If the solver uses restarts and removes long clauses when it performs a restart it will in a similar way risk changing into a DPLL procedure with learning, but with an effective run time corresponding to the time between consecutive restarts. 如果求解器在执行重新启动时使用重新启动并删除长子句，那么它将以类似的方式冒着变成具有学习功能的DPLL过程的风险，但其有效运行时间对应于连续重新启动之间的时间间隔。   With this in mind it seems natural to use formulae of the form EC(G) based on 4-regular graphs, as described, as challenging unsatisfiable instances for SAT-solvers. If the formulae are to be tuned for hardness then using graphs with high girth, or at least few short cycles, also seems natural. If hard solvable instances are desired one could apply the methods of [14] on EC(G). The paper [14] presents a construction which, based on a hard unsatisfiable formula builds a solvable formula which is hard for a broad class of solvers. 考虑到这一点，使用基于4正则图的EC(G)形式的公式似乎是很自然的，正如所描述的，作为sat求解者的不满意的挑战实例。如果要调整公式的硬度，那么使用高周长的图，或者至少有几个短周期的图，似乎也很自然。如果需要难解的实例，可以采用的方法 在EC (G)[14]。论文[14]给出了一个构造，它在一个难解不满足公式的基础上，建立了一个对广义求解器来说难解的可解公式。
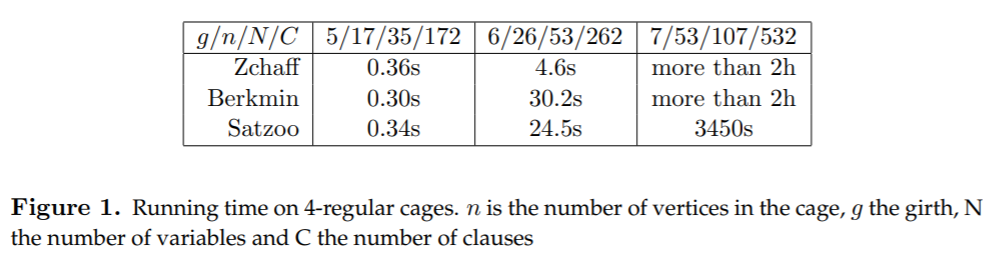
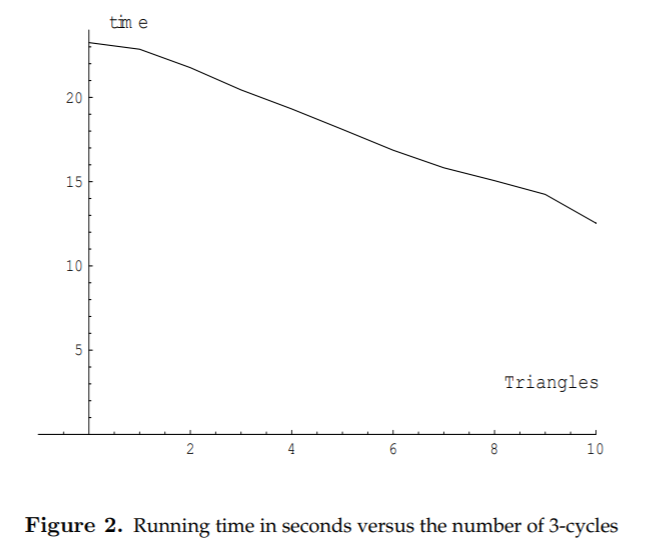
	3. Experiments
	4. Conclusions and further directions Both our discussion in 2.1 and the experiments in the previous section clearly indicate the importance of small dense structures, such as triangles in the Eulerian graphs, for the hardness of an instance of the type considered here. However we would expect this to be true in greater generality. Let us make this a bit more precise. Given a k-SAT formula F let us look at its clause-variable incidence graph, i.e., the graph with one vertex for each variable, one vertex for each clause, and an edge between a variable-vertex and a clause-vertex if the variable is present in the clause. Given a subset S of the variables we define F[S], the induced subformula of F on S, to be the set of clauses C in F such that C only contains variables present in S. The density of the formula F[S] is as usual the number of clauses in F[S] divided by |S|. If a formula F has many dense subformulae a clause learning DPLL-solver has a good chance of learning new short conflict clauses due to conflicts within a dense local part. However for a given clause length k there exist a density r(k) such that a formula with clauses of length at most k and density less than r(k) is always satisfiable. So, if an unsatisfiable formula F lacks such local dense parts a solver will initially have to assign values to many variables in order to find a conflict and learn a new clause. In this case the learnt clauses will also tend to be quite long. If we look at random k-SAT instances of fixed clause to variable density we will only expect a small number of short cycles in the clause-variable incidence graph, actually an asymptotically size independent number, just as in the case of random regular graphs [3]. As a consequence, the density of F[S] will typically be very small, often less than 1, for variables sets S of small size. Likewise our formulae EC(G) will lack small dense subformulae when the underlying graph G has high girth. If we instead use random regular graphs G we know, [3], that there will typically exist only a small number of cycles in G and no small subgraphs denser than a cycle. In this case the formulae EC(G) will thereby inherit expected properties much like those for random k-SAT. Thus some of the experimentally observed hardness of random unsatisfiable instances may well come from their lack of local dense subformulae. Here an experimental study of running times for unsolvable random instances versus the number of short cycles in their incidence graphs could be interesting. In this context, it is interesting to note that for satisfiable instances this lack of local dense parts is considered to be responsible for some of the success of randomized algorithms like the survey propagation method [4]. An interesting possibility would be to make more explicit use of the structure of the clause-variable incidence graph of an instance in resolution methods as well. This could e.g. be used to control the choice of resolution variable in the DPLL procedure. In order to reduced the risk of the kind of trap the EC(G)-formulae represent for clause learning SAT-solvers some simple modifications can be added. One addition which seems cost effective would be to keep track of a running mean of the size of the clauses discovered during the learning process and keep all clauses not much larger than the current mean. That way long clauses would still be kept for formulae in which no short clauses are possible to learn without first learning long clauses. However, the general problem faced here is still the fundamental limitations of solvers which do not use a proof system stronger than general resolution. While producing more optimised resolution based solvers is undoubtedly a worthwhile undertaking it is becoming more and more important to find efficient algorithms based on stronger proof systems.   References [1] Dimitris Achlioptas and Yuval Peres. The threshold for random k-SAT is 2 k log 2−O(k). J. Amer. Math. Soc., 17(4):947–973 (electronic), 2004. [2] Paul Beame, Henry Kautz, and Ashish Sabharwal. Towards understanding and harnessing the potential of clause learning. J. Artificial Intelligence Res., 22:319–351 (electronic), 2004. [3] B´ela Bollob´as. Random graphs, volume 73 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, second edition, 2001. [4] A. Braunstein, M. M´ezard, and R. Zecchina. Survey propagation: an algorithm for satisfiability. Random Structures Algorithms, 27(2):201–226, 2005. [5] Martin Davis, George Logemann, and Donald Loveland. A machine program for theorem-proving. Comm. ACM, 5:394–397, 1962. [6] Martin Davis and Hilary Putnam. A computing procedure for quantification theory. J. Assoc. Comput. Mach., 7:201–215, 1960. [7] Nicklas Een and Niklas S¨orensson. Webpage for satzoo and minisat at chalmers university. http://www.cs.chalmers.se/∼een/Satzoo/. [8] Nicklas Een and Niklas S¨orensson. An extensible sat-solver. In Lecture Notes in Computer Science, 2919,SAT 2003, pages 502–518, 2004. [9] Eugene Goldberg and Yakov Novikov. Webpage for berkmin. http://heigold.tripod.com/BerkMin.html. [10] Edward A. Hirsch and Arist Kojevnikov. UnitWalk: a new SAT solver that uses local search guided by unit clause elimination. Ann. Math. Artif. Intell., 43(1-4):91–111, 2005. Theory and applications of satisfiability testing. [11] Hans Kleine Buning ¨ and Theodor Lettman. Propositional logic: deduction and algorithms, volume 48 of Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge, 1999. Translated from the 1994 German original by the authors. [12] Anton Kotzig. Moves without forbidden transitions in a graph. Mat. Casopis ˇ Sloven. Akad. Vied, 18:76–80, 1968. [13] Klas Markstr¨om. Web page of current author, see combinatorial data and programs. http://www.math.umu.se/∼klasm. [14] Edward A. Hirsch Michael Alekhnovich and Dmitry Itsykson. Exponential lower bounds for the running time of DPLL algorithms on satisfiable formulas. In International Colloquium on Automata, Languages and Programming,ICALP 2004, pages 84–96, 2004. [15] R´emi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman, and Lidror Troyansky. Determining computational complexity from characteristic “phase transitions”. Nature, 400(6740):133–137, 1999. [16] Gordon Royle. Gordon royles homepages for combinatorial data. http://www.cs.uwa.edu.au/∼gordon/remote/cubics/index.html. [17] Alasdair Urquhart. Hard examples for resolution. J. Assoc. Comput. Mach., 34(1):209– 219, 1987. [18] Douglas B. West. Introduction to graph theory. Prentice Hall Inc., Upper Saddle River, NJ, 1996. [19] Lintao Zhang. webpage for zchaff at princeton university. http://www.princeton.edu/∼chaff/zchaff.html. [20] Lintao Zhang, Conor F. Madigan, Matthew W. Moskewicz, and Sharad Malik. Efficient conflict driven learning in boolean satisfiability solver. In International Conference on Computer Aided Design, ICCAD 2001, pages 279–285, 2001.