Proofs for Satisfiability Problems
Marijn J.H. Heule and Armin Biere
1 The University of Texas at Austin, United States
2 Johannes Kepler University, Linz, Austria
Unsatisfiability proofs are useful for several applications, such as computing interpolants and MUS extraction. These proofs can also be used to validate results of the SAT solvers that produced them and for tools that use SAT solvers, such as theorem provers.不可满足性证明在插值计算和MUS提取等方面具有重要的应用价值。这些证明也可以用来验证产生它们的SAT求解器的结果,以及使用SAT求解器的工具,如定理证明器.
1 Introduction
|
Satisfiability (SAT) solvers have become powerful tools to solve a wide range of applications. In case SAT problems are satisfiable, it is easy to validate a witness. However, if SAT problems have no solutions, a proof of unsatisfiability is required to validate that result. Apart from validation, proofs of unsatisfiability are useful in several applications, such as interpolation [64] and extracting a minimal unsatisfiable set (MUS[49] and in tools that use SAT solvers such as theorem provers [4,65,66,67]. 译文:然而,如果SAT问题没有解,则需要用不满足证明来验证该结果。
Since the beginning of validating the results of SAT solvers, proof logging of unsatisfiability claims was based on two approaches: resolution proofs and clausal proofs. Resolution proofs, discussed in zChaff in 2003 [69], require for learned clauses (lemmas) a list of antecedents. On the other hand, for clausal proofs, as described in Berkmin in 2003 [32], the proof checker needs to find the antecedents for lemmas. Consequently, resolution proofs are much larger than clausal proofs, while resolution proofs are easier and faster to validate than clausal proofs 译文:自SAT解算结果验证开始以来,不可满足索赔的证明日志建立在两种方法上:解析证明和条款证明。 译文:2003年zChaff[69]讨论了决议证明,要求学习子句(引理)具有先行词列表。 译文:另一方面,对于子句证明,如Berkmin在2003[32]中所描述的,证明检查器需要找到引理的前例。 译文:因此,分解证明比分句证明大得多,而分解证明比分句证明更容易、更快地验证。
Both proof approaches are used in different settings. Resolution proofs are often required in applications like interpolation [47] or in advanced techniques for MUS extraction [50]. Clausal proofs are more popular in the context of validating results of SAT solvers, for example during the SAT Competitions or recently for the proof of Erd˝os Discrepancy Theorem [41]. Recent works also use clausal proofs for interpolation [33] and MUS extraction [11].
Proof logging support became widespread in state-of-the-art solvers, such as Lingeling [13], Glucose [7], and CryptoMiniSAT [57], since SAT Competition 2013 made unsatisfiability proofs mandatory for solvers participating in the unsatisfiability tracks. About half the solvers that participated in recent SAT Competitions can emit clausal proofs, including the strongest solvers around, for example the three solvers mentioned above. However, very few solvers support emitting resolution proofs. 译文:因为2013年SAT竞赛对参与不满足轨道的求解者强制要求不满足证明。
The lack of support for resolution proofs is due to the difficulty to represent some techniques used in contemporary SAT solvers in terms of resolution. One such technique is conflict clause minimization [58], which requires several modifications of the solver in order to express it using resolution steps [62]. In contrast, emitting a clausal proof from SAT solvers such as MiniSAT [28] and Glucose requires only small changes to the code3 . 译文:相反,从SAT求解器(如MiniSAT[28]和Glucose)发出子句证明只需要对代码3进行小的更改。
|
|
2 Proof Systems
|
A proof of unsatisfiability shows why the unsatisfiable empty clause is redundant (i.e., its addition preserves satisfiability) with respect to a given CNF formula. 译文:一个不能满足的证明表明,对于给定的CNF公式,为什么不能满足的空子句是多余的(即,它的添加保持了可满足性)。
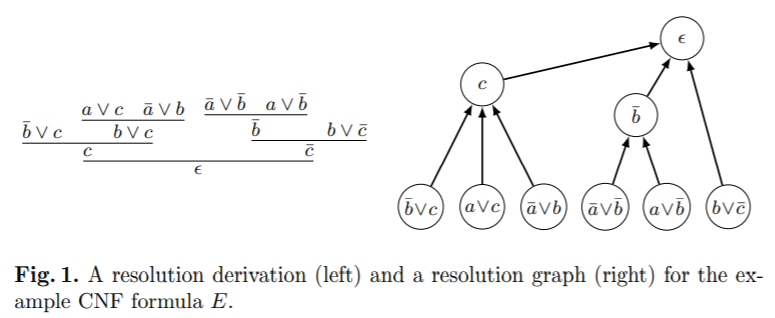
译文:归结链是一个归结操作的序列,最后一个操作的结果是下一个操作的前提。
译文:与推导CDCL解算器中的子句相比,传统的程序以相反的顺序应用单位传播来显示公式中隐含的这些习得的子句。
译文:关于证明系统的两个重要概括是阻塞子句添加[42]和决议不对称子句添加[40]。
|
|
3 Proof Search
|
The leading paradigm to solve satisfiability problems is the conflict-driven clause learning (CDCL) approach [46]. In short, CDCL adds lemmas, typically referred to as conflict clauses, to a given input formula until either it finds a satisfying assignment or is able to learn (i.e., deduce) the empty clause (prove unsatisfiability). We refer to a survey on the CDCL paradigm for details [46]. 译文:简而言之,CDCL向给定的输入公式添加引理,通常称为冲突子句,直到它找到满意的赋值或能够学习(即推导)空子句(证明不满足性)。我们参考一份关于CDCL范式的调查来了解细节[46]。
An alternative approach to solve satisfiability problems is the lookahead approach [38]. Lookahead solvers solve a problem via a binary search-tree. In each node of the search-tree, the best splitting variable is selected using so-called lookahead techniques. Although it is possible to extract unsatisfiability proofs from lookahead solvers, it hardly happens in practice and hence we ignore lookahead solvers in the remainder of this chapter.
CDCL solvers typically use a range of preprocessing techniques, such as bounded variable elimination (also known as Davis-Putnam resolution) [25,26], blocked clause elimination [39], subsumption, and hyper binary resolution [8]. Preprocessing techniques are frequently crucial to solve large formulas efficiently. These preprocessing can also be used during the solving phase, which is known as inprocessing [40]. Most preprocessing techniques can be expressed using a few resolutions, such as bounded variable elimination and hyper binary resolution. Other techniques can be ignored in the context of unsatisfiability proofs, because they weaken the formula, such as blocked clause elimination and subsumption. A few techniques can only be expressed in extended resolution or its generalizations, such as bounded variable addition [45] and blocked clause addition [40]. 译文:CDCL求解器通常使用一系列预处理技术,如有界变量消除(也称为Davis-Putnam分辨率)[25,26],阻塞子句消除[39],包容和超二进制分辨率[8]。
Some CDCL solvers use preprocessing techniques which are hard to represent using existing proof formats. Examples of such techniques are Gaussian Elimination (GE), Cardinality Resolution (CR) [23] and Symmetry Breaking (SB) [1]. These techniques cannot be polynomially simulated using resolution: Certain formulas based on expander graphs are hard for resolution [60], i.e., resolution proofs are exponentially large, while GE can solve them efficiently. Similarly, formulas arising from the pigeon hole principle are hard for resolution [34], but they can be solved efficiently using either CR or SB. Consequently, resolution proofs of solvers that use these techniques may be exponentially large in the size of the solving time. At the moment, there is no solver that produces resolution proofs for these techniques. 译文:一些CDCL求解器使用预处理技术,这很难用现有的证明格式来表示。 译文:这些技术不能用分辨率多项式地模拟:基于展开器图的某些公式对于分辨率[60]来说是困难的,即分辨率证明是指数级大的,而GE可以高效地求解。 译文:因此,使用这些技术的求解器的分辨率证明在求解时间的大小上可能是指数级大的。目前,还没有一个求解器可以为这些技术生成分辨率证明。
Techniques such as GE, CR, and SB, can be simulated polynomially using extended resolution and its generalizations. However, it is not know how to simulate these techniques efficiently / elegantly using extended resolution. One method to translate GE into extended resolution proofs is to convert the GE steps into BDDs and afterwards translate the BDDs to extended resolution [55]. 译文:利用扩展分辨率及其推广,可以多项式地模拟GE、CR和SB等技术。然而,它不知道如何使用扩展分辨率高效/优雅地模拟这些技术。 |
|
4 Proof Formats
|
4.2 Clausal Proofs We appeal to the notion that lemmas are used to construct a proof of a theorem. Here, lemmas represent the learned clauses and the theorem is the statement that the formula is unsatisfiable. From now on, we will use the term clauses to refer to input clauses, while lemmas will refer to added clauses.
The DRUP (delete reverse unit propagation) format [36] extends RUP by integrating clause deletion information into proofs. The main reason to add clause deletion information to a proof is to reduce the cost to validate a proof which will be discussed in Section 6.2. Clause deletion information is expressed using the prefix d.
4.3 Proofs with Extended Resolution So far we only considered proof formats that validate techniques that can be simulated using resolution. Some SAT solver use techniques that cannot be simulated using resolution, such as blocked clause addition [42]. To validate these techniques, proof formats need to support a richer representation that includes extended resolution or one of its generalizations. 译文:为了验证这些技术,证明格式需要支持更丰富的表示,包括扩展解析或其泛化之一。 译文:分辨率证明,顾名思义,只能用于检查基于分辨率的技术。TraceCheck格式部分支持扩展解析,因为可以使用一个空的先决条件列表从扩展规则中添加子句。因此,这些子句被认为是输入子句,而没有实际验证它们。 译文:RUP和RAT格式之间的区别在于冗余检查,它是在该格式的证明检查器中计算出来的。
译文:每行以子句标识符(粗体)开始,然后包含原始子句或引理的字面量,最后以子句标识符列表(粗体)结束。
|
|
8 Conclusions
|
Unsatisfiability proofs are useful for several applications, such as computing interpolants and MUS extraction. These proofs can also be used to validate results of the SAT solvers that produced them and for tools that use SAT solvers, such as theorem provers. There are two types of unsatisfiability proofs: resolution proofs and clausal proofs. Resolution proofs are used for most applications, but they are hard to produce. Therefore very few SAT solvers support resolution proof logging. Clausal proof logging is easy and therefore most state-of-the-art solvers support it. However, validating clausal proofs is costly, although recent advances significantly improved performance of checkers. There are several challenges regarding unsatisfiability proofs. How can one store resolution proofs using much less space on disk and using much less memory overhead? Can the costs of validating clausal proofs be further be reduced? Last but not least, research is required to study how some techniques, such as Gaussian elimination, cardinality resolution, and symmetry breaking, can be expressed elegantly in unsatisfiability proofs. |
|
References
|
1. Fadi A. Aloul, Karem A. Sakallah, and Igor L. Markov. Efficient symmetry breaking for Boolean satisfiability. IEEE Trans. Computers, 55(5):549–558, 2006. 2. Hasan Amjad. Compressing propositional refutations. Electr. Notes Theor. Comput. Sci., 185:3–15, 2007. 3. Zaher S. Andraus, Mark H. Liffiton, and Karem A. Sakallah. Refinement strategies for verification methods based on datapath abstraction. In Proc. ASP-DAC’06, pages 19–24. IEEE, 2006. 4. Micha¨el Armand, Germain Faure, Benjamin Gr´egoire, Chantal Keller, Laurent Th´ery, and Benjamin Werner. Verifying SAT and SMT in Coq for a fully automated decision procedure. In International Workshop on Proof-Search in Axiomatic Theories and Type Theories (PSATTT), 2011. 5. Cyrille Artho, Armin Biere, and Martina Seidl. Model-based testing for verification back-ends. In Margus Veanes and Luca Vigan`o, editors, TAP, volume 7942 of Lecture Notes in Computer Science, pages 39–55. Springer, 2013. 6. Roberto As´ın, Robert Nieuwenhuis, Albert Oliveras, and Enric Rodr´ıguezCarbonell. Efficient generation of unsatisfiability proofs and cores in SAT. In Iliano Cervesato, Helmut Veith, and Andrei Voronkov, editors, LPAR, volume 5330 of Lecture Notes in Computer Science, pages 16–30. Springer, 2008. 7. Gilles Audemard and Laurent Simon. Glucose 2.3 in the SAT 2013 Competition. In Anton Belov, Marijn J. H. Heule, and Matti J¨arvisalo, editors, Proceedings of SAT Competition 2013, volume B-2013-1 of Department of Computer Science Series of Publications B, University of Helsinki, pages 42–43, 2013. 8. Fahiem Bacchus and Jonathan Winter. Effective preprocessing with hyperresolution and equality reduction. In Giunchiglia and Tacchella [30], pages 341–355. 9. Omer Bar-Ilan, Oded Fuhrmann, Shlomo Hoory, Ohad Shacham, and Ofer Strichman. Linear-time reductions of resolution proofs. In Hana Chockler and Alan J. Hu, editors, Haifa Verification Conference, volume 5394 of Lecture Notes in Computer Science, pages 114–128. Springer, 2008. 10. Paul Beame, Henry Kautz, and Ashish Sabharwal. Towards understanding and harnessing the potential of clause learning. JAIR, 22:319–351, 2004. 11. Anton Belov, Marijn J. H. Heule, and Joao P. Marques-Silva. Mus extraction using clausal proofs. In Carsten Sinz and Uwe Egly, editors, Theory and Applications of Satisfiability Testing SAT 2014, volume 8561 of Lecture Notes in Computer Science, pages 48–57. Springer International Publishing, 2014. 12. Armin Biere. PicoSAT essentials. Journal on Satisfiability, Boolean Modeling and Computation (JSAT), 4:75–97, 2008. 13. Armin Biere. Lingeling, Plingeling and Treengeling entering the SAT Competition 2013. In Anton Belov, Marijn J. H. Heule, and Matti J¨arvisalo, editors, Proceedings of SAT Competition 2013, volume B-2013-1 of Department of Computer Science Series of Publications B, University of Helsinki, pages 51–52, 2013. 14. Armin Biere. Yet another local search solver and Lingeling and friends entering the SAT Competition 2014. In Anton Belov, Marijn J. H. Heule, and Matti J¨arvisalo, editors, SAT Competition 2014, volume B-2014-2 of Department of Computer Science Series of Publications B, pages 39–40. University of Helsinki, 2014. 15. Roderick Bloem and Natasha Sharygina, editors. Proceedings of 10th International Conference on Formal Methods in Computer-Aided Design, FMCAD 2010, Lugano, Switzerland, October 20-23. IEEE, 2010. 16. Joseph Boudou, Andreas Fellner, and Bruno Woltzenlogel Paleo. Skeptik: A proof compression system. In St´ephane Demri, Deepak Kapur, and Christoph Weidenbach, editors, Automated Reasoning - 7th International Joint Conference, IJCAR 2014, Held as Part of the Vienna Summer of Logic, VSL 2014, Vienna, Austria, July 19-22, 2014. Proceedings, volume 8562 of Lecture Notes in Computer Science, pages 374–380. Springer, 2014. 17. Aaron R. Bradley. SAT-based model checking without unrolling. In Ranjit Jhala and David A. Schmidt, editors, VMCAI, volume 6538 of Lecture Notes in Computer Science, pages 70–87. Springer, 2011. 18. Robert Brummayer and Armin Biere. Effective bit-width and underapproximation. In Proc. EUROCAST’09, volume 5717 of LNCS, pages 304–311, 2009. 19. Robert Brummayer and Armin Biere. Fuzzing and delta-debugging SMT solvers. In International Workshop on Satisfiability Modulo Theories (SMT), pages 1–5. ACM, 2009. 20. Robert Brummayer, Florian Lonsing, and Armin Biere. Automated testing and debugging of SAT and QBF solvers. In Theory and Applications of Satisfiability Testing (SAT), volume 6175 of LNCS, pages 44–57. Springer, 2010. 21. Stephen A. Cook. The complexity of theorem-proving procedures. In Proceedings of the Third Annual ACM Symposium on Theory of Computing, STOC ’71, pages 151–158, New York, NY, USA, 1971. ACM. 22. Stephen A. Cook and Robert A. Reckhow. The relative efficiency of propositional proof systems. The Journal of Symbolic Logic, 44(1):pp. 36–50, 1979. 23. W. Cook, C.R. Coullard, and Gy. Tur´an. On the complexity of cutting-plane proofs. Discrete Applied Mathematics, 18(1):25 – 38, 1987. 24. Scott Cotton. Two techniques for minimizing resolution proofs. In Ofer Strichman and Stefan Szeider, editors, Theory and Applications of Satisfiability Testing SAT 2010, volume 6175 of Lecture Notes in Computer Science, pages 306–312. Springer, 2010. 25. Martin Davis and Hilary Putnam. A computing procedure for quantification theory. J. ACM, 7(3):201–215, 1960. 26. Niklas E´en and Armin Biere. Effective preprocessing in SAT through variable and clause elimination. In Fahiem Bacchus and Toby Walsh, editors, SAT, volume 3569 of Lecture Notes in Computer Science, pages 61–75. Springer, 2005. 27. Niklas E´en, Alan Mishchenko, and Nina Amla. A single-instance incremental SAT formulation of proof- and counterexample-based abstraction. In Bloem and Sharygina [15], pages 181–188. 28. Niklas E´en and Niklas S¨orensson. An extensible SAT-solver. In Giunchiglia and Tacchella [30], pages 502–518. 29. Pascal Fontaine, Stephan Merz, and Bruno Woltzenlogel Paleo. Compression of propositional resolution proofs via partial regularization. In Nikolaj Bjørner and Viorica Sofronie-Stokkermans, editors, Automated Deduction - CADE-23 - 23rd International Conference on Automated Deduction, Wroclaw, Poland, July 31 - August 5, 2011. Proceedings, volume 6803 of Lecture Notes in Computer Science, pages 237–251. Springer, 2011. 30. Enrico Giunchiglia and Armando Tacchella, editors. Theory and Applications of Satisfiability Testing, 6th International Conference, SAT 2003. Santa Margherita Ligure, Italy, May 5-8, 2003 Selected Revised Papers, volume 2919 of Lecture Notes in Computer Science. Springer, 2004. 31. Andreas Goerdt. Comparing the complexity of regular and unrestricted resolution. In Heinz Marburger, editor, GWAI-90 14th German Workshop on Artificial Intelligence, volume 251 of Informatik-Fachberichte, pages 181–185. Springer Berlin Heidelberg, 1990. 32. Evguenii I. Goldberg and Yakov Novikov. Verification of proofs of unsatisfiability for CNF formulas. In Design, Automation and Test in Europe Conference and Exhibition (DATE), pages 10886–10891. IEEE, 2003. 33. Arie Gurfinkel and Yakir Vizel. Druping for interpolants. In Proceedings of the 14th Conference on Formal Methods in Computer-Aided Design, FMCAD ’14, pages 19:99–19:106, Austin, TX, 2014. FMCAD Inc. 34. Armin Haken. The intractability of resolution. Theor. Comput. Sci., 39:297–308, 1985. 35. HyoJung Han and Fabio Somenzi. On-the-fly clause improvement. In Kullmann [43], pages 209–222. 36. Marijn J. H. Heule, Warren A. Hunt, Jr., and Nathan Wetzler. Trimming while checking clausal proofs. In Formal Methods in Computer-Aided Design (FMCAD), pages 181–188. IEEE, 2013. 37. Marijn J. H. Heule, Warren A. Hunt, Jr., and Nathan Wetzler. Verifying refutations with extended resolution. In International Conference on Automated Deduction (CADE), volume 7898 of LNAI, pages 345–359. Springer, 2013. 38. Marijn J. H. Heule and Hans van Maaren. Handbook of Satisfiability, volume 185 of Frontiers in Artificial Intelligence and Applications, chapter Chapter 5, LookAhead Based SAT Solvers, pages 155–184. IOS Press, February 2009. 39. Matti J¨arvisalo, Armin Biere, and Marijn Heule. Simulating circuit-level simplifications on CNF. J. Autom. Reasoning, 49(4):583–619, 2012. 40. Matti J¨arvisalo, Marijn J. H. Heule, and Armin Biere. Inprocessing rules. In International Joint Conference on Automated Reasoning (IJCAR), volume 7364 of LNCS, pages 355–370. Springer, 2012. 41. Boris Konev and Alexei Lisitsa. A SAT attack on the erdos discrepancy conjecture. 2014. Accepted for SAT 2014. 42. Oliver Kullmann. On a generalization of extended resolution. Discrete Applied Mathematics, 96-97:149–176, 1999. 43. Oliver Kullmann, editor. Theory and Applications of Satisfiability Testing - SAT 2009, 12th International Conference, SAT 2009, Swansea, UK, June 30 - July 3, 2009. Proceedings, volume 5584 of Lecture Notes in Computer Science. Springer, 2009. 44. Jean-Marie Lagniez and Armin Biere. Factoring out assumptions to speed up MUS extraction. In Matti J¨arvisalo and Allen Van Gelder, editors, SAT, volume 7962 of Lecture Notes in Computer Science, pages 276–292. Springer, 2013. 45. Norbert Manthey, Marijn J. H. Heule, and Armin Biere. Automated reencoding of Boolean formulas. In Proceedings of Haifa Verification Conference (HVC), volume 6397 of LNCS, pages 102–117. Springer, 2012. 46. Joao P. Marques-Silva, Ines Lynce, and Sharad Malik. Handbook of Satisfiability, volume 185 of Frontiers in Artificial Intelligence and Applications, chapter Chapter 4, Conflict-Driven Clause Learning SAT Solvers, pages 131–153. IOS Press, February 2009. 47. Kenneth L. McMillan. Interpolation and SAT-based model checking. In Warren A. Hunt Jr. and Fabio Somenzi, editors, CAV, volume 2725 of Lecture Notes in Computer Science, pages 1–13. Springer, 2003. 48. Ant´onio Morgado, Federico Heras, Mark H. Liffiton, Jordi Planes, and Joao Marques-Silva. Iterative and core-guided MaxSAT solving: A survey and assessment. Constraints, 18(4):478–534, 2013. 49. Alexander Nadel. Boosting minimal unsatisfiable core extraction. In Bloem and Sharygina [15], pages 221–229. 50. Alexander Nadel, Vadim Ryvchin, and Ofer Strichman. Efficient MUS extraction with resolution. In FMCAD, pages 197–200. IEEE, 2013. 51. Alexander N¨ohrer, Armin Biere, and Alexander Egyed. Managing SAT inconsistencies with HUMUS. In Proc. VaMoS’12, pages 83–91. ACM, 2012. 52. J. A. Robinson. A machine-oriented logic based on the resolution principle. J. ACM, 12(1):23–41, January 1965. 53. Simone Fulvio Rollini, Roberto Bruttomesso, Natasha Sharygina, and Aliaksei Tsitovich. Resolution proof transformation for compression and interpolation. Formal Methods in System Design, 45(1):1–41, 2014. 54. Carsten Sinz. Compressing propositional proofs by common subproof extraction. In Roberto Moreno-D´ıaz, Franz Pichler, and Alexis Quesada-Arencibia, editors, EUROCAST, volume 4739 of Lecture Notes in Computer Science, pages 547–555. Springer, 2007. 55. Carsten Sinz and Armin Biere. Extended resolution proofs for conjoining bdds. In Dima Grigoriev, John Harrison, and Edward A. Hirsch, editors, CSR, volume 3967 of Lecture Notes in Computer Science, pages 600–611. Springer, 2006. 56. Carsten Sinz, Andreas Kaiser, and Wolfgang K¨uchlin. Formal methods for the validation of automotive product configuration data. Artif. Intell. Eng. Des. Anal. Manuf., 17(1):75–97, January 2003. 57. Mate Soos. Strangenight. In A. Belov, M. Heule, and M. J¨arvisalo, editors, Proceedings of SAT Competition 2013, volume B-2013-1 of Department of Computer Science Series of Publications B, University of Helsinki, pages 89–90, 2013. 58. Niklas S¨orensson and Armin Biere. Minimizing learned clauses. In Kullmann [43], pages 237–243. 59. Grigori S. Tseitin. On the complexity of derivation in propositional calculus. In Automation of Reasoning 2, pages 466–483. Springer, 1983. 60. Alasdair Urquhart. Hard examples for resolution. J. ACM, 34(1):209–219, 1987. 61. Allen Van Gelder. Verifying RUP proofs of propositional unsatisfiability. In International Symposium on Artificial Intelligence and Mathematics (ISAIM), 2008. 62. Allen Van Gelder. Improved conflict-clause minimization leads to improved propositional proof traces. In Kullmann [43], pages 141–146. 63. Allen Van Gelder. Producing and verifying extremely large propositional refutations - have your cake and eat it too. Ann. Math. Artif. Intell., 65(4):329–372, 2012. 64. Yakir Vizel, Vadim Ryvchin, and Alexander Nadel. Efficient generation of small interpolants in CNF. In Natasha Sharygina and Helmut Veith, editors, CAV, volume 8044 of Lecture Notes in Computer Science, pages 330–346. Springer, 2013. 65. Tjark Weber. Efficiently checking propositional resolution proofs in Isabelle/HOL. In International Workshop on the Implementation of Logics (IWIL), volume 212, pages 44–62, 2006. 66. Tjark Weber and Hasan Amjad. Efficiently checking propositional refutations in HOL theorem provers. Journal of Applied Logic, 7(1):26–40, 2009. 67. Nathan Wetzler, Marijn J. H. Heule, and Warren A. Hunt, Jr. Mechanical verification of SAT refutations with extended resolution. In Conference on Interactive Theorem Proving (ITP), volume 7998 of LNCS, pages 229–244. Springer, 2013. 68. Nathan Wetzler, Marijn J. H. Heule, and Warren A. Hunt, Jr. DRAT-trim: Efficient checking and trimming using expressive clausal proofs. In Theory and Applications of Satisfiability Testing (SAT), 2014. 69. Lintao Zhang and Sharad Malik. Validating SAT solvers using an independent resolution-based checker: Practical implementations and other applications. In Proceedings of the conference on Design, Automation and Test in Europe - Volume 1, DATE ’03, pages 10880–10885. IEEE Computer Society, 2003. |
|