core-tier2-local三个集合管理子句的文献:An Experimental Study of Permanently Stored Learned Clauses
文献1:2019,较新
Exploiting Glue Clauses to Design Effective CDCL Branching Heuristics
| Abstract |
In conflict-directed clause learning (CDCL) SAT solving, a In this work, we relate glue clauses to decision variables. First, we show experimentally that branching decisions with variables appearing in glue clauses, called glue variables, are more conflict efficient than with nonglue variables. 在这项工作中,我们把粘合子句与决策变量联系起来。首先,我们通过实验证明,带有出现在glue子句中的变量(称为glue变量)的分支决策比带有非语言变量的分支决策更具冲突效率。 This observation motivated the development of a structure-aware CDCL variable bumping scheme, which increases the heuristic score of a glue variable based on its appearance count in the glue clauses that are learned so far by the search.这一观察结果推动了一种结构感知的CDCL变量碰撞方案的发展,该方案根据一个glue变量在搜索到目前为止所学习到的glue子句中的出现计数来增加glue变量的启发式得分。 Empirical evaluation shows the effectiveness of the Finally, we show that the frequency of learned clauses that are glue clauses can be used as a reliable indicator of solving efficiency for some instances, for which the standard performance metrics fail to provide a consistent explanation. 最后,我们表明,对于一些标准性能指标无法提供一致的解释的情况,学习的子句(即粘合子句)的频率可以作为解决效率的可靠指标。 |
文献2:2019,较为细致 introduce a simple online clause reduction scheme
Simplifying CDCL Clause Database Reduction
Jamali, S., Mitchell, D. (2019). Simplifying CDCL Clause Database Reduction. In: Janota, M., Lynce, I. (eds)
Theory and Applications of Satisfiability Testing – SAT 2019. SAT 2019. Lecture Notes in Computer Science(),
vol 11628. Springer, Cham. https://doi.org/10.1007/978-3-030-24258-9_12
| Abstract | CDCL SAT solvers generate many “learned” clauses, so effective clause database reduction strategies are important to performance. Over time reduction strategies have become complex, increasing the difficulty of evaluating particular factors or introducing new refinements. At the same time, it has been unclear if the complexity is necessary. We introduce a simple online clause reduction scheme, which involves no sorting. We instantiate this scheme with simple mechanisms for taking into account clause activity and LBD within the winning solver from the 2018 SAT Solver Competition, obtaining performance comparable to the original. We also present empirical data on the effects of simple measures of clause age, activity and LBD on performance. |
| online clause reduction scheme |
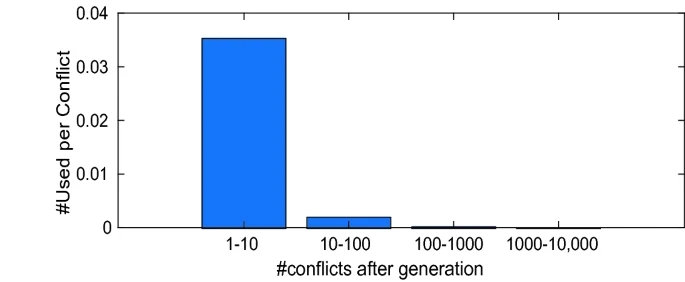
circular list L 循环链表 When a new learned clause C needs to be stored in Local, we select a “low quality” clause in the list to be replaced with C by sequential search.
Relating Delete-Half and Online Deletion. dynamically estimating the median ------ q Age-Based Deletion. Each new learned clause replaces the oldest clause in Local. This very low-cost scheme works surprisingly well. 这个非常低成本的方案效果出奇的好。
|
|
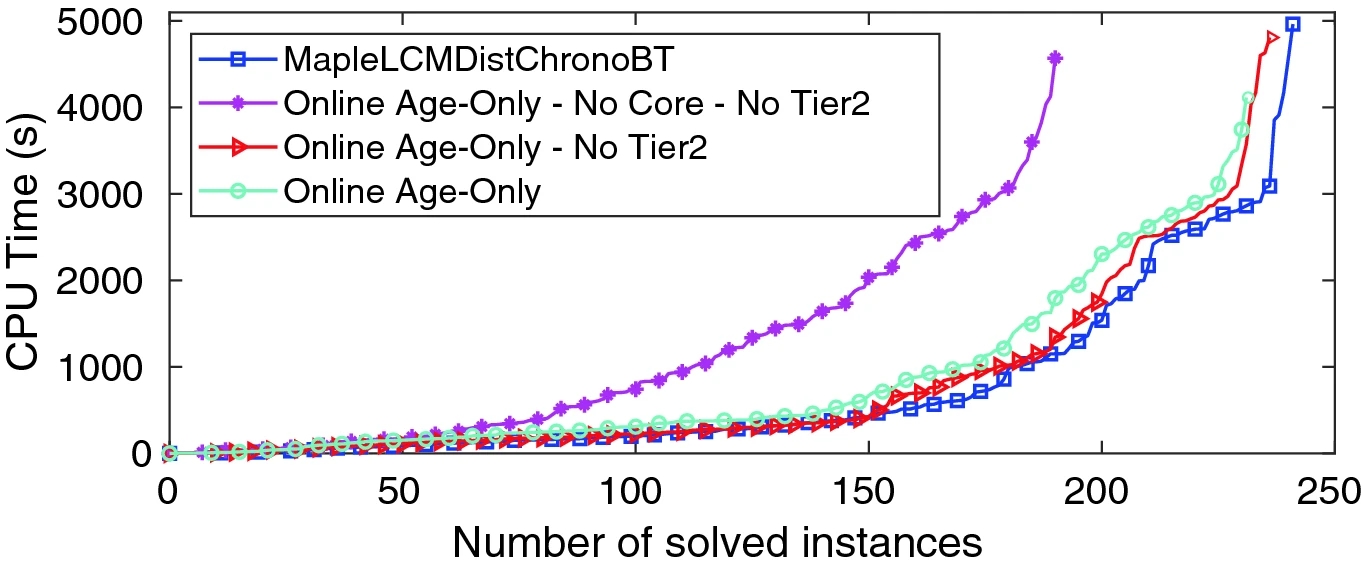
图形解读基本结论1:
Core and Tier2 are important to the performance of MapleLCMDistChronoBT. It also shows that in the presence of Core and Tier2 a simple pure age-based deletion scheme for Local gives quite good performance.它还表明,在Core和Tier2存在的情况下,一个简单的纯基于年龄的本地删除方案具有相当好的性能.
图形解读基本结论2:
age is highly correlated with usage rate, and can account for a large fraction of decisions that would be made based on clause activities.年龄与使用率高度相关,可以在基于子句活动的决策中占很大一部分。
RU ------ Recently-Used
|
|
| 4 clause lbd and tier2 |
将子句的lbd值与子句最近使用次数挂钩; 将local进入iter2的子句予以保留; |
| 5 discussion |
We introduced a new, simple online clause deletion scheme, and reported the performance of instantiations of the scheme using clause age, LBD and very simple measures of usage. An implementation of the online scheme in MapleLCMDistChronoBT, the winning solver from the main track of the 2018 SAT Solver Competition, has performance almost as good as the original.
Online deletion requires less computation time than the Delete-Half scheme. However, the fraction of run time consumed by deletion in MapleLCMDistChronoBT is small, so this is not a major performance factor. 在线删除比删除-一半方案需要更少的计算时间。然而,在MapleLCMDistChronoBT中删除所消耗的运行时间的比例很小,所以这不是一个主要的性能因素。 The online deletion schemes in this paper use age or age modified by a fixed quality threshold. A dynamic threshold may be more desirable, in which case we may use a feedback control scheme to ensure the threshold is such that the fraction of saved clauses is suitable. We continue to investigate more refined versions of our scheme, in particular with regard to clause quality measures and clause database size. Table 2 shows that our modified solvers are biased toward Satisfiable instances, and we will work on shifting this bias. |
Coverage-Based Clause Reduction Heuristics for CDCL Solvers
Nabeshima, H., Inoue, K. (2017). Coverage-Based Clause Reduction Heuristics for CDCL Solvers. In: Gaspers, S., Walsh, T. (eds) Theory and Applications of Satisfiability Testing – SAT 2017. SAT 2017. Lecture Notes in Computer Science(), vol 10491. Springer, Cham. https://doi.org/10.1007/978-3-319-66263-3_9
| abstract |
Many heuristics, such as decision, restart, and clause reduction heuristics, are incorporated in CDCL solvers in order to improve performance. In this paper, we focus on learnt clause reduction heuristics, which are used to suppress memory consumption and sustain propagation speed. The reduction heuristics consist of evaluation criteria, for measuring the usefulness of learnt clauses, and a reduction strategy in order to select clauses to be removed based on the criteria. LBD (literals blocks distance) is used as the evaluation criteria in many solvers. 约简启发式算法包括衡量学习过的句子有用性的评价标准,以及根据这些标准选择要删除的句子的约简策略。在许多求解器中,LBD(文字块距离)被用作评价标准。 For the reduction strategy, we propose a new concise schema based on the coverage ratio of used LBDs. 我们提出了一种基于已用lbd覆盖率的简洁模式. The experimental results show that the proposed strategy can achieve higher coverage than the conventional strategy and improve the performance for both SAT and UNSAT instances. |
| 1 intraduction |
In this paper, we present experimental evidence of the identification power of LBD in a wide range of instances. 在本文中,我们提出了LBD在广泛的实例中识别能力的实验证据。 Moreover, we show that an appropriate threshold for LBD, which are used to decide if clauses should be maintained or not, is determined depending on a given instance. 根据给定的实例确定LBD的适当阈值,用于决定是否应该维护子句。 However, a certain fixed threshold of LBD is often used in latter reduction strategies. In this paper, we propose a new reduction strategy based on the coverage of used LBDs, which dynamically computes an appropriate LBD threshold in order to cover most propagations and conflicts. 本文提出了一种新的基于LBD覆盖范围的减少策略,该策略动态计算出一个合适的LBD阈值,以覆盖大部分传播和冲突。 The experimental results show that our schema effectively maintains the used clauses and achieves performance improvement for both SAT and UNSAT instances. |
| 2 Clause Reduction Heuristics |
base policy ------ BP two exceptional conditions ------- EP 两个异常情况
Half of learnt clauses are removed in descending order of LBD except the following clauses.
This Glucose reduction strategy and its derivatives are used in many solvers. For example, Lingeling dynamically selects either Glucose-based or classical activity-based strategies [4]. If the standard deviation of the LBDs of learnt clauses is too small or too large, then, the activity-based strategy is selected. MapleCOMSPS uses the reduction strategy combining both. This keeps clauses whose LBDs <span class="MathJax_Preview"><span id="MathJax-Element-8-Frame" class="MathJax" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>≤</mo><mn>6</mn></math>"><span id="MathJax-Span-80" class="math"><span id="MathJax-Span-81" class="mrow"><span id="MathJax-Span-82" class="mo">≤<span id="MathJax-Span-83" class="mn">6≤6, while others are managed by the activity-based strategy. <span class="MathJax_Preview"><span id="MathJax-Element-8-Frame" class="MathJax" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>≤</mo><mn>6</mn></math>"><span class="MJX_Assistive_MathML">In addition, clauses with LBDs of 4 to 6, which have not been used for a while, are managed by the activity-based strategy [<a id="ref-link-section-d32859403e1151" title="Oh, C.: Between SAT and UNSAT: the fundamental difference in CDCL SAT. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 307–323. Springer, Cham (2015). doi: 10.1007/978-3-319-24318-4_23 " href="https://link.springer.com/chapter/10.1007/978-3-319-66263-3_9#ref-CR8" data-track="click" data-track-action="reference anchor" data-track-label="link" data-test="citation-ref">8</a>].
<span class="MathJax_Preview"><span id="MathJax-Element-8-Frame" class="MathJax" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><mo>≤</mo><mn>6</mn></math>"><span class="MJX_Assistive_MathML">In Sect. <a href="https://link.springer.com/chapter/10.1007/978-3-319-66263-3_9#Sec4" data-track="click" data-track-label="link" data-track-action="section anchor">4</a>, we show some issues in the <span class="u-sans-serif">Glucose reduction strategy. |
| 3 Experimental Evaluation of LBD |
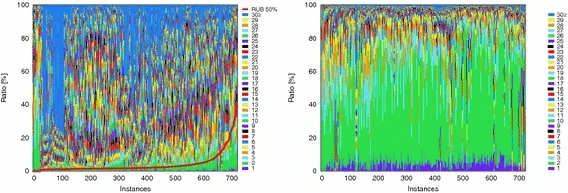
Figure 1 shows the distributions of LBDs of learnt clauses (left) and used LBDs (right) for each instance. 图1显示了每个实例中学习子句的lbd分布(左)和使用子句的lbd分布(右)。 In this experiment, learnt clause reduction was disabled; that is, the solver held every learnt clause. 在本实验中,习得的从句减少被禁用;也就是说,解算器掌握了每一个已学会的子句。
The numbers in the legend represent LBDs. The red line in the left graph will be explained in Sect. 4. Each stacked bar in the left graph represents the ratio distribution of LBDs, for all learnt clauses, after the solver stopped (e.g., if there are 10% learnt clauses whose LBDs are 2, the height of LBD 2 bar is 10%). In the right graph, each bar represents the ratio distribution of clause LBDs, which caused propagations or conflicts (e.g., if 50% of propagations or conflicts are caused by LBD 2 clauses, then the height of the LBD 2 bar is 50%). 图例中的数字表示lbd。左图中的红线将在第4节中解释。(The red line in the left graph of Fig. 1 represents the upper bound of the number of clauses held when following BP. 图1左图中的红线表示跟随BP时所保持的子句数量的上界。如果删除策略被使用,就不会有这么多的子句被展示出来了) 左侧图中每个堆叠的条形图表示解算器停止后,所有已学习子句的lbd的比例分布; 在右边的图中,每个条形图表示子句lbd的比例分布,导致传播或冲突;
The left graph shows that learnt clauses have various LBDs. In easy instances at the left end of the graph, small LBDs are somewhat dominant;在图左端的简单例子中,小lbd在一定程度上占主导地位; however, the other instances have many different LBDs. On the other hand, from the right graph, it is clear that most propagations or conflicts are caused by small LBD clauses. 大多数传播或冲突是由小LBD子句引起的。 This strongly supports the identification power of the LBD criterion.
|
| 4 Issues of Glucose Reduction Strategy |
(1) On the other hand, the interval between reductions increases exponentially. This means that the ratio of number of clauses that can be newly held, gradually approaches 0 as k increases. This is the first issue regarding BP. 随着k的增加,可以新持有的子句数量的比例逐渐接近0。这是关于BP的第一个问题。 在大多数情况下,glue子句的数量超过了界限。 因此,只要解算器遵循BP和E1,解算器就完全不能保留新的无胶子句。
(2) 此外,仅保留glue子句(E1)有时不足以涵盖大多数传播和冲突。 在图1的右图中,底部的紫色和绿色条表示LBD 1和2的比例。这表明LBD的合适上界取决于给定的实例。这是关于E1的第二个问题。
(3)过度驻留一些不断更新的子句 In Glucose, clauses used after the last reduction and with LBD less than, or equal to 30, are not removed (E2). The right graph in Fig. 1 shows that this threshold can cover most propagations and conflicts; however, it may be overly retentive. This is the third issue related to E2.
在下一节中,我们将提出一种新的简明的减少策略来解决上述问题。 |
| 5 Coverage-Based Reduction Strategy |
Most propagations and conflicts are caused by small LBD clauses. We propose a reduction strategy to dynamically compute the upper bound of LBD in order to cover most propagations and conflicts.大多数传播和冲突是由小LBD子句引起的。为了覆盖大部分的传播和冲突,我们提出了一种动态计算LBD上界的缩减策略。
In order to suppress the number of held clauses while covering propagations and conflicts as much as possible, we classify learnt clauses into three types: core, support, and other clauses.
基于已使用lbd的频率分布。 |
| 6 Experimental Results |
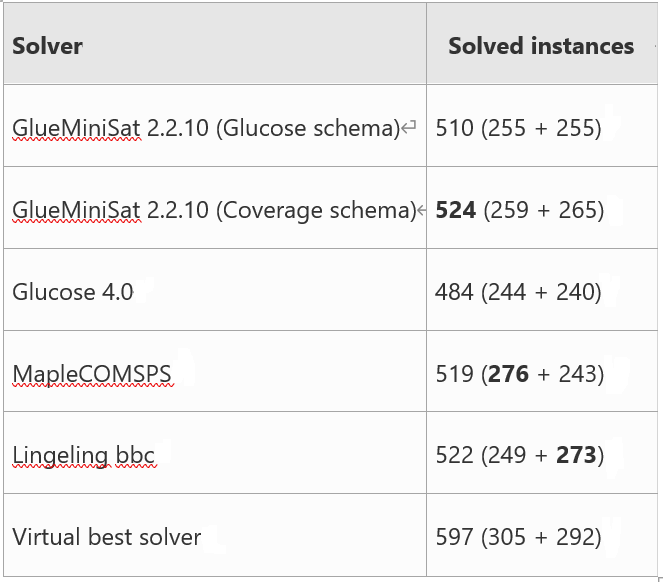
Table 1. Solved instances, where “X (Y + Z)” denotes the number of solved instances (X), solved satisfiable instances (Y) and solved unsatisfiable instances (Z), respectively.
Table 1 shows the number of instances solved by each solver and Fig. 3 is the cactus plot of these results. GlueMiniSat, with the Glucose schema, has better performance than Glucose. The coverage schema can further improve performance for both SAT and UNSAT instances. MapleCOMSPS and Lingeling show the superior results for SAT and UNSAT instances, respectively. GlueMiniSat, with the coverage schema, shows that the well-balanced result and total number of solved instances are comparable with these state of the art solvers. GlueMiniSat,与覆盖模式,显示了良好平衡的结果和解决的实例总数可以与这些先进的求解器相媲美。
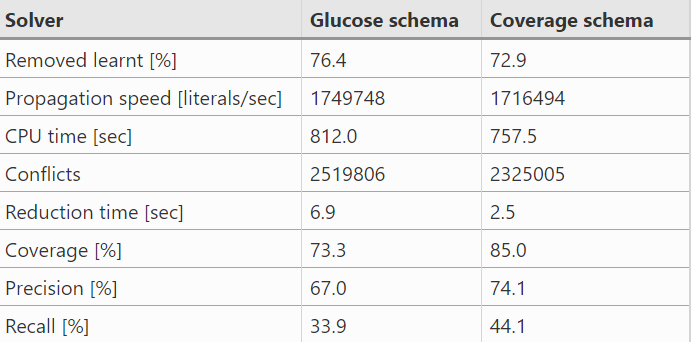
Table 2. Comparison of two reduction strategies in GlueMiniSat.
Table 2 is the comparison of statistics between Glucose and coverage schema. Each value in the first 5 lines denotes the average for commonly solved 494 instances of both strategies. 前两行 The first two lines in the table show that the Glucose schema reduces more clauses than the coverage schema; hence, the Glucose schema shows higher propagation speed. 第三第四行第五行 On the other hand, the coverage schema requires shorter CPU time and less conflicts in order to solve instances. It shows that the coverage schema can hold more useful clauses than the Glucose schema. In the coverage schema, the reduction of learnt clauses is slightly faster since the computational cost is O(n) while the Glucose schema is <span class="MathJax_Preview"><span id="MathJax-Element-56-Frame" class="MathJax" data-mathml="&lt;math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot;&gt;&lt;mi&gt;O&lt;/mi&gt;&lt;mo stretchy=&quot;false&quot;&gt;(&lt;/mo&gt;&lt;mi&gt;n&lt;/mi&gt;&lt;mi&gt;log&lt;/mi&gt;&lt;mo&gt;&amp;#x2061;&lt;/mo&gt;&lt;mi&gt;n&lt;/mi&gt;&lt;mo stretchy=&quot;false&quot;&gt;)&lt;/mo&gt;&lt;/math&gt;"><span id="MathJax-Span-873" class="math"><span id="MathJax-Span-874" class="mrow"><span id="MathJax-Span-875" class="mi">O<span id="MathJax-Span-876" class="mo">(<span id="MathJax-Span-877" class="mi">n<span id="MathJax-Span-878" class="mi">log<span id="MathJax-Span-879" class="mo"><span id="MathJax-Span-880" class="mi">n<span id="MathJax-Span-881" class="mo">)O(nlogn).
最后三行 The last three lines in Table 2 are the results of different experiments, in which each solver does not actually remove learnt clauses to calculate coverage, precision, and recall. Each value indicates the average for commonly solved 406 instances. Coverage in Table 2 is the ratio of the number of used clauses that are caused only by maintained clauses to the total number of used clauses that are caused by all clauses. Precision is the ratio of used and held clauses to held clauses; recall is the ratio of used and held clauses to used clauses. In the coverage schema, these values have improved. This indicates that the coverage schema can better identify which clauses will be used. 在覆盖方案中,这些值已经得到了改进。这表明覆盖模式可以更好地确定将使用哪些子句。
|
| 7 Conclusion | We have shown that LBD can identify which clauses will be used, and proposed a concise and lightweight coverage-based reduction strategy, which provides an appropriate LBD threshold in order to cover most propagations and conflicts. The experimental results show that the coverage schema can effectively hold clauses to be used. Many solvers use LBD as an evaluation criterion for learnt clauses. Our approach can be applicable to such solvers. |