文献学习—— Combining Clause Learning and Branch and Bound for MaxSAT

 Combining Clause Learning and Branch and Bound for MaxSAT

 

Chu-Min Li, Zhenxing Xu, Jordi Coll, Felip Manyà, Djamal Habet, Kun He, Combining Clause Learning and Branch and Bound for MaxSAT, in CP-2021, to appear

 

2012 ACM Subject Classification Software and its engineering → Constraints
Keywords and phrases MaxSAT, Branch&Bound, CDCL
Digital Object Identifier 10.4230/LIPIcs.CP.2021.38
Supplementary Material Software (Source Code): https://home.mis.u-picardie.fr/~cli/EnglishPage.html

Funding This work has been partially funded by the French Agence Nationale de la Recherche,
reference ANR-19-CHIA-0013-01, and the Spanish AEI project PID2019-111544GB-C2.

Acknowledgements This work has been partially supported by Archimedes Institute, Aix-Marseille
University. We thank the anonymous reviewers for their comments and suggestions that helped to
improve the manuscript.

---

 

两个重要网址：

https://maxsat-evaluations.github.io/2021/descriptions.html   （文章从这直接进入链接：https://doi.org/10.4230/LIPIcs.CP.2021.38）

https://home.mis.u-picardie.fr/~cli/EnglishPage.html

---

Abstract

Branch and Bound (BnB) is a powerful technique that has been successfully used to solve many combinatorial optimization problems. However, MaxSAT is a notorious exception because BnB MaxSAT solvers perform poorly on many instances encoding interesting real-world and academic optimization problems. This has formed a prevailing opinion in the community stating that BnB is not so useful for MaxSAT, except for random and some special crafted instances. 译文：这在社区中形成了一个普遍的观点，即BnB对MaxSAT不是那么有用，除了随机和一些特殊的设计实例。   In fact, there has been no advance allowing to significantly speed up BnB MaxSAT solvers in the past few years, as illustrated by the absence of BnB solvers in the annual MaxSAT Evaluation since 2017.译文：事实上，在过去几年里，BnB MaxSAT求解器的速度并没有显著提高，从2017年以来的年度MaxSAT评估中没有BnB求解器就可以看出这一点。 Our work aims to change this situation and proposes a new BnB MaxSAT solver, called MaxCDCL, by combining clause learning and an efficient bounding procedure. 译文：我们的工作旨在改变这种情况，并提出了一个新的BnB MaxSAT求解器，称为MaxCDCL，通过结合子句学习和一个有效的边界过程。 The experimental results show that, contrary to the prevailing opinion, BnB can be competitive for MaxSAT. MaxCDCL is ranked among the top 5 solvers of the 15 solvers that participated in the 2020 MaxSAT Evaluation, solving a number of instances that other solvers cannot solve.译文：在参加2020年MaxSAT评估的15家解决方案提供商中，MaxCDCL位列前5名，解决了许多其他解决方案提供商无法解决的实例。 Furthermore, MaxCDCL, when combined with the best existing solvers, solves the highest number of instances of the MaxSAT Evaluations.译文：此外，MaxCDCL与现有的最佳求解器相结合，可以解决MaxSAT计算的最多实例数。

 1 Introduction

	The Maximum satisfiability problem (MaxSAT) is an optimization version of a well-studied and canonical NP-Complete problem, the satisfiability problem (SAT). Although SAT and MaxSAT share many aspects, solving MaxSAT is much harder than solving SAT in practice. 最大可满足性问题(MaxSAT)是一个被广泛研究的典型np完全问题——可满足性问题(SAT)的优化版本。虽然SAT  MaxSAT有很多共同之处，解决MaxSAT比解决SAT在实践中的难度要大得多。
	Indeed, since several clauses can be falsified in an optimal MaxSAT solution, some fundamental SAT techniques such as unit propagation cannot be used in MaxSAT as they are used in SAT. 事实上，由于在一个最佳的MaxSAT解决方案中有几个子句可以被证伪，一些基本的如单元传播等SAT技术不能在MaxSAT中使用，它们能在SAT中被使用。 Despite this difficulty, huge efforts made by researchers make it possible nowadays to solve many interesting real-world and academic NP-hard optimization problems encoded as MaxSAT instances [11, 26]. For this reason, MaxSAT has attracted increasing interest from the academy and industry in recent years. 译文：尽管存在这一困难，但研究人员的巨大努力使许多有趣的现实世界和学术NP-hard优化问题成为可能，这些问题编码为MaxSAT实例[11,26]。因此，近年来，MaxSAT吸引了越来越多的学术界和业界的兴趣。
	As for many NP-hard problems, algorithms for MaxSAT are divided into two categories: exact algorithms, which return optimal solutions and prove their optimality; and heuristic algorithms, which quickly find solutions of good quality without guaranteeing their optimality. This paper will focus on exact algorithms for (unweighted) MaxSAT. 译文： 对于许多NP-hard问题，MaxSAT算法分为两类:精确算法，返回最优解并证明其最优性;以及启发式算法，快速找到质量好的解，而不保证其最优性。本文将重点研究(未加权)MaxSAT的精确算法。
	We roughly distinguish two types of exact algorithms for MaxSAT: branch-and-bound (BnB) algorithms [26], which directly tackle MaxSAT with a bounding procedure, but without unit propagation and clause learning; and SAT-based algorithms [11], which transform MaxSAT into a sequence of SAT instances and call a CDCL (Conflict-Driven Clause Learning) SAT solver to solve them. 译文： 我们大致将MaxSAT的精确算法分为两类:分支定界算法(BnB)算法[26]，它直接用一个边界过程来处理MaxSAT，而不需要单元传播和子句学习;以及基于sat的算法[11]MaxSAT转换为一系列SAT实例，并调用CDCL (Conflict-Driven Clause Learning)SAT解算器。     The performance of SAT-based MaxSAT algorithms is usually much better than BnB MaxSAT solvers in solving many real-world NP-hard optimization problems, because they indirectly exploit clause learning via the SAT solver. 译文：基于SAT的MaxSAT算法在解决许多现实世界NP-hard优化问题时的性能通常比BnB MaxSAT算法要好得多，因为它们间接利用了SAT求解器的子句学习。   Unfortunately,it is hard for a BnB solver to exploit clause learning. 译文：不幸的是，BnB解决者很难利用条款学习。 In a CDCL SAT solver, a backtracking happens only when a clause is falsified, from which a sequence of resolution steps is performed to learn a clause explaining the backtracking.译文：在CDCL SAT求解器中，回溯只发生在一个子句被篡改时，从这个子句中执行一系列解析步骤来学习解释回溯的子句。   However, a BnB MaxSAT solver also need to backtrack when it computes a lower bound equal to the upper bound. In this case, no clause is explicitly falsified, making it hard to learn a clause.译文：然而，BnB MaxSAT求解器在计算下界等于上界时也需要回溯。在这种情况下，没有任何子句被明确伪造，这使得学习子句变得困难。 Probably because of this difficulty, there has been no advance allowing to significantly speed up BnB MaxSAT solvers in recent years, as illustrated by their absence in the annual MaxSAT Evaluation since 2017. 译文：可能正是由于这一困难，近年来BnB的MaxSAT解决方案并没有显著提速，从2017年以来的年度MaxSAT评估中就可以看出这一点。
	In this paper, we propose an original approach that allows a BnB MaxSAT solver to learn a clause when it computes a lower bound equal to the upper bound, together with a new bounding procedure, because the one in current BnB MaxSAT solvers is not adequate for large instances. 译文：在本文中，我们提出了一种新颖的方法，当BnB MaxSAT求解器计算下界等于上界时，允许BnB MaxSAT求解器学习子句，以及一个新的边界过程，因为目前BnB MaxSAT求解器中的边界不适合大实例。 This approach is implemented in a new BnB MaxSAT solver, called MaxCDCL, that combines the new bounding procedure and clause learning.译文：这种方法是在一个新的BnB MaxSAT求解器中实现的，称为MaxCDCL，它结合了新的边界过程和子句学习。 The experimental results show that MaxCDCL is ranked among the top 5 solvers of the 15 solvers that participated in the 2020 MaxSAT Evaluation, solving a number of instances that other solvers cannot solve. Furthermore, MaxCDCL, when combined with the best existing solvers, solves the highest number of instances of the MaxSAT Evaluations.译文：实验结果表明，MaxCDCL在参加2020年MaxSAT评测的15个求解器中位列前5名，解决了许多其他求解器无法解决的实例。此外，MaxCDCL与现有的最佳求解器相结合，可以解决MaxSAT计算的最多实例数。
	Combining clause learning and BnB, as clause learning itself, belongs to the general framework consisting in explaining a failure in the search to avoid the same failure in the future. In other fields such as Pseudo-Boolean Optimization (PBO), there are also works in this framework (e.g. [17]).译文：在其他领域，如伪布尔优化(PBO)，也有这个框架(例如[17]) The general framework is not hard to understand. However, making it effective for solving a particular problem such as SAT or MaxSAT is quite challenging, because this requires a deep understanding of the problem and the related solving techniques.译文：总的框架并不难理解。然而，让它有效地解决特定的问题，如SAT或MaxSAT是相当具有挑战性的，因为这需要对问题和相关的解决技术的深入理解。 So, one important contribution of our work is that we found a configuration and an efficient implementation of this configuration allowing to make the combination of clause learning and BnB effective for MaxSAT, as presented in this paper. 译文：因此，我们工作的一个重要贡献是，我们找到了一种配置和这种配置的有效实现，使子句学习和BnB的组合对MaxSAT有效，如本文所述。
	译文：更重要的是，我们的研究结果反驳了该领域的主流观点，即尽管BnB是一个强大的技术，已经成功地解决了许多组合优化问题，但它对MaxSAT没有太大的用处。作为首个成功利用子学习的BnB MaxSAT求解器，MaxCDCL开辟了广阔的研究方向。 More importantly, our results refute a prevailing opinion in the field stating that, although BnB is a powerful technique that has successfully been used to solve many combinatorial optimization problems, it is not so useful for MaxSAT. Indeed, as the first BnB MaxSAT solver successfully exploiting clause learning, MaxCDCL opens promising research directions.
	译文：本文的组织形式如下:第2节为论文的初步准备。第3节回顾了最先进的MaxSAT解决方案。第4节描述了MaxCDCL。第五部分对MaxCDCL进行了实证评价和分析。第六节总结。 This paper is organized as follows: Section 2 presents the preliminaries. Section 3 reviews state-of-the-art MaxSAT solvers. Section 4 describes MaxCDCL. Section 5 empirically evaluates and analyzes MaxCDCL. Section 6 concludes.

 2 Preliminaries

	A propositional variable x can take values 0 or 1 (false or true). A literal is a variable x or its negation ¬x. A clause is a disjunction of k literals l1 ∨ · · · ∨ lk. A propositional formula in Conjunctive Normal Form (CNF) is a conjunction (or a set) of m clauses c1, . . . , cm. An assignment of truth values to the propositional variables satisfies a literal x if x = 1, and satisfies a literal ¬x if x = 0. A literal x or ¬x is assigned if x is assigned a value, otherwise it is free. An assignment is complete if all the variables are assigned a value, otherwise it is partial. A (partial) assignment is usually represented by a (sub)set of satisfied literals. A clause is satisfied if at least one of its literals is satisfied. A CNF is satisfied if all its clauses are satisfied. The Boolean satisfiability (SAT) problem for a CNF ϕ is to determine whether there exists an assignment that satisfies ϕ.
	MaxSAT is the problem of finding an assignment that satisfies the maximum number of clauses in a given multiset of clauses. In partial MaxSAT, there are hard and soft clauses, and the goal is to satisfy all the hard clauses and the maximum number of soft clauses. In weighted (partial) MaxSAT, each soft clause has a cost to pay if it is violated. This paper will focus exclusively on unweighted (partial) MaxSAT. weighted (partial) MaxSAT unweighted (partial) MaxSAT
	The state-of-the-art SAT solvers implement the CDCL algorithm. CDCL alternates a search phase, where literals are assigned until either a solution or a conflict is found, and a learning phase, which is executed after finding a conflict in order to learn a new clause. Unit Propagation (UP) is the main inference rule applied during the search: If there is a unit clause {l} in ϕ, literal l must be satisfied (i.e., set to 1). Then, any clause containing l is removed from ϕ, and all the occurrences of ¬l in clauses of ϕ are (implicitly) removed. UP is applied during the search until an empty clause (conflict) is found or no unit clause exists in ϕ. If UP finishes without finding a conflict, a new literal is picked following a heuristic and is set to 1 (we make a decision), and UP is applied again. If all the variables are assigned without finding a conflict, ϕ is satisfiable. The decision level of an assigned literal is the number of decisions made before being assigned. When a conflict is found, a conflict analysis is performed on the implication graph to derive a new clause explaining the conflict.
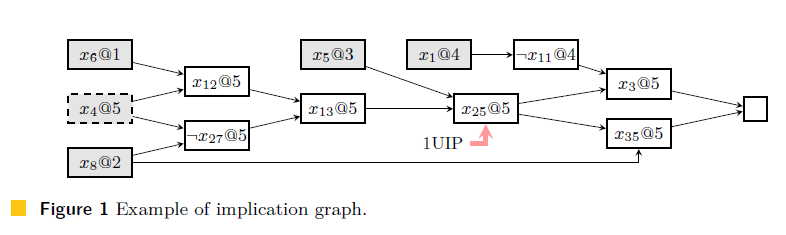
	When a conflict is found in the decision level dl (i.e., dl decisions were made before the conflict is found), a node in the decision level dl is said active if it is not the 1UIP but is in a path from the 1UIP to the conflict. In other words, the active nodes are those nodes that allow to reach the conflict from the 1UIP in the decision level dl. For example, in Figure 1, a conflict is found in the decision level 5, and x3@5 and x35@5 are active nodes. The 1UIP learning schema identifies, in each path from a node in a decision level lower than dl to an active node, the last literal in the lower decision level. The new learnt clause is composed of the negation of these literals and the 1UIP. For instance, in Figure 1, clause ¬x8 ∨ x11 ∨ ¬x25 is learnt, because there are two paths from lower decision levels to an active node, in which x8 and ¬x11 are the last literals in lower decision levels, respectively.
	Figure 1 shows an example of implication graph. It is a directed acyclic graph where each node represents an assignment l@dl, where l is a literal set to 1 and dl is its decision level. The negations of the literals of incoming edges of a node l@ld represent the reason (clause) why UP has set l = 1. For instance, node x12@5 is propagated due to clause ¬x6 ∨ ¬x4 ∨ x12 (i.e., x6 ∧ x4 → x12), given that x4 and x6 have been set to 1. A node without incoming edges represents a decision. All decisions are painted in grey, and the last one is dashed. A conflicting clause is represented by incoming edges to □; in this example, clause ¬x3 ∨ ¬x35. A Unique Implication Point (UIP) is a node of the implication graph that belongs to all paths from the last decision to the conflict. Figure 1 contains three UIPs: the last decision x4, and literals x13 and x25. The most used learning schema in CDCL SAT solvers is called first UIP (1UIP), guided by the closest UIP to the conflict in the implication graph.
	The learnt clause explains the conflict: when all its literals are falsified, unit propagation reproduces the implication graph to derive the same conflict. So, adding the learnt clause prevents the same conflict in the future search. After learning a clause, CDCL backtracks to the second highest decision level of the learnt clause (level 4 in the above example). Unsatisfiability is determined when a conflict is found at decision level 0.

3 Related Work

	A major difference between MaxSAT and SAT solvers is that each clause must be satisfied in a SAT solution while a soft clause can be falsified in an optimal MaxSAT solution, making MaxSAT much harder to solve than SAT in practice. Despite this, the MaxSAT community has made huge efforts to implement exact MaxSAT solvers with impressive performance over the last decade [11, 26]. On the other hand, heuristic MaxSAT algorithms such as SatLike [25] have also been proposed.
	Roughly speaking, we find two main groups of exact MaxSAT solvers: branch-and-bound (BnB) and SAT-based solvers. branch-and-bound (BnB) SAT-based solvers   BnB MaxSAT solvers implement the branch-and-bound scheme and incorporate a lookahead procedure that detects inconsistent subsets of soft clauses by applying unit propagation and computes a lower bound [26]. 译文：MaxSAT求解器实现了分支定界方案，并结合了一个前瞻过程，通过应用单元传播来检测软子句的不一致子集，并计算一个下界[26]。     They also apply some inference rules at each node of the search tree. 译文：它们还在搜索树的每个节点上应用一些推理规则。 Representative BnB solvers are MaxSatz [30], MiniMaxSat [20], Ahmaxsat [1, 14] and Akmaxsat [24]. Closely related to MaxSAT, we can find BnB solvers for the Weighted Constraint Satisfaction Problem (WCSP). 译文：与MaxSAT密切相关，我们可以找到加权约束满足问题(WCSP)的BnB解。   Recently, it was presented a technique to improve BnB WCSP solving by avoiding branching on variables which are unlikely to increase the lower bound [43]. 译文：最近，有人提出了一种改进BnB WCSP求解的技术，方法是避免对不太可能增加下界[43]的变量进行分支。
	SAT-based MaxSAT solvers proceed by reformulating the MaxSAT optimization problem into a sequence of SAT decision problems [11]. 译文：基于SAT的MaxSAT求解器将MaxSAT优化问题重新表述为一系列SAT决策问题[11]。 These solvers could still be divided into three subgroups: model-guided, core-guided and Minimum Hitting Sets (MHS-)guided.   model-guided core-guided Minimum Hitting Sets (MHS-)guided.   Model-guided approaches reduce to SAT the problem of deciding whether there exists an assignment for the MaxSAT instance with a cost less than or equal to a certain k, and successively decrease k until an unsatisfiable SAT instance is found. 译文：模型导向方法将判断MaxSAT实例是否存在赋值且其代价小于或等于某k的问题简化为SAT，并依次减小k，直到找到不满足的SAT实例。 Among such solvers we find SAT4J-Maxsat [12], QMaxSat [23, 44], Open-WBO [37] or Pacose [40].   Core-guided and MHS-guided approaches consider a MaxSAT instance as a SAT instance and call a CDCL SAT solver to identify an unsatisfiable subset of soft clauses, called a core.  Core-guided和mhs引导的方法考虑MaxSAT实例作为一个SAT实例，并调用CDCL SAT求解器识别出一个软子句的不可满足子集，称为核心子句。   Then, they relax this core and solve the relaxed instance with a CDCL SAT solver to identify another core, repeating this process until deriving a satisfiable instance. 译文：然后，他们放松这个核心，并使用CDCL SAT求解器解决放松的实例，以识别另一个核心，重复这个过程，直到得到一个满意的实例。   The difference between them is that core-guided solvers relax a core using cardinality constraints, while MHS-guided solvers remove one clause from each detected core so that the number of different clauses removed from the cores is minimized by solving a minimum hitting set instance with an integer programming solver. 译文： 它们之间的区别是，核心引导的求解器使用基数约束放松一个核心，而mhs引导的求解器从每个检测到的核心中删除一个子句，从而通过求解一个最小命中集实例来最小化从核心中删除的不同子句的数量整数规划求解器进行求解。 The most representative core-guided solvers include msu1.2 [36], WBO [35], Open-WBO [37], WPM1 [3], PM2 [5], WPM2 [4], WPM3 [6], Eva [39], RC2 [21], and the most representative MHS-guided solvers include MHS [41] and MaxHS [8, 10, 15, 16].   Core-guided search has also been extended to constraint programming [19]. 译文：核心引导搜索也被扩展到约束规划[19].
	A common point of SAT-based MaxSAT solvers is that they indirectly exploit the clause learning technique by repeatedly calling a CDCL SAT solver.  译文：基于SAT的MaxSAT求解器的一个共同点是，它们通过反复调用CDCL SAT求解器间接利用子句学习技术。     Unfortunately, it is hard for BnB solvers to exploit clause learning, which might explain their poor performance on real-world optimization problems. 译文：不幸的是，BnB求解器很难利用子句学习，这可能解释了它们在现实世界的优化问题上表现不佳的原因。 We are aware of only one tentative in [2]: when the number of falsified soft clauses reaches the upper bound, the falsification of these soft clauses is analyzed to learn a clause. Nevertheless, no clause is learnt when the lookahead procedure returns a lower bound equal to the upper bound, and the reported results are not competitive. 译文：我们知道在[2]中只有一个试探性:当证伪软子句的数量达到上限时，分析这些软子句的证伪来学习一个子句。然而，当前瞻过程返回的下界等于上界，并且报告的结果不是竞争性的时，就不会学习子句。

4 MaxCDCL: A BnB Algorithm Using CDCL for MaxSAT

	This section first presents the general structure of MaxCDCL, and then the different components of our approach implemented in MaxCDCL. 译文：本节首先介绍MaxCDCL的一般结构，然后介绍在MaxCDCL中实现的方法的不同组件.
	4.1 General Structure of MaxCDCL
	We distinguish between hard and soft conflicts in the MaxSAT context. A hard conflict occurs when the current partial assignment falsifies a hard clause. Given an upper bound UB, a soft conflict occurs when the current partial assignment cannot be extended to a complete one falsifying fewer than UB soft clauses. A CDCL SAT solver only considers hard conflicts, learns a hard clause from each hard conflict and backtracks. A BnB CDCL MaxSAT solver extends the CDCL SAT solver by also learning a hard clause from each discovered soft conflict and backtracks. Algorithm 1 depicts such a BnB CDCL MaxSAT solver called MaxCDCL.
	Given a MaxSAT instance with a set of hard clauses and a set of soft clauses, MaxCDCL works with H and S, where H contains the hard clauses and S contains a new literal y for each soft clause sc after adding the hard clauses encoding y ↔ sc to H. We call such y soft literal, because it represents a soft clause (i.e., a soft literal is satisfied if and only if the corresponding soft clause is satisfied). To solve the MaxSAT instance, MaxCDCL is repeatedly called with UB= 20, 21, 22, 23, . . . without exceeding |S| + 1 or UBf + 1 where UBf is a feasible upper bound computed by a heuristic solver with a short cutoff. This process stops when it obtains an assignment satisfying all clauses in H and falsifying fewer than UB soft literals in S. After that, MaxCDCL is repeatedly called with UB set to the number of falsified soft literals in the previous call, until no better solution can be found.
	MaxCDCL is like a CDCL SAT solver except for two points. First, when UP does not falsify any hard clause in the UPLA procedure, it calls, under certain condition, a lookahead (LA) procedure to compute a lower bound |cores| of the number of soft literals that will be falsified if the current partial assignment is extended. If a soft conflict is discovered, i.e., if |falseS| + |cores| ≥UB, it is analyzed to learn a clause for backtracking. Second, if no soft conflict is discovered, but it is discovered that the falsification of any free soft literal y not used in |cores| would result in a soft conflict, y is satisfied by a procedure called hardening.
	Note that model-guided MaxSAT solvers also set a UB in their search. However, they do not compute a lower bound to discover soft conflicts as MaxCDCL. Consequently, MaxCDCL is able to backtrack much earlier than model-guided MaxSAT solvers for a given UB. See the next subsection for details and illustrative examples.
	Algorithm 1 MaxCDCL(H, S,UB), a generic CDCL procedure with lookahead for MaxSAT.
	4.2 Combining Lookahead and Clause Learning
	Proposition 2 provides the foundation of our approach in the general case.
	4.3 A Probing Strategy for Lookahead
	Existing BnB MaxSAT solvers usually tackle random or crafted instances of limited size and look ahead at each branch. However, such a treatment might be too costly and useless for large instances. If the lower bound is not tight enough to prune the current branch, the time spent to compute the lower bound is lost. When k = UB−|falseS|, the lookahead procedure has to detect k disjoint local cores to be successful. Generally, the greater the value of k, the lower the probability of lookahead to be successful.
	MaxCDCL uses a probing strategy to determine if lookahead has to be applied at the current branch. With probability p, where p is a parameter intuitively fixed to 0.01, lookahead is applied for probing purpose. The mean avgp and the standard deviation devp of the number of detected disjoint local cores in a successful probing lookahead are computed (not shown here due to the lack of space) to select the branches where lookahead is applied.
	Inspired by the 68-95-99.7 rule in statistics, which says that the values within one (two, three) standard deviation of the mean account for about 68% (95%, 99.7%) of a normal data set, we reasonably assume that the number of cores detected in a successful lookahead is probably lower than avgp + coef ∗ devp when coef = 3. So, lookahead is not applied at the current branch when k > avgp + coef ∗ devp. However, since the probing may not get exact information and the values may not follow a perfect normal distribution, coef is dynamically adjusted to maintain the success rate of lookahead between lowRate and highRate, where lowRate and highRate are parameters intuitively fixed to 0.6 and 0.75, respectively.
	Concretely, coef is initialized to 2 for each UB. At each probing, if the success rate of lookahead since the last probing is greater than highRate, it is increased by 0.1; and if it is lower than lowRate, it is decreased by 0.1. There are no lower and upper bounds on coef. When it is too low so that no lookahead is performed between two probings, it is reset to 2.
	4.4 Soft literal ordering in lookahead
	Existing BnB MaxSAT solvers such as MaxSatz usually propagate soft unit clauses in the ordering these clauses become unit, or in their ordering in the input formula when detecting disjoint cores [28]. MaxCDCL propagates first the soft literals in the cores detected in the previous lookahead. We use this ordering for two intuitive reasons.
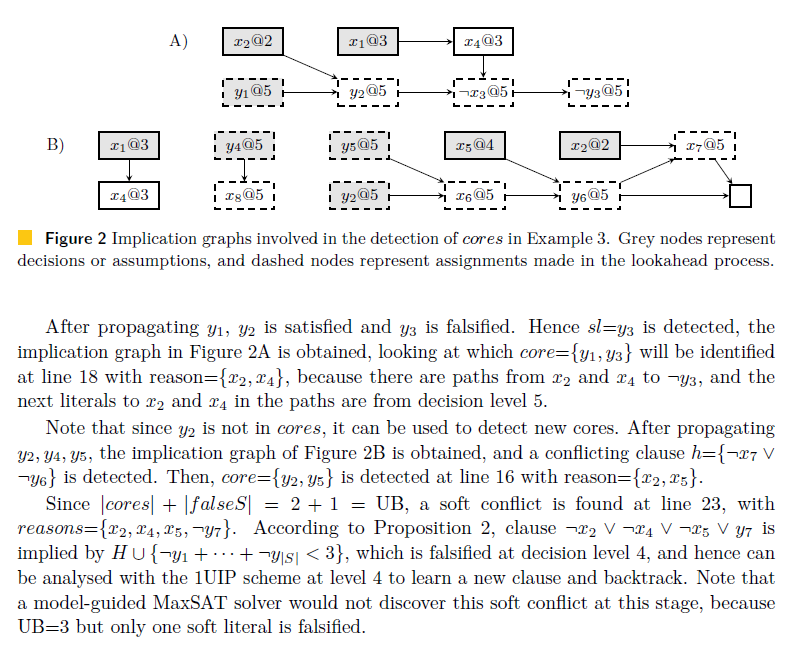
	Before backtracking, a local core detected in the previous lookahead remains to be a core. Re-detecting a previous local core allows to obtain a possibly smaller local core due to additional assignments. After backtracking, re-detecting local cores in the previous soft conflict may allow to detect a new soft conflict sharing many local cores with the previous conflict. In this way, the clauses learnt from consecutive soft conflicts allow to intensify the search, because the clause learnt from a soft conflict is derived from the reasons of the detected cores.
	The quality of a clause learnt from a soft conflict highly depends on the detected cores, which in turn highly depends on the soft literal ordering. How to improve the quality of the learnt clause by further improving the soft literal ordering definitely deserves future study.
	4.5 Improving the VSIDS heuristic by lookahead
	When there is no unit clause, a CDCL SAT solver chooses a free literal l using a decision heuristic, satisfies l and then performs unit propagation. VSIDS [38] is one of the widely used decision heuristics: it initializes the score of each variable to 0, and then at each conflict, it increases the score of each variable in a path to the conflict in the implication graph by var_inc, where var_inc is initialized to 1 and, after each conflict, it is divided by a parameter usually set to 0.95 to give more importance to the next conflict. Note that VSIDS is a heuristic based on lookback, because it is based on the conflicts in the past.
	VSIDS is also used in MaxCDCL by increasing the score of a variable in a soft or hard conflict as in a CDCL SAT solver, but is modified as follows by taking lookahead into account. Every time the lookahead procedure detects a local core, the score of the variables encountered when identifying the reason of the core (see Subsection 4.2) is increased by var_inc × γ, where γ is a discount-rate parameter as in reinforcement learning, and is empirically fixed to 0.1. The intuition of this modification is the following. A soft conflict is derived when UB local cores are detected. So a variable contributing to many local cores should be favoured to reach a soft conflict as early as possible. However, a local core represents only a component of a future possible soft conflict but not a soft conflict for sure. So the increase of the score of a variable contributing to a core should be discounted by γ.
	4.6 Implementation of MaxCDCL
	Since MaxCDCL can be considered as an extension of a CDCL SAT solver, it is implemented on top of the CDCL SAT solver MapleCOMSPS_LRB [32], winner of the application track of SAT competition 2016. We chose MapleCOMSPS_LRB because it was one of the best SAT solvers with deterministic behavior when we started this work in 2017. Nevertheless, some of the recent advances in SAT solving are incorporated, including1:
	The approach from [31, 34] is applied to minimize the learnt clauses. The clause size reduction with the all-UIP learning technique from [18] is applied to reduce the clauses learnt from soft conflicts. This technique is particularly useful for MaxCDCL, because a clause learnt from a soft conflict is usually longer than a clause learnt from a hard conflict. The all-UIP technique allows to significantly reduce the size of a clause learnt from a soft conflict. The learnt clause management technique proposed in [22] is incorporated into MaxCDCL, allowing more learnt clauses to be kept in the clause database.
	We plan to implement MaxCDCL on top of Kissat [13], the winner of the SAT2020 competition, which might further improve its performance. 译文：我们计划在SAT2020竞赛的获胜者Kissat[13]上实施MaxCDCL，这可能会进一步提高其性能。

 

5 Experimental Evaluation

	We report on an experimental investigation to assess the performance of MaxCDCL. We ran all experiments with Intel Xeon CPUs E5-2680@2.40GHz under Linux with 32GB of memory, using the following benchmark sets, unless otherwise stated:
	MSE19∪20: The union of all the instances used in the complete unweighted track of the MaxSAT Evaluations (MSE) 2019 and 2020, a total of 1000 distinct instances. MC: A subset of the Master Collection of instances from the MaxSAT evaluations held until 2019 2. It contains 16080 unweighted (partial) MaxSAT instances, classified into 51 families and 76 subfamilies. MC includes all the instances of the 63 subfamilies having 100 instances or less, and the first 100 instances as they occur in the natural order in each of the remaining 13 subfamilies, considering a total of 3614 instances. This selection provides a simple, deterministic and objective criterion that does not favor any solver; and the experiments can be easily reproduced. MC contains 726 instances that also belong to MSE19∪20.
	The cutoff time is one hour (3600s) per instance as in the MaxSAT Evaluation. For MaxCDCL and its variants, this includes 60 seconds to find a feasible upper bound UBf with SatLike (version 3.0). Note that MaxCDCL and its variants do not start the search
	5.1 MaxCDCL Components
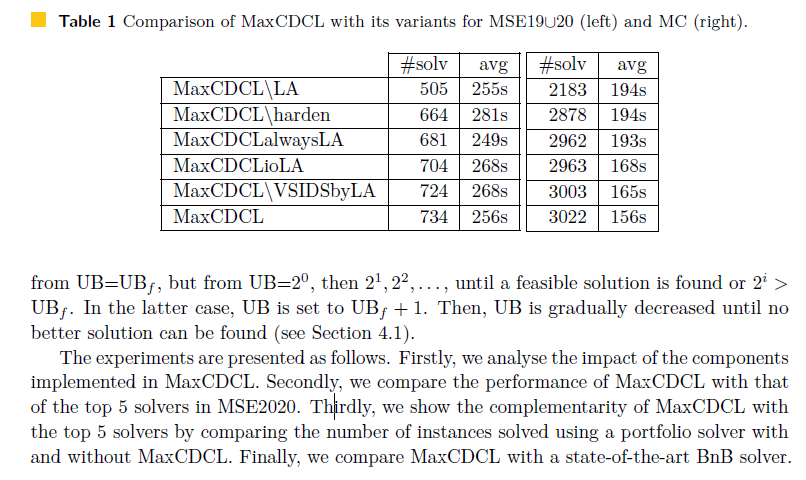
	Table 1 compares MaxCDCL with the following variants: MaxCDCL\LA. MaxCDCL without lookahead, i.e. the condition to lookahead is never satisfied in line 3 of Algorithm 2. Note that after finding a feasible UB, MaxCDCL\LA performs linear SAT-UNSAT search as a model-guided SAT-based MaxSAT solver. MaxCDCL\harden. MaxCDCL without hardening (i.e., lines 17 and 18 in Algorithm 1 are removed). MaxCDCLalwaysLA. MaxCDCL that looks ahead at every branch, i.e., the condition to lookahead is always satisfied in line 3 of Algorithm 2. MaxCDCLioLA. MaxCDCL that, when detecting cores in lookahead, always propagates the soft literals in the ordering as the corresponding soft clauses occur in the input instance. MaxCDCL\VSIDSbyLA. MaxCDCL that does not increase the VSIDS score of the variables contributing to a local core detected in lookahead as described in Subsection 4.5.
	In Table 1, columns “#solv” give the number of solved instances and columns “avg” give the mean time in seconds (including the 60s used by SatLike) needed to solve these instances. These results indicate that a careful configuration combining clause learning and BnB is crucial for the performance of MaxCDCL, including: hardening based on local core detection and clause learning, the selective and adaptive application of lookahead and the ordering to propagate the soft literals when detecting local cores, because the absence of any of these components makes a significant number of instances out of reach of MaxCDCL. Without this configuration, MaxCDCL\LA solves 229 instances less than MaxCDCL in MES19∪20 and 839 instances less than MaxCDCL in MC. Note that although the hardening of a soft literal requires a distinct learnt clause, it does not increase the total memory usage, because it allows to avoid many learnt clauses by reducing search space.
	Recall that the most fundamental feature of MaxCDCL is the clause learning from soft conflicts. We computed the average length of a clause learnt from a soft (hard) conflict for each solved instance by MaxCDCL in MSE19∪20, and found that the median average length  of a clause learnt from a soft (hard) conflict is 23.67 (19.2) among the 734 instances solved in the set. Note that the learnt clause length averaged across the 734 instances does not make sense because it is biased by few instances with very long learnt clause length.
	In addition, the comparison of MaxCDCL with MaxCDCL\VSIDSbyLA suggests that the VSIDS heuristic might be improved by lookahead, indicating a promising research direction.
	To complete the subsection, we mention the impact of two other components of MaxCDCL: (1) the local search by SatLike in preprocessing to compute a feasible UB allows MaxCDCL to solve 8 more instances in MSE19∪20; (2) the sequential cardinality constraint encoding is applied to about the 20% of the instances in MSE19∪20 for at least one UB, helping solve 39 extra instances in MSE from highly symmetric problems such as drmx-at-most-k.
	5.2 Comparison with the top 5 Solvers in MSE2020
	A total of 15 solvers competed in the complete unweighted track of MSE2020 [9]. We consider the top 5 solvers: MaxHS (mhs in short), which is MHS-guided; EvalMaxSAT (eval in short), RC2-B (rc2 in short) and open-wbo-res-mergesat-v2 (Open-WBO or owbo in short), which are core-guided; and UWrMaxSAT (uwr in short), which combines both core-guided and model-guided solving. We executed the versions used in MSE2020 in all the experiments.
	Table 2 shows the results for MSE19∪20 and MC, respectively. Column “#uniq” has the number of instances that were only solved by the solver in the row. Column “#win” has the number of instances solved by MaxCDCL but not by the solver in the row.
	We observe that MaxCDCL solves more instances than two top 5 solvers in MSE19∪20 and four top 5 solvers in MC. More importantly, MaxCDCL solves a significant number of instances that other solvers cannot solve. For example, MaxCDCL solves 116 instances in MC that MaxHS does not solve. If we consider all the solvers together, there is also a significant number of instances solved by MaxCDCL that no other solver is able to solve: 16 instances in MSE19∪20 and 67 instances in MC that mainly come from the subfamilies MaxClique, MaxCut and UAQ. These results show that the existing MaxSAT solvers, especially the model-guided and core-guided ones, are able to solve similar kinds of instances. Nevertheless, MaxCDCL has the potential to solve new kinds of instances that are not solvable with the current MaxSAT techniques. It is important to note that MaxCDCL is far from being as optimized as the other solvers, which are the result of a process of continuous improvements since more than ten years.
	5.3 Combining MaxCDCL with existing solvers
	Given two deterministic solvers X and Y and a time limit T to solve an NP-hard problem such as MaxSAT, the simplest way to try to solve more instances than X and Y alone within the time limit T is to combine X and Y by running X within the time limit T/2, and then Y from scratch within the remaining time T/2 if the instance is not solved by X.
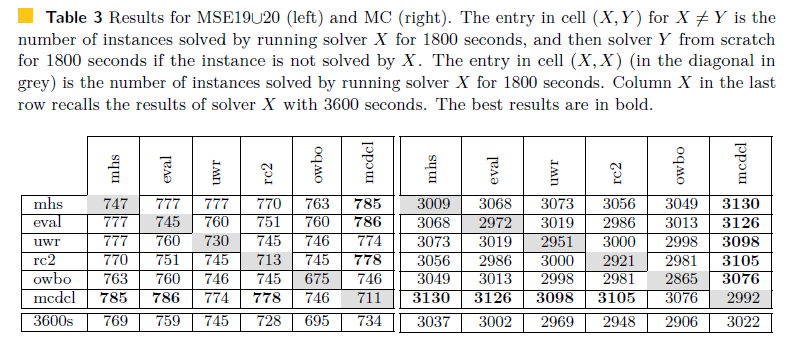
	Table 3 shows the results of all possible pairwise combinations of the top 5 solvers and MaxCDCL (mcdcl) in MSE2020 for T = 3600s. Each cell (X, Y ) for X ̸= Y contains the number of instances solved by running solver X for 1800s and then solver Y from scratch for 1800s in MSE19∪20 (left) and MC (right). Each cell (X,X) (in the diagonal in grey) contains the number of instances solved by X in 1800s. Column X in the last row recalls the results of X with 3600 seconds. Combining any of the top 5 solvers with MaxCDCL solves more instances than this solver and MaxCDCL alone within 3600s, while this is not always true when combining two top 5 solvers. For example, combining MaxHS and Open-WBO solves 763 instances in MSE19∪20 within 3600s, while MaxHS alone solves 769 instances within 3600s. This shows that MaxCDCL is more complementary with the top 5 solvers than other solvers.
	More importantly, MaxCDCL combined with the top 2 solvers, MaxHS and EvalMaxSAT, solves the highest numbers (785 and 786) of instances in MSE19∪20. This result is significantly better than that of MaxHS or EvalMaxSAT alone, and the best combination without MaxCDCL solves only 777 instances. The results are even more striking in MC, where the worst combination of MaxCDCL with a top 5 solver is better than any other combination not including MaxCDCL, and combining MaxHS and MaxCDCL gives the best results, solving 93 instances more than the previous best result achieved by MaxHS alone, and 57 instances more than the best combination without MaxCDCL.
	Figure 3 shows cactus plots comparing the best two combinations of solvers with Max- CDCL, the best two combinations without MaxCDCL, as well as the best two mono-solvers, for MSE19∪20 (left) and MC (right). Other solvers and combinations are excluded for readability reasons. For any time T (0 < T ≤ 3600s), a curve gives the number of instances solved by a mono-solver or a combination of two solvers within T, where the number of instances solved by a combination X-Y of solvers X and Y within T is the number of instances solved by running X for T/2, and then Y for T/2. The solving time of a combination X-Y of solvers X and Y for an instance is twice the minimum solving time among X and Y . This simulates a parallel execution of X and Y by alternating them in small time periods. The plots clearly show the advantage of combining an existing solver with MaxCDCL, allowing to solve the highest number of instances within 3600s, and the advantage becomes greater as the running time is increased.
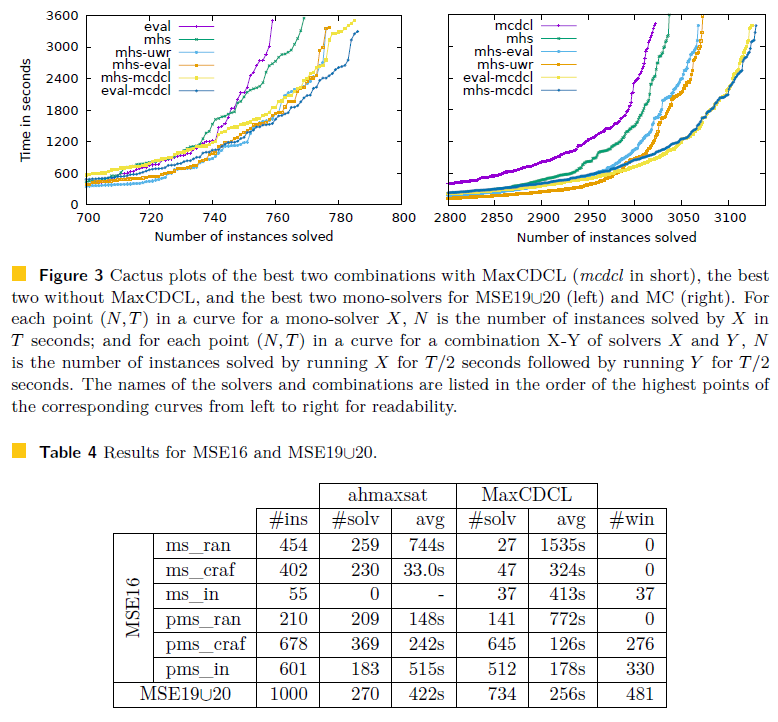
	5.4 Comparison with a BnB Solver
	We compare MaxCDCL with ahmaxsat, which was the best BnB solver in the last MaxSAT evaluation (MSE2016) in which BnB solvers competed. We use the MSE2016 instances of the categories MaxSAT (ms) and partial MaxSAT (pms). Each category has random (ran), crafted (craf), and industrial (in) instances. Thus, we consider a total of 6 families. 译文：我们比较了MaxCDCL和ahmaxsat，后者是上届MaxSAT评估(MSE2016)中BnB解算器竞争的最佳解算器。我们使用类别MaxSAT (ms)和部分MaxSAT (pms)的MSE2016实例。每个类别都有随机的(运行的)、手工的(工艺的)和工业的(在)实例。因此，我们总共考虑6个家庭。
	The results are shown in Table 4, where the number of instances for each family is given in column “#ins”. We observe that ahmaxsat solves more random and non-partial crafted instances. A learnt clause for these instances with randomness and limited size usually contains most of the variables of the instances and is hardly useful. So, the higher use of lower bounding methods and the lack of clause learning in ahmaxsat are adequate for them, and the higher use of lower bounding methods (like in MaxCDCLalwaysLA) does not improve MaxCDCL for them because of clause learning. However, ahmaxsat has poor performance on other instances. Instead, MaxCDCL solves a much higher number of such instances.

6 Conclusion

	We described MaxCDCL, a MaxSAT solver that combines, for the first time to the best of our knowledge, branch and bound and clause learning. The main differences of MaxCDCL with existing SAT-based MaxSAT solvers are the following: 译文：我们第一次描述了MaxCDCL，一个MaxSAT求解器，它结合了我们所知道的最好的分支和约束以及子句学习。 译文：MaxCDCL与现有基于sat的MaxSAT求解器的主要区别如下:
	SAT-based MaxSAT solvers use a CDCL SAT solver as a black box and do not interfere in the internal operations of the SAT solver when solving an instance, while MaxCDCL itself can be considered a SAT solver extended to handle soft conflicts. Both MaxCDCL and model-guided MaxSAT solvers have an upper bound UB−1 of the number of soft clauses that can be falsified. The difference lies in how to exploit this UB. Let falseS denote the set of already falsified soft clauses. On the one hand, model-guided MaxSAT solvers call a SAT solver after encoding UB into CNF. If no hard clause is falsified, the SAT solver backtracks only after |falseS| ≥ UB, because no clause encoding UB is falsified if |falseS| < UB. On the other hand, MaxCDCL computes a lower bound LB of the number of soft clauses that will be falsified (but not yet falsified), and backtracks as soon as LB+|falseS| ≥ UB. Thus, MaxCDCL is able to backtrack much earlier than model-guided MaxSAT solvers. MaxCDCL, core-guided or MHS-guided MaxSAT solvers all identify cores. However, a core-guided or MHS-guided MaxSAT solver only identifies global cores (i.e., the cores that do not depend on any partial assignment) in order to relax them, while MaxCDCL detects local cores by using UP under a partial assignment to derive a soft conflict for learning a clause and backtracking early. Note that identifying a global core is NP-hard, while detecting a local core by applying UP is polynomial.
	The extensive experimentation conducted shows that MaxCDCL is ranked among the top 5 exact MaxSAT solvers in the 2020 MaxSAT evaluation. Furthermore, it solves a significant number of instances that other solvers cannot solve, suggesting that combining branch and bound and clause learning has the potential to solve new kinds of instances that are not solvable with current MaxSAT techniques. More importantly, combining MaxCDCL with the existing solvers allows to solve the highest number of MaxSAT instances.
	Detailed analyses indicate that the performance of MaxCDCL comes from a careful configuration combining clause learning and BnB, including hardening based on local core detection and clause learning, the selective and adaptive application of lookahead, and the ordering to propagate the soft literals when detecting local cores.
	We believe that the proposed approach opens new and promising research directions, including for example: (1) improving the quality of the clauses learnt from soft conflicts by designing new soft literal orderings in lookahead; (2) exploiting the relationship of SAT and MaxSAT for improving SAT and MaxSAT solving; (3) adapting the approach of MaxCDCL to other problems such as pseudo-Boolean optimization and Max-CSP; (4) extending MaxCDCL to weighted MaxSAT, in which each soft clause is weighted. In the extension of MaxCDCL to weighted MaxSAT, each soft clause is represented by a weighted soft literal. A local core detected by lookahead is weighted by the minimum soft literal weight it contains, and other weights are split to be used in other core detections. When the total weight of all detected local cores reaches UB, a soft conflict is discovered. The challenge here is that there can be more local cores to detect than in the unweighted case. Thus, the clause learnt from a soft conflict can be longer. Special strategies in clause and soft literal ordering should be designed to learn shorter clauses from soft conflicts.

References

1 André Abramé and Djamal Habet. Ahmaxsat: Description and evaluation of a branch and bound Max-SAT solver. J. Satisf. Boolean Model. Comput., 9:89–128, 2014. 2 André Abramé and Djamal Habet. Learning nobetter clauses in Max-SAT branch and bound solvers. In Proceedings of ICTAI 2016, pages 452–459, 2016. 3 Carlos Ansótegui, María Luisa Bonet, and Jordi Levy. Solving (Weighted) Partial MaxSAT through satisfiability testing. In Proceedings of SAT 2009, pages 427–440. Springer LNCS 5584, 2009. 4 Carlos Ansótegui, María Luisa Bonet, and Jordi Levy. A new algorithm for weighted partial MaxSAT. In Proceedings AAAI 2010, pages 3–8, 2010. 5 Carlos Ansótegui, Maria Luisa Bonet, and Jordi Levy. SAT-based MaxSAT algorithms. Artificial Intelligence, 196:77–105, 2013. 6 Carlos Ansótegui and Joel Gabàs. WPM3: An (in)complete algorithm for Weighted Partial MaxSAT. Artificial Intelligence, 250:37–57, 2017. 7 Gilles Audemard and Laurent Simon. Predicting learnt clauses quality in modern SAT solvers. In Proceedings IJCAI 2009, pages 399–404, 2009. 8 Fahiem Bacchus. MaxHS in the 2020 MaxSAT Evaluation. In MaxSAT Evaluation 2020: Solver and Benchmark Descriptions, pages 19–20, 2020. 9 Fahiem Bacchus, Jeremias Berg, Matti Järvisalo, and Ruben Martins. MaxSAT Evaluation 2020: Solver and benchmark descriptions, 2020. 10 Fahiem Bacchus, Antti Hyttinen, Matti Järvisalo, and Paul Saikko. Reduced cost fixing in MaxSAT. In Proceedings of CP 2017, Springer LNCS, pages 641–651, 2017. 11 Fahiem Bacchus, Matti Järvisalo, and Martins Ruben. Maximum satisfiability. In Handbook of satisfiability, second edition, pages 929–991. IOS Press, 2021. 12 Daniel Le Berre and Anne Parrain. The Sat4j library, release 2.2. J. Satisf. Boolean Model. Comput., 7(2-3):59–6, 2010. 13 Armin Biere, Katalin Fazekas, Mathias Fleury, and Maximilian Heisinger. CaDiCaL, Kissat, Paracooba, Plingeling and Treengeling entering the SAT Competition 2020. In Proceedings of SAT Competition 2020: Solver and Benchmark Descriptions, page 50, 2020. 14 Mohamed Sami Cherif, Djamal Habet, and André Abramé. Understanding the power of Max-SAT resolution through UP-resilience. Artificial Intelligence, 289:103397, 2020. 15 Jessica Davies and Fahiem Bacchus. Solving MAXSAT by solving a sequence of simpler SAT instances. In Proceedings of CP 2011, page 225–239. Springer, 2011. 16 Jessica Davies and Fahiem Bacchus. Exploiting the power of MIP solvers in MAXSAT. In Proceedings of SAT 2013, pages 166–181. Springer, 2013. 17 Jo Devriendt, Ambros Gleixner, and Jakob Nordström. Learn to relax: Integrating 0-1 integer linear programming with pseudo-boolean conflict-driven search. Constraints, pages 1–30, 2021. 18 Nick Feng and Fahiem Bacchus. Clause size reduction with all-uip learning. In Proceedings of SAT 2020, Springer LNCS 12178, pages 28–45, 2020. 19 Graeme Gange, Jeremias Berg, Emir Demirović, and Peter J Stuckey. Core-guided and core-boosted search for CP. In Proceedings of CPAIOR 2020, pages 205–221, 2020. 20 Federico Heras, Javier Larrosa, and Albert Oliveras. MiniMaxSAT: An efficient Weighted Max-SAT solver. Journal of Artificial Intelligence Research, 31:1–32, 2008. 21 Alexey Ignatiev, António Morgado, and João Marques-Silva. RC2: an efficient maxsat solver. J. Satisf. Boolean Model. Comput., 11(1):53–64, 2019. 22 Stepan Kochemazov. Improving implementation of SAT competitions 2017–2019 winners. In Proceedings of SAT 2020, LNCS 12178, pages 139–148, 2020. 23 Miyuki Koshimura, Tong Zhang, Hiroshi Fujita, and Ryuzo Hasegawa. QMaxSAT: A Partial Max-SAT solver. J. Satisf. Boolean Model. Comput., 8(1/2):95–100, 2012. 24 Adrian Kuegel. Improved exact solver for the Weighted MAX-SAT problem. In Proceedings of Workshop Pragmatics of SAT, POS-10, Edinburgh, UK, pages 15–27, 2010. 25 Zhendong Lei and Shaowei Cai. Solving (Weighted) Partial MaxSAT by dynamic local search for SAT. In Proceedings of IJCAI 2018, pages 1346–1352, 2018. 26 Chu Min Li and Felip Manyà. MaxSAT, hard and soft constraints. In Handbook of satisfiability, second edition, pages 903–927. IOS Press, 2021. 27 Chu Min Li, Felip Manya, Nouredine Ould Mohamedou, and Jordi Planes. Resolution-based lower bounds in MaxSAT. Constraints, 15(4):456–484, 2010.   28 Chu Min Li, Felip Manya, and Jordi Planes. Exploiting unit propagation to compute lower bounds in branch and bound Max-SAT solvers. In Proceedings of CP 2005, pages 403–414. Springer, 2005. 29 Chu Min Li, Felip Manya, and Jordi Planes. Detecting disjoint inconsistent subformulas for computing lower bounds for Max-SAT. In Proceedings of AAAI 2006, pages 86–91, 2006. 30 Chu Min Li, Felip Manyà, and Jordi Planes. New inference rules for Max-SAT. Journal of Artificial Intelligence Research, 30:321–359, 2007. 31 Chu-Min Li, Fan Xiao, Mao Luo, Felip Manyà, Zhipeng Lü, and Yu Li. Clause vivification by unit propagation in CDCL SAT solvers. Artificial Intelligence, 279, 2020. 32 Jia Hui Liang, Chanseok Oh, Vijay Ganesh, Krzysztof Czarnecki, and Pascal Poupart. Maple- COMSPS, MapleCOMSPS LRB, MapleCOMSPS CHB. In Proceedings of SAT Competition 2016: Solver and Benchmark Descriptions, pages 52–53, 2016. 33 Michael Luby, Alistair Sinclair, and David Zuckerman. Optimal speedup of Las Vegas algorithms. Information Processing Letters, 47(4):173–180, 1993. 34 Mao Luo, Chu-Min Li, Fan Xiao, Felip Manyà, and Zhipeng Lü. An effective learnt clause minimization approach for CDCL SAT solvers. In Proceedings of IJCAI 2017, pages 703–711, 2017. 35 Vasco M. Manquinho, Joao Marques-Silva, and Jordi Planes. Algorithms for weighted Boolean optimization. In Proceedings of SAT 2009, pages 495–508. Springer LNCS 5584, 2009. 36 Joao Marques-Silva and Vasco M. Manquinho. Towards more effective unsatisfiability-based maximum satisfiability algorithms. In Proceedings of SAT 2008, pages 225–230. Springer LNCS 4996, 2008. 37 Ruben Martins, Vasco M. Manquinho, and Inês Lynce. Open-WBO: A modular MaxSAT solver. In Proceedings of SAT 2014, volume 8561 of LNCS, pages 438–445. Springer, 2014. 38 Matthew W. Moskewicz, Conor F. Madigan, Ying Zhao, Lintao Zhang, and Sharad Malik. Chaff: Engineering an efficient SAT solver. In Proceedings of DAC 2001, pages 530–535. ACM, 2001. 39 Nina Narodytska and Fahiem Bacchus. Maximum satisfiability using core-guided MaxSAT resolution. In Proceedings of AAAI 2014, pages 2717–2723, 2014. 40 Tobias Paxian and Bernd Becker. Pacose: An iterative SAT-based MaxSAT solver. In MaxSAT Evaluation 2020: Solver and Benchmark Descriptions, page 12, 2020. 41 Paul Saikko, Jeremias Berg, and Matti Järvisalo. LMHS: A SAT-IP hybrid MaxSAT solver. In Proceedings of SAT 2016, volume 9710 of LNCS, pages 539–546, 2016. 42 Carsten Sinz. Towards an optimal CNF encoding of Boolean cardinality constraints. In Proceedings of CP 2005, pages 827–831. Springer LNCS 3709, 2005. 43 Fulya Trösser, Simon De Givry, and George Katsirelos. Relaxation-aware heuristics for exact optimization in graphical models. In Prodeedings of CPAIOR 2020, pages 475–491. Springer, 2020. 44 Aolong Zha. QMaxSAT in MaxSAT Evaluation 2018. In Proceedings of the MaxSAT Evaluation 2020, page 16, 2020.