文献学习--Deep Cooperation of CDCL and Local Search for SAT

Deep Cooperation of CDCL and Local Search for SAT

Cai S., Zhang X. (2021) Deep Cooperation of CDCL and Local Search for SAT. In: Li CM., Manyà F. (eds) Theory and Applications of Satisfiability Testing – SAT 2021. SAT 2021. Lecture Notes in Computer Science, vol 12831. Springer, Cham. https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-030-80223-3_6

Abstract

 

Modern SAT solvers are based on a paradigm named conflict driven clause learning (CDCL), while local search is an important alternative. Although there have been attempts combining these two methods, this work proposes deeper cooperation techniques. 译文：尽管有人尝试将这两种方法结合起来，但这项工作提出了更深层次的合作技术。

First, we relax the CDCL framework by extending promising branches to complete assignments and calling a local search solver to search for a model nearby. 译文：首先，我们通过扩展有希望的分支来完成任务，并调用局部搜索求解器来搜索附近的模型来放松CDCL框架。

More importantly, the local search assignments and the conflict frequency of variables in local search are exploited in the phase selection and branching heuristics of CDCL. 译文：更重要的是，在CDCL的相位选择和分支启发式中，利用了局部搜索分配和局部搜索变量的冲突频率。

We use our techniques to improve three typical CDCL solvers (glucose, MapleLCMDistChronoBT and Kissat). Experiments on benchmarks from the Main tracks of SAT Competitions 2017–2020 and a real world benchmark of spectrum allocation show that the techniques bring significant improvements, particularly on satisfiable instances.译文：这些技术带来了显著的改进，特别是在SAT的实例上。

For example, the integration of our techniques allow the three CDCL solvers to solve 62, 67 and 10 more instances in the benchmark of SAT Competition 2020. A resulting solver won the Main Track SAT category in SAT Competition 2020 and also performs very well on the spectrum allocation benchmark.

As far as we know, this is the first work that meets the standard of the challenge “Demonstrate the successful combination of stochastic search and systematic search techniques, by the creation of a new algorithm that outperforms the best previous examples of both approaches.” [35] on standard application benchmarks.
   

1 Introduction

  SAT solvers are often used as a core component of more complex tools such as solvers for Satisfiability Module Theory (SMT), which are indispensable for program analysis and software verification. 译文：SAT求解器通常作为更复杂工具的核心组件，如满足性模块理论(SMT)求解器，在程序分析和软件验证中是必不可少的。
   
   CDCL is evolved from the DPLL backtracking procedure [14], and usually involves a number of key techniques, mainly including 1) clause learning from conflicts [36], 2) exploiting the structure of conflicts during clause learning [36], 3) learnt clause management scheme [4], 4) lazy data structures for the representation of formulas [31], 5) effective branching heuristics, e.g., VSIDS [31], and 6) periodically restarting [18]. Additional techniques used in recent CDCL solvers include phase saving [34], switching between “stabilizing” mode (seldom-restart) and frequent-restart mode [33], clause veriification [29], among others.
   
 

There have been attempts combining CDCL and local search solvers. However, in previous hybrid solvers, CDCL and local search solvers usually see each other as a black box and the hybrid solver invokes the respective solver according to different situations [3, 5, 19, 24, 30].

译文：有人尝试将CDCL和本地搜索解决方案结合起来。然而，在以往的混合求解器中，CDCL和局部搜索求解器通常将对方视为一个黑盒子，混合求解器根据不同的情况调用各自的求解器[3,5,19,24,30]。
 

This work is devoted to deeper cooperation of CDCL and local search for SAT, where CDCL is the main solver and local search is used as an aiding tool. 译文：本工作致力于CDCL与SAT的本地搜索的深入合作，其中CDCL是主要的解决方案，本地搜索作为辅助工具。

We propose three ideas to use local search to help CDCL in different ways. 译文：我们提出了三种使用本地搜索以不同方式帮助CDCL的想法。

The first idea is a method for plugging a local search solver into a CDCL solver, while the other two ideas concern with using information produced by the local search solver to enhance CDCL. We summarize the three techniques below.
 

Explore promising branches by local search (Sect. 3)

The first idea is to a novel method to plug a local search solver into a CDCL solver. We relax the backtrack process by allowing some promising branches to be extended to a complete assignment without backtracking, even if conflicts are met during extending the assignment. Then, a local search solver is called to find a model nearby. If the local search cannot find a model within a given time limit, the CDCL search process continues as normal from the node where the algorithm enters the non-backtracking phase.
 

Phase selection with local search assignments (Sect. 4)

Phase selection refers to pick a truth value (usually called phase) to assign the branching variable. Most modern CDCL solvers implement a phase selection heuristic named phase saving [34], which keeps the branching phase and uses the saved phase when a variable is picked to branch. Recent progress shows that using some other forms of target phase, e.g., the value under the largest conflict-free assignment in the solver, random value and the opposite of the saved phase, to reset the saved phase periodically could be beneficial [10]. We propose a phase resetting technique, which mainly relies on the assignments produced by the integrated local search solver.
 

Branching with local search conflict information (Sect. 5)

We use the variables’ conflict frequency, i.e., the frequency appearing in unsatisfied clauses during local search, to enhance the branching heuristic in CDCL. Specifically, such information is used to modify the variables’ activity in VSIDS heuristic and the variables’ learning rate in LRB heuristic.
   
  We apply our techniques to three state-of-the-art CDCL solvers, including the latest version of glucose [4], and the winner of the Main track of SAT Competition 2019 and 2020 namely MapleLCMDistChronoBT-DL [22] and Kissat_sat [10]. The experimental results show that our techniques allow them to solve a remarkable number of additional instances in the main track benchmark of SAT Competition 2017–2020. For example, the integration of our techniques allow the three CDCL solvers to solve 62, 67 and 10 more instances in the benchmark of SAT Competition 2020. Besides, the improved version of the three CDCL solvers also shows better results on a real world benchmark arising from a spectrum repacking problem in the context of bandwidth auction.
   
  Seen from experiments, the promising branches exploration technique and the local search based phase resetting techniques are very helpful to solve satisfiable instances, with a price of slight degradation on unsatisfiable instances (usually solving 2 or 3 fewer unsatisfiable instances). The local search conflict frequency enhanced branching strategy can be positive to satisfiable and also saves back a few unsatisfiable instances. Overall, these techniques significantly improves the performance of the CDCL solvers, leading to a remarkable increase on the number of total solved instances.
   

2 Preliminaries

 

2.1 Preliminary Definitions and Notations
  。。。
   
 

2.2 CDCL Solvers
   
 

2.3 Local Search Solvers
  For local search algorithms, we need to define the search space and a neighborhood relation. In the context of SAT, the search space is the set of complete assignments which can be characterized as the set of strings {0,1}n{0,1}n, where n is the number of variables in the formula. For SAT, the seemingly most natural neighborhood N maps candidate solutions to their set of Hamming neighbors, i.e., candidate solutions that differ in exactly one variable. A local search algorithm starts from a position of search space and then moves to one neighbor of the current position in each step, trying to find a position which represents a satisfying assignment.
   
 

2.4 Experiment Preliminaries
  In this work, we use our methods to improve CDCL solvers and carry out extensive experiments to evaluate the effectiveness of the methods. In this subsection, we introduce the experiment setup including base solvers, benchmarks, running environment and reporting methodology. 译文：在这项工作中，我们使用我们的方法来改进CDCL求解器，并进行广泛的实验来评估方法的有效性。在本小节中，我们将介绍实验设置，包括基本求解器、基准、运行环境和报告方法
   。。。
 

 Experiment Setup: 

All experiments were conducted on a cluster of computers with Intel Xeon Platinum 8153 @2.00GHz CPUs and 1024G RAM under the operating system CentOS 7.7.1908.

For each instance, each solver was performed one run, with a cutoff time of 5000 CPU seconds.

For each solver for each benchmark, we report the number of solved SAT/UNSAT instances and total solved instances, denoted as ‘#SAT’, ‘#UNSAT’ and ‘#Solved’, and the penalized run time ‘PAR2’ (as used in SAT Competitions), where the run time of a failed run is penalized as twice the cutoff time. 译文：运行失败的运行时间被罚为截止时间的两倍。
   

 

3 Exploring Promising Branches by Local Search

 

In this section, we present our method for plugging a local search solver into a CDCL solver. The method helps finding a model faster, by exploring promising branches via local search.

译文：在本节中，我们将介绍将本地搜索求解器插入到CDCL求解器中的方法。该方法通过局部搜索来探索有希望的分支，有助于更快地找到模型。
   
 

First, we provide the motivation of our method.

By using reasoning techniques, CDCL solvers are able to prune most of the branches of the search tree. This is useful for solving unsatisfiable instances—to prove a formula is unsatisfiable, a CDCL solver needs to examine the whole search space, and therefore the more of the search tree is pruned, the more efficient the solver is. 译文：这对于解决不可满足的实例是有用的——为了证明一个公式是不可满足的，CDCL求解器需要检查整个搜索空间，因此搜索树被修剪得越多，求解器的效率就越高。

However, when solving satisfiable formulas, some promising branches that are close to a satisfying assignment are also pruned without any exploitation. This would make CDCL solvers miss some opportunities of finding a solution. In our opinion, the exploration on promising branches may improve CDCL solvers on satisfiable formulas, and a natural way to do so is to employ local search at such branches. 
 

 

 

 

 

放松CDCL的总体程序
 

Now, we present a method to explore promising branches during the search procedure of CDCL solvers, which can improve the ability to find solutions while keeping the completeness of the solvers. For this method, we need to identify which branches (i.e., partial assignments) deserve exploration. 译文：对于这个方法，我们需要确定哪些分支(即部分分配)值得探索。

We propose two conditions below, and any assignment α satisfying at least one of them is considered as promising and will be explored:
   

 
 

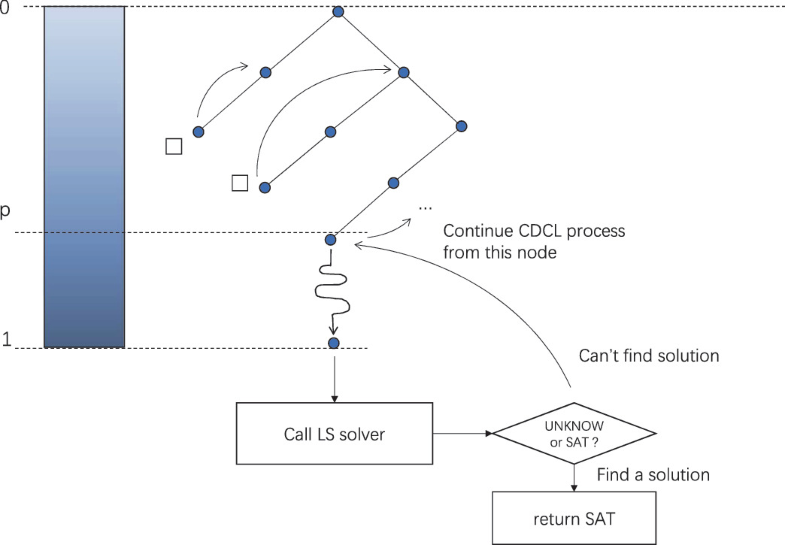
With the conditions of promising assignments, the method is described as follows (depicted in Fig. 1).

 

During the search of CDCL, whenever reaching a node corresponding to a promising assignment, the algorithm enters a non-backtracking mode, which uses unit propagation and heuristics in CDCL to assign the remaining variables without backtracking, even an empty clause is detected. At the end, this leads to a complete assignment ββ, which is fed to a local search solver to search for a model nearby. If the local search fails to find a model within a certain time budget, then the algorithm goes back to the normal CDCL search from the node where it was interrupted (we call this a breakpoint). The non-backtracking phase does not change the data structures used for CDCL search process. In this work, each call of the local search solver is cutoff when reaching a certain amount of memory accesses (5×1075×107).
   

4 Phase Resetting with Local Search Assignments

  In Sect. 3, we propose a method to plug a local search solver into boost CDCL solvers. Now, we propose a phase resetting heuristic based on the assignments obtained by the local search processes. 译文：我们提出了一种基于局部搜索过程所获得的分配的阶段重置启发式算法。
   
 

Phase selection is an important component of a CDCL solver. Most modern CDCL solvers utilize the phase saving heuristic [34], which returns the phase of a variable x corresponding to the last time x was assigned.

This caching scheme reduces the repetition caused by non-chronological backtracking. Recently, Biere et al. proposed a phase resetting technique which overwrites all saved phases with some other information, based on the interval of number of conflicts encountered, which gives another boost to the performance [10].
   
 

 

 
  Algorithm 2 describes a CDCL solver that implements the idea of exploring promising branches and phase resetting technique. After each time the CDCL solver is restarted, the technique overwrites the saved phases of all variables with assignments produced by local search. To this end, we record the best assignment (with the fewest unsatisfied clauses) in each run of the local search solver, and when we say the assignment of a local search procedure (run), we refer to the best assignment in this procedure.
   
  For our phase resetting technique, we consider the following assignments, all of which come from the assignments of the local search procedures.
 
  It is easy to see that α_max_LSα_max_LS and α_best_LSα_best_LS serve for the aim to maximize the depth of the branch, while α_latest_LSα_latest_LS adds diversification in some sense, as different local search procedures start with initial assignments built upon different branches. Overall, it is expected this phase resetting technique with local search assignments would work well particularly for satisfiable instances, and our experiment results confirm this.
   
  Phase Resetting Based on Local Search Assignment: Whenever the CDCL is restarted, we overwrites the saved phases. For each variable x, its phase is set according to the following probability distribution (Table 1).
 

 
   

5 Branching with Conflict Frequency in Local Search

 

CDCL is a powerful framework owing largely to the utilization of the conflict information, and branching strategies aim to promote conflicts. In this section, we use a variable property which we refer to as conflict frequency in local search to improve the branching strategy of CDCL. 译文：在本节中，我们使用一个变量属性，即局部搜索中的冲突频率，来改进CDCL的分支策略。
   
 

The best known branching strategy is VSIDS (Variable State Independent Decaying Sum) [31], which is surprisingly effective and also works well with restarts.

Although variants [7, 8, 15, 16, 17] have been proposed over the years, they are similar in spirit to VSIDS in the sense that they prefer to pick variables participating in recent conflicts. 译文：尽管变体[7,8,15,16,17]已经提出多年，但它们在精神上与VSIDS相似，因为它们更喜欢选择参与最近冲突的变量。

Briefly speaking, the VSIDS heuristic maintains an activity score for each variable, and prefers to pick the variable with the maximum activity score. The activity score of a variable reflects the frequency that it occurs in conflicts, with emphasis on those in the recent period (please refer to [31] and [15] for more details).
   
 

Recently, a new branching strategy LRB (the learning rate based branching heuristic) [27] shows its effectiveness in the Maple series, which regularly won gold medals in main track of SAT Competitions since 2016.

LRB is based on the concept called learning rate, which measures the portion of learnt clauses involving the variable among all learnt clauses in the period between the assignment of x until it transitions back to being unassigned (please refer to [27] for more details). 译文：LRB是基于学习率的概念，它衡量的是在赋值x到未赋值x之间的时间段内，包含该变量的已学习子句在所有已学习子句中的比例(详情请参阅[27])。
   
 

Intuitively, both VSIDS and LRB prefer to pick variables with higher frequencies occurring in conflicts, with an emphasis in a recent period. 译文：直观上，VSIDS和LRB都倾向于选择冲突中发生频率较高的变量，重点是最近的时期。

We propose to enhance the branching strategy by utilizing the conflict frequency of variables in the latest local search procedure. 译文：我们提出在最新的局部搜索过程中利用变量的冲突频率来增强分支策略。
   

 
   
   
   
   
   
   
   
   
   
   
   
   

 

6 Experiments

 

We carry out extensive experiments to evaluate the effectiveness of our methods.

The experiment setup is described in Sect. 2.4. For glucose and MapleLCMDistChronoBT-DL-v2.1, we implement all the three techniques in this work, including relaxed CDCL with local search (denoted as rx), phase resetting with local search (denoted as rp) and local search conflict frequency enhanced branching (denoted as cf). For Kissat_sat, we only implement the cf technique, as it is challenging to implement the relaxed CDCL framework in it, due to the difficulty of identifying all current clauses (which should be provided to local search) in the Kissat_sat solver. Nevertheless, it is easy to apply the cf technique to Kissat, which is what we do in this work. All the source codes, origin experiment statistics and the detailed data for Table 2 can be downloaded online.5
  。。。
  We can see that the local search solver returns a solution for some instances, and this number varies considerably with the benchmarks. A natural question is: Whether the improvements come mainly from the complementation of CDCL and local search solvers that they solve different instances? If this were true, then a simple portfolio that runs both CDCL and local search solvers would work similarly to the hybrid solvers in this work. To answer this question, we compare the instances solved by the hybrid solvers with those by the base CDCL solver and the local search solver (both the CDCL and local search solver are given 5000 s for each instance). We observe that, there is a large number of instances (denoted by #SAT_bonus) that both CDCL and local search solvers fail to solve but can be solved by the hybrid solvers. For these instances, even a virtual best solver that picks the solver with the best result for each instance would fail. For glucose, this number reaches 29, 36, 26 and 37 for the four benchmarks respectively, while for MapleLCMDIstChronoBT-DL, this number reaches 16, 18, 15 and 36 respectively. This indicates the cooperation techniques have essential contributions to the good performance of the hybrid solvers.
   
  We also calculate the number of calls of the local search solver in each run. This figure is usually from 10 to 25 for these benchmarks. As for the run time of local search, which can be seen as the price paid for the benefit of using local search, we calculate the portion of the time spent on local search. This figure is between 6% and 20% for the satisfiable instances, and it drops significantly on unsatisfiable instances, which is usually less than 7%. This is not inconsistent with the observations that the number of local search calls is not necessarily fewer on unsatisfiable instances, because the portion of the time on local search also depends on the total time of the hybrid solver. Our statistics show that the averaged time on solving UNSAT instances is about 1.5×1.5× to 2×2× that on SAT instances for both glucose+rx+rp+cf and Maple-DL+rx+rp+cf. In a nutshell, the price is acceptable and usually small for the UNSAT instances, which also partly explains that our techniques do not have obvious negative impact on solving UNSAT instances although they incline to the satisfiable side.
   

7 Related Works

  There has been interest in combining systemic search and local search for solving SAT. Indeed, it was pointed as a challenge by Selman et al. [35]. Previous attempts can be categorized into two families according to the type (DPLL/CDCL or local search) of the main body solver.
   
  A family of hybrid solvers use a local search solver as the main body solver. An incomplete hybrid solver hybridGM [5] calls CDCL search around local minima with only one unsatisfied clause. Audemard et al. proposed a hybrid solver named SATHYS [2, 3]. Each time the local search solver reaches a local minimum, a CDCL solver is launched. Some reasoning techniques or information from CDCL solvers have been used to improve local search solvers. Resolution techniques were integrated to local search solvers [1, 13]. Recently, Lorenz and Wörz developed a hybrid solver GapSAT [28], which used a CDCL solver as a preprocessor before running the local search solver ProbSAT. The experiments showed that, the learnt clauses produced by CDCL solver were useful to improve the local search solver on random instances.
   
  The other family of hybrid solvers focus on boosting CDCL solvers by local search, and this work belongs to this line. A simple way for hybridizing local search and CDCL is to call local search before CDCL begins, trying to solve the instance or derive information such as variable ordering to be used in CDCL. The hyrid solvers Sparrow2Riss [6], CCAnr+glucose [11] and SGSeq [25] belong to this family.
   
  Some works use local search to find a subformula for CDCL to solve. In [30], a local search solver is used to find a part of the formula which is satisfiable, which helps to divide the formula into two parts for the DPLL solver. In HINOTOS [24], a local search is used to identify a subset of clauses to be passed to a CDCL solver in an incremental way.
   
  The most related works belong to those that call a local search solver during the CDCL procedure. WalkSatz [19] calls a local search solver WalkSAT at each node of a DPLL solver Satz. However, this is time consuming. This can be done in parallel with shared memory [23]. In CaDiCaL and Kissat [10], a local search solver is called when the solver resets the saved phases, and the phases produced by local search are used only once immediately after the local search process. However, the way CaDiCaL and Kissat use the local search assignments is different from our phase resetting method based on local search. CaDiCaL and Kissat only record the current local search assignment, which is used just for once right after the local search exists. They do not use information of previous local search processes. In fact, we also carry out experiments to see the impact of local search on the performance of Kissat_sat, which turns out to be limited. When Kissat_sat works without local search, #SAT drops by 5 on average over the SC benchmarks.
   
  Although previous attempts have been made trying to combine the strength of CDCL and local search, they did not lead to hybrid solvers essentially better than CDCL solvers on application instances. This work, for the first, meets the standard of the challenge “create a new algorithm that outperforms the best previous examples of both approaches” [35] on standard application benchmarks from SAT Competitions.
   

8 Conclusions

  This work took a large step towards deep cooperation of CDCL and local search. We proposed three techniques for using local search to improve CDCL solvers. The first idea is to protect promising branches from being pruned, and exploit them using a local search solver. The second idea is to utilize the assignments of the local search processes to reset the saved phases in the phase selection heuristic. Finally, we proposed to enhance the branching strategy of CDCL solvers by considering the conflict frequency of variables in the local search process. These techniques significantly improve the performance of state of the art CDCL solvers on application benchmarks. The proposed methods are generic and can be applied to improve other CDCL solvers.
   
  This is the first time that the combination of stochastic search and systematic search techniques leads to essential improvements over the state of the art of both approaches on application benchmarks, thus answering Challenge 7 of the Ten Challenges in Propositional Reasoning and Search [35].
   

 

 

 

Footnotes

  1. 1.
  2. 2.
  3. 3.
  4. 4.
  5. 5.
  6. 6.

References

 
  1. 1.
    Anbulagan, Pham, D.N., Slaney, J.K., Sattar, A.: Old resolution meets modern SLS. In: Proceedings of AAAI 2005, pp. 354–359 (2005)Google Scholar
  2. 2.
    Audemard, G., Lagniez, J., Mazure, B., Sais, L.: Integrating conflict driven clause learning to local search. In: Proceedings of LSCS 2009, pp. 55–68 (2009)Google Scholar
  3. 3.
    Audemard, G., Lagniez, J.-M., Mazure, B., Saïs, L.: Boosting local search thanks to cdcl. In: Fermüller, C.G., Voronkov, A. (eds.) LPAR 2010. LNCS, vol. 6397, pp. 474–488. Springer, Heidelberg (2010).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-642-16242-8_34CrossRefGoogle Scholar
  4. 4.
    Audemard, G., Simon, L.: Predicting learnt clauses quality in modern SAT solvers. In: Proceedings of IJCAI 2009, pp. 399–404 (2009)Google Scholar
  5. 5.
    Balint, A., Henn, M., Gableske, O.: A novel approach to combine a SLS- and a DPLL-solver for the satisfiability problem. In: Kullmann, O. (ed.) SAT 2009. LNCS, vol. 5584, pp. 284–297. Springer, Heidelberg (2009).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-642-02777-2_28CrossRefGoogle Scholar
  6. 6.
    Balint, A., Manthey, N.: SparrowToRiss 2018. In: Proceedings of SAT Competition 2018: Solver and Benchmark Descriptions, pp. 38–39 (2018)Google Scholar
  7. 7.
    Biere, A.: Adaptive restart strategies for conflict driven SAT solvers. In: Kleine Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 28–33. Springer, Heidelberg (2008).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-540-79719-7_4CrossRefzbMATHGoogle Scholar
  8. 8.
    Biere, A.: Pre, icosat@sc’09. In: SAT 2009 Competitive Event Booklet, pp. 42–43 (2009)Google Scholar
  9. 9.
    Biere, A.: Yet another local search solver and lingeling and friends entering the sat competition 2014. Sat Competition 2014(2), 65 (2014)Google Scholar
  10. 10.
    Biere, A., Fazekas, K., Fleury, M., Heisinger, M.: CaDiCaL, Paracooba, Plingeling and Treengeling entering the SAT Competition, Kissat, pp. 51–53 (2020)Google Scholar
  11. 11.
    Cai, S., Luo, C., Su, K.: CCAnr+glucose in SAT Competition 2014. In: Proceedings of SAT Competition 2014: Solver and Benchmark Descriptions, p. 17 (2014)Google Scholar
  12. 12.
    Cai, S., Luo, C., Su, K.: CCAnr: a configuration checking based local search solver for non-random satisfiability. In: Proceedings of SAT 2015, pp. 1–8 (2015)Google Scholar
  13. 13.
    Cha, B., Iwama, K.: Adding new clauses for faster local search. In: Proceedings of AAAI, vol. 96, pp. 332–337 (1996)Google Scholar
  14. 14.
    Davis, M., Logemann, G., Loveland, D.W.: A machine program for theorem-proving. Commun. ACM 5(7), 394–397 (1962)MathSciNetCrossRefGoogle Scholar
  15. 15.
    Eén, N., Sörensson, N.: An extensible SAT-solver. In: Giunchiglia, E., Tacchella, A. (eds.) SAT 2003. LNCS, vol. 2919, pp. 502–518. Springer, Heidelberg (2004).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-540-24605-3_37CrossRefGoogle Scholar
  16. 16.
    Gershman, R., Strichman, O.: Haifasat: a new robust SAT solver. In: Ur, S., Bin, E., Wolfsthal, Y. (eds.) Proceedings of Haifa Verification Conference 2005, pp. 76–89 (2005)Google Scholar
  17. 17.
    Goldberg, E.I., Novikov, Y.: Berkmin: a fast and robust sat-solver. In: Proceedings of DATE (2002), pp. 142–149 (2002)Google Scholar
  18. 18.
    Gomes, C.P., Selman, B., Kautz, H.A.: Boosting combinatorial search through randomization. In: Proceedings of AAAI/IAAI 1998, pp. 431–437 (1998)Google Scholar
  19. 19.
    Habet, D., Li, C.M., Devendeville, L., Vasquez, M.: A hybrid approach for SAT. In: Proceedings of CP 2002, pp. 172–184 (2002)Google Scholar
  20. 20.
    Heule, M.J.H., Kullmann, O., Marek, V.W.: Solving and verifying the boolean pythagorean triples problem via cube-and-conquer. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 228–245. Springer, Cham (2016).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-40970-2_15CrossRefzbMATHGoogle Scholar
  21. 21.
    Kautz, H.A., Selman, B.: Planning as satisfiability. In: Proceedings of ECAI 1992, pp. 359–363 (1992)Google Scholar
  22. 22.
    Kochemazov, S., Zaikin, O., Kondratiev, V., Semenov, A.: Maplelcmdistchronobt-dl, duplicate learnts heuristic-aided solvers at the sat race 2019. In: Proceedings of SAT Race, pp. 24–24 (2019)Google Scholar
  23. 23.
    Kroc, L., Sabharwal, A., Gomes, C.P., Selman, B.: Integrating systematic and local search paradigms: a new strategy for maxsat. In: Proceedings of IJCAI 2009, pp. 544–551 (2009)Google Scholar
  24. 24.
    Letombe, F., Marques-Silva, J.: Improvements to hybrid incremental SAT algorithms. In: Kleine Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 168–181. Springer, Heidelberg (2008).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-540-79719-7_17CrossRefzbMATHGoogle Scholar
  25. 25.
    Li, C.M., Habet, D.: Description of RSeq2014. In: Proceedings of SAT Competition 2014: Solver and Benchmark Descriptions, p. 72 (2014)Google Scholar
  26. 26.
    Li, C.M., Li, Yu.: Satisfying versus falsifying in local search for satisfiability. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 477–478. Springer, Heidelberg (2012).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-642-31612-8_43CrossRefGoogle Scholar
  27. 27.
    Liang, J.H., Ganesh, V., Poupart, P., Czarnecki, K.: Learning rate based branching heuristic for SAT solvers. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 123–140. Springer, Cham (2016).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-40970-2_9CrossRefzbMATHGoogle Scholar
  28. 28.
    Lorenz, J.-H., Wörz, F.: On the effect of learned clauses on stochastic local search. In: Pulina, L., Seidl, M. (eds.) SAT 2020. LNCS, vol. 12178, pp. 89–106. Springer, Cham (2020).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-030-51825-7_7CrossRefzbMATHGoogle Scholar
  29. 29.
    Luo, M., Li, C., Xiao, F., Manyà, F., Lü, Z.: An effective learnt clause minimization approach for CDCL SAT solvers. In: Proceedings of IJCAI 2017, pp. 703–711 (2017)Google Scholar
  30. 30.
    Mazure, B., Sais, L., Grégoire, É.: Boosting complete techniques thanks to local search methods. Ann. Math. Artif. Intell. 22(3–4), 319–331 (1998)MathSciNetCrossRefGoogle Scholar
  31. 31.
    Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: engineering an efficient SAT solver. In: Proceedings of the 38th Design Automation Conference, DAC 2001, pp. 530–535 (2001)Google Scholar
  32. 32.
    Newman, N., Fréchette, A., Leyton-Brown, K.: Deep optimization for spectrum repacking. Commun. ACM 61(1), 97–104 (2018)CrossRefGoogle Scholar
  33. 33.
    Oh, C.: Between SAT and UNSAT: the fundamental difference in CDCL SAT. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 307–323. Springer, Cham (2015).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-319-24318-4_23CrossRefGoogle Scholar
  34. 34.
    Pipatsrisawat, K., Darwiche, A.: A lightweight component caching scheme for satisfiability solvers. In: Marques-Silva, J., Sakallah, K.A. (eds.) SAT 2007. LNCS, vol. 4501, pp. 294–299. Springer, Heidelberg (2007).  https://doi-org-s.era.lib.swjtu.edu.cn/10.1007/978-3-540-72788-0_28CrossRefGoogle Scholar
  35. 35.
    Selman, B., Kautz, H.A., McAllester, D.A.: Ten challenges in propositional reasoning and search. In: Proceedings of IJCAI, vol. 97, pp. 50–54 (1997)Google Scholar
  36. 36.
    Silva, J.P.M., Sakallah, K.A.: GRASP - a new search algorithm for satisfiability. In: Proceedings of ICCAD 1996, pp. 220–227 (1996)Google Scholar
  37. 37.
    Silva, J.P.M., Sakallah, K.A.: Boolean satisfiability in electronic design automation. In: Proceedings of the DAC 2000, pp. 675–680 (2000)Google Scholar
   
posted on 2021-11-06 17:22  海阔凭鱼跃越  阅读(282)  评论(0)  编辑  收藏  举报