Efficient All-UIP Learned Clause Minimization
Mathias Fleury and Armin Biere Johannes Kepler University, Linz, Austria {armin.biere, mathias.fleury}@jku.at
重要技术要点:
[8]版本通过计算冲突子句每一层的唯一隐含点(UIP)来缩短学习子句,限制在较低的层次上不添加文字。
Abstract
| Abstract. In 2020 Feng & Bacchus revisited variants of the all-UIP learning strategy, which considerably improved performance of their version of CaDiCaL submitted to the SAT Competition 2020, particularly on large planning instances. We improve on their algorithm by tightly integrating this idea with learned clause minimization. This yields a clean shrinking algorithm with complexity linear in the size of the implication graph. It is fast enough to unconditionally shrink learned clauses until completion. We further define trail redundancy and show that our version of shrinking removes all redundant literals. Independent experiments with the three SAT solvers CaDiCaL, Kissat, and Satch confirm the effectiveness of our approach. | |
1 Introduction
|
Learned clause minimization [18] is a standard feature in modern SAT solvers. It allows to learn shorter clauses which not only reduces memory usage but arguably also helps to prune the search space.译文:它允许学习更短的子句,这不仅减少内存使用,而且可以帮助削减搜索空间。 However, completeness of minimization was never formalized nor proven. Using Horn SAT [9] we define trail redundancy through entailment with respect to the reasons in the trail and show that the standard minimization algorithm removes all redundant literals (Sect. 2). 译文:然而,最小化的完整性从来没有被形式化或证明过。使用Horn SAT[9],我们根据轨迹中的原因通过蕴涵定义了轨迹冗余,并证明了标准最小化算法消除了所有冗余文字(第2节)。 |
|
|
Minimization, in its original form [18], only removes literals from the initial deduced clause during conflict analysis, i.e., the 1st-unique-implication-point clause [21]. In 2020 Feng & Bacchus [11] revisited the all-UIP heuristics with the goal to reduce the size of the deduced clause even further by allowing to add new literals. 译文:2020年,Feng & Bacchus[11]重新审视了全uip启发式,目标是通过允许添加新的字面量来进一步减少推导出的子句的大小。
In this paper we call such advanced minimization techniques shrinking. In order to avoid spending too much time in such shrinking procedures the authors of [11] had to limit its effectiveness. They also described and implemented several variants in the SAT solver CaDiCaL [2]. One variant was winning the planning track of the SAT Competition 2020. The benchmarks in this track require to learn clauses with many literals on each decision level. 译文:在本文中,我们称这种先进的极小化技术为收缩。为了避免在这种收缩过程中花费太多的时间,[11]的作者不得不限制其有效性。他们还描述和实现了SAT求解器CaDiCaL[2]中的几个变体。其中一个变化是赢得了2020年SAT竞赛的规划轨道。本课程的基准要求学习在每个决策级别上具有许多字面量的子句。 |
|
|
As Feng & Bacchus [11] consider minimization and all-UIP shrinking separately, they apply minimization first, then all-UIP shrinking, and finally again minimization (depending on the deployed strategy/variant), while we integrate both techniques into one simple algorithm. 译文:由于Feng和Bacchus[11]分别考虑最小化和全uip收缩,他们首先应用最小化,然后全uip收缩,最后再次最小化(取决于部署的策略/变量),而我们将这两种技术集成到一个简单的算法中。 In contrast, their variants process literals of the deduced clause from highest to lowest decision level and eagerly introduce literals on lower levels. Thus their approach has to be guarded against actually producing larger clauses and can not be run unconditionally (Sect. 3). 译文:相反,它们的变体将推导子句的字面量从最高决策层处理到最低决策层,并急切地在较低的决策层引入字面量。因此,他们的方法必须防止实际产生更大的条款,不能无条件地运行(第3节)。 |
|
|
We integrate minimization and shrinking in one procedure with linear complexity in the size of the implication graph (Sect. 4). Processing literals of the deduced clause from lowest to highest level allows us to reuse the minimization cache, without compromising on completeness, thus making it possible to run the shrinking algorithm unconditionally until completion. On the theoretical side we prove that our form of shrinking fulfills the trail redundancy criteria。 译文:我们将最小化和收缩集成到一个过程中,该过程具有隐含图大小的线性复杂性(第4节)。从最低层到最高层处理推导子句的字面量允许我们重用最小化缓存,而不损害完整性,这样就可以无条件地运行收缩算法直到完成。在理论方面,我们证明了我们的收缩形式满足trail冗余准则。 |
|
| Experiments with our SAT solvers Kissat, CaDiCaL, and Satch show the effectiveness of our approach and all-UIP shrinking in general. Shrinking decreases the number of learned literals, particularly on the recent planning track. We also study the amount of time used by the different parts of the transformation from a conflicting clause to the shrunken learned clause (Sect. 5).译文:用我们的SAT求解器Kissat、CaDiCaL和Satch进行的实验显示了我们方法的有效性和总体上的全uip收缩。收缩减少了学习文字的数量,特别是在最近的计划轨道上。我们还研究了从冲突条款到缩减的学习条款的不同部分所使用的时间(第5节)。 | |
|
Regarding related work we refer to the Handbook of Satisfiability [7], particularly for an introduction to CDCL [17], the main algorithm used by state-of-theart SAT solvers. This work is based on the classical minimization algorithm [18], which Van Gelder [19] improved by making it linear (in the number of literals) in the implication graph without changing the resulting minimized clause. 译文:关于相关工作,我们参考了《满足手册[7]》,特别是对CDCL[17]的介绍,这是目前最先进的SAT求解器使用的主要算法。本文基于经典的最小化算法[18],Van Gelder[19]对该算法进行了改进,使其在蕴涵图中线性化(字面量的数量),而不改变得到的最小化子句。
The original all-UIP scheme [21] was never considered to be efficient enough to be part of SAT solvers, until the work by Feng & Bacchus [11]. We refer to their work for a detailed discussion on all-UIPs. Note that, Feng & Bacchus [11] consider their algorithm to be independent of minimization, more like a post-processing step, while we combine shrinking and minimization for improved efficiency. The technical report with the proofs of all theorems is available [13]. 译文:最初的全uip方案[21]从未被认为是有效的,足以成为SAT解决方案的一部分,直到Feng和Bacchus[11]的工作。我们参考他们的工作来详细讨论所有ui。注意,Feng & Bacchus[11]认为他们的算法与最小化无关,更像是一个后处理步骤,而我们将缩小和最小化结合起来以提高效率。所有定理证明的技术报告[13]。 |
|
2 Minimization
| We first present a formalization of what minimization actually achieves through the notion of “trail redundancy”. Then the classical deduced clause minimization algorithm is revisited. It identifies literals that are removable and others literals called poison that are not. The algorithm uses a syntactic criterion, but removes exactly the trail redundant literals. We present five existing criteria to detect (ir)redundancy earlier and prove their correctness. | |
| When a SAT solver identifies a conflicting clause, i.e., a clause in which all literals are assigned to false, it analyzes the clause and first deduces a 1stunique-implication-point clause [17,21]. This deduced clause is the starting point for minimization and shrinking. The goal is to reduce the size of this clause by removing as many literals as possible. The following redundancy criterion specifies if a literal is removable from the deduced clause. | |
|
译文:语义路径冗余
|
|
|
For this definition we only consider redundancy with respect to the reasons in the trail (ignoring other clauses in the formula). Note that, most SAT solvers only use the first clause in the watch lists to propagate, even though “better” clauses might trigger the same propagation. For instance PrecoSAT scans watch lists to find such cases [3]. However, due to potential cyclic dependencies, deducing the shortest learned clause is difficult [20]. 译文:对于这个定义,我们只考虑冗余的原因在trail(忽略公式中的其他子句)。请注意,大多数SAT求解器只使用监视列表中的第一个子句进行传播,即使“更好”子句可能触发相同的传播。例如,PrecoSAT扫描观察列表以发现此类病例[3]。然而,由于潜在的循环依赖关系,推断最短的学到的子句是困难的[20]。 |
|
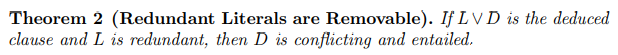 |
|
| Our next theorem states that the order of removal does not impact the outcome and that it is possible to cache whether a literal is (ir)redundant. | |
 |
|
|
The minimization algorithm is standard in SAT solvers with several improvements. First, they use efficient data structures to efficiently check if a literal is in the deduced clause. Second, they use caching: if a literal was deemed (un)removable before, the same outcome is used again. Caching successes and failures [19] make the algorithm linear in the size of the implication graph. Literals that can not be removed are called poison.
Our definition of trail redundancy is semantic, while the minimization algorithm uses relies on syntactic criteria to determine if a literal is removable or not. We show that both criteria are equivalent by using a result of Horn satisfiability. 译文:我们对尾迹冗余的定义是语义的,而最小化算法则依赖于语法标准来确定文本是否可删除。利用Horn可满足性的一个结果证明了两个准则是等价的。 |
|
 |
|
| The transition system from Definition 4 is not linear. As far we are aware, this is the first description of minimization algorithm in terms of Horn SAT. 译文:定义4中的过渡系统不是线性的。据我们所知,这是第一次用Horn SAT来描述最小化算法。 | |
 |
|
|
Theorem 6. Algorithm 1 is the same as the transition system from Definition 4. Theorem 7 (Equivalence Syntactic and Semantic Redundancy). Both notions of redundancy are equivalent. In particular, every redundant literal is also removable. |
|
 |
|
|
Our implementation relies on the alternative definition: It sorts the literals in the clause by its position on the trail. Each literal, starting from the lowest position, is checked. If it is not redundant, it is marked as present in the deduced clause for efficient checking. This reduces the number of flags (like testing if a literal is present in the deduced clause) to reset. Instead we could use d: When d = 0, the condition “L is in the deduced clause” does not apply.
Thanks to caching both successes and failures, the complexity is linear in the number of literals of the trail. Compared to our simple break conditions, more advanced criteria are possible. |
|
|
Theorem 9 (Poison Criteria). 1. If a literal appears on the trail before any other literal of the deduced clause on a decision level, then it is not redundant. 2. Literals with a decision level not in the deduced clause are not redundant. 3. Literals that are alone on a given decision level are not redundant (Knuth). |
|
 |
|
| The proof relies on the fact that the SAT solver propagates literals eagerly. This is not the case globally if the SAT solver uses chronological backtracking [15, 16] but remains correct for the reason clauses. The second and third point are widely used (e.g., in MiniSAT and Glucose), whereas the first one is a novelty of CaDiCaL and is not described so far. Root-level assigned false literals can also appear in deduced clauses and be removed without recursing over their reasons. | |
|
Theorem 10. Literals at level 0 are redundant. Algorithm 2 combines the two ideas that are described here, the caching and the advanced poison criteria. The ideas 1 and 3 from Theorem 9 require data structures that are not present in every SAT solver, namely the position τ of each literal in the trail. Doing so was not necessary until now, but it is required for shrinking. In our solvers, we also use the depth to limit the number of the recursive calls and avoid stack overflows. The implementation in MiniSAT [10] (and all derived solvers like Glucose [1]) uses a non-recursive version, but it requires two functions, one for depth zero and another for the recursive case. |
|
3 Shrinking
| After detecting conflicting clauses, the SAT solver analyzes them and deduces the first unique-implication point or 1-UIP [7], where only one literal remains on the current (largest) decision level. This is the first point where the clause is propagating, fixing the current search direction. The idea of 1-UIP can be applied on every level in order to produce shorter clauses. We call this process shrinking. It differs from minimization because it adds new literals to the deduced clause. | |
 |
|
| Algorithm 3: Shrinking algorithm min-alluip from Feng&Bacchus [11]. | |
| If fully applied, shrinking derives a subset of the decision-only clause. Therefore, it is limited. Feng & Bacchus [11] (abbreviated F&B from now on) have used various heuristics like not adding literals of low importance, without a clear winner across all implementations. We focus on their min-alluip variant. It applies the 1-UIP on every level. For each literal in the clause, the solver resolves with its reason unless a literals from a new level is added, thus making sure that the LBD or “glue” [1] is not increased, an important metric, which seems to relate well to the “quality” of learned clauses. In their implementation, if the clause becomes longer, the minimized clause would be used instead. | |
| Algorithm 3 shows the implementation of min-alluip. It considers the set of all literals of the deduced clause on the same level, or slice (same as a block if no chronological backtracking [15, 16] is allowed). Each slice is shrunken starting from the highest level. It resolves each literal of the slice with its reason or fails when adding new literals on lower levels. Because SAT solvers propagate eagerly, |B| ≥ 1 is an invariant of the while loop (and L cannot be a decision literal). | |
| The key difference between shrinking and minimization is that reaching the UIP is a global property, namely of all literals on a level, and not of a single literal. This means that testing redundancy is a depth-first search algorithm while shrinking is a breadth-first search algorithm on the implication graph. | |
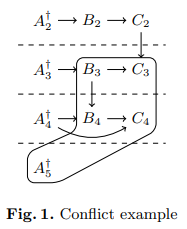 Fig. 1. Conflict example Fig. 1. Conflict example
|
|
| Example 11. Consider the implication graph from Figure 1. The algorithm starts with the highest level, namely with B4 and A4. The level is reduced to A4 introducing the already present B3. On the next level, C3 cannot be removed because it would import level 2. The resulting clause ¬A5 ∨¬A4 ∨¬A3 is smaller and is used instead of the original clause. | |
| F&B unfortunately do not provide source code nor binaries used in their experiments. Therefore we focus on their version of CaDiCaL submitted [14] to the SAT Competition 2020. It implements only one of their strategies, which, as far we can tell, matches the variant min-alluip [11] described above, while code for the other variants is incomplete or missing. | |
4 Minimizing and Shrinking
|
In contrast to F&B our algorithm minimizes literal slices of the deduced clause assigned on a certain level starting from the lowest to highest level. 译文:与F&B相反,我们的算法最小化了从最低层到最高层指定的推导子句的文字片。 This enables us to remove all redundant literals on-the-fly. After presenting our algorithm we study its complexity and then discuss its implementation in our SAT solvers CaDiCaL, Kissat, and Satch. |
|
| The main loop of our Algorithm 4 interleaves shrinking and (if shrinking failed) minimization. For each slice of literals in the deduced clauses assigned on a certain level we then attempt to reach the 1-UIP, similarly to Algorithm 3. If this fails, we minimize the slice. This also allows to lift some restriction on shrinking: only non-redundant literals interrupt the search for the 1-UIP. We start from the lowest level to keep completeness of minimization. | |
 |
|
 |
|
| Algorithm 4: Our new method for integrated shrinking with minimization. | |
| As mentioned before, for efficiency a cache is maintained during minimization to know whether a literal is redundant or not. | |
|
Theorem 13 (Shrinking and Redundancy). Redundant literals remain redundant during shrinking. Theorem 13 ignores irredundant literals because new literals are added to the deduced clause, allowing for more removable literals. This explains why F&B propose (in one variant of shrinking) to minimize again after shrinking. For the same reason we do not check if literals are redundant on the current level, since added literals (e.g., new 1st UIPs) invalidate the literals marked as “poisoned”. Instead, we check for redundancy of literals on lower levels and on current level only after shrinking them, when the literals on the slice level are fixed. |
|
 |
|
| To keep the complexity linear, when interleaving minimization with shrinking as shown in Algorithm 4, we maintain a global shared minimization cache, not reset between minimizing different slices. A more complicated solution consists in minimizing up-front (as in the implementation of F&B in [14]), followed by shrinking, and if shrinking succeeds, reset the poison literals on the current level. | |
| Resetting only literals on the current level is important for reducing the runtime complexity from quadratic to linear in the size of the implication graph. As we are shrinking “in order” (from lowest to highest decision level) we can keep cached poisoned (and removable) literals from previous levels, thus matching the overall linear complexity of (advanced) minimization. | |
| Our solution also avoids updating the minimization cache more than once during shrinking. When a slice is successfully reduced to a single literal, all shrunken literals are marked as redundant in the minimization cache. The process is complete in the sense that no redundant literals remain. | |
|
Theorem 15 (Completeness). All redundant literals are removed. This result relies on the fact that during the outer loop no literal on a lower level is added to the deduced clause. If this would be allowed (as in Algorithm 3), the poisoned flag has to be reset and minimization redone, yielding a quadratic algorithm. However, the theorem says nothing about minimality of the shrunken clause if we allow to add new literals, as in the following example. |
|
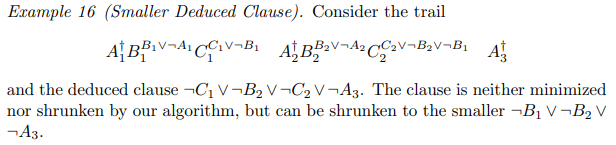 |
|
| In Algorithm 4, on the one hand, shrinking could use a priority queue (implemented as binary heap) to determine the last assigned literal in B. Then for each slice, we have a complexity of O(nb log nb) for shrinking where nb is the number of literals at the slice level in the implication graph. On the other hand, minimization of all slices is linear in the size of the implication graph. Overall the complexity is O(glue · n log n) where the “glue” is the number of different slices (and a number that SAT solvers try to reduce heuristically) and n the maximum of the nb. However, note that, bumping heuristics require sorting of the involved literals anyhow either implicitly or explicitly [6]. | |
| Instead of representing the slice B as a priority queue, implemented as binary heap, to iterate over its literals, it is also possible to iterate over the trail directly as it is common in conflict analysis to deduce the 1st-UIP clause. Without chronological backtracking, the slices on the trail are disjoint and iterating over the trail is efficient and gives linear complexity O(|glue|×|max trail slice length|), i.e., linear in the size of the implication graph. | |
| With chronological backtracking slices on the trail are not guaranteed to be disjoint. Therefore, in the worst case, iterating over a slice along the trail might require to iterate over the complete trail. In principle, this could give a quadratic complexity for chronological backtracking without using a priority queue for B. In our experiments both variants produced almost identical run-times and thus we argue that the simpler variant of going over the trail should be preferred. | |
| We have implemented the algorithm from the previous section in our SAT solvers CaDiCaL [5], Kissat [5], and Satch [4]. The implementation is part of our latest release in the file shrink.c (shrink.cpp for CaDiCaL).1 Note that, Satch is a simple implementation of the CDCL loop with restarts and was written to explain CDCL. It does not feature any in- nor preprocessing yet. | |
| We either traverse the trail directly or use a radix heap [8] as priority queue. Unlike the implementation by F&B, our priority queue contains only the literals from the current slice until either shrinking fails or the 1-UIP is found. It allows for efficient popping and pushing trail positions. Note that, radix heaps require popped elements to be strictly decreasing, and as the analysis follows reverse trail order, we first compute the maximum trail position of literals in the considered slice and then index literals by their offsets on the tail from this maximum trail position. The literal position in the trail is not cached in every SAT solver, but was already maintained in Kissat and CaDiCaL. | |
5 Experiments
| We have implemented our algorithm in the SAT solvers CaDiCaL, Kissat (the winner of the SAT Competition 2020), and Satch and evaluated them on benchmark instances from the SAT Competition 2020 on an 8-core Intel Xeon E5-2620 v4 CPUs running at 2.10 GHz (turbo-mode disabled). For both tracks we used a memory limit of 128 GB (as in the SAT Competition 2020). We tested 3 configurations, shrink (shrinking and minimizing), minimize, and no-minimize (neither shrinking nor minimizing). Due to space constraint we only give graphs for some solvers but findings are consistent across all of them. 译文:由于空间限制,我们只给出了一些解算器的图,但所有解算器的结果都是一致的。 | |
|
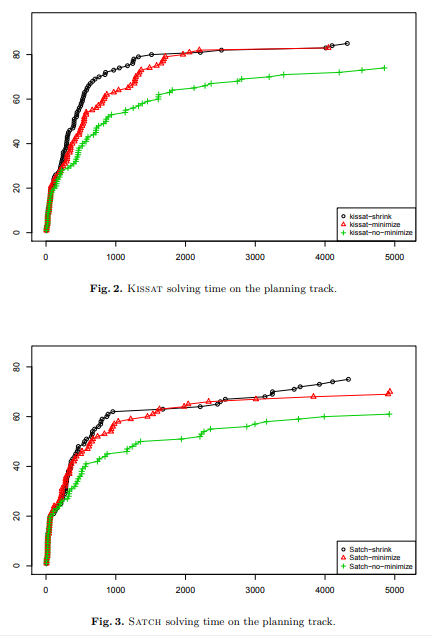
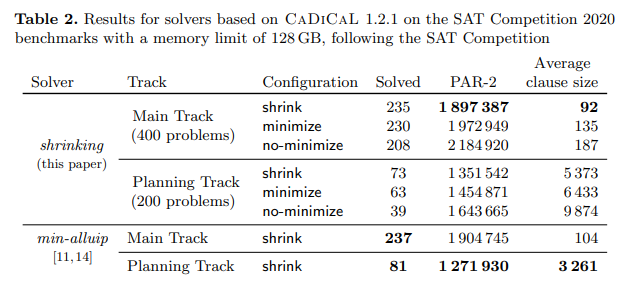
Tables 1 for Kissat and Satch show that minimization is more important than shrinking, but the latter still improves performance for Kissat. In the planning track, running time decreases significantly, whereas the impact on the main track is smaller. Compared to the main track, the planning problems require much more memory and memory usage drops substantially with shrinking. For Satch, we observe a slight performance decrease. Figures 2 and 3 show that even if shrinking solves only a few more problems, the speedup is significant. 译文:表1显示了最小化比收缩更重要,但后者仍然可以提高Kissat的性能。 |
|
| ven if shrinking solves only a few more problems, the speedup is significant. In all our SAT solvers we distinguish between focused mode (many restarts) and stable mode (few restarts). Note that CaDiCaL uses the number of conflicts to switch between these modes which is rather imprecise: in stable mode decision frequency is lower while the conflicts frequency is higher compared to focused mode and accordingly the fraction of running time spent in conflict analysis and thus minimization and shrinking increases in stable mode compared to focused mode. To improve precision both Kissat and Satch measure the time by estimating the number of possible cache misses instead, called “ticks” [5]. By default Kissat also counts the number of such ticks during shrinking and minimization. To avoid the bias introduced by this technique in terms of influencing mode switching we deactivated this feature in our experiments (only for Kissat). | |
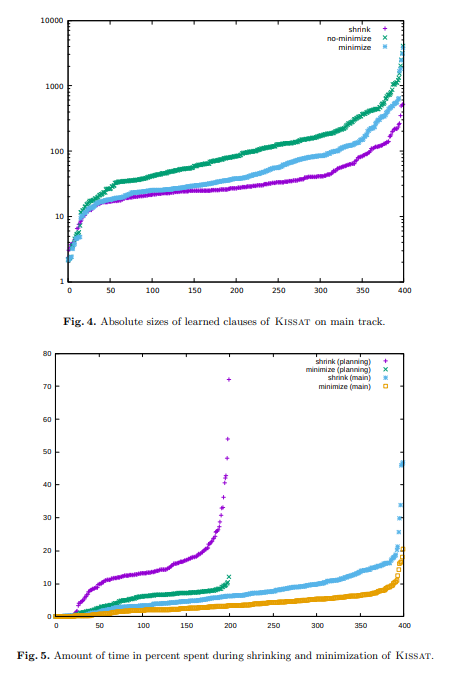
| We analyzed the results on the main track in more details over all instances (i.e., until timeout or memory out), not only over solved instances. The amount of time (in percentage of the total) more than doubles when activating shrinking: it goes from 6.3 % to 14.3 % of the total amount of time (Figure 5). However, the size of the clauses is reduced with a similar ratio: It drops from 110 to 46 (183 without minimization). On the planning track, it drops from 13 076 to 5 398 literals on average (16 637 without minimization). | |
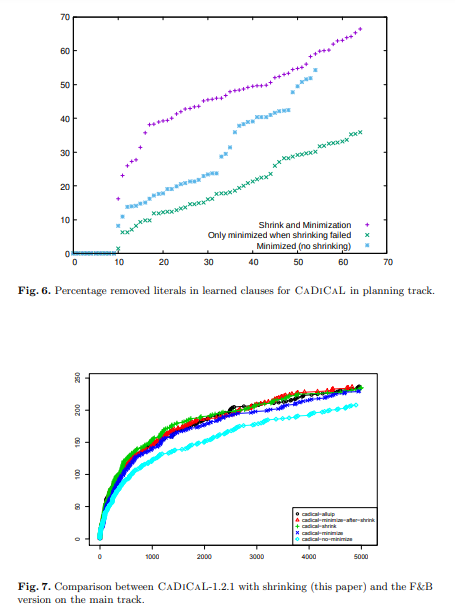
| To compare our method to the min-alluip implementation, which is based on CaDiCaL 1.2.1, we backported our shrinking algorithm to CaDiCaL 1.2.1 too. The results are in Table. 2. The only difference is the shrinking algorithm, hence there are not differences for the minimize and no-minimize configuration. The F&B version performs slightly better than our version. An interesting observation is that CaDiCaL 1.2.1 learns much larger clauses than Kissat and Satch but also larger than the latest CaDiCaL version. The effect can be partially explained by the stable mode that is much longer than on the other solvers. We have also experimented with minimizing separately from shrinking instead of combining them. As long as the cache is shared there is very little performance difference. Figure 7 shows the CDF for the main track. | |
|
|
|
Fig. 2. Kissat solving time on the planning track. Fig. 3. Satch solving time on the planning track. |
|
|
|
|
Fig. 4. Absolute sizes of learned clauses of Kissat on main track. Fig. 5. Amount of time in percent spent during shrinking and minimization of Kissat. |
|
|
|
|
Fig. 6. Percentage removed literals in learned clauses for CaDiCaL in planning track Fig. 7. Comparison between CaDiCaL-1.2.1 with shrinking (this paper) and the F&B version on the main track. |
|
|
Figure 6 shows percentages of removable literals on the planning track. Shrinking removes more literals than the subsequent minimization (and more than minimization alone). We have mentioned the complexity difference between using a radix heap and iterating over the trail. 译文:收缩移除的字面值比随后的最小化移除的字面值更多(而且不仅仅是最小化)。我们已经提到了使用基数堆和遍历路径之间的复杂性差异。 |
|
 |
|
|
We have implemented both versions in our three SAT solvers. We compare both version but could not observe any significant difference. We believe that this is due to the fact that finding the next literal is actually very efficient: it is in the trail (that is in cache anyways) and we check a single flag. We attempted to force the worst case by enforcing chronological backtracking, but performance remained similar. 译文:我们比较了两个版本,但没有观察到任何显著差异。我们认为这是因为找到下一个文字实际上是非常有效的:它在路径中(无论如何都在缓存中),我们检查一个标志。我们试图通过强制执行时间回溯来强制执行最坏的情况,但性能仍然相同。
学习注释:在2021年竞赛的说明中,该作者发现并纠正了存在的问题。
Finally, and most importantly, the version of CADICAL submitted to the SAT Competition 2020 unfortunately failed to export the assignment found in local search minimizing the number of falsified clauses back to the CDCL loop as saved phases (due to a change in semantics of copy_phases), which in essence rendered the local search component completely useless. 译文:最后,也是最重要的,提交到2020年SAT竞赛的CADICAL版本不幸地未能将在本地搜索中找到的作业导出到CDCL循环作为保存阶段(由于copy_phases的语义变化),从而最小化了伪造子句的数量。这在本质上使得本地搜索组件完全无用。 And indeed, our post-competition experiments showed, that this “heuristic bug” resulted in solving fewer instances during the competition. 译文:事实上,我们的比赛后实验表明,这个“启发式错误”导致在比赛期间解决的实例更少。 In version 1.4.0 saved phases are again explicitly overwritten at the end of local search with the minimum assignment found during local search. 译文:在1.4.0版本中,保存的阶段在本地搜索结束时再次显式重写,使用在本地搜索期间找到的最小赋值。
On top of version 1.4.0 of CADICAL, as used in the “CADICAL hack track”, we have added a light version of Like the original version [7], our version [8] shortens learned clauses by calculating the unique implication 译文:与原始版本[7]一样,我们的版本[8]通过计算冲突子句每一层的唯一隐含点(UIP)来缩短学习子句,限制在较低的层次上不添加文字。
Unlike Feng & Bacchus’s version, our algorithm is efficient enough to be executed unconditionally and minimizes the clause at the same time. 译文:我们的算法是有效的,可以无条件地执行,同时最小化子句
|
|
6 Conclusion
|
We presented a simple linear algorithm which integrates minimization and shrinking and is guaranteed to remove all redundant literals. 译文:我们提出了一种简单的线性算法,它集最小化和收缩为一体,保证消除所有冗余字元。 In practice it can be run to completion unconditionally. Our implementation and evaluation with several SAT solvers show the benefit of our approach and confirm effectiveness of shrinking in general. 译文:在实践中,它可以无条件地运行到完成。我们的实施和评估与几个SAT求解器显示了我们的方法的好处,并确认了一般收缩的有效性。 An open question is how to extend our notion of trail redundancy to capture that new literals can be added in order to reduce size. This would allow to formulate completeness of shrinking in the same way as we did for minimization. 译文:一个有待解决的问题是,如何扩展跟踪冗余的概念,以捕获可以添加新的文字以减少大小。这样就可以用最小化的方法来表示收缩的完整性。 |
|
References
|
References 1. Audemard, G., Simon, L.: Predicting learnt clauses quality in modern SAT solvers. In: IJCAI. pp. 399–404 (2009), http://ijcai.org/Proceedings/09/Papers/074. pdf 2. Biere, A.: CaDiCaL, Lingeling, Plingeling, Treengeling and YalSAT entering the SAT Competition 2018. In: Heule, M., J¨arvisalo, M., Suda, M. (eds.) Proc. of SAT Competition 2018 – Solver and Benchmark Descriptions. Department of Computer Science Series of Publications B, vol. B-2018-1, pp. 13–14. University of Helsinki (2018) 3. Biere, A.: Lingeling, Plingeling, PicoSAT and PrecoSAT at SAT Race 2010. Tech. rep., FMV Reports Series, Institute for Formal Models and Verification, Johannes Kepler University (aug 2021) 4. Biere, A.: The SAT solver Satch. Git repository (2021), https://github.com/ arminbiere/satch, last Accessed: March 2021 5. Biere, A., Fazekas, K., Fleury, M., Heisinger, M.: CaDiCaL, Kissat, Paracooba, Plingeling and Treengeling entering the SAT Competition 2020. In: Balyo, T., Froleyks, N., Heule, M., Iser, M., J¨arvisalo, M., Suda, M. (eds.) Proc. of SAT Competition 2020 – Solver and Benchmark Descriptions. Department of Computer Science Report Series B, vol. B-2020-1, pp. 51–53. University of Helsinki (2020) 6. Biere, A., Fr¨ohlich, A.: Evaluating CDCL variable scoring schemes. In: Heule, M., Weaver, S.A. (eds.) SAT 2015. LNCS, vol. 9340, pp. 405–422. Springer (2015). https://doi.org/10.1007/978-3-319-24318-4 29 7. Biere, A., Heule, M.J.H., van Maaren, H., Walsh, T. (eds.): Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, vol. 185. IOS Press (2009) 8. Cherkassky, B.V., Goldberg, A.V., Silverstein, C.: Buckets, heaps, lists, and monotone priority queues. SIAM J. Comput. 28(4), 1326–1346 (1999). https://doi.org/10.1137/S0097539796313490 9. Dowling, W.F., Gallier, J.H.: Linear-time algorithms for testing the satisfiability of propositional Horn formulae. J. Log. Program. 1(3), 267–284 (1984). https://doi.org/10.1016/0743-1066(84)90014-1 10. E´en, N., S¨orensson, N.: An extensible SAT-solver. In: SAT. LNCS, vol. 2919, pp. 502–518. Springer (2003). https://doi.org/10.1007/978-3-540-24605-3 37 11. Feng, N., Bacchus, F.: Clause size reduction with all-UIP learning. In: SAT. LNCS, vol. 12178, pp. 28–45. Springer (2020). https://doi.org/10.1007/978-3-030-51825- 7 3 12. Fleury, M.: Formalization of logical calculi in Isabelle/HOL. Ph.D. thesis, Saarland University, Saarbr¨ucken, Germany (2020), https://tel.archives-ouvertes.fr/ tel-02963301 13. Fleury, M., Biere, A.: Efficient all-UIP learned clause minimization (extended version). Tech. Rep. 21/3, Johannes Kepler University Linz, FMV Reports Series, Institute for Formal Models and Verification, Johannes Kepler University, Altenbergerstr. 69, 4040 Linz, Austria (2021). https://doi.org/10.350/fmvtr.2021- 3, https://doi.org/10.350/fmvtr.2021-3 14. Hickey, R., Feng, N., Bacchus, F.: Cadical-trail, Cadical-alluip, Cadical-alluip-trail and Maple-LCM-Dist-alluip-trail at the SAT Competition. In: Balyo, T., Froleyks, N., Heule, M., Iser, M., J¨arvisalo, M., Suda, M. (eds.) Proc. of SAT Competition 2020 – Solver and Benchmark Descriptions. Department of Computer Science Report Series B, vol. B-2020-1, p. 10. University of Helsinki (2020) Efficient All-UIP Learned Clause Minimization 17 15. M¨ohle, S., Biere, A.: Backing backtracking. In: SAT. LNCS, vol. 11628, pp. 250–266. Springer (2019). https://doi.org/10.1007/978-3-030-24258-9 18 16. Nadel, A., Ryvchin, V.: Chronological backtracking. In: SAT. LNCS, vol. 10929, pp. 111–121. Springer (2018). https://doi.org/10.1007/978-3-319-94144-8 7 17. Silva, J.P.M., Lynce, I., Malik, S.: Conflict-driven clause learning SAT solvers. In: Biere, A., Heule, M., van Maaren, H., Walsh, T. (eds.) Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, vol. 185, pp. 131–153. IOS Press (2009). https://doi.org/10.3233/978-1-58603-929-5-131 18. S¨orensson, N., Biere, A.: Minimizing learned clauses. In: SAT. LNCS, vol. 5584, pp. 237–243. Springer (2009). https://doi.org/10.1007/978-3-642-02777-2 23 19. Van Gelder, A.: Improved conflict-clause minimization leads to improved propositional proof traces. In: SAT. LNCS, vol. 5584, pp. 141–146. Springer (2009). https://doi.org/10.1007/978-3-642-02777-2 15 20. Van Gelder, A.: Generalized conflict-clause strengthening for satisfiability solvers. In: SAT. Lecture Notes in Computer Science, vol. 6695, pp. 329–342. Springer (2011). https://doi.org/10.1007/978-3-642-21581-0 26 21. Zhang, L., Madigan, C.F., Moskewicz, M.W., Malik, S.: Efficient conflict driven learning in Boolean satisfiability solver. In: ICCAD. pp. 279–285. IEEE Computer Society (2001). https://doi.org/10.1109/ICCAD.2001.968634 |
|





