文献学习-The Community Structure of Constraint Satisfaction Problems and Its Correlation with Search Time

The Community Structure of Constraint Satisfaction Problems and Its Correlation with Search Time

M. Medema and A. Lazovik, "The Community Structure of Constraint Satisfaction Problems and Its Correlation with Search Time," 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), 2020, pp. 153-160, doi: 10.1109/ICTAI50040.2020.00034.

---

 CSP ---- Constraint satisfaction problem

 原约束图[10]    Incidence Graph

对偶约束图[10]

关联图   Incidence Graph

 

Abstract:

Constraint satisfaction problems are, in general, NP-complete problems, meaning that the computational complexity increases exponentially with the size of the problem in the worst case, under the assumption that P does not equal NP. The structure of a problem heavily influences its computational complexity, however, and problems with a restricted structure constitute one of the general classes of tractable problems. This paper explores the community structure of constraint satisfaction problems, a type of structure already found to be important for SAT problems that is inherent to certain real-world domains. The community structure of the instances of the MiniZinc Challenge of 2019 was identified, and its correlation with the search times of four state-of-the-art solvers as well as with the tree-width of the instances was analysed. The results reveal the strong community structure of many of the instances, although the strength of the community structure seems to only marginally affect the search times. On the other hand, a strong correlation between the community structure and the tree-width is observed, where stronger community structure suggests better decomposability. Taking community structure into account more explicitly during the search process may, therefore, allow constraints solvers to solve problems with strong community structure more efficiently.

SECTION I.

Introduction

	Constraint Satisfaction Problems (CSPs) are a generic type of search problem that can model numerous types of problems from a myriad of different domains [1]. A CSP consists of a set of variables, with corresponding domains, and a set of constraints that impose restrictions on the values that can be assigned to the variables. The goal is to find assignments to the variables from their respective domains such that all the constraints are satisfied or to find that no such solution exists.
	Finding a solution to a CSP is, in general, an NP-complete problem, meaning that, under the assumption that P≠NP, the time required to find a solution to a problem grows exponentially with the size of the problem in the worst case [2]. The structure of a problem, formed by the interactions between the constraint scopes, has a strong influence on its complexity, however. Problems with a restricted structure comprise one of the general classes of tractable problems [3], and polynomial-time algorithms, for example, exist for CSPs that are tree-structured [2]. Decomposition methods generalise the notion of tree-structure, resulting in another class of tractable problems consisting of problems with low tree-width [4]. More generally, a particular structure oftentimes allows a solution to be found considerably faster than the worst-case exponential complexity, as is frequently the case for real-world problems.
	Community structure, which is an important property that often appears in real-world networks, may have similar potential, as has already been demonstrated for SAT problems [5]. A CSP with a strong community structure consists of small groups of strongly interconnected variables, where, except for a small number of connections, these communities could be largely considered as independent problems. For example, for building automation systems or smart energy systems, the communities may correspond to the physical structure of the domain, such as the rooms of a building, where the communities provide a natural boundary for the constraints.
	In this paper, the importance of community structure is established by analysing the community structure of a set of CSP instances. In addition to that, it investigates what effect the community structure has on the performance of several state-of-the-art constraint solvers, and whether the strength of the community structure, possibly together with other features of a particular problem, serves in any way as a meaningful indicator of the time it takes a constraint solver to find a solution to a problem. The community structure of a problem instance is also compared to its tree-width to determine to what extent these two measures coincide.
	The paper is structured as follows. Section II discusses related work that has investigated community structure in other contexts. Section III provides details regarding community detection for CSPs, and the set of problems that is analysed is presented in section IV. Sections V, VI and VII present the modularity results, the correlation with the search time and the correlation with tree-width, respectively. Finally, the paper is concluded, and directions for future work are provided.

SECTION II.

Related Work

	Problems with strong community structure frequently appear across multiple domains [6], [7]. Ansótegui et al. computed the modularity of the SAT instances of the SAT Race Finals of 2010, a set of problems with industrial relevance, revealing the strong community structure of many of these instances [6]. For several classes of random instances of Model RB, Li et al. have shown that the instances exhibit fairly strong community structure, although the modularity decreases as the number of constraints, the arity of the constraints and, to some extent, the number of variables increases [7]. Many real-world CSP instances are not random problems, however, and, like SAT instances where the community structure of random instances is considerably lower, these results may not directly apply to other classes of problems [6]. This work considers a broad set of CSP instances, including problems with industrial relevance. Besides identifying the community structure of these problems, it also investigates the correlation between the community structure and the duration of the search process.
	Fig. 1. An example of a graph with community structure.
	Besides the existence of community structure, Newsham et al. also established a correlation between the community structure and the search time of conflict-driven clause-learning SAT solvers [8]. The authors show that the Literal Block Distance, a measure that indicates the importance of a clause learnt during the search process, strongly correlates with the number of communities for many instances. Furthermore, through the use of linear regression, they showed that the modularity is an important feature in the regression model for predicting the search time of SAT solvers. The number of communities alone is also highly influential, more so than the number of variables and clauses.
	Based on the concept of community structure, Ganian and Szeider defined the notion of h-modularity, a measure that is similar to tree-width, and introduced an algorithm for which SAT problems are fixed-parameter tractable when parameterised by the h-modularity [5]. This algorithm makes explicit use of the existence of community structure in SAT formulas, making it possible to solve SAT instances with small h-modularity even if the values of other parameters would normally render the instance unsolvable.

SECTION III.

Community Detection for CSPs

	A network or graph has community structure if the set of vertices can be partitioned such that the vertices within each partition are densely connected and the vertices of different partitions sparsely connected [9]. An example of a graph with community structure is shown in Figure 1.
	The modularity is a frequently used measure that expresses the quality of a partitioning of the vertices of a graph, thereby providing information regarding the existence of community structure [10], [11]. For a given partition, it measures the fraction of edges within each community compared to the fraction of edges between the communities [10]. The value of the modularity ranges between −1.0 and 1.0, where a value closer to 1.0 signifies a better partitioning for which the fraction of edges within the communities is higher than between the communities. With this measure, the problem of identifying the communities reduces to finding the partitioning that maximises the modularity. 译文：有了这种方法，识别社区的问题就简化为找到最大化模块化的分区。
	The incidence graph is a bipartite graph where the sets of vertices represent the variables and constraints, respectively. An edge connects a variable to a constraint if the scope of the constraint includes that variable. This representation captures the full structure of the problem, similar to the constraint hypergraph.
	Definition 1 SECTION Definition 1 Incidence Graph Representation
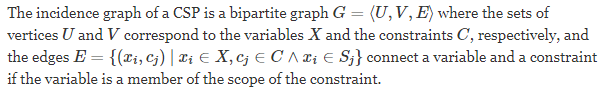	The primal constraint graph includes a vertex for each of the variables of the problem, and an edge connects two variables if there exists a constraint scope of which both variables are a member. 译文：原始约束图包含问题的每个变量的一个顶点，如果存在一个约束范围，两个变量都是其中的成员，则用一条边连接两个变量。 This representation does not retain all information about the problem, as a clique in the graph can, for example, correspond to both a single constraint scope or multiple overlapping constraint scopes. 译文：这种表示并不保留关于问题的所有信息，例如，图中的团既可以对应单个约束范围，也可以对应多个重叠的约束范围。
	Definition 2 SECTION Definition 2 Primal Constraint Graph
	A similar graphical model that focuses on the constraints instead of the variables is the dual constraint graph, where the vertices represent the constraint scopes, and an edge exists between two constraint scopes if they have at least one variable in common.
	Definition 3 SECTION Definition 3 Dual Constraint Graph
	Finding the partitioning of the vertices of a graph that maximises the modularity is, unfortunately, an NP-hard problem, making it unsuitable for all but the smallest graphs [9]. 译文：不幸的是，找到一个图的顶点的划分，使其模块化最大化是一个np困难的问题，这使得它不适用于除了最小的图[9]之外的所有图 Heuristic-based algorithms generally manage to find good partitions, however, and also work for larger graphs. 译文：然而，基于启发式的算法通常能够找到好的分区，也适用于更大的图。 In this work, the Louvain algorithm, which finds good partitions and has a relatively small computational complexity, is used to analyse the community structure of the primal and dual constraint graphs [10]. 译文：本文采用Louvain算法对原约束图[10]和对偶约束图[10]的群体结构进行了分析，该算法发现了较好的分区，计算复杂度也相对较小。 For the incidence graph, the BiLouvain algorithm is used, because the Louvain algorithm only works for unipartite graphs [15], and while it is possible to represent the incidence graph as a unipartite graph, this conversion could result in a loss of information. 译文：对于关联图，我们使用了BiLouvain算法，因为Louvain算法只适用于单部图[15]，虽然可以将关联图表示为单部图，但是这种转换可能会导致信息的丢失。

 

SECTION IV.

Analysing MiniZinc Instances

	The analysis focuses on the community structure of the CSP instances of the MiniZinc Challenge of 2019 [16]. This set comprises twenty classes of problems, each containing five instances, with both academic and industrial relevance, which should provide a comprehensive evaluation of the community structure of CSPs.
	All of the problem instances are MiniZinc specifications that must first be compiled to FlatZinc before it is possible to obtain their graph representations [17]. The result of the compilation step is not necessarily unique, however, as it strongly depends on which constraints are made available to the compiler. The FlatZinc representation often also includes variables for which a constraint uniquely defines its value after reducing the remaining variables in its scope to a single value.
	During the search process, a solver may safely ignore these defined variables since the constraints ultimately define their values based on the values of the other variables. The community structure of a graph representation will generally be vastly different depending on whether the defined variables are included, however, and while it is also important to analyse the complete version of the problem to grasp its overall structure, a version that does not include these defined variables may align more closely with the implicit representation that constraint solvers use during the search.
	\begin{equation*}\Delta (x_{i},\hat{C})=\begin{cases} \bigcup\limits_{c_{j}\in\phi(x_{i},\hat{C})}S_{j}\backslash \{x_{i}\} &\text{if}\ x_{i}\in X^{D}\\ \bigcup\limits_{c_{j}\in\kappa(x_{i},\hat{C})}S_{j}\backslash \{x_{i}\} &\text{if}\ x_{i}\in X^{R}\\ \{x_{i}\} &\text{otherwise}\end{cases} \end{equation*}
	\begin{equation*}\Psi(x, S,\hat{C})=\begin{cases} S\backslash \{x\}\cup\Delta(x,\hat{C}) &\text{if}\ x\in S\\ S &\text{otherwise}\end{cases} \end{equation*}
	The full reduction of a FlatZinc instance is the problem where all the defined variables have been replaced. 译文：当所有已定义的变量都被替换时，FlatZinc实例的完全缩减就会出现问题。
	Definition 4 SECTION Definition 4 Full Reduction
	After obtaining the full reduction, the objective function is also removed. The generally strong dependencies that this function introduces between the variables are not strict: for all the instances considered here, the objective function is a simple linear function that can be decomposed into several smaller objective function. 译文：在得到完全约简后，也去掉目标函数。这个函数在变量之间引入的一般强依赖性并不严格:对于这里考虑的所有实例，目标函数是一个简单的线性函数，可以分解成几个较小的目标函数。

 

SECTION V.

Community Structure of CSPs

	In order to identify the community structure of the set of problems of the MiniZinc Challenge of 2019, the MiniZinc models are compiled, using version 2.4.3 of the MiniZinc IDE, for Choco 4.0.4 [18], OR-Tools 7.6 [19], Gecode 6.2.0 [20] and Chuffed 0.10.4 [21], four state-of-the-art constraint solvers that each support a different set of constraints, making it possible to assess the influence that custom constraints have on the community structure. For the same purpose, a reference set is created by compiling all the MiniZinc models using only the default set of constraints included in the standard MiniZinc library. The full reduction is computed for each of the FlatZinc instances produced by the compiler, and for both the original FlatZinc instance and its reduction, the graph representations are obtained, where the community structure of the primal constraint graph and dual constraint graph is analysed using the Louvain algorithm, and the community structure of the incidence graph is analysed using the BiLouvain algorithm. Four classes have been excluded from the analysis because too much time was required to either compile the model or analyse its graph representation. Specifically, the instances of the “code-generator”, “nside”, “ptv” and “rcpsp-wet-diverse” classes were excluded, as well as instance “n37” of the “triangular” class.
	Table I The average modularity, together with the standard deviation in parentheses, for each class of problem instances of the MiniZinc challenge of 2019. The second column indicates the type of graphical model, where the incidence graph, primal graph and dual graph has been encoded as I, P and D, respectively. Instances with a modularity value of 0.3 or higher have been highlighted.
	Table I reports the average modularity, together with the standard deviation, per class of problems for each collection of instances, showing both the community structure of that particular class and how much it differs among the different instances of that class. The second column indicates the type of graphical model, where the incidence graphs, primal graphs and dual graphs have been encoded as I, P, and D, respectively. A modularity value of 0.3 or higher signifies a strong community structure; the grey-coloured cells highlight these instances. Moreover, by design, a partitioning where all the vertices reside in their own community or where all vertices are part of the same community have a modularity value of 0.0.
	For most classes, at least one of the graphical models exhibits a strong community structure, and often the modularity is high for all three types of graphs; the highest modularity is generally observed for the dual constraint graph. There are also cases where one of the graphical models does not seem to have any community structure, while the community structure of the remaining two graphs is fairly strong. For such occurrences, the community structure of the primal constraint graph is principally nonexistent, which could suggest the inability of this graph representation to capture the structure of the problem in certain cases (using a weighted version of the graph seemed to make little difference). Other classes, such as multi-knapsack, do not seem to have any community structure, regardless of the graph representation. This result is expected, as the constraints that are involved in the knapsack problem include all the variables, making a single community, which has a modularity value of 0.0, the only reasonable partitioning.
	The modularity of the reduction is almost always lower than the full version. This version only includes the search variables and replaces all the defined variables in the scopes of the constraints, which often results in more densely connected graphs as the scopes include many of the same variables. Occasionally, the modularity of the reduction is slightly higher, something that may happen when there are no defined variables but the removal of the objective function eliminates several connections between variables and constraints. The community structure of this version may be more important for certain techniques, however, as it may be more representative of how those techniques perceive a particular problem.
	The standard deviation shows that the modularity is fairly consistent within a particular class of problems, meaning the community structure is either strong or weak for all of the instances. An example of an exception to this is liner-sf-repositioning, for which the standard deviation is 0.20 or higher for some of the graph representations. Possibly, this difference can be attributed to the types of constraints that are used in those instances.
	Some important differences between the modularity of the different solvers are apparent. Usually, the difference in modularity is negligible; it is either the same or differs by less than 0.05. 译文：不同求解器的模块性之间的一些重要差异是显而易见的。通常，模块化的差异是可以忽略不计的;它要么相同，要么相差小于0.05。   For example, for liner-sf-repositioning the modularity is nearly identical, both between the solvers and between the solvers and the reference set. In other cases, these differences are more substantial, such as for zephyrus, where two distinct groups are recognisable. The modularity for Choco and Gecode are almost identical, as are the modularity values of the remaining solvers and the reference set. The first two seemingly support a constraint, or lack this support, leading to a different representation with, in this particular instance, weaker community structure. The set of constraints supported by a solver conceivably affects the community structure, although the majority of the classes seem to include constraints that are commonly supported by all solvers.

 

SECTION VI.

Correlating Community Structure and Search Time

	To uncover a potential correlation between the search time and the community structure, the search times of the four solvers are recorded for all of the CSP instances. Each solver solves the solver-specific version as well as the reference version of an instance, both following the search specification and using “free search”, which allows a solver to disregard the search specification. A time limit of 30 minutes is imposed, and the search time of any instance that was not solved within this limit is set to 30 minutes. All experiments were performed on the HPC cluster of the University of Groningen, where each search process was granted a single core of one of the two Intel Xeon E5 2680v3 CPUs and 3GB of memory.
	The results include only the search times of the solver-specific versions for which the solvers followed the search specification; all the solvers solved fewer instances of the reference set, although some instances required less time to solve, and even though the “free search” resulted in a considerable increase in the number of solved instances for all but Choco, the correlations are remarkably similar. For the instances of the “kidney-exchange” and “lot-sizing” classes, OR-Tools and Chuffed raised an exception, caused by the lack of support for the “indomain_median” heuristic that is included in the search specification. These instances have not been excluded from the experiments, however, because of the limited impact it had on the results.
	Correlations are analysed between the community structure, consisting of the modularity, the number of communities and the maximum community size, and several other features of the problems, including the search time, the number of variables, the number of constraints, the domain size and the average and maximum degree (the average and maximum size of the constraint scopes, respectively). 译文：分析了由模块化、群落数量和最大群落规模组成的群落结构与问题的其他几个特征之间的相关性，包括搜索时间、变量数量、约束数量、域大小和平均和最大程度(分别是约束范围的平均和最大大小)。 The Spearman's rank correlation coefficient, which can detect more general relations besides linear ones, is used to compute the strength of the relationships between these features.
	Fig. 2. The spearman correlation between the community structure and other features of the complete versions of the problem instances. The columns represent choco, OR-tools, gecode and chuffed, respectively, and the rows correspond to the primal graph, dual graph and the incidence graph.
	Fig. 3. The spearman correlation between the community structure and other features of the reduced versions of the problem instances. The columns represent choco, OR-tools, gecode and chuffed, respectively, and the rows correspond to the primal graph, dual graph and the incidence graph.
	Figures 2 and 3 show the correlation coefficients of the different combinations of features for the complete problem and the reduction, respectively. In general, the search times are lower for problem instances with higher modularity, whereas the maximum community size and, to some extent, the number of communities, suggest a higher search time; the correlations between these features are often fairly weak, however. 译文：图2和图3分别显示了完全问题和约简的不同特征组合的相关系数。一般来说，模块化程度越高的问题实例的搜索次数越少，而最大社区规模和社区数量在一定程度上表明搜索时间越长;然而，这些特征之间的相关性往往相当弱。 Increasing the number of variables or constraints leads to higher modularity, more communities and larger communities, except for some of the reductions, where increasing the number of constraints has the opposite effect. A higher average degree, on the other hand, implies fewer communities that are more strongly connected. The features of the community structure also appear to be strongly correlated, but the actual correlation varies greatly from strongly positive to strongly negative. These observations are highly consistent between the different solvers, and even for the reductions the coefficients largely coincide, although those are closer to zero. Only between the various graphical models, larger differences are discernible, where the strongest correlations are typically reserved for the dual constraint graphs.
	Individually, the features that capture the community structure only seem to have a marginal influence on the search time. Given the complex nature of CSPs and the many factors that potentially influence the search time, combining multiple features may provide a better model of the search time. 译文：单独而言，捕捉社区结构的特征似乎只对搜索时间有很小的影响。考虑到csp的复杂性和可能影响搜索时间的许多因素，结合多个特征可能提供一个更好的搜索时间模型。 The relevance of these combinations of features has been tested using linear regression. Models are built separately for each of the graphical models of the solvers. The features have been scaled to reduce their skewness and to equalise their magnitude, and a logarithmic transformation has been applied to the search time. All combinations of features are considered, and the best ones, determined using the adjusted R2 measure, are shown in Table II.
	Most models do not accurately predict the search times. The best model, corresponding to the primal constraint graph of the reductions of Choco, has an R2 value of only 0.5. At least one of the features related to the community structure is almost always included in the best models, however, which may be an indication of its importance. Other important features that are present in most models are the number of variables and constraints, the domain size and the average degree. The models corresponding to the reductions perform better in nearly all cases; a clear distinction between the graphical models is not obvious. The instances that could not be solved within the time limit of 30 minutes have a strong influence on the models, which can be seen in Figure 4 where these create the distinct pattern that is visible in the top right corner. Nonetheless, it appears that one or more important features are missing from these models. 译文：与约简对应的模型在几乎所有情况下都有较好的表现;图形模型之间的明显区别并不明显。在30分钟的时间限制内无法解决的实例对模型有很大的影响，可以在图4中看到，这些实例创建了在右上角可见的独特模式。尽管如此，这些模型似乎缺少一个或多个重要特征。
	Table II The included features and the adjusted R2 values for the best linear regression models for each combination of solver and graph type, for both types of problem instances: The complete and reduced version, encoded as C and R, respectively.

 

SECTION VII.

Correlation Between Modularity and Tree-Width

	Decomposition techniques, such as Tree-Decomposition, convert a CSP into a tree-like structure where the subtrees represent independent subproblems [22]. 译文：分解技术，如树分解，将CSP转换为树状结构，其中的子树表示独立的子问题[22]。 The tree-width captures how closely the tree decomposition resembles a tree, thereby providing information about the decomposability of the problem. 译文：树宽捕获了树分解与树的相似程度，从而提供了关于问题可分解性的信息。 These decomposition techniques directly manipulate the structure of a problem, which is, at least in part, characterised by the community structure. 译文：这些分解技术直接操纵问题的结构，至少部分地由社区结构来描述。
	To determine the influence of the community structure on the decomposability of a CSP and its relation to the tree-width, the instances of the reference set are decomposed using the Heuristic Tree-Decomposition without Triangulation algorithm [22]. 译文：为了确定社区结构对CSP可分解性的影响及其与树宽的关系，使用不带三角化算法[22]的启发式树分解方法对参考集实例进行分解。   The tree-width cannot easily be compared directly, however, as it is an absolute measure that partially depends on the size of the problem. 译文：然而，树宽不能简单地直接比较，因为它是一个绝对测量，部分取决于问题的大小。 Therefore, the ratio between the tree-width and the number of search variables is used, which gives a relative measure of the decomposability of a CSP. Only the full reductions are considered because the tree-decomposition of the full version of a FlatZinc instance virtually always has a tree-width that is higher than the number of search variables. 译文：因此，使用了树宽和搜索变量数量之间的比率，这给出了CSP可分解性的相对测度。只考虑完整的缩减，因为完整版本的FlatZinc实例的树分解实际上总是具有比搜索变量数量更高的树宽。 Additionally, as the algorithm performs decomposition directly on the variables, which corresponds to analysing the structure of the primal constraint graph, the community structure of the primal constraint graphs is used (the community structure of the other graphs has been investigated but did not show any interesting relations). 译文：此外，由于该算法直接对变量进行分解，对应于分析原约束图的结构，因此使用原约束图的团体结构(其他图的团体结构已经研究过，但没有显示出任何有趣的关系)。
	图4所示,与原始约束图的简化版本相对应的最佳choco线性回归模型的残差与拟合值。
	Figure 5 shows the relation between the modularity of the primal constraint graph and the ratio between the tree-width and the number of search variables. The ratio appears to decrease for higher values of the modularity, an indication that a stronger community structure corresponds to a better decomposition, although this trend becomes less apparent for higher values of the modularity. The modularity unmistakably separates the instances into two groups, however, where the ratio is close to 1.0 for instances for which the modularity is close to 0.0, and where the ratio is at most equal to 0.8 otherwise. Community structure seems to have a positive influence on the tree-decomposition, and decomposition techniques may, perhaps implicitly, make use of its existence. Incorporating decomposition techniques into general constraint solvers may allow those solvers to recognise these types of structures, possibly leading to improved performance.
	The tree-width also appears to be highly correlated with the maximum degree, the size of the largest constraint scope, as shown in Figure 6. 译文：树宽似乎也与最大程度高度相关，即最大约束范围的大小。For many instances, the maximum degree and the tree-width have equal values, and the tree-width of all other instances is higher than the maximum degree. The maximum degree seemingly serves as a good indicator of the tree-width, or at least as a lower bound on the tree-width. This correlation even persists after excluding the instances for which the modularity is close to zero or the ratio between the tree-width and the number of search variables is close to one. The maximum degree and the maximum community size, not included in this graph, also appear to be strongly correlated, which implies that the correlation between the tree-width and the maximum community size follows a similar trend.
	图5所示。树的宽度和绘制的搜索变量的数量之间的比率与模块化。
	Fig. 6. A visualisation of the correlation between the tree-width and the maximum degree.译文：树宽和最大程度之间的相关性的可视化。

SECTION VIII.

Conclusion & Future Work

	The structure of a CSP is an important characteristic with a potentially strong influence on the computational complexity of a problem. 译文：CSP的结构是影响问题计算复杂度的一个重要特征。 Community structure signifies an inherent partitioning of the variables and constraints, a type of structure that search algorithms may be able to exploit. 译文：社区结构表示变量和约束的固有划分，是搜索算法可以利用的一种结构类型。 An analysis of the community structure of the problem instances of the MiniZinc Challenge of 2019 shows that almost all instances exhibit strong community structure, albeit of varying degree, and that instances that belong to the same class have comparable community structure. 译文：对2019年MiniZinc挑战赛问题实例的社区结构分析表明，几乎所有实例都表现出较强的社区结构，尽管程度不同，属于同一类的实例具有可比较的社区结构。 As an independent feature, the community structure does not appear to be of great importance for explaining the differences in search time, but it has greater significance when combined into a linear model together with other features. 译文：社区结构作为一个独立的特征，对于解释搜索时间的差异似乎不是很重要，但当它与其他特征结合成一个线性模型时，具有更大的意义。 For Tree-Decomposition, on the other hand, the modularity is a reasonable predictor of the decomposability of a problem, at least for the full reductions. 译文：另一方面，对于树分解，模块化是一个合理的预测问题的可分解性，至少对于完全的约简。 Additionally, the tree-width shows a strong correlation with the maximum community size and the maximum degree, two features that are also mutually related. 译文：此外，树宽与最大群落大小和最大程度有较强的相关性，这两个特征也是相互关联的。
	For the solvers included in the experiments, the community structure only appears to have a marginal effect on the search time. 译文：对于实验中包含的求解器，社区结构对搜索时间的影响很小。 Determining to what extent it is possible for these solvers to take advantage of the community structure requires a more comprehensive analysis of the community structure. 译文：要确定这些求解器在多大程度上可以利用社区结构，需要对社区结构进行更全面的分析。 The community structure could potentially be used to define a new class of tractable problems as well, similar to the one defined for SAT problems. 译文：社区结构也可以用来定义一类新的可处理问题，类似于SAT问题的定义。 The relation between the tree-width and the community structure should also be investigated further to uncover possible cases where these two measures do not coincide. 译文：还应进一步研究树宽与群落结构之间的关系，以发现可能的情况下，这两个措施不一致。 In all of these cases, being able to generate problem instances with a known community structure may be valuable, as it allows for a more controlled way to examine the behaviour of different algorithms. 译文：在所有这些情况下，能够使用已知的社区结构生成问题实例可能是有价值的，因为它允许以一种更可控的方式来检查不同算法的行为。

References

1.V. Kumar, "Algorithms for Constraint-Satisfaction Problems: A Survey", AI Magazine, vol. 13, pp. 32, Mar. 1992.

 

2.C. Carbonnel and M. C. Cooper, "Tractability in constraint satisfaction problems: a survey", Constraints, vol. 21, pp. 115-144, Apr. 2016.

 

3.G. Gottlob, N. Leone and F. Scarcello, "A comparison of structural CSP decomposition methods", Artificial Intelligence, vol. 124, pp. 243-282, Dec. 2000.

 

4.P. Jegou, S. Ndiaye and C. Terrioux, Computing and exploiting tree-decomposition for (Max-)CSP, Jan. 2005.

 

5.R. Ganian and S. Szeider, "Community Structure Inspired Algorithms for SAT and #SAT", Theory and Applications of Satisfiability Testing – SAT 2015, vol. 9340, pp. 223-237, 2015.

 

6.C. Ansótegui, J. Giráldez-Cru and J. Levy, "The Community Structure of SAT Formulas", Theory and Applications of Satisfiability Testing – SAT 2012, vol. 7317, pp. 410-423, 2012.

 

7.R. Li, S. Hu and J. Wang, "The Community Structure of the Constraint Satisfaction Problem Instances of Model RB", Journal of Computational and Theoretical Nanoscience, vol. 12, pp. 6088-6093, Dec. 2015.

 

8.Z. Newsham, V. Ganesh, S. Fischmeister, G. Audemard and L. Simon, "Impact of Community Structure on SAT Solver Performance", Theory and Applications of Satisfiability Testing – SAT 2014, vol. 8561, pp. 252-268, 2014.

 

9.S. Fortunato, "Community detection in graphs", Physics Reports, vol. 486, pp. 75-174, Feb. 2010.

 

10.V. D. Blondel, J.-L. Guillaume, R. Lambiotte and E. Lefebvre, "Fast unfolding of communities in large networks", J. Stat. Mech., vol. 2008, pp. P10008, Oct. 2008.

 

11.M. J. Barber, "Modularity and community detection in bipartite networks", Phys. Rev. E, vol. 76, pp. 066102, Dec. 2007.

 

12.P. Jégou and C. Terrioux, "Hybrid backtracking bounded by tree-decomposition of constraint networks", Artificial Intelligence, vol. 146, pp. 43-75, May 2003.

 

13.M. C. Cooper and S. Zivny, "Hybrid Tractable Classes of Constraint Problems" in The Constraint Satisfaction Problem: Complexity and Approximability vol. 7 of Dagstuhl Follow-Ups, Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, pp. 113-135, 2017.

 

14.D. Marx, "Tractable Hypergraph Properties for Constraint Satisfaction and Conjunctive Queries", J. ACM, vol. 60, pp. 42:1-42:51, Nov. 2013.

 

15.C. Zhou, L. Feng and Q. Zhao, "A novel community detection method in bipartite networks", Physica A: Statistical Mechanics and its Applications, vol. 492, pp. 1679-1693, Feb. 2018.

 

16.P. J. Stuckey, T. Feydy, A. Schutt, G. Tack and J. Fischer, The MiniZinc Challenge 2008–2013, vol. 35, pp. 55-60, June 2014.

 

17.N. Nethercote, P. J. Stuckey, R. Becket, S. Brand, G. J. Duck and G. Tack, "MiniZinc: Towards a Standard CP Modelling Language", Principles and Practice of Constraint Programming – CP 2007, vol. 4741, pp. 529-543, 2007.

 

18.N. Jussien, G. Rochart and X. Lorca, "Choco: an Open Source Java Constraint Programming Library", CPAIOR'08 Workshop on Open-Source Software for Integer and Contraint Programming (OSSICP'08), pp. 1-10, 2008.

 

19.OR-Tools ∣ Google Developers, [online] Available: https://developers.google.com/.

 

20.GECODE - An open free efficient constraint solving toolkit.

 

21.C. Geoffrey, P. J. Stuckey, A. Schutt, T. Ehlers, G. Gange and K. Francis, Chuffed, Apr. 2020, [online] Available: https://github.com/chuffed/chuffed.

 

22.P. Jégou, H. Kanso and C. Terrioux, "An Algorithmic Framework for Decomposing Constraint Networks", 2015 IEEE 27th International Conference on Tools with Artificial Intelligence (ICTAI), pp. 1-8, 2015.