文献信息
- Knot Pipatsrisawat, Adnan Darwiche:
A New Clause Learning Scheme for Efficient Unsatisfiability Proofs. AAAI 2008: 1481-1484 - http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.333.1891&rep=rep1&type=pdf
- http://reasoning.cs.ucla.edu/rsat/index.html --该主页提供源代码下载,时至今日仍有借鉴的地方。
- RSat is a complete Boolean satisfiability solver with an exhaustive search interface for applications such as model counting and knowledge compilation. RSat uses a phase selection heuristic that is oriented toward reducing work repetition and a frequent restart policy.
本文给出了许多概念:
- asserting clauses
- empowerment--we formalize an essential property of asserting clauses
- 1–inconsistent
- 1–Empowerment
Note that if a clause is not 1–empowering with respect to a knowledge base, adding more clauses to the knowledge base will not make it so.
- Bi-Asserting Clause
- 1–Empowering Bi-Asserting Clauses
- n intermediate conflict clause
| Abstract | |
| We formalize in this paper a key property of asserting clauses (the most common type of clauses learned by SAT solvers). We show that the formalized property, which is called empowerment, is not exclusive to asserting clauses, and introduce a new class of learned clauses which can also be empowering. We show empirically that (1) the new class of clauses tends to be much shorter and induce further backtracks than asserting clauses and (2) an empowering subset of this new class of clauses significantly improves the performance of the Rsat solver on unsatisfiable problems. | |
| Introduction | |
| An important technique that underlies most modern SAT solvers is conflict-clause learning (Marques-Silva and Sakallah 1996). The algorithm for deriving conflict clauses in these SAT solvers is based on using implication graphs to derive a particular class of conflict clauses known as asserting clauses (Marques-Silva and Sakallah 1996; Moskewicz et al. 2001). | |
| In this paper, we formalize an essential property of asserting clauses, which may also be satisfied by some non-asserting clauses. | |
| We then define a new class of clauses which is a relaxation of asserting clauses and show that they tend to be shorter than asserting clauses and lead to much further backtracks. | |
| Empirical results show that selectively learning the new type of clauses significantly improves the performance of Rsat, the winner of the industrial category of the SAT’07 competition, on unsatisfiable problems. | |
| We begin the next section by presenting a model of modern clause-learning SAT solvers, which we use as a basis for our discussions in this paper. | |
| Then, we introduce a property of conflict clauses, called empowerment(赋权). Next, we define a new class of conflict clauses and present an efficient algorithm for deriving them. | |
|
Then, we discuss a special subset of this new class which satisfies empowerment. 译文:然后,我们讨论了这个新类的一个满足授权的特殊子集。 Finally, we present experimental results and end with conclusions. Proofs of all propositions in this paper can be found in (Pipatsrisawat and Darwiche 2008). |
|
| A Model of Modern SAT Solvers | |
 |
|
entailvt. 使需要,必需;承担;遗传给;蕴含 n. 引起;需要;继承
are checked for inconsistency using unit resolution 译文:使用单元归结检查不一致。
• If the decision sequence is empty, the CNF ∆ must be unsatisfiable and the algorithm terminates (Line 4). • If the decision sequence is not empty, an asserting clause α is generated with an assertion level m. The algorithm then erases all decisions made after level m, adds α to Γ, and moves on to the next iteration (Lines 5-8). 译文:如果决策序列不为空,则生成断言子句α,其断言级别为m,然后算法删除所有在m级之后做出的决策。
If unit resolution detects no inconsistency, the algorithm tries to find a literal ℓ whose value is not currently implied or falsified by unit resolution, and adds it to the decision sequence (Line 12).译文:如果单元解析没有检测到不一致,算法将尝试找到一个文本ℓ,其值当前没有被单元解析隐含或篡改,并将其添加到决策序列中(第12行)。
When appropriate, we will treat a decision sequence as the conjunction or the set of all literals in the sequence。译文:在适当的时候,我们将把决策序列看作序列中所有文字的合取或集合。
|
|
|
Definition 1 (Conflict Clause) An asserting clause is a special type of conflict clause that satisfies some strong conditions, so we start first by defining the weaker notion of a conflict clause.译文:断言条款是满足强条件的一种特殊类型的冲突条款,因此我们首先定义冲突条款的弱概念。
Every conflict clause must contain at least one literal that is falsified in the last level. Otherwise, the SAT state would not be normal, because the previous state must be 1–inconsistent. In practice, however, modern SAT solvers insist on learning conflict clauses that contain exactly one literal falsified in the last level. 译文: |
|
|
Definition 2 (Asserting Clause)
An asserting clause is guaranteed to become unit once the solver backtracks to the assertion level. Moreover, an asserting clause can always be derived for a 1–inconsistent SAT state that has at least one decision.译文:一旦求解器回溯到断言级别,断言子句保证成为单元。而且,对于至少有一个决定的1 -不一致SAT状态,总是可以派生断言子句。 |
|
|
The completeness of Algorithm 1 can be shown by realizing that asserting clauses learned by the algorithm never repeat (otherwise, the conflict would have been prevented).译文:算法1的完整性可以通过实现算法学到的断言子句永远不会重复(否则,冲突就会被防止)来显示。 Since every conflict comes with an asserting clause (Proposition 1) and there are only finitely many clauses, the algorithm can only experience a finite number of conflicts. 译文:由于每个冲突都有一个断言子句(命题1),且子句数量有限,算法只能经历有限数量的冲突。It cannot keep making decisions indefinitely either and, therefore, has to terminate. This proof will be referred to again when we introduce a new class of conflict clauses.译文:它也不能无限期地做决定,因此必须终止。当我们引入一类新的冲突条款时,我们将再次引用这个证明。 |
|
| Empowerment | |
|
|
|
|
This means that adding a conflict clause that is not 1– empowering to the knowledge base will not lead to any new implication. Note that if a clause is not 1–empowering with respect to a knowledge base, adding more clauses to the knowledge base will not make it so. 译文:这意味着添加一个不是1-授权给知识库的冲突子句不会导致任何新的蕴含。请注意,如果一个子句对于知识库不是1授权的,那么向知识库添加更多子句并不会使它成为1授权。 |
|
|
Proposition 2 All asserting clauses of a SAT state S are 1– empowering with respect to S and the asserted literals are their empowering literals. |
|
|
Given this result, the learning component of Algorithm 1 can be viewed as one that tries to empower unit resolution so that it becomes more complete.译文:考虑到这个结果,算法1的学习部分可以被看作是试图增强单元分辨率,使其变得更完整。 In particular, each time unit resolution discovers a contradiction, it does so under a particular decision sequence.译文:特别是,每次时间单元解析发现一个矛盾,它是在一个特定的决策序列下这样做的。 When this sequence is not empty, it means that unit resolution has missed an implication due to its incompleteness.译文:当这个序列不为空时,就意味着单元解析由于不完整而错过了一个含义。 By adding the empowering clause, we are effectively allowing unit resolution to discover this implication at an earlier stage, using only part of the current decision sequence.译文:通过添加授权条款,我们有效地允许单元决议在早期阶段发现这一含义,只使用当前决策序列的一部分。 Therefore, the shorter the empowering clause is, the better it is in making unit resolution more complete. 译文:因此,授权条款越短,越有利于使单位决议更加完整。 Moreover, an empowering clause with a smaller assertion level will allow unit resolution to derive the missed implication under a smaller subset of the current decision sequence。译文:此外,具有较小断言级别的授权子句将允许单元解析在当前决策序列的较小子集下推导出遗漏的含义。 |
|
| A New Class of Conflict Clauses | |
|
In this section, we introduce a new class of clauses, which is a relaxation of asserting clauses. This class of clauses may satisfy the empowerment property as well. Later, we argue and show empirically that an empowering subset of this new class could improve the performance of SAT solvers. 译文:之后,我们讨论并实证地证明了这个新类的强大子集可以提高SAT求解器的性能。 |
|
|
译文:β的断言级别被定义为其字面量的第二高隐含级别。如果|β| = 2,则定义其断言级别为零。 |
|
|
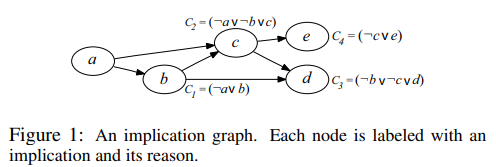
Let ∆ be the conjunction of C1 = (¬a ∨ b), C2 = (¬a ∨ ¬b ∨ c), C3 = (¬b ∨ ¬c ∨ d), C4 = (¬c∨e), C5 = (¬d∨ ¬e). Now, consider the state S = (∆, true,hai). From this state, unit resolution will derive some implications before discovering a conflict. The derivations of implications are visualized in Figure 1.
An edge X → Y in this graph indicates that X’s literal directly contributes to the implication of Y ’s. A reason of an implication is the clause in which the literal becomes unit. In this case, assume that the implications b, c, d, e are discovered in this order and that C5 is found to be empty (all of its literals have been falsified). The following trace shows how Algorithm 2 derives an asserting clause from this example 。 |
|
|
The algorithm starts by initializing the conflict clause to be the empty clause (Step 1). Then, it picks a literal in the clause whose negation was implied last (e in this case). The algorithm resolves the reason of this literal (Step 2) with the conflict clause and replaces the conflict clause with the resolvent, (¬c ∨ ¬d) (Step 3). Next, since, in the current conflict clause, the negation of ¬d was implied last, the algorithm resolves its reason (Step 4) with the conflict clause and produces (¬b ∨ ¬c) (Step 5). This process is repeated until the conflict clause becomes asserting (Step 9). We refer to the clauses in Steps 3,5,7 as intermediate conflict clauses. 译文:这个过程不断重复,直到冲突子句成为断言(步骤9)。我们将步骤3,5,7中的子句称为中间冲突子句。 |
|
|
This algorithm can be modified to derive bi-asserting clauses without any added complexity.译文:该算法可以在不增加任何复杂性的情况下推导双断言子句。 We only need to detect when the intermediate conflict clause contains two (instead of one) literals falsified at the conflict level. 译文:我们只需要检测中间冲突子句是否包含在冲突级别伪造的两个(而不是一个)字面量。 Note, however, that not every bi-asserting clause is 1–empowering and the algorithm described above, does not guarantee to produce 1–empowering bi-asserting clauses. 译文:但是请注意,并不是每个双断言子句都是1授权的,而且上面描述的算法并不保证生成1授权的双断言子句。 For example, the bi-asserting clause (¬c ∨ ¬d) is not 1–empowering for the above example, while (¬b∨¬c) is. This suggests that biasserting clauses should be learned with care to avoid adding clauses that will not contribute any new implication. 译文:这表明,应该小心地学习双断言从句,以避免添加不会产生任何新含义的从句。 |
|
|
Learning 1–Empowering Bi-Asserting Clauses |
|
|
In this section, we address the issue of learning 1– empowering bi-asserting clauses. In general, checking whether the clause α ⇒ ℓ is empowering with respect to CNF ∆ via literal ℓ can be done by checking if ∆ ∧ ¬α ⊢ ℓ. The time complexity of this test is linear in the size of the knowledge base. In practice, however, this test would incur too much overhead. Hence, we will next present an efficient algorithm that detects the empowerment of the derived bi-asserting clause, but only with respect to the clauses used in its derivation.译文:因此,我们接下来将提出一种有效的算法,检测派生的双断言子句的授权,但仅针对其派生中使用的子句。 Even though the derived bi-asserting clauses are not guaranteed to be 1–empowering with respect to other clauses in the knowledge base, we will show in the next section that they tend to in the majority of cases.译文:尽管派生的双断言子句并不保证与知识库中的其他子句相比具有1权,但在下一节中,我们将展示在大多数情况下它们倾向于这样做。
Our approach for generating empowering bi-asserting clauses is based on the notions of merge resolutions. 译文:我们生成增强功能的双断言子句的方法基于合并解析的概念。 Defined in (Andrews 1968), a resolution between clauses C1 and C2 is a merge resolution iff C1 and C2 share a literal (C1∩C2 != ∅).
|
|
|
Proposition 3 An intermediate conflict clause of Algorithm 2 is 1–empowering with respect to the clauses used in its derivation if at least a step in the derivation is a merge resolution. 译文:如果算法2的中间冲突子句中至少有一个步骤是合并解析,则该子句相对于其派生过程中使用的子句具有1权。
Based on this result, all we need to ensure that the conflict clause is 1–empowering is the existence of a single merge resolution step in the resolution derivation of the clause. This additional check incurs very little overhead.译文:在这个结果的基础上,我们需要确保冲突子句是1授权的,只需要在子句的解析派生中存在一个单独的合并解析步骤。这种额外的检查产生的开销很小。 We close this section by noting that integrating biasserting clauses into Algorithm 1 still maintains the completeness of the algorithm given that a standard unit propagation algorithm is used (Ryan 2004). 译文:我们在结束这一节时注意到,在算法1中集成双断言子句仍然保持了算法的完整性,前提是使用了标准单元传播算法(Ryan 2004)。 This is due to the result in (Ryan 2004), which states that every intermediate conflict clause in the derivation must not already appear in the knowledge base at the time of the derivation. As a result, our completeness proof presented earlier still holds.译文:这是由于(Ryan 2004)中的结果,该结果指出,推导过程中的每个中间冲突子句在推导时都不能已经出现在知识库中。因此,我们之前提出的完整性证明仍然成立。 |
|
| Experimental Results | |
|
We modified Rsat (Pipatsrisawat and Darwiche 2007), the winner of the SAT’07 competition (industrial category), to detect any occurrence of 1–empowering bi-asserting clauses (with respect to the clauses in the derivation) during conflict clause derivation.译文:我们修改了SAT ' 07竞赛(工业类别)的获胜者Rsat (Pipatsrisawat and Darwiche 2007),以检测在冲突条款推导过程中出现的任何1 -授权双断言条款(与推导中的条款相关)。
If found, the bi-asserting clause is learned instead of the asserting clause otherwise learned. We considered Rsat with the following learning schemes: (i) learn only asserting clauses (normal Rsat) (ii) learn 1– empowering bi-asserting clause when possible (Rsat+) (iii) learns 1–empowering bi-asserting clause only when its assertion level is at least 2 levels smaller than that of the asserting clause (Rsat++). 译文:双断言子句被学习而不是断言子句被学习。 三种情况做对比:
译文:(i)只学习断言子句(普通Rsat)。 (ii) learn 1– empowering bi-asserting clause when possible (Rsat+);1-授权双断言子句尽可都被学习。 译文:(iii)只有当断言级别比断言子句至少小2个级别时,才能学习1授权的双断言子句(Rsat++)。 |
|
|
Although empowerment is only with respect to the clauses used in the derivation, in practice, it usually results in empowerment with respect to the whole formula.译文:虽然授权仅涉及推导中使用的条款,但在实践中,它通常导致授权涉及整个公式。 We found that, on 95% of the problems, over 80% of the bi-asserting clauses derived are 1–empowering with respect to the whole formula at the time of learning.译文:我们发现,在95%的问题上,超过80%的双断言子句在学习时对整个公式赋1权。 |
|
|
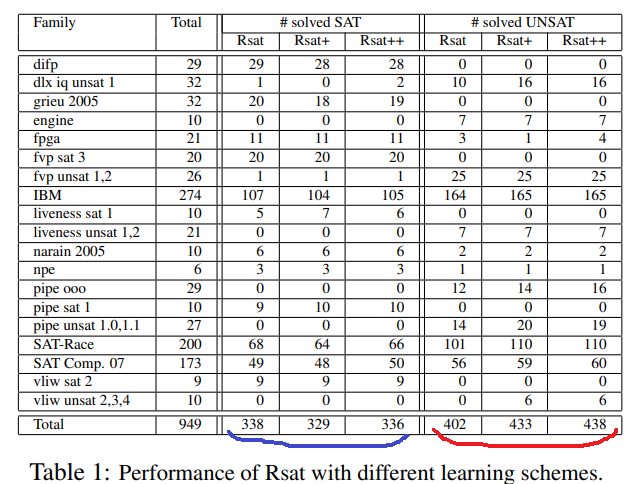
We experimented with 949 SAT problems from previous SAT/SAT-Race competitions and contemporary libraries.2 Each solver is given 1,800 seconds per problem on a 3.8GHz machine with 3GB of RAM. Table 1 reports the number of problems solved by different versions. According to this table, Rsat+ and Rsat++ perform considerably better than Rsat. For satisfiable problems, Rsat+ tends to be worse than the others, whereas Rsat and Rsat++ have comparable performances. For unsatisfiable problems, however, Rsat++ and Rsat+ solve 36 and 31 more problems than Rsat, respectively. Moreover, the new learning scheme decreases the running time on unsatisfiable problems by 34% (71,246 s for Rsat and 47,400 s for Rsat++). Overall, Rsat++ used only 99,209 seconds, while Rsat used 114,600 seconds.
|
|
|
We have also evaluated the version of Rsat that learns biasserting clauses regardless of their empowerment. This version of Rsat solved only 647 problems (normal Rsat solved 740 problems). This is because these bi-asserting clauses are not necessarily capable of generating any new implications. So, in the long run, they only contribute to the overhead of unit propagation no matter how short they are.
We also measured the sizes of different conflict clauses derived by Rsat++ and found that, on average, the size of a bi-asserting clause is slightly less than half the size of an asserting clause. Moreover, on average, the backtrack induced by a bi-asserting clause is about 5-6 times longer than the one induced by an asserting clause. |
|
| Related Work and Conclusions | |
|
Learning non-asserting clauses have been previously proposed by (Ryan 2004) and (Dershowitz, Hanna, and Nadel 2007). In both work, non-asserting clauses are learned in addition to asserting clauses (i.e. the solvers may add two clauses per conflict). Moreover, additional clauses learned in both cases may not be empowering nor bi-asserting.译文:此外,在这两种情况下学到的附加条款可能既没有授权也没有双重主张。
In conclusion, we formalized a key property of asserting clauses called empowerment and presented a new class of conflict clauses called bi-asserting clauses. Our experiments showed that, by selectively learning empowering biasserting clauses, Rsat produces shorter conflict clauses, performs longer backtracks, and performs better on unsatisfiable problems.译文:我们的实验表明,通过选择性地学习双断言子句,Rsat产生更短的冲突子句,执行更长的回溯,并在不满意的问题上表现得更好。 |
|
|
References Andrews, P. B. 1968. Resolution with merging. J. ACM 15(3):367–381. del Val, A. 1994. Tractable databases: How to make propositional unit resolution complete through compilation. In Proceedings of KR-94, pp. 551-561. Dershowitz, N.; Hanna, Z.; and Nadel, A. 2007. Towards a better understanding of the functionality of a conflictdriven sat solver. In SAT, 287–293. Een, N., and S ´ orensson, N. 2003. An extensible sat-solver. ¨ In Proceedings of SAT 2003. Marques-Silva, J. P., and Sakallah, K. A. 1996. GRASP - A New Search Algorithm for Satisfiability. In Proceedings of IEEE/ACM Intl. Conf. on CAD, 220–227. Moskewicz, M.; Madigan, C.; Zhao, Y.; Zhang, L.; and Malik, S. 2001. Chaff: Engineering an efficient sat solver. In Proceedings of DAC’01, June 2001. Pipatsrisawat, K., and Darwiche, A. 2007. Rsat 2.0: Sat solver description. Technical Report D–153, Automated Reasoning Group, Comp. Sci. Department, UCLA. Pipatsrisawat, K., and Darwiche, A. 2008. A new clause learning scheme for efficient unsatisfiability proofs. Technical Report D–156, Automated Reasoning Group, Comp. Sci. Department, UCLA. Ryan, L. 2004. Efficient Algorithms for Clause-Learning SAT Solvers. Master’s thesis, Simon Fraser University. Zhang, L.; Madigan, C. F.; Moskewicz, M. W.; and Malik, S. 2001. Efficient conflict driven learning in boolean satisfiability solver. In ICCAD-01, 279–285. |
|