Machine Learning-Based Restart Policy for CDCL SAT Solvers
阅读注释:提出运用之前学习的子句的历史预测下一个学习的子句的质量。
Liang J.H., Oh C., Mathew M., Thomas C., Li C., Ganesh V. (2018) Machine Learning-Based Restart Policy for CDCL SAT Solvers. In: Beyersdorff O., Wintersteiger C. (eds) Theory and Applications of Satisfiability Testing – SAT 2018. SAT 2018. Lecture Notes in Computer Science, vol 10929. Springer, Cham. https://doi.org/10.1007/978-3-319-94144-8_6
Abstract
|
Restarts are a critically important heuristic in most modern conflict-driven clause-learning (CDCL) SAT solvers. The precise reason as to why and how restarts enable CDCL solvers to scale efficiently remains obscure. In this paper we address this question, and provide some answers that enabled us to design a new effective machine learning-based restart policy. 译文:在本文中,我们解决了这个问题,并提供了一些答案,使我们能够设计一个新的有效的基于机器学习的重启策略。
Specifically, we provide evidence that restarts improve the quality of learnt clauses as measured by one of best known clause quality metrics, namely, literal block distance (LBD). More precisely, we show that more frequent restarts decrease the LBD of learnt clauses, which in turn improves solver performance.
We also note that too many restarts can be harmful because of the computational overhead of rebuilding the search tree from scratch too frequently.译文:我们还注意到,过多的重新启动可能是有害的,因为过于频繁地从头开始重建搜索树会带来计算开销。 With this trade-off in mind, between that of learning better clauses vs. the computational overhead of rebuilding the search tree, we introduce a new machine learning-based restart policy that predicts the quality of the next learnt clause based on the history of previously learnt clauses.译文:考虑到这种权衡,在学习更好的子句与重建搜索树的计算开销之间,我们引入了一种新的基于机器学习的重启策略,该策略基于之前学习的子句的历史预测下一个学习的子句的质量。
The restart policy erases the solver’s search tree during its run, if it predicts that the quality of the next learnt clause is below some dynamic threshold that is determined by the solver’s history on the given input.译文:如果它预测下一个学习到的子句的质量低于某个由求解器对给定输入的历史决定的动态阈值,重启策略在运行过程中删除求解程序的搜索树。
Our machine learning-based restart policy is based on two observations gleaned from our study of LBDs of learnt clauses.译文:我们基于机器学习的重启策略是基于我们对已学习语句的lbd研究中收集到的两种观察结果。 First, we discover that high LBD percentiles can be approximated with z-scores of the normal distribution. 译文:我们发现高的LBD百分位数可以用正态分布的z分数来近似。 Second, we find that LBDs, viewed as a sequence, are correlated and hence the LBDs of past learnt clauses can be used to predict the LBD of future ones.译文:其次,我们发现,从一个序列上看,过去习得从句的LBD是相互关联的,因此可以用过去习得从句的LBD来预测未来从句的LBD。
With these observations in place, and techniques to exploit them, our new restart policy is shown to be effective over a large benchmark from the SAT Competition 2014 to 2017.译文:有了这些观察结果,以及利用它们的技术,我们新的重启政策在2014年到2017年的SAT考试中被证明是有效的。 |
|
1 Introduction
|
The Boolean satisfiability problem is a fundamental problem in computer science: given a Boolean formula in conjunctive normal form, does there exist an assignment to the Boolean variables such that the formula evaluates to true? Boolean satisfiability is the quintessential NP-complete [13] problem, and hence one might prematurely conjecture that Boolean SAT solvers cannot scale. Yet modern SAT solvers routinely solve instances with millions of Boolean variables. In practice, many practitioners reduce a variety of NP problems to the Boolean satisfiability problem, and simply call a modern SAT solver as a black box to efficiently find a solution to their problem instance [11, 12, 19]. For precisely this reason, SAT solving has become an important tool for many industrial applications. Through decades of research, the SAT community has built surprisingly effective backtracking solvers called conflict-driven clause-learning (CDCL) [23] SAT solvers that are based on just a handful of key principles [18]: conflict-driven branching, efficient propagation, conflict analysis, preprocessing/inprocessing, and restarts.译文:通过几十年的研究,SAT社区已经建立了令人惊讶的有效回溯解决程序称为冲突驱动子句学习(CDCL) [23] SAT解决程序,这是基于一些关键原则[18]:冲突驱动分支,高效传播,冲突分析,预处理/处理中,和重启。 |
|
|
Like all backtracking search, the run of a CDCL SAT solver can be visualized as a search tree where each distinct variable is a node with two outgoing edges marked true and false (denoting value assignments to the variable) respectively. The solver frequently restarts, that is, it discards the current search tree and begins anew (but does not throw away the learnt clauses and the variable activities).译文:求解器经常重新启动,也就是说,它丢弃当前的搜索树并重新开始(但不丢弃已学习的子句和可变活动)。 Although this may seem counterproductive, SAT solvers that restart frequently are significantly faster empirically than solvers that opt not to restart. The connection between restarts and performance is not entirely clear, although researchers have proposed a variety of hypotheses such as exploiting variance in the runtime distribution [14, 22] (similar to certain kinds of randomized algorithms).译文:重启和性能之间的关系并不完全清楚,尽管研究人员提出了各种假设,如利用运行时分布中的方差[14,22](类似于某些随机算法)。
For various reasons however, we find these hypotheses do not explain the power of restarts in the CDCL SAT solver setting. 译文:然而,由于种种原因,我们发现这些假设并不能解释在CDCL SAT求解器设置中重启的力量。 In this paper, we take inspiration from Hamadi et al. who claim that the purpose of restarts is to compact the assignment stack [16].译文:本文借鉴了haadi等人的观点,他们认为重启的目的是为了压缩分配堆栈[16]。 We then further show that a compact stack tends to improve the quality of clauses learnt where we define quality in terms of the well-known metric literal block distance (LBD).译文:然后,我们进一步表明,紧凑堆栈倾向于提高学习到的子句的质量,我们根据众所周知的度量文字块距离(LBD)来定义质量。 Despite the search tree being discarded by a restart, learnt clauses are preserved so learning higher quality clauses continues to reap benefits across restarts.译文:尽管重新开始时搜索树被丢弃,但已学习的子句被保留下来,因此学习更高质量的子句继续在重新开始时获得好处。 By learning higher quality clauses, the solver tends to find a solution quicker. However, restarting too often incurs a high overhead of constantly rebuilding the search tree. So it is imperative to balance the restart frequency to improve the LBD but avoid excessive overhead.译文:通过学习高质量的条款,求解者往往会更快地找到解决方案。然而,频繁重启会导致不断重建搜索树的高开销。因此,必须平衡重启频率,以提高LBD,同时避免过多的开销。 |
|
|
Based on the above-mentioned analysis, we designed a new restart policy called machine learning-based restart (MLR) that triggers a restart when the LBD of the next learnt clause is above a certain threshold. The motivation for this policy is that rather than investing computation into learning a low quality clause, the solver should invest that time in rebuilding the search tree instead in the hopes of learning a better clause.译文:这个策略的动机是,与其把计算花费在学习低质量的子句上,求解器应该把时间花在重建搜索树上,而不是希望学习一个更好的子句。
This restart policy is based on two key observations that we made by analyzing CDCL solvers over a large benchmark: First, we observed that recent LBDs are correlated with the next LBD. 译文:首先,我们观察到最近的LBD与下一个LBD相关。We introduce a machine learning-based technique exploiting this observation to predict the LBD of the next learnt clause. 译文:我们介绍了一种基于机器学习的技术,利用这种观察来预测下一个学习的小句的LBD。 Second, we observed that the right tail of the LBD distribution is similar to the right tail of the normal distribution.译文:我们观察到LBD分布的右尾部与正态分布的右尾部相似。 We exploit this observation to set a meaningful LBD threshold for MLR based on percentiles. 译文:我们利用这一观察结果,基于百分位为MLR设置一个有意义的LBD阈值。 MLR is then shown to be competitive vis-a-vis the current state-of-the-art restart policy implemented as part of the Glucose solver [4]. |
|
| Contributions: We make the following contributions in this paper: | |
| 1.
We provide experimental support for the hypothesis that restarts “compact the assignment stack” as stated by the authors of ManySAT [16] (see Sect. 4). We then add to this hypothesis, and go on to show that a compact assignment stack correlates with learning lower LBD clauses (see Sect. 4.2). Lastly, learning clauses with lower LBD is shown to correlate with better solving time (see Sect. 4.3). Additionally we provide analytical explanations as to why we discount some previously proposed hypotheses that attempt to explain the power of restarts in practice (see Sect. 3). |
|
|
2. We propose a method to set thresholds for the quality of a LBD of a clause. We experimentally show that the right tail of the LBD distribution closely matches a normal distribution, hence high percentiles can be accurately predicted by simply computing the mean and standard deviation. See Sect. 5.1 for details. |
|
|
3. We show that LBDs viewed as a sequence are correlated. This is a crucial observation that we back by experimental data. The fact that LBDs viewed as a sequence are correlated enables us to take the LBDs of recent learnt clauses and predict the LBD of the next clause. See Sect. 5.2 for details. |
|
| 4.
Building on all the above-mentioned experimentally-verified observations, we introduce a new restart policy called machine learning-based restart (MLR) that is competitive vis-a-vis the current state-of-the-art restart policy on a comprehensive benchmark from the SAT Competition 2014 to 2017 instances. See Sect. 6 for details. |
|
2 Background
| We assume the reader is familiar with the Boolean satisfiability problem and SAT solver research literature [6]. | |
| LBD Clause Quality Metric: | |
|
It has been shown, through the lens of proof complexity, that clause-learning SAT solvers (under perfect non-deterministic branching and restarts, and asserting clause learning schemes) are exponentially more powerful than CDCL SAT solvers without clause learning [26]. However, the memory requirement to store all the learnt clauses is too high for many instances since the number of conflicts grows very rapidly. To overcome this issue, all modern SAT solvers routinely delete some clauses to manage the memory usage. The most popular metric to measure the quality of a clause is called literal block distance (LBD) [3], defined as the number of distinct decision levels of the variables in the clause. Intuitively, a clause with low LBD prunes more search space than a clause with higher LBD. Hence clauses with high LBD typically are the ones prioritized for deletion. Although LBD was originally proposed for the purpose of clause deletion, it has since proven useful in other contexts where there is need to measure the quality of learnt clauses such as sharing clauses in parallel SAT solvers and restarts. Another measure of quality of a learnt clause is its length. To the best of our knowledge, we are not aware of any other universally accepted clause quality metrics at the time of writing of this paper. |
|
| In this paper we will often look at LBDs as a sequence. At any time during the search where i conflicts have occurred, we use the term “previous” LBD to refer to the LBD of the clause learnt at the ithith conflict and “next” LBD to refer to the LBD of the clause learnt at the (i+1)th conflict. | |
|
Overview of Restarts in CDCL SAT Solvers: Informally, a restart heuristic in the context of CDCL SAT solver can be defined as a method that discards parts of the solver state at certain points in time during its run. CDCL solvers restart by discarding their “current” partial assignment and starting the search over, but all other aspects of solver state (namely, the learnt clauses, variable activities, and variable phases) are preserved. 译文:CDCL求解器通过丢弃其“当前”部分赋值并重新开始搜索来重新启动,但求解器状态的所有其他方面(即已学习的子句、变量活动和变量阶段)都被保留。 Although restarts may appear unintuitive, the fact that learnt clauses are preserved means that solver continues to make progress. Restarts are implemented in practically all modern CDCL solvers because it is well known that frequent restarts greatly improve solver performance in practice. |
|
|
|
3 Prior Hypotheses on “The Power of Restarts”
| In this section, we discuss prior hypotheses on the power of restarts in the DPLL and local search setting and their connection to restarts in the CDCL setting. | |
4 “Restarts Enable Learning Better Clauses” Hypothesis
|
In this section, we propose that restarts enable a CDCL solver to learn better clauses. To justify our hypothesis, we start by examining the claim by Hamadi et al. [16] stating that “In SAT, restarts policies are used to compact the assignment stack and improve the order of assumptions.” 译文:在本节中,我们建议通过重启使CDCL求解器能够学习更好的子句。为了证明我们的假设,我们首先检查Hamadi等人[16]的声明:“在SAT中,重启策略用于压缩分配堆栈,改善假设的顺序。”
Recall that in CDCL SAT solvers, the only thing that changes during a restart is the assignment stack, and hence the benefits of restarts should be observable on the assignment stack. In this paper, we show that this claim matches reality, that is, restarting frequently correlates with a smaller assignment stack. We then go one step further, and show that a compact assignment stack leads to better clause learning.
That is, the solver ends up learning clauses with lower LBD, thereby supporting our hypothesis, and this in turn improves the solver performance. |
|
5 A Machine Learning-Based Restart Policy
|
In this section, we describe our machine learning-based restart policy. 译文:我们描述了基于机器学习的重启策略 We first start by answering the two questions posed in the last subsection regarding LBD percentile and predicting LBD of the next clause.译文:我们首先回答上一小节中提出的关于LBD百分位数和预测下一个从句的LBD的两个问题 |
|
5.1 LBD Percentile |
|
|
Given the LBD of a clause, it is unclear a priori how to label it as “good” or “bad”. Some heuristics set a constant threshold and any LBDs above this threshold are considered bad. 译文:考虑到一个条款的LBD,如何给它贴上“好”或“坏”的标签是一个先验的不清楚的问题。一些启发式方法设置了一个恒定的阈值,超过这个阈值的任何lbd都被认为是不好的。 For example, Plingeling [7] considers learnt clauses with LBD greater 7 to be bad, and these clauses are not shared with the other workers. COMiniSatPS considers learnt clauses with LBD greater than 8 to be bad, and hence these clauses are readily deleted [25]. The state-of-the-art Glucose restart policy [4] on the other hand uses the mean LBD multiplied by a fixed constant as a threshold.译文:另一方面,最先进的血糖恢复策略[4]使用平均LBD乘以一个固定常数作为阈值。 The problem with using a fixed constant or the mean times a constant for thresholds is that we do not have a priori estimate of how many clauses exceed this threshold, and these thresholds seem arbitrary. 译文:使用固定常数或平均值乘以常数作为阈值的问题是,我们没有先验估计有多少子句超过这个阈值,而且这些阈值似乎是任意的。 Using arbitrary thresholds makes it harder to reason about solver heuristics, and in this context, the efficacy of restart policies.译文:使用任意阈值会使求解器启发式推理变得更加困难,在这种情况下,重启策略的有效性也变得更加困难。 |
|
|
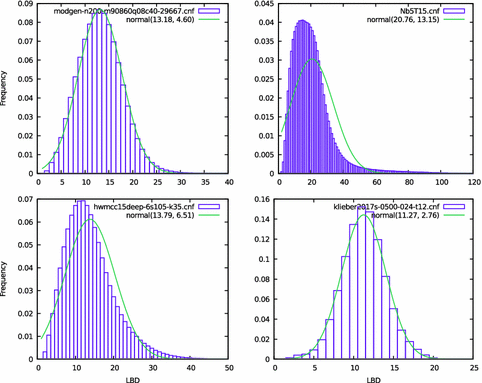
We instead propose that for any given input it is more appropriate to use dynamic threshold that is computed based on the history of the CDCL solver’s run on that input.译文:相反,我们建议,对于任何给定的输入,使用基于CDCL求解器在该输入上运行的历史计算的动态阈值更为合适。 At any point in time during the run of the solver, the dynamic threshold is computed as the 99.9th percentile of LBDs of the learnt clauses seen during the run so far.译文:在求解器运行期间的任何时间点,动态阈值将计算为迄今为止在运行期间看到的已学习的子句的99.9百分位lbd。 Before we estimate whether an LBD is in the 99.9th percentile, the first step is to analyze the distribution of LBDs seen in practice. In this experiment, the Glucose solver was run on all 350 instances in SAT Competition 2017 main track for 30 min and the LBDs of all the learnt clauses were recorded.译文:在本次实验中,我们在2017年SAT竞赛主赛道的所有350个实例上运行葡萄糖求解器30分钟,记录所有学习到的子句的lbd。 Figure 5 shows the histogram of LBDs for 4 representative instances. As can be seen from the distributions of these representative instances, either their LBD distribution is close to normal or a right-skewed one.译文:从这些代表性实例的分布可以看出,它们的LBD分布要么接近正态分布,要么是右偏态分布。 |
|
|
Fig. 5. Histogram of LBDs of 4 instances. A normal distribution with the same mean and variance is overlaid on top for comparison.
|
|
|
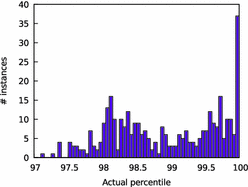
Even though the right-skew distribution is not normal, the high percentiles can still be approximated by the normal distribution since the right tail is close to the normal curve. 译文:即使右斜分布不是正态分布,高百分位数仍然可以近似于正态分布,因为右尾部接近于正态曲线。We conducted the following experiment to support this claim. For each instance, we computed the mean and variance of the LBD distribution to draw a normal distribution with the same mean and variance.译文:为了支持这一说法,我们进行了下面的实验。对于每个实例,我们计算LBD分布的均值和方差,以绘制具有相同均值和方差的正态分布。 We used the normal distribution to predict the LBD x at the 99.9th percentile. 译文:我们使用正态分布来预测99.9百分位的LBD x。We then checked the recorded LBD distribution to see the actual percentile of x. 译文:然后我们检查记录的LBD分布,以查看x的实际百分位数。 Figure 6 is a histogram of all the actual percentiles. Even in the worst case, the predicted 99.9th percentile turned out to be the 97.1th percentile. Hence for this benchmark the prediction of the 99.9th percentile using the normal distribution has an error of less than 3 percentiles. Additionally, only 6 of the 350 instances predicted an LBD that was in the 100th percentile and all 6 of these instances solved in less than 130 conflicts hence the prediction was made with very little data. |
|
|
Fig. 6. Histogram of the actual percentiles of the LBD predicted to be the 99.9th99.9th percentile using a normal distribution.
|
|
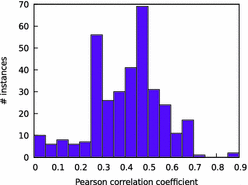
Fig. 7. Histogram of the Pearson correlation between the “previous” and “next” LBD for the instances in the SAT Competition 2017 main track benchmark. |
|
|
These figures were created by analyzing the LBD distribution at the end of a 30 min run of Glucose, and we note the results are similar before the 30 min is up. Hence the 99.9th percentile of LBDs can be approximated as the 99.9th percentile of norm(μ,σ2). The mean μμ and variance σ2 are estimated by the sample mean and sample variance of all the LBDs seen thus far, which is computed incrementally so the computational overhead is low. The 99.9th percentile of the normal distribution maps to the z-score of 3.08, that is, an LBD is estimated to be in the 99.9th percentile if it is greater than μ+3.08×σ. |
|
5.2 LBD of Next Clause |
|
|
Since at any point during the run of a solver, the LBD of the “next learnt” clause is unknown, we propose the use of machine learning to predict that LBD instead.译文:由于在求解程序运行期间的任何时刻,“next learnt”子句的LBD是未知的,我们建议使用机器学习来预测LBD。 This requires finding good features that correlate with the next LBD. 译文:这需要找到与下一个LBD相关的好特性。We hypothesize that LBDs of recent past learnt clauses correlate with the LBD of the next learnt clause.译文:我们假设最近过去学习的从句的LBD与下一个学习的从句的LBD相关。 |
|
|
In this experiment, Glucose was run on all 350 instances of the 2017 Competition main track and the LBDs of all the learnt clauses were recorded. Let n be the number of LBDs recorded for an instance. A table with two columns of length n−1 are created. For each row i in this two column table, the first column contains the LBD of the ith conflict and the second column contains the LBD of the (i+1)th conflict.
Intuitively, after the solver finishes resolving the ithith conflict, the ithith learnt clause is the “previous” learnt clause represented by the first column. Correspondingly, the “next” learnt clause is the (i+1)th(i+1)th learnt clause represented by the second column. For each instance that took more than 100 conflicts to solve, we computed the Pearson correlation between the first and second column and plot all these correlations in a histogram, see Fig. 7. 译文:对于每一个需要超过100个冲突来解决的实例,我们计算第一列和第二列之间的Pearson相关性,并将所有这些相关性绘制成柱状图,如图7所示。 |
|
|
Our results show that the “previous LBD” is correlated with the “next LBD” which supports the idea that recent LBDs are good features to predict the next LBD via machine learning.译文:我们的研究结果表明,“上一个LBD”与“下一个LBD”是相关的,这支持了最近的LBD是通过机器学习预测下一个LBD的好特征的想法。 In addition, all the correlations are positive, meaning that if the previous LBD is high (resp. low) then the next LBD is expected to be high (resp. low).译文:此外,所有的相关性都是正的,这意味着如果前期的LBD很高(resp。低)那么下一个LBD预计将是高的。低)。 Perhaps this explains why the Glucose restart policy [4] is effective. Additionally, we note that for the average instance, the LBD of the learnt clause after a restart is smaller than the LBD of the learnt clause right before that restart 74% of the time, showing the effect of restarts on LBD.译文:此外,我们注意到,在平均情况下,重新启动后的小句的LBD比重新启动前的小句的LBD小的比例为74%,说明了重新启动对LBD的影响。 |
|
| This paper proposes learning the function | |
 |
|
|
Since LBDs are streamed in as conflicts occur, an online algorithm that can incrementally adjust the θi coefficients cheaply is required. 译文:由于lbd是在冲突发生时流进来的,因此需要一种在线算法,以较低的成本增量地调整θi系数。
We use the state-of-the-art Adam algorithm [20] from machine learning literature because it scales well with the number of dimensions, is computationally efficient, and converges quickly for many problems. 译文:我们使用了机器学习文献中最先进的Adam算法[20].译文:因为它可以很好地随维数扩展,计算效率高,对许多问题收敛很快。
The Adam algorithm is in the family of stochastic gradient descent algorithms that adjusts the coefficients to minimize the squared error, where the error is the difference between the linear function’s prediction and the actual next LBD.译文:Adam算法属于随机梯度下降算法家族,调整系数以最小化平方误差,其中误差是线性函数的预测和实际下一个LBD之间的差异。 The algorithm computes the gradient of the squared error function and adjusts the coefficients in the opposite direction of the gradient to minimize the squared error function. For the parameters of Adam, we use the values recommended by the original authors [20].译文:该算法计算平方误差函数的梯度,并在梯度的相反方向调整系数,以使平方误差函数最小。对于Adam的参数,我们使用了原作者[20]推荐的值。 |
|
 |
|
| The new restart policy, called machine learning-based restart (MLR) policy, is shown in Algorithm 1. Since the mean, variance, and coefficients are computed incrementally, MLR has a very low computational overhead.译文:新的重启策略,称为基于机器学习的重启(MLR)策略,如算法1所示。由于均值、方差和系数是递增计算的,MLR的计算开销非常低. | |
6 Experimental Evaluation

|
|
|
To test how MLR performs, we conducted an experimental evaluation to see how Glucose performs with various restart policies. Two state-of-the-art restart policies are used for comparison with MLR: Glucose (named after the solver itself) [4] and Luby [22]. The benchmark consists of all instances in the application and hard combinatorial tracks from the SAT Competition 2014 to 2017 totaling 1411 unique instances. The Glucose solver with various restart policies were run over the benchmark on StarExec. For each instance, the solver was given 5000 s of CPU time and 8 GB of RAM. The results of the experiment are shown in Fig. 8. The source code of MLR and further analysis of the experimental results are available on our website [1]. |
|
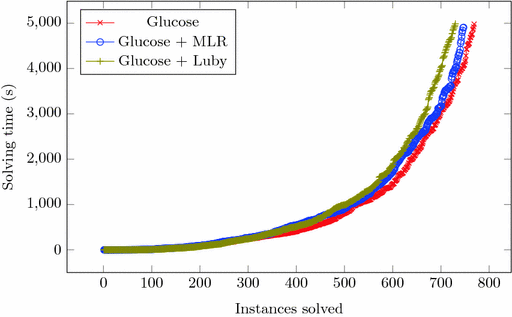
Fig. 8. Cactus plot of two state-of-the-art restart policies and MLR. A point (x, y) is interpreted as x instances have solving time less than y seconds for the given restart policy. Being further right means more instances are solved, further down means instances are solved faster. 译文:越右意味着解决的实例越多,越低意味着解决的实例越快。 |
|
|
The results show that MLR is in between the two state-of-the-art policies of Glucose restart and Luby restart. For this large benchmark, MLR solves 19 instances more than Luby and 20 instances fewer than Glucose. 译文:结果表明,MLR处于葡萄糖重启和卢比重启这两种最先进的策略之间。对于这个大型基准测试,MLR比ruby多解决了19个实例,比Glucose少解决了20个实例。 Additionally, the learned coefficients in MLR σ1,σ2,σ3σ1,σ2,σ3corresponding to the coefficients of the features representing recent past LBDS are nonnegative 91% of the time at the end of the run. This reinforces the notion that previous LBDs are positively correlated with the next LBD.译文:这强化了一个概念,即之前的LBD与下一个LBD正相关。 |
|
7 Related Work
| Restart policies come in two flavors: static and dynamic. Static restart policies predetermine when to restart before the search begins. The state-of-the-art for static is the Luby [22] restart heuristic which is theoretically proven to be an optimal universal restart policy for Las Vegas algorithms. Dynamic restart policies determine when to restart on-the-fly during the run of the solver, typically by analyzing solver statistics. The state-of-the-art for dynamic is the restart policy proposed by Glucose [4] that keeps a short-term and a long-term average of LBDs. The short-term is the average of the last 50 LBDs and the long-term is the average of all the LBDs encountered since the start of the search. If the short-term exceeds the long-term by a constant factor then a restart is triggered. Hence the Glucose policy triggers a restart when the recent LBDs are high on average whereas the restart policy proposed in this paper restarts when the predicted LBD of the next clause is high. Biere et al. [8] propose a variation of the Glucose restart where an exponential moving average is used to compute the short-term and long-term averages. Haim and Walsh [15] introduced a machine learning-based technique to select a restart policy from a portfolio after 2100 conflicts. The MABR policy [24] uses multi-armed bandits to minimize average LBD by dynamically switching between a portfolio of policies. Our use of machine learning differs from these previous methods in that machine learning is part of the restart policy itself, rather than using machine learning as a meta-heuristic to select between a fixed set of restart policies. | |
8 Conclusion
|
We showed that restarts positively impact the clause learning of CDCL solvers by decreasing the LBD of learnt clauses (thus improving their quality) compared to no restarts. However restarting too frequently is computationally expensive. We propose a new restart policy called MLR that tries to find the right balance in this trade-off. We use z-scores of the normal distribution to efficiently approximate the high percentiles of the LBD distribution. Additionally, we use machine learning to predict the LBD of the next clause, given the previous 3 LBDs and their pairwise products. Experimentally, the new restart policy is competitive with the current state-of-the-art. |
|
|
Proof-complexity theoretic Considerations: Theorists have conjectured that restarts give the solver more power in a proof-complexity sense than a solver without restarts. A CDCL solver with asserting clause learning scheme can polynomially simulate general resolution [26] with nondeterministic branching and restarts. It was independently shown that a CDCL solver with sufficiently random branching and restarts can simulate bounded-width resolution [2]. It remains an open question whether these results hold if the solvers does not restart. This question has remained stubbornly open for over two decades now. We refer the reader to the excellent articles by Buss et al. on attempts at understanding the power of restarts via proof-complexity theory [9, 10].译文:我们建议读者参考巴斯等人关于试图通过复杂性证明理论理解重启的力量的优秀文章[9,10]。 |
|
References
|
|