布尔约束传播--文献学习Unit Clause Small Clause Current Partial Assignment Clause Database Clause Sharing

Unit Clause Small Clause Current Partial Assignment Clause Database Clause Sharing 

 

对并行求解的理解：并行主要采用组合投资方式或分而治之理论策略。

（1）对已分治策略详见Non-Portfolio approaches are mostly based on the divide-and-conquer paradigm [2,13].

（2）主流的组合投资方式的核心：

• The main idea is to exploit the complementarity between different sequential CDCL strategies to let them compete on the same formula with more or less cooperation between them [10,6,16,1].译文：其主要思想是利用不同顺序CDCL策略之间的互补性，让它们或多或少地在同一公式上竞争[10,6,16,1]。
• Each thread deals with the whole formula and cooperation is achieved through the exchange of learnt clauses.译文：每一条主线都涉及到整个公式，合作是通过习得的子句的交换来实现的。

---

 

Abstract

Managing learnt clauses among a parallel, memory shared, SAT solver is a crucial but difficult task. Based on some statistical experiments made on learnt clauses, we propose a simple parallel version of Glucose that uses a lazy policy to exchange clauses between cores. This policy does not send a clause when it is learnt, but later, when it has a chance to be useful locally. We also propose a strategy for clauses importation that put them in ”probation” before a potential entry in the search, thus limiting the negative impact of high importation rates, both in terms of noise and decreasing propagation speed.

译文：该策略在学习时不发送子句，而是在以后，当它有机会在局部有用时发送子句。 译文：此外，我们亦提出一套条款输入策略，在潜在输入者进入搜索前先进行“试用”，以限制高输入率对噪音及传播速度的负面影响。

Keywords

Unit Clause 　　Small Clause 　　Current Partial Assignment 　　Clause Database 　　Clause Sharing

 

1 Introduction

	The success story of SAT solving is one of the most impressive in recent computer science history. The theoretical and practical progresses observed in the area had a direct impact in a number of connected areas. SAT solvers are nowadays used in many critical applications (BMC [5], Bio-informatics [17] . . . ) by direct encodings of problems to propositional logic (often leading to huge formulas), or by using SAT solvers on an abstraction level only。
	However, if until now measured progresses are quite impressive, the recent trends in computer architecture are forcing the community to study new efficient frameworks, by considering the native parallel (and sometimes massively parallel) architecture of current and upcoming computers.     CPU speed is stalling, but the number of cores is increasing.译文：CPU速度正在停止，但是内核的数量在增加。 Computers with one shared memory and a large number of cores are the norm today.译文：拥有一个共享内存和大量核的计算机是当今的标准。 A few specialized cards even allow more than two hundreds threads on the same board.译文：一些专用卡甚至允许在同一板上超过200个线程。 Thus, designing efficient and scalable parallel SAT solvers is now a crucial challenge for the community [11].译文：因此，设计高效和可扩展的并行SAT解决方案现在是社区的一个关键挑战。 Existing approaches can be roughly partitioned in two.译文：现有的方法可以大致分为两部分。 Firstly, the ”portfolio” approach tries to launch in parallel a set of solvers on the same formula. This can be trivially done by running the best known solvers without any communications [19] or, more interestingly, with communication between threads. This communication is generally limited to learnt clauses sharing [10,1,6].译文：首先，“投资组合”方法试图在同一公式上并行地启动一组求解器。这可以通过运行最著名的解决方案而不进行任何[19]通信，或者更有趣的是，在线程之间进行通信来简单地完成。这种交流一般仅限于学习的子句共享[10,1,6]。 Secondly, the divide and conquer approach tries first to reduce the whole formula in smaller ones and then solve them [2,13,12] with or without any communications. Note that some attempts have been made on combination of portfolio and divide and conquer approaches [7].译文：其次，分而治之法首先尝试将整个公式简化为较小的公式，然后求解[2,13,12]，无论是否进行了通信。注意，已经对组合投资组合和分而治之方法[7]进行了一些尝试。
	In our approach, we would like to consider CDCL solvers as clauses producer engines and thus, in this case, the current divide and conquer paradigm may not be ideal because the division is made on the variable search space, not on the proof space.译文：在我们的方法中，我们希望将CDCL求解器视为子句生成引擎，因此，在这种情况下，当前的分治范例可能并不理想，因为分治是在变量搜索空间上进行的，而不是在证明空间上。 When designing a clause sharing parallel CDCL solver, an important question arises: which clauses to export and import? The more is not the best. Importing too many clauses will completely paralyze the considered thread.译文：在设计共享并行CDCL解决程序的子句时，出现了一个重要问题:要导出和导入哪些子句?多多益善。导入太多子句将完全瘫痪所考虑的线程。 If we have N threads sending its clause with probability p then, after C conflicts, each thread will have on average C learnt clauses and p × (N − 1) × C imported clauses. Thus, keeping p as low as possible is critical. Too many imported clauses by too many distinct threads will destroy the effort of the current thread to focus on a subproblem. This problem is not new and was already mentioned and partially answered by one of the first parallel SAT solver: MANYSAT [10,8].译文：这个问题不是新出现的，并且已经被第一个并行的SAT解决方案之一MANYSAT提到并部分回答了。
	Let us summarize the original contributions of our approach.译文：让我们总结一下我们的方法最初的贡献。 First, we try to carefully identify clauses that have a chance to be useful locally (even locally, just a part of produced clauses are in fact really useful). These clauses will be detected ”lazily” before exporting them. 译文：首先，我们尝试仔细地识别有可能在本地有用的子句(即使是局部的，也只有一部分产生子句才是真正有用的)。   Secondly, we don’t directly import clauses. We put them in ”probation” before adding them to the clauses database, thus limiting their impact on the current search.译文：我们不直接进口条款。在将它们添加到子句数据库之前，我们先对它们进行“试用”，从而限制它们对当前搜索的影响。 In the following section, we review the different approaches proposed for parallelizing Modern SAT solvers. Then, in section 3, we detail the principal ”Lazy” clause exchange policy proposed in GLUCOSE-SYRUP, our parallel version of GLUCOSE. Then, we propose some experiments (section 5) and conclude.

 2 Preliminaries and Previous Works

*	We assume the reader familiar with the essentials of propositional logic, SAT solving and CDCL solvers. 译文：我们假定读者熟悉命题逻辑、SAT求解和CDCL求解器的基本内容。   These solvers are branching on literals and, at any step of the search, ensure that all the unit clauses w.r.t the current partial assignment are correctly ”propagated” until an empty clause is found (a backtrack is then fired, or the unsatisfiability is proven) or a total assignment is reached (the formula is SAT). Each time a conflict occurs, a clause (called asserting clause) is learnt and is used to force backtracking, leading to new propagations. 译文：这些求解器都是基于文字的分支，并且在搜索的任何步骤中，确保所有的unit子句都是w.r。t当前的部分赋值被正确地“传播”，直到找到一个空子句(然后触发回溯，或者证明了不可满足性)，或者达到了全部赋值(公式为SAT)。每次发生冲突时，都会学习一个子句(称为断言子句)，并用于强制回溯，从而导致新的传播。 Of course, many additional ingredients are essential but reviewing all of them will clearly be beyond the scope of this paper。译文：当然，许多额外的成分是必要的，但回顾所有这些显然超出了本文的范围
	The important point to be emphasized here, even for the non specialist, is that solvers are learning a lot of clauses (more than 5000 per second), partially guided in its search by previous learnt clauses forcing new unit propagations. 译文：这里需要强调的是，即使对于非专业人士，求解器也需要学习大量的子句(超过5000个/秒)，部分是在之前学习的子句的引导下进行搜索，迫使新的单位传播。   以下讲解学习子句质量评价和子句集的管理   The management of the clauses database was firstly pointed out as an essential ingredient with the design of GLUCOSE [4].译文：GLUCOSE[4]的设计中，首先指出子句数据库的管理是必不可少的组成部分。 Indeed, keeping too many learnt clauses will slow down the unit propagation process, while deleting too many of them will break the overall learning benefit. Consequently, identifying good learnt clauses – relevant to the (future) proof derivation – is clearly an important challenge. 译文：的确，保留过多的已学习子句会减慢单元传播的进程，而删除过多的子句会破坏整体的学习效益。因此，识别与(将来的)证明推导相关的好习得子句显然是一个重要的挑战。   The first proposed quality measure followed the success of the activity-based “VSIDS” heuristic [18]. More precisely, a learnt clause is considered relevant (in the future) to the proof, if it is involved more often in recent conflicts, i.e. used to derive asserting clauses by resolution. This deletion strategy supposes that a useful clause in the past would be useful in the future. In [4], the authors proposed a more accurate measure called LBD (Literal Block Distance) to estimate the quality of a learnt clause. 三种子句质量评价方法 译文：这种删除策略假设过去有用的子句将来也会有用——子句activity（based“VSIDS”）和在近期经常使用； 译文：在[4]中，作者提出了一种更精确的测量方法，称为LBD(文字块距离)，用来估计一个已习得子句的质量。  This measure is based on the number of distinct decision levels occurring in a learnt clause and computed when the clause is learnt. Intensive experiments  demonstrated that clauses with small LBD values are used more often than those of higher LBD ones.译文：密集的实验表明，小LBD值的子句比高LBD值的子句使用得更多。 This measure is important here because it seems to offer a good prediction for the quality of a clause, and it seems to be a good starting point if we may want to build a good clause exchange policy between threads. 译文：这个度量在这里很重要，因为它似乎可以很好地预测子句的质量，而且如果我们想在线程之间构建一个好的子句交换策略，它似乎是一个很好的起点。 However, as we will see, the LBD measure seems essentially relevant to the current search only. Even if it has been proven to be more relevant than size (see below the PLINGELING strategy), a small LBD clause may not be of great interest for another thread.译文：即使已经证明它比大小更相关(参见下面的PLINGELING策略)，一个小的LBD子句可能对另一个线程不是很感兴趣。
	2.1 About Clause-Sharing Parallel Approaches
	A number of previous works have been proposed around Portfolio approaches, with more or less cooperation/diversification between threads.译文：许多以前的作品都是围绕投资组合方法提出的，线程之间或多或少的合作/多样化。 The main idea is to exploit the complementarity between different sequential CDCL strategies to let them compete on the same formula with more or less cooperation between them [10,6,16,1].译文：其主要思想是利用不同顺序CDCL策略之间的互补性，让它们或多或少地在同一公式上竞争[10,6,16,1]。 Each thread deals with the whole formula and cooperation is achieved through the exchange of learnt clauses.译文：每一条主线都涉及到整个公式，合作是通过习得的子句的交换来实现的。 Non-Portfolio approaches are mostly based on the divide-and-conquer paradigm [2,13]. We here focus on Portfolio parallel approaches in this section. 译文：非投资组合方法大多基于分治范式[2,13]。在本节中，我们主要关注投资组合并行方法。
	As mentioned in the introduction, the size of the learnt clause database is crucial for sequential solvers. This is not only true for maintaining a good unit propagation speed, but this seems also essential to guide the solver to the best possible proof it can build. 译文：正如引言中提到的，learn子句数据库的大小对于顺序求解器至关重要。这不仅对于保持良好的单位传播速度是正确的，而且对于引导求解器找到它所能构建的最好的证明似乎也是必要的。   These observations are even more crucial when many threads are cooperating. For a parallel portfolio SAT solver, it is not desirable to share as many clauses as possible and, obviously, each of the clause-sharing portfolio approaches mentioned above had to develop its own strategy to carefully select the clauses to share. 译文：当多个线程协同工作时，这些观察结果甚至更加重要。对于一个并行的投资组合SAT求解器，它是不可取的分享尽可能多的条款，显然，上面提到的每一个子句共享投资组合方法必须发展自己的策略来仔细选择要分享的子句。 A first and quite natural solution to limit the number of exported clauses is to simply share the smallest clauses according to their size. This was the strategy adopted in [10]. Based on the observation that small clauses appear less and less during the search, authors of MANYSAT proposed a very nice dynamic clause sharing policy using pairwise size limits to control the exchange between threads [9]. 译文：限制导出子句数量的第一个和非常自然的解决方案是根据它们的大小共享最小的子句。这就是[10]所采用的策略。基于小子句在搜索过程中越来越少的现象，MANYSAT的作者提出了一个非常好的动态子句共享策略，使用成对的大小限制来控制线程[9]之间的交换。 In the same paper, they also anecdotally proposed another dynamic policy based on the activity of variables according to the VSIDS heuristic. However, such weighting function is highly fickle and, unfortunately, the top-ranked variable (according to VSIDS) may not be of any interest only 0.1s later (according to the same VSIDS). 译文：在同一篇论文中，他们还根据VSIDS启发式，轶事地提出了另一种基于变量活动的动态策略。但是，这样的权重函数变化无常，而且不幸的是，只有在0.1秒之后(根据VSIDS)，排名最高的变量才可能没有任何意义。 It is thus hopeless to try to directly rely on this highly dynamic strategy to measure the quality of imported clauses. In Penelope [1], authors use the freezing strategy to manage learnt clauses [3] allowing to share much more clauses without a high overhead. Finally, PLINGELING shares all clauses with a size less than 40 and LBD less than 8 [6]. 译文：因此，试图直接依靠这种高度动态的策略来衡量进口条款的质量是无望的。 译文：在Penelope[1]中，作者使用冻结策略来管理学到的[3]条款，从而在不增加开销的情况下共享更多的条款。最后，PLINGELING共享size小于40和LBD小于8[6]的所有子句。
	2.2 Portfolio or Not Portfolio
	We chose to focus, in this paper, on a Clause-Sharing Parallel Approach of GLUCOSE engines. This approach is often misleadingly called “Portfolio” because, in general, each engine must have its own configuration to ensure orthogonal searches between threads. However, considering that GLUCOSE is seen as an efficient proof producer, this idea of “orthogonal” search on variables assignments is not clear. We would like to keep the word “portfolio” only to approaches that tries to take advantage of running many distinct solvers, each of them specialized on a subset of problems, and thus focusing on the competition between each configuration strengths. In our approach, we will restrict the “orthogonal” search to its minimum. Thus, we rather see our approach as a simple parallelization effort of the same engine rather than a “portfolio” one. Our final goal is to see all solvers working together to produce a single proof, as short as possible.

 3 Lazy Clause Exchange

	This section describes the strategy we propose for parallelizing GLUCOSE. This strategy is only based on how to identify “good” clauses to export and to import. The parallel solver is called “GLUCOSE-SYRUP” (i.e. a lot of glucose).译文：该策略仅基于如何识别要导出和导入的“好”子句。
	3.1 Identifying Useless Clauses?
	The identification of useless clauses is still an open question for sequential solvers. We thus do not pretend to fully answer it in this section. However, let us take some time in this section to report a set of experiments on sequential solvers that motivated the strategies proposed in GLUCOSE-SYRUP.
	Viewing CDCL solvers as clauses producers is not the mainstream approach. However, as it was reported in [15], this may be one of the key points for an efficient parallelization. This work suggested the following very simple experiment. When an instance is UNSAT (proven by GLUCOSE), we identify clauses that occur in the proof, and measure how many of them are useless for the proof. The term “useless” is now clearly defined: it does not occur in the final proof for UNSAT. However, it should be noticed here that this definition can be misleading. A “useless“ clause may be crucial at some stage of the search to update the heuristic or to propagate a literal earlier in the search tree. Thus, this notion should be used with caution.
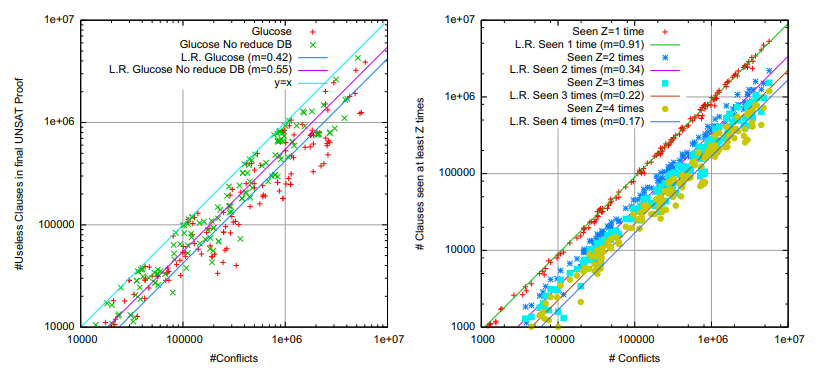
	Fig. 1. (Left) Useless clauses in the final UNSAT proof w.r.t the total number of generated clauses. Glucose no reduce DB is a hacked version of GLUCOSE that do not perform any learnt clause removal. Experiments are done on a set of 250 UNSAT problems from competitions 2011 and 2013. Only successful run are collected. “L.R.” stands for “Linear Regression” with y = m × x + n. (Right) Scatter plot of the number of conflicts (X axis) against the number of clauses seen at least Z={1, 2, 3, 4} times for all the successful launches (on SAT 2011, satelited, problems).
	This being said, Figure 1-Left shows a surprisingly large number of useless clauses. On the original GLUCOSE solver, 45% of the learnt clauses are, on average, not useful. This result is not the only surprise here. When GLUCOSE keeps all its clauses (called “Glucose No Reduce DB” on the figure), this number is even more important (55%!). This mean that keeping all the clauses, even if the final number of conflicts is smaller than the original GLUCOSE, leads to a larger proportion of useless clauses. We could have expected the opposite to happen: the aggressive clause database reduction in GLUCOSE throws away many clauses. Those clauses will not have a chance to occur in the proof afterwards. As a very short conclusion on this figure, we see that even for a single engine, considering the usefulness of a clause is not an easy task. Moreover, around half of the generated clauses are not useful. Sending them to other threads may not be the right move to do.
	3.2 Lazy Exportation of Interesting Clauses
	Before presenting the export strategy in GLUCOSE-SYRUP, let us focus now on Figure 1-Right. This figure shows how many clauses are seen at least Z={1,2,3,4} times during all conflicts analysis of GLUCOSE (not propagations). The figure already shows that 91% of the clauses, on all the problems, are seen at least once. However, when Z=2, this ratio drops to 34%, then 22% and 17% for Z=4. This suggests to export only clauses seen at least Z times, and to fix Z>1. We propose to simply fix Z=2 to already get rid of 66% (100-34%) of the locally generated clauses, and to send only clauses seen two times. The strategy is called “lazy” because we do not try to guess in advance the usefulness of a clause. Instead, we simply (and somehow “lazily”) wait for the clause to be seen twice in the conflict analysis.
	To refine the above observations, we conducted two more experiments. Firstly, we supposed that, in many cases, a learnt clause had a high probability to be seen in the very next conflict analysis, because the clause is immediately propagated and is clearly at one of the deepest levels of the search tree. However, as clearly shown Figure 2-Left, only 41% of the learnt clauses are immediately used for conflict analysis (remember that 91% of the clauses are seen at least once). This means that we really need a lazy strategy to identify interesting clauses: we cannot suppose any locality (in the number of conflicts) for identifying when a clause will be used for the second time.
	As we already pointed out in the second section, PLINGELING is using a fixed strategy to filter the exported clauses. It restricts the exportations to clauses of LBD smaller than 8 and size smaller than 40. We use a more flexible limit in our approach. We automatically adapt the LBD and size thresholds according to the characteristics of the current clauses in the learnt clause database. Each time a clause database reduction is fired, the current median LBD value and the average size of learnt clauses are updated. In most of the cases, we observed that the dynamic values are more relaxed than the fixed values of PLINGELING.
	Of course, unit clauses and binary clauses are exported without any restriction, as soon as they are learnt. We extended this strategy to all glue clauses (clauses of LBD=2). Thus the above strategy is for clauses of at least size 3 that are not glues.
	3.3 Lazy Importation of Clauses
	We have seen how carefully choosing which clauses to send can be crucial for limiting the communication overhead. The extra work for importing clauses can also be limited if we can consider the following four points. (1) Importing clauses after each conflict may have an important impact (and a negative one) on all solvers strategies (need to check the trail, and to backjump when necessary, breaking the solver locality, . . . ) ; (2) Importing clauses may have an important impact on the cleaning strategies of GLUCOSE (the learnt clause database will increase much more faster) ; (3) The more is not the best. A ”bad” clause may force the solver to propagate a literal in the wrong direction, i.e. it will not be able to properly explore the current subproblem ; (4) There is no simple way of computing the LBD of an incoming clause. This measure cannot be used because LBD is relative to the current search of each solver, and a good clause for one thread may not be good for another one. So, before adding a clause to the solver database, one has to carefully ensure that the clause is useful for the current search.
	For the first point (1), we decided to import clauses (unary, binary and others) only when the solver is at decision level 0, i.e. right after a restart or right after it learnt a unit clause. This event occurs a lot during the search (many times per second) and this rate is clearly sufficient for a good collaboration. For the second point, (2) we import clauses in another set of clauses, that can have its own cleaning rules and will not pollute GLUCOSE cleaning strategies on its learnt clauses.
	The main ”Lazy” solution we propose is a solution for the two last items, (3) and (4). It is somehow related to the PSM strategy [3]: when a clause is imported, we watch it only by one literal. This watching scheme does not guarantee anymore that all unit propagations are performed after each decision. However, this is sufficient to ensure that any conflicting clause will be detected during unit propagation. The interest of this technique is twofold. Firstly, the clause will not pollute the current search of the solver, except when it is falsified. Secondly, the cost for handling the set of imported clause is heavily reduced. This technique can be viewed as a more reactive PSM strategy.
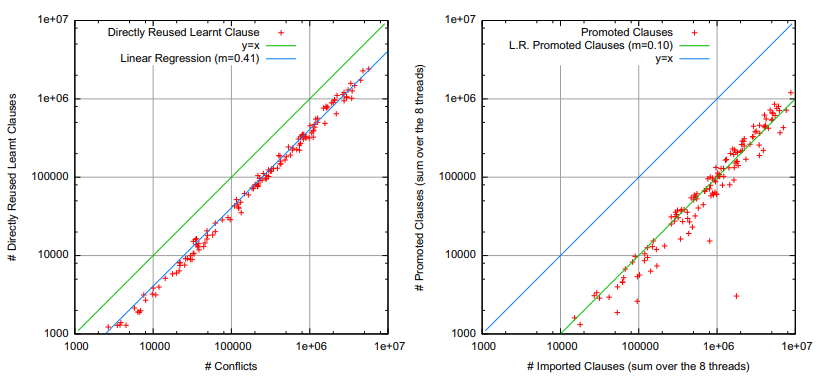
	Fig. 2. Left Scatter plot of the number of conflicts (X axis) against the number of clauses directly reused in the next conflict analysis (on a single engine GLUCOSE). Right Scatter plot of the number of imported clauses (1-Watched clauses) against promoted clauses (clauses found empty, and pushed to the 2-Watched literal scheme) on successful run of GLUCOSE-SYRUP with 8 threads on the SAT’11 competition benchmarks (after SatElite).
	Figure 2-Right shows that only 10% of the imported clauses are falsified at some point. It demonstrates how well founded is our strategy for the importation: 90% of the clauses are never falsified by the solver strategy. Technically speaking, as soon as an imported clause is falsified, it is “promoted”, i.e. we watch it with 2 literals like an internal learnt clause. The clause is then part of the solver search strategy, and can be used for propagation.

4 Experiments

	In this section, we compare PLINGELING [6], the winner of the SAT’13 competition with our first version of GLUCOSE-SYRUP. Let us notice here that this version is still preliminary in the sense that absolutely no tuning has been conducted on the set of parameters we chose for the 8 threads. 译文：这里我们要注意的是，从这个意义上说，这个版本还处于初级阶段，我们完全没有对我们为8个线程选择的一组参数进行调优。     All threads are identical except their parameter playing on the VSIDS scoring scheme. One thread is however configured like GLUCOSE 2.0 version.  译文：除了在VSIDS评分方案中运行的参数外，所有线程都是相同的。不过，有一个线程的配置类似于葡萄糖2.0版本。
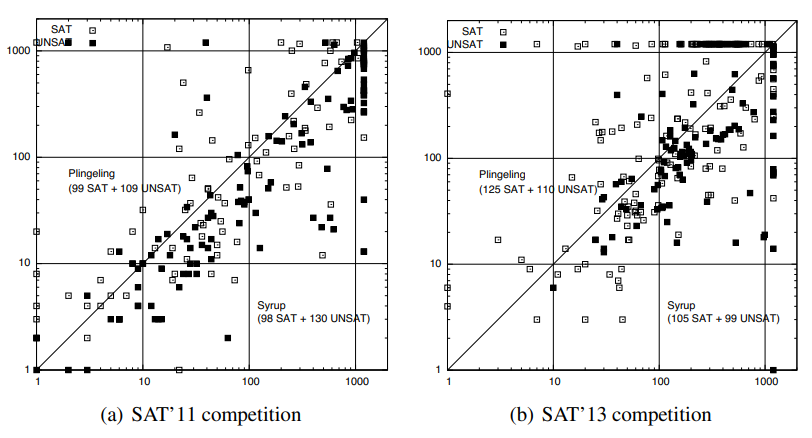
	Fig. 3. GLUCOSE-SYRUP VS PLINGELING on SAT competitions benchmarks, application track. Each dot represents an instance. A dot below the diagonal indicates an instance solved faster with GLUCOSE-SYRUP. On SAT’11 Problems (a): PLINGELING: 208 / GLUCOSE-SYRUP: 228. On SAT’13 Problems(b): PLINGELING: 235 / GLUCOSE-SYRUP: 204.
	Figure 3 compares PLINGELING [6], the winner of the SAT’13 competition against GLUCOSE-SYRUP using the classical scatter plots. We use two test sets of problems, because each solver has its own strengths and weaknesses. Let us start with the SAT’11 competition, application track, problems. For this test set, GLUCOSE-SYRUP is able to solve 228 instances (98 SAT and 130 UNSAT) whereas PLINGELING is able to solve 208 instances (99 SAT and 109 UNSAT). Note that the sequential version of GLUCOSE only solves 187 instances (87 SAT and 100 UNSAT). GLUCOSE-SYRUP clearly extends the efficiency of GLUCOSE on UNSAT problems to the parallel case. Moreover, many points are below the diagonal indicating that, in many cases, our solver is faster (even for SAT instances) than PLINGELING. This result may be partially explained by all the inprocessing [14] techniques embedded in PLINGELING, that may not be efficient enough with the time we fixed. More importantly, we think the big gap observed for UNSAT instances can come from the ability of GLUCOSE-SYRUP to share and exploit promising clauses. It is also fair to notice that GLUCOSE, the underlying sequential engine is quite good in solving those UNSAT instances. Let us continue with instances coming from SAT’13 competition. Here, the picture is totally inverted. Results are clearly in favor of PLINGELING. It solves 235 instances (125 SAT and 110 UNSAT) whereas GLUCOSE-SYRUP is only able (GLUCOSE the underlying solver can only solve 173 instances (93 SAT and 80 UNSAT)) to solve 204 (105 SAT and 99 UNSAT). This is a big difference. However, if we study this result more deeply, we can observe that, here again, in many cases GLUCOSE-SYRUP is faster than PLINGELING. The differences between the two approaches arise after 500 seconds: PLINGELING is able to solve difficult and/or particular problems, by exploiting inprocessing techniques (xor-reasoning, equivalence checking, . . . ). The SAT’13 competition is indeed the first competition to contain so many problems with xor chains and counters. On this set of problem, inprocessingstechniques are mandatory. However, for genuine parallel CDCL solvers, we showed that GLUCOSE-SYRUP is clearly a new parallel approach offering very good performances.

5 Conclusion

Clauses sharing among threads in a parallel SAT solver remains a difficult task. By experimentally studying learnt clauses usefulness, we propose a lazy policy for clauses exports. Furthermore, we propose a new scheme for clauses importations by putting them in probation before adding them to the clauses database. Experiments based on our solver GLUCOSE shows that this method for parallelization allows a very good scaling up of the underlying sequential engines.

译文：在并行SAT求解器中线程间共享子句仍然是一项困难的任务。 译文：通过对已学习的子句有效性的实验研究，我们提出了一种用于子句输出的懒散策略。 译文：此外，我们提出了一种新的子句导入方案，即先对子句进行试用，然后再添加到子句数据库中。 译文：基于求解器葡萄糖的实验表明，这种并行化方法可以很好地扩展底层顺序引擎。

 

 

References

1. 1.
   Audemard, G., Hoessen, B., Jabbour, S., Lagniez, J.-M., Piette, C.: Revisiting clause exchange in parallel SAT solving. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 200–213. Springer, Heidelberg (2012)CrossRefGoogle Scholar
2. 2.
   Audemard, G., Hoessen, B., Jabbour, S., Piette, C.: An effective distributed D&C approach for the satisfiability problem. In: 22nd Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP 2014) (February 2014)Google Scholar
3. 3.
   Audemard, G., Lagniez, J.-M., Mazure, B., Saïs, L.: On freezing and reactivating learnt clauses. In: Sakallah, K.A., Simon, L. (eds.) SAT 2011. LNCS, vol. 6695, pp. 188–200. Springer, Heidelberg (2011)CrossRefGoogle Scholar
4. 4.
   Audemard, G., Simon, L.: Predicting learnt clauses quality in modern SAT solvers. In: Proceedings of IJCAI, pp. 399–404 (2009)Google Scholar
5. 5.
   Biere, A., Cimatti, A., Clarke, E., Zhu, Y.: Symbolic Model Checking without BDDs. In: Cleaveland, W.R. (ed.) TACAS 1999. LNCS, vol. 1579, pp. 193–207. Springer, Heidelberg (1999)CrossRefGoogle Scholar
6. 6.
   Biere, A.: Lingeling, plingeling and treengeling entering the sat competition 2013. In: Proceedings of SAT Competition 2013; Solver and Benchmark Descriptions, p. 51 (2013), http://fmv.jku.at/lingeling
7. 7.
   Gebser, M., Kaufmann, B., Schaub, T.: Multi-threaded asp solving with clasp. TPLP 12(4-5), 525–545 (2012)zbMATHMathSciNetGoogle Scholar
8. 8.
   Guo, L., Hamadi, Y., Jabbour, S., Sais, L.: Diversification and intensification in parallel SAT solving. In: Cohen, D. (ed.) CP 2010. LNCS, vol. 6308, pp. 252–265. Springer, Heidelberg (2010)CrossRefGoogle Scholar
9. 9.
   Hamadi, Y., Jabbour, S., Sais, L.: Control-based clause sharing in parallel SAT solving. In: Proceedings of IJCAI, pp. 499–504 (2009)Google Scholar
10. 10.
    Hamadi, Y., Jabbour, S., Saïs, L.: Manysat: A parallel SAT solver. Journal on Satisfiability, Boolean Modeling and Computation 6, 245–262 (2009)zbMATHGoogle Scholar
11. 11.
    Hamadi, Y., Wintersteiger, C.M.: Seven challenges in parallel SAT solving. AI Magazine 34(2), 99–106 (2013)Google Scholar
12. 12.
    Heule, M.J.H., Kullmann, O., Wieringa, S., Biere, A.: Cube and conquer: Guiding CDCL SAT solvers by lookaheads. In: Eder, K., Lourenço, J., Shehory, O. (eds.) HVC 2011. LNCS, vol. 7261, pp. 50–65. Springer, Heidelberg (2012)CrossRefGoogle Scholar
13. 13.
    Hyvärinen, A.E.J., Junttila, T., Niemelä, I.: Partitioning SAT instances for distributed solving. In: Fermüller, C.G., Voronkov, A. (eds.) LPAR-17. LNCS, vol. 6397, pp. 372–386. Springer, Heidelberg (2010)CrossRefGoogle Scholar
14. 14.
    Järvisalo, M., Heule, M.J.H., Biere, A.: Inprocessing rules. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 355–370. Springer, Heidelberg (2012)CrossRefGoogle Scholar
15. 15.
    Katsirelos, G., Sabharwal, A., Samulowitz, H., Simon, L.: Resolution and parallelizability: Barriers to the efficient parallelization of SAT solvers. In: AAAI 2013 (2013)Google Scholar
16. 16.
    Kottler, S., Kaufmann, M.: SArTagnan - A parallel portfolio SAT solver with lockless physical clause sharing. In: Pragmatics of SAT (2011)Google Scholar
17. 17.
    Lynce, I., Marques-Silva, J.: SAT in bioinformatics: Making the case with haplotype inference. In: Biere, A., Gomes, C.P. (eds.) SAT 2006. LNCS, vol. 4121, pp. 136–141. Springer, Heidelberg (2006)CrossRefGoogle Scholar
18. 18.
    Moskewicz, M., Madigan, C., Zhao, Y., Zhang, L., Malik, S.: Chaff: Engineering an efficient SAT solver. In: Proceedings of DAC, pp. 530–535 (2001)Google Scholar
19. 19.
    Roussel, O.: ppfolio, http://www.cril.univ-artois.fr/~roussel/ppfolio