文献阅读Centrality-Based Improvements to CDCL Heuristics

Centrality-Based Improvements to CDCL Heuristics

Abstract

There are many reasons to think that SAT solvers should be able to exploit formula structure, but no standard techniques in modern CDCL solvers make explicit use of structure. We describe modifications to modern decision and clause-deletion heuristics that exploit formula structure by using variable centrality. We show that these improve the performance of Maple LCM Dist, the winning solver from Main Track of the 2017 SAT Solver competition. In particular, using centrality in clause deletion results in solving 9 more formulas from the 2017 Main Track. We also look at a number of measures of solver performance and learned clause quality, to see how the changes affect solver execution.

译文：有很多理由认为SAT求解器应该能够利用公式结构，但是现代CDCL求解器中没有标准技术明确地使用结构。我们描述了利用变量中心性开发公式结构对变元分支决定策略和子句删除策略的调整。 译文：我们也查看求解器性能和学习的子句质量的一些度量，以了解这些变化如何影响求解器的执行。

 

1 Introduction

	Structure seems important in SAT research. Notions of instance structure are invoked in explaining solver performance, for example on large industrial formulas; many empirical papers relate aspects of solver performance to formula structure; and structure is key in theoretical results on both hardness and tractability.
	Despite this, no standard method used in modern CDCL SAT solvers makes direct use of formula structure. (We exclude local structure such as used in resolving two clauses or assigning a unit literal.) The heuristics in CDCL solvers focus on local properties of the computation — what the algorithm has recently done — ignoring overall structure. The VSIDS and LRB decision heuristics give strong preference to variables that have been used many times recently, while clause deletion based on LBD and clause activity selects clauses based on recent use and an indicator of likelihood of being used again soon.译文：VSIDS和LRB决策启发式对最近多次使用的变量给予了强烈的偏好，而基于LBD和子句活动的子句删除则根据最近的使用和很快再次使用的可能性指标来选择子句。
	We present modifications to state-of-the-art decision and clause deletion heuristics that take structure into account by using variable betweenness centrality.译文：我们对最先进的决策和子句删除启发式算法进行了修改，通过使用变量介数中心性来考虑结构。   This measure reflects the number of shortest paths through a variable in the primal graph of the formula.译文：这个度量反映了公式的原始图中通过一个变量的最短路径的数量。 For decision heuristics, we give three different centrality-based modifications that alter VSIDS or LRB variable activities. For the clause deletion heuristic, we replace activity-based deletion with deletion based on clause centrality, a clause quality measure we believe is new.
	We demonstrate the effectiveness of the methods by implementing them in Maple LCM Dist, the winning solver from Main Track of the 2017 SAT Solver competition, and running them on the formulas from that track with a 5000 s time-out.译文：我们通过在2017年SAT求解器大赛主跑道的获胜者Maple LCM Dist中实现这些方法的有效性，并在该跑道的公式上运行这些方法，并设置了5000秒的暂停时间。 All the modifications increased the number of instances solved and reduced the PAR-2 scores. While our methods are simple, to our knowledge this is the first time that explicit structural information has been successfully used to improve the current state-of-the-art CDCL solver on the main current benchmark. We also report a number of other measures of solver performance and learned clause quality, and make some observations about these.
	Related Work.  Several papers have studied the structure of industrial CNF formulas, e.g., [6, 13, 29]. “Community structure” (CS) has been shown in industrial formulas [11] and CS quality is correlated with solver run time [2, 3, 24, 25]. CS was used in [4] to generate useful learned clauses. In [20, 23] CS was used to obtain small witnesses of unsatisfiability. [17] showed that VSIDS tends to choose bridge variables (community connectors), and [14] showed that preferential bumping of bridge variables increased this preference and improved performance of the Glucose SAT solver. [27] described a method that applies large bump values to variables in particular communities. Eigenvalue centrality of variables was studied in [15], and it was shown that CDCL decisions are likely to be central variables. Betweenness centrality was studied in [14], where it was shown that a large fraction of decision variables have high betweenness centrality, and that the performance of Glucose can be improved by preferential bumping of variables with high betweenness centrality. Some features used in learning performance prediction models, as used in SATzilla [30], are structural measures. Lower bounds for CDCL run times on unsatisfiable formulas are implied by resolution lower bounds, and formula structure is central to these [8]. Formulas with bounded treewidth are fixed parameter tractable [1], and also can be efficiently refuted by CDCL with suitable heuristics [5].

 

2 Centrality Computation

	Exactly computing betweenness centrality involves an all-pairs-shortest-paths computation, and is too expensive for large formulas. 译文：精确计算介数中心性涉及到全对最短路径的计算，对于大的公式来说代价太大。 We computed approximate centrality values using the NetworkX [22] betweenness_centrality function, with sample size parameter n / 50, where n is the number of variables. The parameter sets the number of vertices used to compute the approximation.译文：该参数设置用于计算近似值的顶点数。
	For some industrial formulas even this approximation takes too long to be useful (under SAT competition conditions), but for many formulas the approximation is fast. With a 300 s time-out, we found approximations for 217 of the 350 formulas from the main track of the 2017 competition. Figure 1 is a histogram of the centrality approximation times for these formulas, showing that a large fraction required less than 70 s.

 

	Decision Heuristics.  The VSIDS decision heuristic [21], in several variations, has been dominant in CDCL solvers for well over a decade. Recently, the LRB (Learning-Rate-Based) heuristic [16] was shown to be effective, and winners of recent competitions use a combination of VSIDS and LRB. Both employ variable “activity” values, which are updated frequently to reflect the recent variable usage.译文：两者都使用可变的“活动”值，这些值经常更新以反映最近的变量使用情况。 The update involves increasing (or “bumping”) the activity value for a variable each time it is assigned or appears during the derivation of a new learned clause.译文：更新包括每次分配变量或在派生新的学习子句期间出现变量时增加(或“改变”)该变量的活动值。 A secondary update in MapleSAT [16] and its descendants involves, at each conflict, reducing the LRB activity score of each variable that has not been assigned a value since the last restart. Maple LCM Dist uses both VSIDS and LRB, at different times during a run, and LRB activity reduction.
	In [14] we reported that increasing the VSIDS bump value for high-centrality variables during an initial period of a run improved the performance of the solver Glucose. This did not help much in solvers using LRB, but motivated further study. As in [14] we define “high-centrality” variables to be the 1/3 fraction of variables with highest centrality values. The modifications reported here are: 译文：在[14]中，我们报道在运行初期增加高中心性变量的VSIDSp碰撞值以改善求解器Glucose的性能。
	HCbump-V: We scale the VSIDS additive bump values for high-centrality variables by a factor greater than 1. In the experiments reported here, the factor is 1.15.
	HCbump-L: We periodically scale the LRB activity values of high-centrality variables by a factor greater than 1. In the experiments reported here, we scaled by a factor of 1.2 every 20,000 conflicts.
	HCnoReduce: We disable the reduction of LRB scores for “unused variables” that are also high-centrality variables.
	Clause Deletion.  The Maple LCM Dist clause deletion (or reduction) scheme was inherited from COMiniSatPS, and is as follows [7, 19]. The learned clauses are partitioned into three sets called CORE, TIER2 and LOCAL. Two LBD threshold values, t1,t2t1,t2, are used. Learned clauses with LBD less than t1t1 are put in CORE. t1t1 is initially 3 but changed to 5 if CORE has fewer than 100 clauses after 100,000 conflicts. Clauses with LBD between t1 and t2=6 are put in TIER2. Clauses with LBD more than 6 are put in LOCAL. Clauses in TIER2 that are not used for a long time are moved to LOCAL. Clause deletion is done as follows. Order the clauses in LOCAL by non-decreasing activity. If m is the number of clauses in LOCAL, delete the first m / 2 clauses that are not reasons for the current assignment. We report on the following modification:
	HCdel: Replace ordering of clauses in LOCAL by clause activity with ordering by clause centrality. We define the centrality of a clause to be the mean centrality of the variables occurring in it.

4 Performance Evaluation

	We implemented each of our centrality-based heuristics in Maple LCM Dist [19], the solver that took first place in the Main Track of the 2017 SAT Solver Competition [26]. We compared the performance of the modified versions against the default version of Maple LCM Dist by running them on the 350 formulas from the Main Track of the 2017 solver competition, using a 5000 s time-out. Computations were performed on the Cedar compute cluster [9] operated by Compute Canada [10]. The cluster consists of 32-core, 128 GB nodes with Intel “Broadwell” CPUs running at 2.1GHz.
	We allocated 70 s to approximate the variable centralities, based on the cost-benefit trade-off seen in Fig. 1: Additional time to obtain centralities for more formulas grows quickly after this point. If the computation completed, we used the resulting approximation in our modified solver. Otherwise we terminated the computation and ran default Maple LCM Dist. The choice of 70 s is not crucial: Any cut-off between 45 and 300 s gives essentially the same outcome. Centrality values were obtained for 198 of the 350 formulas. Our 5000 s timeout includes the time spent on centrality computation, whether or not the computation succeeded.
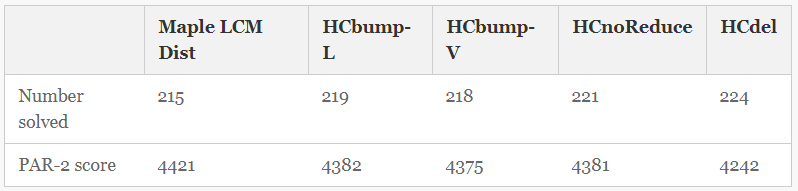
	Table 1. Number of formulas solved (out of 350) and PAR-2 score, for default Maple LCM Dist and our four modified versions. Table 1 gives the number of instances solved and the PAR-2 score for each method. All four centrality-based modifications improved the performance of Maple LCM Dist by both measures.
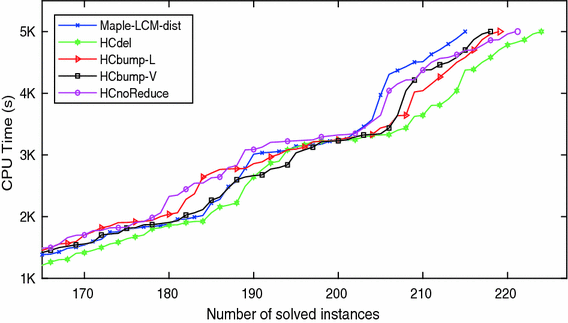
	Fig. 2. Cactus plot comparing performance of default Maple LCM Dist and our four modified versions.
	Figure 2 gives the “cactus plot” (inverse cumulative distribution function) for the runs. All four modifications result in improved performance. HCdel, which uses centrality-based clause deletion, is the best, and also out-performs default Maple LCM Dist for almost all smaller cut-off time values. The other methods, which modify the decision heuristic, improve on the default for all times longer than 3300 s. The two methods that modify LRB under-perform the default on easy formulas, but catch up at around 3200 s.
	Families Affected. It is natural to wonder if these improvements are due to only one or two formula families. They are not. Table 2 shows, for each of our four modified solvers, how many formulas it solved that default Maple LCM Dist did not, and how many families they came from.
	Table 2. Number of families involved in formulas solved by our modified solvers by not by default Maple LCM Dist.

5 Performance Details

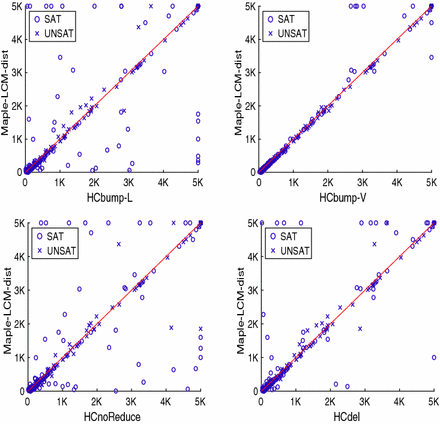
	Reliability.  There is an element of happenstance when using a cut-off time. For example, the “best” method would be different with a cut-off of 2800 s, and the “worst” would be different with a cut-off of 2200 s. Run-time scatter plots give us an alternate view. Figure 3 gives scatter plots comparing the individual formula run-times for each of our four modified solvers with the default Maple LCM Dist. We observe:
	Fig. 3. Comparison of run-times of default Maple LCM Dist with each of our modified versions. Each plot shows all instances that were solved by at least one of the two solvers represented. Satisfiable formulas are denoted with ∘∘, unsatisfiable formulas with x.
	In each plot many points are lined up just below the main diagonal. These are the formulas without centralities, for which we pay a 70-s penalty. The most reliable method is HCdel. It solved the most, was faster on 70% of formulas with centralities and had significant slow-down for only 4 formulas. HCbump-V caused the least variation: it solved more formulas, but gave significant speedups on only a few others. The two LRB modifications, HCbump-L and HCnoReduce, were very “noisy”, speeding up many formulas but also slowing down quite a few. It is very interesting that very large differences in run-time were mostly for satisfiable formulas.
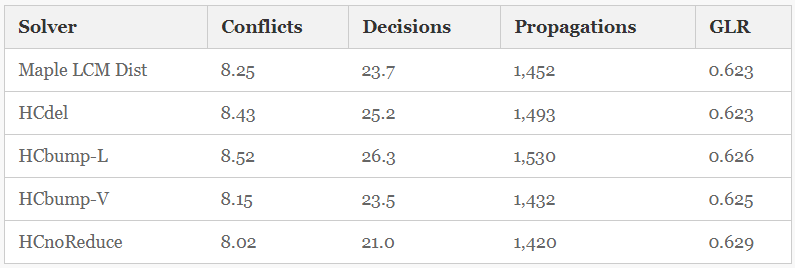
	Reasoning Rates.  Here, we look at measures of the rate of solver reasoning or search (as distinct from, for example, quality of reasoning or total time). Table 3 shows, for each method, the mean decision rate, the mean conflict production rate, the mean unit propagation rate, and the mean Global Learning Rate (GLR). GLR, defined as the ratio of the number of conflicts to the number of decisions, was introduced in [18], where it was observed that decision heuristics producing a higher GLR had reduced solving times. We observe:
	Consistent with the observations in [18], decision heuristic changes that improved performance increased GLR, though only slightly; The fastest of our methods, HCdel, did not have a higher GLR, suggesting that it learned or kept “better” clauses, rather than more clauses.
	Table 3. Measures of search or reasoning rate for the four solvers. Conflicts, Decisions and Propagations are in thousands of events per second.
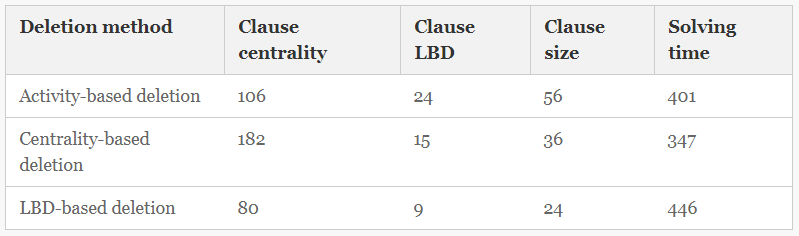
	Learned Clause Quality. Measures of “clause quality” that have been studied or used in solver heuristics include size, literal block distance (LBD) and activity. Here we add clause centrality to these. Small clauses are good because they eliminate many truth assignments and facilitate propagation. Literal Block Distance is defined relative to a CDCL assignment stack, and is the number of different decision levels for variables in the clause. Small LBD clauses are like short clauses relative to assignments that are near the current one [6]. Clause activity is an analog of VSIDS activity, bumped each time the clause is used in a learned clause derivation [28]. Intuitively, clauses with low centrality connect variables “on the edge of the formula”, and a long clause with low centrality connects many such variables, so is likely hard to use.
	To see the effect of centrality-based deletion on clause quality, we measured the quality of learned clauses kept in LOCAL for three deletion schemes: Activity based deletion (default Maple LCM Dist); Centrality-based deletion (HCdel); and LBD-based deletion (implemented in Maple LCM Dist for this study). Table 4 shows the results. Reported numbers are the mean of measurements taken just after each clause deletion phase. We observe:
	Centrality-based deletion keeps better clauses than activity-based deletion, as measured by both size and LBD, and also performs better. LBD-based deletion keeps the “best” clauses measured by LBD and size, has the worst performance and keeps the worst clauses measured by centrality. Centrality is the only clause quality measure that perfectly predicts ordering of the deletion methods by solving speed.
	Table 4.Measures of quality for clauses in the LOCAL clause set, for three deletion schemes. (Centralities are scaled by 10,000).

 

 

6 Discussion

	We introduced four centrality-based modifications to standard CDCL decision and deletion heuristics, and implemented these in Maple LCM Dist, first-place solver from the Main Track of the 2017 SAT Solver Competition. All four changes improved the performance on the formulas from this track.
	The centrality-based deletion scheme, HCdel, solved the most formulas, produced the smallest PAR-2 scores, and also gave the most reliable speed-ups. This deletion scheme is based on clause centrality, a new measure of clause quality introduced here. We presented other evidence that clause centrality is an interesting clause quality measure, and we believe that further study of this measure will be productive.
	The decision heuristic modifications performed less well than HCdel, but confirm the importance of variable centrality, and are interesting because they seem to work for different formulas. For example, among 26 formulas that at least one method solved and at least one did not, there are 12 formulas that are either solved by HCbump-L and no other method, or not solved by HCbump-L but solved by all other methods.
	Work in progress includes more in-depth study of the roles of variable and clause centrality in solver execution, and development of a centrality-based restart strategy.

 

References

1. 1.
   Alekhnovich, M., Razborov, A.A.: Satisfiability, branch-width and Tseitin tautologies. In: 43rd Symposium on Foundations of Computer Science (FOCS 2002), 16–19 November 2002, Vancouver, BC, Canada, pp. 593–603. IEEE (2002)Google Scholar
2. 2.
   Ansótegui, C., Bonet, M.L., Giráldez-Cru, J., Levy, J.: Community structure in industrial SAT instances (2016). arXiv:1606.03329 [cs.AI]
3. 3.
   Ansótegui, C., Giráldez-Cru, J., Levy, J.: The community structure of SAT formulas. In: Cimatti, A., Sebastiani, R. (eds.) SAT 2012. LNCS, vol. 7317, pp. 410–423. Springer, Heidelberg (2012).  https://doi.org/10.1007/978-3-642-31612-8_31CrossRefzbMATHGoogle Scholar
4. 4.
   Ansótegui, C., Giráldez-Cru, J., Levy, J., Simon, L.: Using community structure to detect relevant learnt clauses. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 238–254. Springer, Cham (2015).  https://doi.org/10.1007/978-3-319-24318-4_18CrossRefGoogle Scholar
5. 5.
   Atserias, A., Fichte, J.K., Thurley, M.: Clause-learning algorithms with many restarts and bounded-width resolution. In: Kullmann, O. (ed.) SAT 2009. LNCS, vol. 5584, pp. 114–127. Springer, Heidelberg (2009).  https://doi.org/10.1007/978-3-642-02777-2_13CrossRefzbMATHGoogle Scholar
6. 6.
   Audemard, G., Simon, L.: Predicting learnt clauses quality in modern sat solvers. In: 21st International Joint Conference on Artificial Intelligence, IJCAI 2009, pp. 399–404, San Francisco, CA, USA. Morgan Kaufmann (2009)Google Scholar
7. 7.
   Balyo, T., Heule, M.J.H., Jarvisalo, M.J.: Proceedings of SAT competition 2016. Technical report, University of Helsinki (2016)Google Scholar
8. 8.
   Ben-Sasson, E., Wigderson, A.: Short proofs are narrow - resolution made simple. In: Thirty-First Annual ACM Symposium on Theory of Computing, pp. 517–526. ACM (1999)Google Scholar
9. 9.
   Cedar, A Compute Canada Cluster. https://docs.computecanada.ca/wiki/Cedar
10. 10.
    Compute Canada: Advanced Research Computing (ARC) Systems. https://www.computecanada.ca/
11. 11.
    Fortunato, S.: Community detection in graphs. Phys. Rep. 486(3–5), 75–174 (2010)MathSciNetCrossRefGoogle Scholar
12. 12.
    Freeman, L.C.: A set of measures of centrality based on betweenness. Sociometry 40(1), 35–41 (1977)CrossRefGoogle Scholar
13. 13.
    Gomes, C.P., Selman, B.: Problem structure in the presence of perturbations. In: 14th National Conference on Artificial Intelligence and Ninth Innovative Applications of Artificial Intelligence Conference, (AAAI 1997, IAAI 1997), 27–31 July 1997, Providence, Rhode Island, pp. 221–226. AAAI (1997)Google Scholar
14. 14.
    Jamali, S., Mitchell, D.: Improving SAT solver performance with structure-based preferential bumping. In: 3rd Global Conference on Artificial Intelligence (GCAI 2017), Miami, FL, USA, 18–22 October 2017, vol. 50. EPiC, pp. 175–187. EasyChair (2017)Google Scholar
15. 15.
    Katsirelos, G., Simon, L.: Eigenvector centrality in industrial SAT instances. In: Milano, M. (ed.) CP 2012. LNCS, pp. 348–356. Springer, Heidelberg (2012).  https://doi.org/10.1007/978-3-642-33558-7_27CrossRefGoogle Scholar
16. 16.
    Liang, J.H., Ganesh, V., Poupart, P., Czarnecki, K.: Learning rate based branching heuristic for SAT solvers. In: Creignou, N., Le Berre, D. (eds.) SAT 2016. LNCS, vol. 9710, pp. 123–140. Springer, Cham (2016).  https://doi.org/10.1007/978-3-319-40970-2_9CrossRefzbMATHGoogle Scholar
17. 17.
    Liang, J.H., Ganesh, V., Zulkoski, E., Zaman, A., Czarnecki, K.: Understanding VSIDS branching heuristics in conflict-driven clause-learning SAT solvers. In: Piterman, N. (ed.) HVC 2015. LNCS, vol. 9434, pp. 225–241. Springer, Cham (2015).  https://doi.org/10.1007/978-3-319-26287-1_14CrossRefGoogle Scholar
18. 18.
    Liang, J.H., Hari Govind, V.K., Poupart, P., Czarnecki, K., Ganesh, V.: An Empirical Study of Branching Heuristics Through the Lens of Global Learning Rate. In: Gaspers, S., Walsh, T. (eds.) SAT 2017. LNCS, vol. 10491, pp. 119–135. Springer, Cham (2017).  https://doi.org/10.1007/978-3-319-66263-3_8CrossRefzbMATHGoogle Scholar
19. 19.
    Luo, M., Li, C.-M., Xiao, F., Manyà, F., Lü, Z.: An effective learnt clause minimization approach for CDCL SAT solvers. In: 26th International Joint Conference on Artificial Intelligence (IJCAI 2017), Melbourne, Australia, 19–25 August 2017, pp. 703–711 (2017). ijcai.org
20. 20.
    Martins, R., Manquinho, V., Lynce, I.: Community-based partitioning for MaxSAT solving. In: Järvisalo, M., Van Gelder, A. (eds.) SAT 2013. LNCS, vol. 7962, pp. 182–191. Springer, Heidelberg (2013).  https://doi.org/10.1007/978-3-642-39071-5_14CrossRefGoogle Scholar
21. 21.
    Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: engineering an efficient SAT solver. In: 38th annual Design Automation Conference (DAC 2001), pp. 530–535. ACM (2001)Google Scholar
22. 22.
    NetworkX, Software for complex networks. https://networkx.github.io/
23. 23.
    Neves, M., Martins, R., Janota, M., Lynce, I., Manquinho, V.: Exploiting resolution-based representations for MaxSAT solving. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 272–286. Springer, Cham (2015).  https://doi.org/10.1007/978-3-319-24318-4_20CrossRefGoogle Scholar
24. 24.
    Newsham, Z., Ganesh, V., Fischmeister, S., Audemard, G., Simon, L.: Impact of community structure on SAT solver performance. In: Sinz, C., Egly, U. (eds.) SAT 2014. LNCS, vol. 8561, pp. 252–268. Springer, Cham (2014).  https://doi.org/10.1007/978-3-319-09284-3_20CrossRefzbMATHGoogle Scholar
25. 25.
    Newsham, Z., Lindsay, W., Ganesh, V., Liang, J.H., Fischmeister, S., Czarnecki, K.: SATGraf: visualizing the evolution of SAT formula structure in solvers. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 62–70. Springer, Cham (2015).  https://doi.org/10.1007/978-3-319-24318-4_6
26. 26.
    SAT Competition 2017, July 2017. https://baldur.iti.kit.edu/sat-competition-2017/
27. 27.
    Sonobe, T., Kondoh, S., Inaba, M.: Community branching for parallel portfolio SAT solvers. In: Sinz, C., Egly, U. (eds.) SAT 2014. LNCS, vol. 8561, pp. 188–196. Springer, Cham (2014).  https://doi.org/10.1007/978-3-319-09284-3_14CrossRefzbMATHGoogle Scholar
28. 28.
    Sorensson, N., Een, N.: Minisat v1. 13 - a SAT solver with conflict-clause minimization. In: Poster at the 8th Conference on Theory and Applications of Satisfiability Testing (SAT 2005), St. Andrews, UK, 19–23 June 2005Google Scholar
29. 29.
    Williams, R., Gomes, C.P., Selman, B.: Backdoors to typical case complexity. In: 18th International Joint Conference on Artifical Intelligence (IJCAI 2003) Acapulco, Mexico, 9–15 August 2003, pp. 1173–1178. Morgan Kaufmann (2003)Google Scholar
30. 30.
    Xu, L., Hutter, F., Hoos, H.H., Leyton-Brown, K.: SATzilla: portfolio-based algorithm selection for SAT. J. Artif. Intell. Res. 32, 565–606 (2008)zbMATHGoogle Scholar