The Impact of Branching Heuristics in Propositional Satisfiability Algorithms (1999)
1 Introduction
Propositional Satisfiability (SAT) is a core problem in Artificial Intelligence, as well as in many other areas of Computer Science and Engineering.Recent years have seen dramatic improvements in the real world performance of SAT algorithms。
Recent years have seen dramatic improvements in the real world performance of SAT algorithms。For this purpose we apply different backtrack search SAT algorithms and different branching heuristics to different classes of real-world practical applications of SAT.
. One interesting result of this study is that even though branching heuristics are indeed of importance in solving SAT, other aspects of the organization of backtrack search algorithms turn out to be of far more significance when the objective is to reduce the amount of search and the running time。
本研究的一个有趣的结果是,尽管分支启发法在求解SAT中确实很重要,但当目标是减少搜索量和运行时间时,回溯搜索算法的组织的其他方面变得更加重要。
This empirical result motivates the development of new search pruning techniques, in particular when the objective is to solve large, structured and hard instances of SAT.
译文:这一实证结果推动了新的搜索剪枝技术的发展,特别是当目标是解决大型、结构化和困难的SAT实例时。
本文的行文组织:
标记框架——第2节介绍了本文其余部分使用的标记框架
已有回溯算法——在第3节中,简要回顾了当前最先进的回溯搜索SAT算法。
描述本文中所评估的不同的分支启发法
第5节提供并分析了来自不同应用领域的SAT实例的实验结果。
最后,第六部分对全文进行总结
2 Definitions
3 Backtrack Search SAT Algorithms
This SAT algorithm captures the organization of several of the most competitive algorithms [2, 9, 18, 24]. The algorithm conducts a search through the space of the possible truth assignments to the problem instance variables.译文:该算法对问题实例变量的可能真值分配空间进行搜索。
Preprocess() function —— 化简函数
Decide() function —— 选择决策变元并赋值;
Deduce() function —— BCP的传播函数。译文:隐含的必要赋值由演绎()函数标识,该函数在大多数情况下对应于BCP过程[23]
Diagnose() function —— 冲突分析函数。
The Erase() function —— 回溯函数
Currently, and for solving large, structured and hard instances of SAT, all of the most efficient SAT algorithms implement a number of the following key properties:
译文:目前,为了解决SAT的大型、结构化和硬实例,所有最有效的SAT算法都实现了以下几个关键属性:
(1)The analysis of conflicts can be used for implementing Non-Chronological Backtracking search strategies. Hence, assignment selections that are deemed irrelevant can be skipped during the search [2, 18, 24].——非时序回溯
(2)The analysis of conflicts can also be used for identifying and recording new clauses that denote implicates of the Boolean function associated with the CNF formula. Clause recording plays a key role in recent SAT algorithms, despite in most cases large recorded clauses being eventually deleted [2, 18, 24].——生成学习子句和学习子句规模缩减管理。
(3)Other techniques have been developed. Relevance-Based Learning [2] extends the life-span of large recorded clauses that will eventually be deleted. Conflict-Induced Necessary Assignments [18] denote assignments of variables which are necessary for preventing a given conflict from occurring again during the search.
4 Branching Heuristics
This section describes the branching heuristics that are experimentally evaluated in Section 5. The most simple heuristic is to randomly select one of the yet unassigned variables, and to it assign a randomly chosen value. We shall refer to this heuristic as RAND.
Rand——最简单的启发式方法是随机选择一个尚未分配的变量,并为其分配一个随机选择的值。
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Most, if not all, of the most effective branching heuristics take into account the dynamic information provided by the backtrack search algorithm. This information can include, for example, the number of literals of each variable in unresolved clauses and the relative sizes of the unresolved clauses that contain literals in a given variable.
译文:大多数最有效的分支启发法考虑了回溯搜索算法提供的动态信息。例如,该信息可以包括未解析子句中每个变量的文本数量,以及包含给定变量中文本的未解析子句的相对大小。
In the following sections we describe several branching heuristics which utilize dynamic information provided by the backtrack search SAT algorithm.These heuristics are described in the approximate chronological order in which they have been applied to solving SAT.
译文:在接下来的章节中,我们将介绍几种利用回溯搜索SAT算法提供的动态信息的分支启发法。译文:这些启发法是按照它们被应用于求解SAT的大致时间顺序来描述的。
We should note that additional branching heuristics exist and have been studied in the past. See for example [9, 12, 13] for detailed accounts.译文:我们应该注意到额外的分支启发法的存在,并且在过去已经被研究过。有关详细内容,请参见示例[9,12,13]
几种利用回溯搜索SAT算法提供的动态信息的分支启发法
 |
|
|
 |
 |
5.
 |
 |
 |
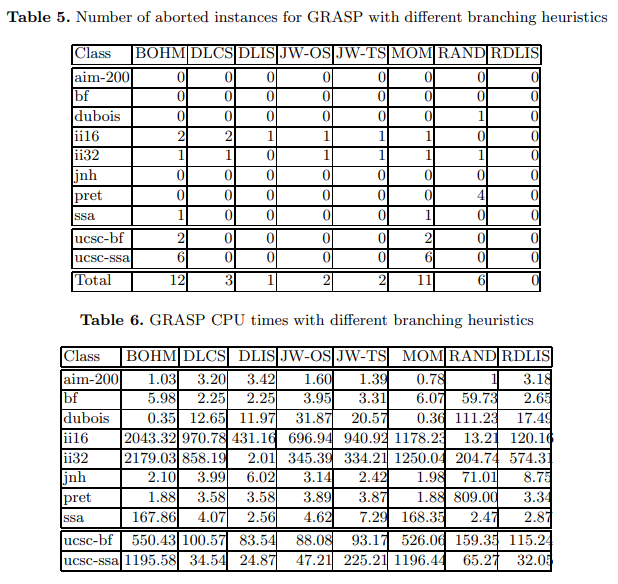
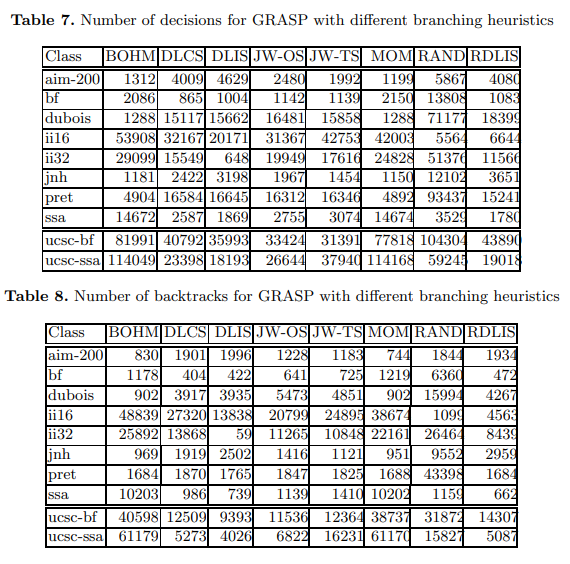
GRASP obtains similar results with most branching heuristics. A more detailed analysis of the experimental data actually reveals substantial differences only for a few instances of the few hundred instances evaluated.
译文:大多数的分支启发法都能得到相似的结果。对实验数据进行更详细的分析实际上发现,在评估的几百个实例中,只有少数几个实例存在重大差异。
– For a few classes of instances, the branching heuristics most often used by SAT algorithms (i.e. BOHM and MOM) end up yielding worse results. Our interpretation is that these heuristics are simply too greedy, and can for some instances make too many bad branches. – The plain, straightforward, randomized branching heuristic, RAND, compares favorably with the other heuristics, and actually performs better (in GRASP and for the classes of instances considered) than BOHM’s or MOM’s heuristics.
– Randomization can actually be a powerful branching mechanism. For example, while DLIS aborts one instance, RDLIS, by not being so greedy as DLIS, aborts none. In general the run times for RDLIS are slightly larger than those for DLIS, but RDLIS is less likely to make bad branches, that can cause a SAT algorithm to eventually quit on a given instance.
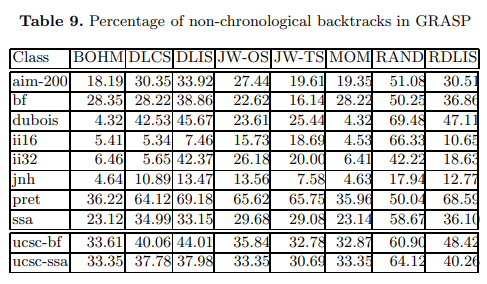
Another interesting result is the percentage of non-chronological backtrack steps (see Table 9). In general the percentages are similar for different heuristics, but differences do exist. Qualitatively, the percentages tend to be similar for three
main groups of heuristics. First for BOHM and MOM, second for DLIS, DLCS, JW-OS, JW-TS, and RDLIS, and finally, for RAND. In general the highest percentage of non-chronological backtrack steps is largest in RAND, which is to be expected.
6.Conclusions
This paper analyzes different backtrack search SAT algorithms and their use of branching heuristics. The obtained experimental results provide evidence that, even though branching heuristics play an important role in solving SAT, more significant performance gains are in general possible, for real-world instances of SAT, by using techniques for pruning the amount of search. Among these, we have studied the effect of non-chronological backtracking and clause recording, among others. Further validation of the conclusions presented in this paper can be obtained by extending the experimental analysis to other real-world applications of SAT, for which relevant sets of instances exist. Techniques for pruning the amount of search have been proposed over the years in many different areas. The results presented in this paper motivate exploring the application of additional search pruning techniques to SAT, with the goal of allowing state-of-the-art SAT algorithms to solve an ever increasing number of real-world instances of SAT.






