Modern CDCL SAT solvers maintain lots of state features such as the partial assignment, trail, learnt clause database, saved phases, etc. 译文:现代CDCL SAT求解器维护了许多状态特性,如部分赋值、跟踪、学习子句数据库、保存阶段等。
Understanding VSIDS Branching Heuristics in Conflict-Driven Clause-Learning SAT Solvers
译文:在使vsid如此有效的过程中,乘法衰减起了什么作用?
译文:我们证明了乘法衰减表现得像指数移动平均线(EMA),它偏爱在冲突中持续出现的变量(信号),而不是间歇出现的变量(噪声)。
译文:vsid是否以时间和空间为焦点。我们表明,与随机分支启发法不同,vsid不成比例地从少数社区中选择变量。
译文:我们把这些发现放在一起,发明了一种新的自适应vsid分支启发法,它解决的问题比2013年SAT竞赛基准中最著名的vsid变体之一还要多。
该算法在代码中的体现可以参见随笔:https://www.cnblogs.com/yuweng1689/p/12695286.html
主要内容:

1 int lbd_val = lbd(learnt_clause); //计算新增学习子句的lbd值 2 lbd_ema = lbd_ema_decay * lbd_ema + (1 - lbd_ema_decay) * lbd_val;//整体LBD的移动平均值 3 if (lbd_val >= lbd_ema) { //第一种情况 4 decays++; //正常普通衰减模式使用次数计数 5 varDecayActivity(var_decay); //正常模式下var_decay为0.85,变元活跃度碰撞增加较快 6 } else { //第二种情况:学习子句lbd低于移动平均 7 thresh_decays++; // 学习子句lbd低于移动平均lbd时,单独计数 8 varDecayActivity(var_thresh_decay); //var_thresh_decay为0.95,变元活跃度碰撞增加较慢 9 } |
2 Background
(1)vsid的分支启发式和变体。
术语vsid指在现代CDCL SAT求解程序中广泛使用的一组分支启发法,这些启发法在求解程序运行期间对布尔公式的所有变量进行排序。就目前的情况来看,VSIDS明显比其他著名的启发式方法更有效,如DLIS[33]、MOM[18]、Jeroslow-Wang[28]和BOHM[12]。VSIDS最初作为箔条解决程序[36]的一部分引入时是一个重大突破。关键的思想是收集对所学从句的统计信息,以指导搜索的方向,在哪里最近学过的从句是受欢迎的。VSIDS的关键特性是加性碰撞和乘性衰变行为,具体描述如下。vsid的另一个优点是计算开销低。我们主要关注vsid的两个比较著名的变体,即Chaff[36]的变体和miniat 2.2.0[15]的变体。我们将这些变体分别称为cVSIDS和mVSIDS。这两种变体都具有下面列出的共同特征。
VSIDS的共同特征 ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Activity Score, Initialization and VSIDS Ranking. VSIDS assigns a floating point number, called activity, to each variable in the Boolean formula. At the begining of a run of a solver, the activity scores of all variables are typically initialized to 0. We refer to the ranking of variables according to their activity scores in the decreasing order as the VSIDS ranking. VSIDS picks the variable with the highest activity to branch on.
译文:活动评分、初始化和vsid排名。VSIDS为布尔公式中的每个变量分配一个称为活动的浮点数。在求解程序开始运行时,所有变量的活动得分通常初始化为0。我们将变量按照其活动得分的降序排序称为VSIDS排序。VSIDS选择活动最高的变量作为分支。
Additive Bump and Multiplicative Decay. When the solver learns a clause, a set of variables is chosen, and their activities are additively increased, typically by 1. The quantum of this increase is called the (additive) bump. At regular intervals during the run of the solver, the activities of all variables are multiplied by a constant 0<α<10<α<1 called the (multiplicative) decay factor.
译文:加法碰撞和乘法衰变。当求解器学习一个子句时,会选择一组变量,并且它们的活动会增加,通常是增加1。译文:这种增加的量称为(附加的)增加。在解算器的运行,定期的活动所有变量乘以一个常数0 <α< 1(乘法)衰减系数。
Chaff中VSIDS的变体:cVSIDS -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
cVSIDS. The activities of variables occurring in the newest learnt clause are bumped up by 1, immediately after the clause is learnt. The activities of all variables are multiplied by a constant 0<α<10<α<1. The decay occurs after every i conflicts. We follow the policy used in recent solvers like MiniSAT and use i=1.
264 void Solver::analyze(CRef confl, vec<Lit>& out_learnt, int& out_btlevel) |
| 在分析函数analyze中得到学习子句后,对分析得到学习子句的每一个变元碰撞得分。 |
miniat 2.2.0VSIDS的变体:mVSIDS --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
mVSIDS. The activities of all variables resolved during conflict analysis that lead to the learnt clause (including the variables in the learnt clause) are bumped up by 1. The activities of all variables are decayed as in cVSIDS.
264 void Solver::analyze(CRef confl, vec<Lit>& out_learnt, int& out_btlevel) 265 { 267 int pathC = 0; 268 Lit p = lit_Undef; 269 270 // Generate conflict clause: 271 // 272 out_learnt.push(); // (leave room for the asserting literal) 273 int index = trail.size() - 1; 274 275 do{ 276 assert(confl != CRef_Undef); // (otherwise should be UIP) 277 Clause& c = ca[confl]; 278 279 if (c.learnt()) 280 claBumpActivity(c); 281 282 for (int j = (p == lit_Undef) ? 0 : 1; j < c.size(); j++){ 283 Lit q = c[j]; 284 285 if (!seen[var(q)] && level(var(q)) > 0){ 286 varBumpActivity(var(q)); 287 seen[var(q)] = 1; 288 if (level(var(q)) >= decisionLevel()) 289 pathC++; 290 else 291 out_learnt.push(q); 292 } 293 } 294 295 // Select next clause to look at: 296 while (!seen[var(trail[index--])]); 297 p = trail[index+1]; 298 confl = reason(var(p)); 299 seen[var(p)] = 0; 300 pathC--; 301 302 }while (pathC > 0); 303 out_learnt[0] = ~p; 304 305 // Simplify conflict clause: 306 // 307 int i, j; 308 out_learnt.copyTo(analyze_toclear); 309 if (ccmin_mode == 2){ 310 uint32_t abstract_level = 0; 311 for (i = 1; i < out_learnt.size(); i++) 312 abstract_level |= abstractLevel(var(out_learnt[i])); 312 314 for (i = j = 1; i < out_learnt.size(); i++) 315 if (reason(var(out_learnt[i])) == CRef_Undef || !litRedundant(out_learnt[i], abstract_level)) |
| 在分析函数analyze中,在蕴含图蕴含点切割时,对参与构成学习子句的路径上的变元及其所在子句中的其它变元碰撞得分。 |
Variable Incidence Graph (VIG)
vertices of the graph are the variables in the formula. For every clause c∈Fc∈F we have an edge between each pair of variables in c. In other words, each clause corresponds to a clique between its variables. The weight of an edge is 。。。
where |c| is the length of the clause. VIG does not distinguish between positive and negative occurrences of variables. We combine all edges between each pair of vertices into one weighted edge by summing the weights. More precisely, the VIG of a CNF formula F is a weighted graph defined as follows: set of vertices V=VarV=Var, set of edges 。。。, and the weight function w(xy) 。。。

3 Contribution I and II: Community-Focused Search, Bridge Variables, and VSIDS
The Hypotheses.
Here we state the three hypotheses that we tested in this section: (1) Bridge Experiment: VSIDS disproportionately picks, bumps, and learns the bridge variables, (2) Spatial Focus Experiment: VSIDS disproportionately picks from a smaller number of communities rather than a large fraction of the communities of a SAT instance, and (3) Temporal Focus Experiment: VSIDS typically picks from recently-seen communities.
三个假设:(1)桥梁实验:vsid不成比例地选择、碰撞和学习桥接变量;
(2)空间聚焦实验:VSIDS不成比例地从更少的社区中选择,而不是从SAT实例的大部分社区中选择;
(3)时间焦点实验:vsid通常从最近看到的社区中挑选。
Results and Interpretations of Bridge Variable Experiment.
 |
 |
Recent research suggests that CDCL solvers take advantage of good community structure in SAT instances [38] leading to faster solving time. The reason for this phenomenon is not fully understood. One possibility is that good community structure lends itself to divide-and-conquer because the bridges are easier to cut (i.e., satisfy). More precisely, the solver can focus its attention on the bridges by picking the bridge variables and assigning them appropriate values. When it eventually assigns the correct values to enough bridges, the VIG is divided into multiple components, and each component can be solved with no interference from each other. Even if the VIG cannot be completely separated, it may still be beneficial to the cut bridges between communities so that these communities can be solved relatively independently.
关于表1——最近的研究表明,CDCL求解者在SAT实例[38]中利用了良好的社区结构,从而加快了求解时间。一种可能性是,良好的社区结构有助于分治,因为桥梁更容易被切断(即,社区结构更容易被破坏,满足) 。 更准确地说,求解器可以通过选择桥接变量并为它们分配适当的值来将注意力集中在桥接上。当它最终将正确的值分配给足够多的桥时,VIG被划分为多个组件,并且每个组件可以在互不干扰的情况下解决。即使VIG不能完全分离,它仍然可能有利于社区之间的桥梁,使这些社区可以相对独立地解决。
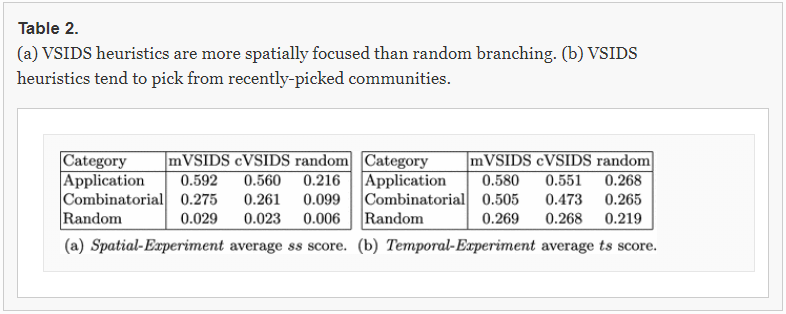
关于表2——
Results and Interpretations of Temporal and Spatial Focused Search Experiments. Table 2a depicts the average Gini coefficient for the Spatial-Experiment. Both VSIDS techniques exhibit much more inequality relative to random branching for the application and combinatorial instances, indicating that VSIDS may be attempting to hone in on certain communities.
译文:表2a描述了空间实验的平均基尼系数。与应用程序的随机分支和组合实例相比,这两种VSIDS技术表现出更多的不平等,这表明VSIDS可能试图在某些社区进行磨练。
The very low values for random instances indicate that none of the branching heuristics typically favor certain communities, likely due to the poor community structures exhibited by such instances.
译文:随机实例的非常低的值表明,没有一个分支启发法通常支持特定的社区,这可能是由于此类实例所显示的糟糕的社区结构。
Table 2b demonstrates that VSIDS techniques are much more temporally focused on average than random branching. It is commonly believed that VSIDS improves the search locality [32, 37] which in turn improves solver performance. However, this term search locality has previously been not rigorously defined. We precisely defined spatial focus and temporal focus, and show that VSIDS displays high search locality in terms of these definitions.
表2b表明VSIDS技术比随机分支更侧重于平均时间;通常认为VSIDS改善了搜索的局部性[32,37],这反过来又改善了求解器的性能;然而,这个本地搜索术语以前没有严格定义。我们精确地定义了空间焦点和时间焦点,并证明了vsid在这些定义中显示了较高的搜索局部性。
4 Contribution III: Experimental Evidence Supporting Strong Correlation Between TGC and VSIDS
In this section, we describe the experiments to support the hypothesis that the VSIDS variants cVSIDS and mVSIDS, viewed as ranking functions, correlate strongly with both temporal degree centrality and temporal eigenvector centrality according to Spearman’s rank correlation coefficient and top-k measures. Combining the results of this section with Contribution I (namely, VSIDS picks, bumps and learns over bridge variables), we conclude that VSIDS picks high-centrality bridge variables.
译文:在本节中,我们根据Spearman的秩相关系数和top-k测度描述了支持VSIDS变式cVSIDS和mVSIDS作为排序函数与时间度中心性和时间特征向量中心性强相关这一假设的实验。
译文:结合本节的结果和贡献I(即VSIDS挑选、碰撞和学习桥接变量),我们得出结论:VSIDS挑选高中心性桥接变量。
(1) temporal variable incidence graph (TVIG) 时间变量关联图
In the TVIG, every clause is labeled with a timestamp denoted t(c). The t(c) is equal to 0 if c is a clause from the original input formula, otherwise t(c) is equal to the number conflicts up to the learning of c. 原始子句的时间戳为0;学习子句的时间戳为生成该子句时刻求解冲突数。
We refer to the difference between the current time t and the timestamp of a clause t(c) as the age of the clause:
age(c) = t-t(c) |
我们将当前时间t与子句t(c)的时间戳之间的差异称为子句的年龄。
\frac{\alpha ^{age(e)}}{|c|-1}
|
More precisely, the TVIG of a clause database at time t is defined in the same way as VIG except with a modified weight function that takes the ages of clauses into account:译文:更准确地说,一个子句数据库在t时刻的TVIG的定义方法与VIG相同,只是添加了一个修改后的权函数,该函数将子句的年龄考虑在内:
w(xy) = \sum _{x,y\in c \in F} \frac{\alpha ^{age(c)}}{|c|-1}
|
Observe that the TVIG evolves throughout the solving process: as new learnt clauses are added, new edges are added to the graph, and all the ages increase. As an edge’s age increases, its weight decreases exponentially with time assuming no new learnt clause contains its variables. In many domains, it is often the case that more recent data points are more useful than older data points.
译文:观察TVIG在整个解决过程中的演变:随着新的习得子句的添加,新的边被添加到图中,所有的年龄都增加了。当一个边的年龄增长,它的重量指数下降(与时间假设没有新的学习子句包含它的变量相比较)。译文:在许多领域,经常出现这样的情况,即最近的数据点比旧的数据点更有用。
(2)graph centrality measure 图中心性度量是一个函数,它为图中的每个顶点分配一个实数。
A graph centrality measure is a function that assigns a real number to each vertex in a graph. The number associated with each vertex denotes its relative importance in the graph [16, 19, 41]. For example, the degree centrality [16] of a vertex in a graph is defined as the degree of the vertex.
译文:图中心性度量是一个函数,它为图中的每个顶点分配一个实数。与每个顶点相关的数字表示其在图中的相对重要性[16,19,41]。例如,图中顶点的度中心性[16]被定义为顶点的度。
The eigenvector centrality of a vertex in a graph is defined as its corresponding value in the eigenvector of the greatest eigenvalue of the graph’s adjacency matrix. We similarly define the temporal versions of degree and eigenvector centrality. The key idea needed to define temporal graph centrality measures is to incorporate temporal information inside the TVIG.
译文:图中顶点的特征向量中心性定义为图的邻接矩阵的最大特征值的特征向量中对应的值。我们同样定义了度和特征向量中心性的时间版本。定义时间图中心性度量所需要的关键思想是将时间信息合并到TVIG中。
The temporal degree centrality (TDC) ——时间程度中心性(TDC)
temporal eigenvector centrality (TEC)——时间特征向量中心性 (TEC) t时刻TVIG中顶点的特征向量中心性
(3)Methodology for Comparing Rankings based on Spearman’s Rank Correlation Coefficient.基于斯皮尔曼等级相关系数的排名比较方法。
It is commonly believed that VSIDS focuses on the “most constrained part of the formula” [24], and that this is responsible for its effectiveness.
译文:一般认为,VSIDS侧重于“公式中最受约束的部分”[24],这是其有效性的原因。
However, the term “most constrained part of the formula” has previously not been well-defined in a mathematically precise manner.
译文:然而,“公式中最受约束的部分”这个术语以前并没有以精确的数学方式定义。
译文:定义变量约束的一种直观方法是分析布尔公式,并计算一个变量在多少个子句中出现。
译文:然后,可以根据这个指标对变量进行排序。事实上,这种方法是分支启发法DLIS[33]的基础,曾经是SAT求解器中占主导地位的分支启发法。
7 Interpretation of Results
(1)What is special about the class of variables that VSIDS chooses to additively bump? 译文:vsid选择的这类变量有什么特别之处?
In the VSIDS vs. TGC experiments (Sect. 4), we used the Spearman’s rank correlation coefficient to show that the VSIDS and TGC rankings are strongly correlated.
译文:在VSIDS与TGC的实验中(第4节),我们使用Spearman的等级相关系数来表明VSIDS与TGC的等级具有很强的相关性。
From our experiments, we can say that for all the VSIDS variants considered in this paper, additive bumping matches with the increase in centrality of the chosen variables.
译文:从我们的实验中可以看出,对于本文考虑的所有VSIDS变量,加性凸点都与所选变量中心性的增加相匹配。
We also observe from our results that the variables that solvers pick for branching have very high TGC rank. The concept of centrality allows us to define in a mathematically precise the intuition many solver developers have had, i.e., that branching on “highly constrained variables” is an effective strategy.
译文:我们还从结果中观察到,求解者为分支选择的变量具有非常高的TGC秩。中心性的概念允许我们以精确的数学方式定义许多求解程序开发人员具有的直觉,即,在“高度约束变量”上进行分支是一种有效的策略。
Our bridge variable experiment combined with the TGC experiment suggests that VSIDS focuses on high-centrality bridge variables.
译文:我们的桥梁变量实验结合TGC实验表明,vsid侧重于高中心性桥梁变量。
8 Related Work
Marques-Silva and Sakallah are credited with inventing the CDCL technique [34]. The original VSIDS heuristic was invented by the authors of Chaff [36].
Armin Biere [8] described the low-pass filter behavior of VSIDS, and Huang et al. [26] stated that VSIDS is essentially an EMA.
译文:Armin Biere[8]描述了VSIDS的低通滤波行为,Huang等人[26]认为VSIDS本质上是EMA(指数移动平均)
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Katsirelos and Simon [30] were the first to publish a connection between eigenvector centrality and branching heuristics. In their paper [30], the authors computed eigenvector centrality (via Google PageRank) only once on the original input clauses and showed that most of the decision variables have higher than average centrality.
译文:Katsirelos和Simon[30]首先发表了特征向量中心性和分支启发法之间的联系。
译文:作者对原始输入子句仅计算了一次特征向量中心性(通过谷歌PageRank),结果表明大多数决策变量的中心性高于平均中心性。
Also, it bears stressing that their definition of centrality is not temporal. By contrast, our results correlate VSIDS ranking with temporal degree and eigenvector centrality, and show the correlation holds dynamically throughout the run of the solver.
译文:此外,它还需要强调,它们对中心性的定义不是暂时的。
译文:我们的结果将vsid排序与时间度和特征向量的中心性联系起来,并在整个求解过程中动态地展示了相关性。
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Also, we noticed that the correlation is also significantly stronger after extending centrality with temporality. Simon and Katsirelos do hypothesize that VSIDS may be picking bridge variables (they call them fringe variables). However, they do not provide experimental evidence for this.
译文:此外,我们注意到,在将中心性与时间性延长后,相关性也显著增强。Simon和Katsirelos假设vsid可能会选择桥接变量(他们称之为边缘变量)。然而,他们并没有为此提供实验证据。
To the best of our knowledge, we are the first to establish the following results regarding VSIDS: first, VSIDS picks, bumps, and learns high-centrality bridge variables; second, VSIDS-influenced search is more spatially and temporally focused than other branching heuristics we considered; third, explain the importance of EMA (multiplicative decay) to the effectiveness of VSIDS; and fourth, invent a new adaptive VSIDS branching heuristic based on our observations.
译文:据我们所知,我们首先确定了关于vsid的下列结果:
译文:首先,vsid挑选、颠簸和学习高中心性桥接变量;
译文:其次,与我们考虑的其他分支启发法相比,受vsid影响的搜索更关注空间和时间;
译文:第三,解释EMA(乘法衰减)对vsid有效性的重要性(本质上是指数平滑的一种形式);
译文:基于我们的观察,发明一种新的自适应vsid分支启发法。





