文献学习——Evaluating CDCL Variable Scoring Schemes
作者:Armin Biere ( B ) and Andreas Fröhlich ------大牛,CaDiCal、YalSAT、Lingeling等求解器的研发团队负责人
这是作者2015年发表的文献,其中深入讲解了VMTF。该技术目前是应用求解unsat样例最有效,能多求出近10个。
VMTF最早见文献:
Ryan, L.: Efficient algorithms for clause-learning SAT solvers. Master’s thesis,
Simon Fraser University (2004)
Abstract.
The VSIDS (variable state independent decaying sum) decision heuristic invented in the context of the CDCL (conflict-driven clause
learning) SAT solver Chaff, is considered crucial for achieving high efficiency of modern SAT solvers on application benchmarks.
译文:VSIDS(可变状态独立衰减和)决策启发法是在冲突驱动子句学习SAT求解器的背景下发明的,它被认为是实现现代SAT求解器在应用基准上的高效率的关键。
This paper proposes ACIDS (average conflict-index decision score), a variant of VSIDS. The ACIDS heuristics is compared to the original implementation of VSIDS, its popular modern implementation EVSIDS (exponential VSIDS), the VMTF (variable move-to-front) scheme, and other related decision heuristics.
译文:本文提出了一种改进的方案——平均冲突指数决策得分。将ACIDS的启发法与vsid的原始实现进行比较,后者是流行的现代实现EVSIDS(指数级) VSIDS)、VMTF(变量前移)方案以及其他相关的决策启发法。
They all share the important principle to select those variables as decisions, which recently participated in conflicts. The main
goal of the paper is to provide an empirical evaluation to serve as a
starting point for trying to understand the reason for the efficiency of these decision heuristics.
译文:它们都有一个重要的原则,即选择那些最近参与冲突的变量作为决策。本文的主要目的是提供一个经验评估,作为一个起点,试图了解这些决策启发的效率的原因。
In our experiments, it turns out that EVSIDS, VMTF, ACIDS behave very similarly, if implemented carefully.
译文:在我们的实验中,结果表明EVSIDS、VMTF和酸的行为非常相似,如果仔细实施的话。
1 Introduction
VSIDS ----- variable state independent decaying sum (VSIDS) decision heuristic。
Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: engi-
neering an efficient SAT solver. In: Proceedings of the 38th Design Automation
Conference, DAC 2001, pp. 530–535. ACM, Las Vegas, June 18–22, 2001
EVSIDS ------- exponential VSIDS (EVSIDS)
Biere, A.: Adaptive restart strategies for conflict driven SAT solvers. In: Kleine
Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 28–33. Springer,
Heidelberg (2008)
The EVSIDS heuristic allows fast
selection of decision variables and adds focus to the search, but also is able to pick
up long-term trends due to a “smoothing” component, as argued in [6].
译文:EVSIDS启发式允许快速选择决策变量,并将重点添加到搜索中,但也能够通过“平滑”组件获取长期趋势,如[6]中所述。
On the practical side, there have been various attempts to improve on the
EVSIDS scheme. These include the variable move-to-front (VMTF) strategy
of the Siege SAT solver [8], the BerkMin strategy [9], which is focusing on
recently learned clauses, and the clause move-to-front (CMTF) strategies of
HaifaSAT [10] and PrecoSAT [11].
译文:在实践方面,已经有各种改进的尝试EVSIDS方案。这些策略包括围攻SAT解算器[8]的可变移动到前线(VMTF)策略,BerkMin策略[9],它关注于最近学习的子句,以及子句移动到前线(CMTF)策略HaifaSAT[10]和PrecoSAT[11]。
VMTF ------ variable move-to-front (VMTF) strategy
Ryan, L.: Efficient algorithms for clause-learning SAT solvers. Master’s thesis,
Simon Fraser University (2004)。
CMTF ------- the clause move-to-front (CMTF) strategie
对应于两类求解器HaifaSAT [10] and PrecoSAT [11]
ACIDS ------ 本文提出的策略 average conflict-index decision score (ACIDS)
2.Decision Heuristics
本节将变元决策各种策略的来龙去脉讲的非常清楚。
知识点1:决策启发式可以转变为变量选择启发式
Modulo initialization, typically based on (one-sided)
Jeroslow-Wang’s heuristic [20], phase saving turns the decision heuristic into a
variable selection heuristic.
译文:模块化初始化、通常基于(单侧)Jeroslow-Wang的启发式[20]和相位保持三项技术的成熟,使得决策启发式可以转变为变量选择启发式。
Accordingly, we focus on variable selection, which in
turn will be based on selecting a variable with the highest decision score.
译文:因此,我们将重点放在变量选择上,而变量选择将基于选择具有最高决策得分的变量
知识点2:
The original VSIDS implementation in Chaff
worked as follows:
Variables are stored in an array used to search for a decision
variable. After learning a clause, the score of its variables is incremented. Further,
every 256th conflict, all variable scores are divided by 2, and the array is sorted
w.r.t. decreasing score.
译文:变量存储在一个数组中,用于搜索决策变量。在学习了一个子句之后,构成学习子句的变量得分会增加。此外,每256次冲突,所有变量得分除以2,数组按w.r.t递减排序。
The process of updating scores of variables is also referred to as variable bumping [7].
Note, however, that in modern solvers and also in our experiments
we not only bump variables of the learned clause, but all seen variables occur-
ring in antecedents used to derive the learned clause through a regular input
resolution chain [25] from existing clauses.
译文:然而,请注意,在现代的求解程序中,以及在我们的实验中,我们不仅碰撞了习得子句的变量,而且所有可见的变量都发生了—通过现有子句的常规输入解析链[25]派生习得子句的先行词中的环
An essential optimization in Chaff
is to cache the position of the last found decision variable with maximum score
in the ordered array.
译文:Chaff的一个基本优化是将最后一个找到的决策变量的位置与最大得分一起缓存到有序数组中。
知识点3:
增加变量得分与增加学习子句参与冲突索引的次数
INC (or inc in the experiments)
SUM (or sum in our experiments)
The decide procedure selects the next decision variable, by searching for the
first unassigned variable in the ordered array, starting at the lower end, e.g., the
variable with the highest score during sorting.
译文:decide过程通过在有序数组中搜索第一个未赋值的变量来选择下一个决策变量,从低端开始,例如排序过程中得分最高的变量。
An essential optimization in Chaff
is to cache the position of the last found decision variable with maximum score
in the ordered array. This position is used as starting point for the next search.
译文:Chaff的一个基本优化是将最后一个找到的决策变量的位置与最大得分一起缓存到有序数组中。此位置用作下一次搜索的起点。
If a variable in the array with a position smaller than the cached maximum score
position becomes unassigned then the maximum score position is updated to
that position. During rescoring, similar updates might be necessary.
译文:如果数组中位置小于缓存的最大得分位置的变量未被赋值,则最大得分位置将被更新到该位置。在重新计分时需要进行更新操作。
The first part of VSIDS, e.g., only incrementing scores, constitutes an approximation of dynamic DLIS. It counts occurrences of variables in clauses, ignoring whether a clause is satisfied or not, or even removed during learned clause deletions [3] (called clause database reduction in the following). 译文:vsid的第一部分,例如,只增加分数,构成动态DLIS的近似。它计算子句中变量的出现次数,忽略是否满足子句。(在学习子句删除策略时也是不考虑被删除的学习自己是否满足的。学习子句删除在后面我们统称“学习子句数据库缩减”)。
This restricted version of VSIDS without smoothing is denoted INC (or inc in the experiments).译文:这种没有平滑的vsid的受限版本被称为INC(或实验中的INC)。
As an alternative to using frequent rescoring, we propose that the smoothing
part of VSIDS can also be approximated by adding the conflict-index to the score
instead of just incrementing it.
译文:作为使用频繁重新计分的一种替代方法,我们建议vsid的平滑部分也可以通过将冲突索引添加到分数中来近似化,而不是仅仅增加它。
The conflict-index is the total number of conflicts
that occurred so far. We call this scheme SUM (or sum in our experiments).
译文:冲突索引是迄今为止发生的冲突总数。我们把这个方案称为和(或在我们的实验中称为和)。
知识点4:EVSIDS.
知识点5:VMTF
知识点6:ACIDS
3.重点学习VMTF
(1)简要介绍
Variable selection heuristics can be seen as online sorting algorithms of variable scores.
译文:变量选择启发式可以看作是变量得分的在线排序算法。
This view suggests to use online algorithms with efficient amortized complexity, such as move-to-front (MTF) [30].
译文:该观点建议使用具有有效平摊复杂度的在线算法,如移动到前面(MTF)
A similar motivation was given in the master thesis of Lawrence Ryan [8], which precedes MiniSAT [7] and
introduced the Siege SAT solver as well as the variable move-to-front (VMTF, or
vmtf in the experiments) strategy.
译文:Lawrence Ryan[8]的硕士论文也给出了类似的动机,该论文先于miniat[7],并引入了围攻求解器和变量移动到前线(VMTF,或实验中的VMTF)策略。
As in Chaff, the restriction in Siege’s VMTF bumping scheme was to only move variables in the learned clause.
译文:在Chaff中,Siege的VMTF碰撞方案的限制是只移动学习子句中的变量。
(注:已经下载有2019年sat竞赛Zchaff版本,参加开发者主页:http://www.princeton.edu/~chaff/people.html )
Actually, only a small subset of those variables, e.g., of size 8, was selected, according to [8].
译文:实际上,根据[8],只选择了这些变量中的一小部分,例如大小为8的变量。
The restriction in Siege to move only a small subset of variables might have
been partially motivated by the cost of moving many.
译文:在这个Siege版本的求解器中,只移动一小部分变量的限制可能部分是由移动许多变量的成本引起的。
It is not uncommon that tens of thousands variables occur in antecedents of a learned clause, which also
are rather long for some instances.
译文:数以万计的变量出现在一个习得子句的先行词中并不罕见,在某些情况下,这些先行词也相当长。
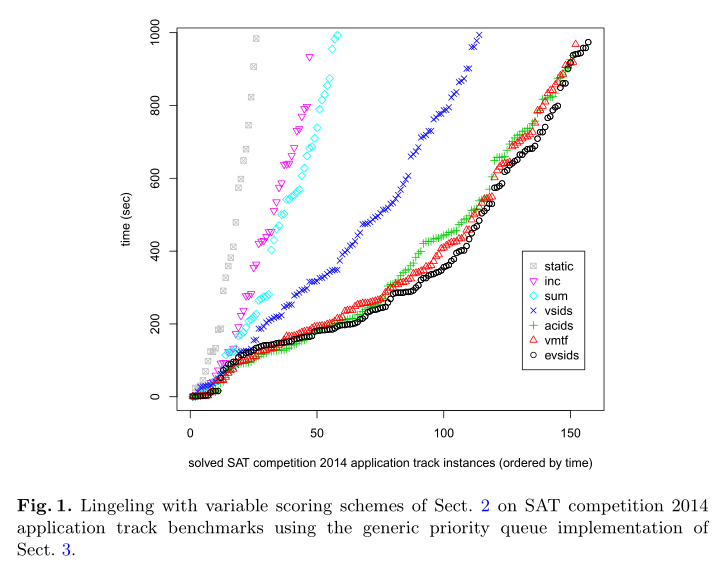
In our experiments in Sect. 4, the default decision heuristic (evsids in Tab. 2) bumped on average 276 literals per learned
clause of average length 105 (on 275 considered instances).
译文:在我们第4节的实验中,默认决策启发式(表2中的evsid)在平均长度为105(在275个考虑的实例中)的每个学习子句中平均替换276个文本。
Unfortunately, details on how even this restricted version of VMTF is implemented in Siege were not
provided. The source code is not available either. We give details for a fast
implementation of unrestricted VMTF in Sect. 3.
译文:不幸的是,关于VMTF的这个受限版本是如何在Siege中实现的细节并没有提供。源代码也不可用。我们在第三节中给出了快速实现无限制VMTF的细节。
(2)实现细节
We describe how the VMTF scheme can be implemented efficiently, as well as
how these techniques can be lifted to implement a generic priority queue, which
(empirically) is efficient for all the considered scoring schemes.
译文:
我们描述了如何有效地实现VMTF方案,以及如何使用这些技术来实现通用优先级队列(经验上)对于所有考虑的评分方案都是有效的。
This new implementation of a priority queue for variable selections combines ideas originally
implemented in Chaff [5] and JeruSAT [29], but adds additional optimizations and works with arbitrary precise floating-point scores, in contrast to an imprecise earlier version implemented in Lingeling [31].
译文:这种新的优先级队列变量选择的实现结合了最初在Chaff[5]和JeruSA29]中实现的思想,但是增加了额外的优化,可以使用任意精确的浮点分数,这与之前在Lingeling[31]中实现的不精确的版本形成了对比。
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Variable scores play a role while (a) bumping variables participating in deriving a learned clause, (b) deciding or searching for the next decision variable, (c)
unassigning variables during backtracking, (d) rescoring variable scores either for explicit smoothing in VSIDS or due to protecting scores from overflow dur-
ing bumping, and (e) comparing past decisions on the trail to maximize trail reuse [28].
译文:变量得分而发挥作用(a)碰撞变量参与推导了学习子句,(b)决定或寻找下一个决策变量,(c)在回溯unassigning变量,d)改成绩显式平滑的vsid或由于溢出保护成绩大调的- ing碰撞,和(e)比较过去决策追踪最大化重用[28]。(是否可以交互用在SLS求解器之中?)
First, we explain a fast implementation for VMTF, focusing on (a)-(c). Next, we address its extension to precise scoring schemes using floating-point
numbers, which in previous implementations followed the example set by MiniSAT to use a binary heap data structure. Last, we discuss (d) and (e).
译文:首先,我们解释了VMTF的一个快速实现,重点是(a)-(c)。
译文:接下来,我们将其扩展为使用浮点数的精确计分方案,在以前的实现中,它遵循了由minisat设置的使用二进制堆数据结构的示例。
译文:最后,我们讨论(d)和(e)。
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
3.1 Fast Queue for VMTF
According to Sect. 2, the score of a variable in VMTF is the conflict-index, e.g.,the number of conflicts at the point a variable was last bumped.
译文:VMTF中变量的得分是冲突索引,例如,在变量最后一次被碰撞时的冲突数。
With this score definition, VMTF can be simulated with a binary heap.
译文:有了这个分数定义,就可以用二进制堆来模拟VMTF。
However, every bump then needs a logarithmic number of steps to “bubble-up” a bumped variable in the heap.
译文:然而,每一次碰撞都需要计算步数的对数值,用该值来“起泡”堆中的碰撞变量。
Instead, a queue, implemented as doubly linked list which holds all variables, only requires two simple constant time operations for bumping:
dequeue the variable and enqueue it back at the end of the list, which we consider
as head. Even storing the score seems to be redundant.
译文:将队列实现为包含所有变量的双链表,只需要两个简单的常量时间操作就可以进行碰撞:将变量从队列中取出,并将其重新放入列表的末尾,我们将其视为head。
译文:甚至存储分数似乎也是多余的。
To find the next decision variable in the queue, we could start at the end (head) of the queue and traverse it backwards until an unassigned variable is found.
译文:要找到队列中的下一个决策变量,我们可以从队列的末尾(头)开始,然后向后遍历它,直到找到未分配的变量为止。
Unfortunately, this algorithm has quadratic accumulated complexity.
译文:不幸的是,该算法具有二次累积复杂度
For example, consider an instance with 10000 variables and a single clause containing all variables in default phase.
译文:例如,考虑一个包含10000个变量和一个包含默认相位所有变量的子句的实例。
However, we can employ the same 2 optimization as used in Chaff (see Sect. 2) and remember the variable up to which the last search
proceeded until finding an unassigned variable.
译文:我们可以使用与在Chaff中使用的相同的2优化(参见第2节),并记住最后一次搜索所使用的变量,直到找到一个未分配的变量为止。
Since the solver will restart the next search at this variable, we call this reference next-search.
译文:由于求解程序将在此变量处重新启动下一个搜索,因此我们将此引用称为下一个搜索(即:下一个搜索位)。
During backtracking, variables are unassigned and (as in Chaff) next-search
potentially has to be updated to such an unassigned variable if it sits further
down the queue closer to head than the next-search variable.
译文:在回溯过程中,变量是未赋值的,并且(在Chaff中)下一个搜索可能必须更新为这样一个未赋值的变量,如果它比下一个搜索变量位于队列更靠前的位置。
备注:
But in reverse order, e.g., while we prefer the variable with largest score at the end
of the queue, Chaff had the variable with largest score at the first array position.
译文:但是以相反的顺序,例如,当我们更喜欢在队列末尾得分最大的变量时,Chaff选择在第一个数组位置得分最大的变量
In order to achieve this, we could use the scores of the variables for comparing queue position.
译文:为了实现这一点,我们可以使用变量的得分来比较队列位置。
However, in VMTF, variables bumped at the same conflict all get the same score,
and thus simply using the score leads to violation of the following important
invariant: variables right of next-search (closer to head) are assigned.
译文:在VMTF中,在同一冲突中被碰撞的变量都得到相同的分数,因此简单地使用分数会导致违反以下重要的不变量:分配变量的下一个搜索权(更靠近头部)。
To fix this problem, we globally count enqueue operations to the queue with an enqueue-counter and remember with each variable the value of the enqueue-
counter at the point the variable was enqueued as enqueue-time.
译文:为了解决这个问题,我们全局地使用一个enqueue-counter将enqueue操作计数到队列中,并记住每个变量在变量被加入队列时的enqueue-counter值为enqueue-time。
Thus, the enqueue-time precisely captures the order of the elements in the queue and can
be used to precisely compare the relative positions of variables in the queue.
译文:因此,enqueue-time可以精确地捕获队列中元素的顺序,并且可以用来精确地比较队列中变量的相对位置。
In the actual implementation, we use a 32-bit integer for the enqueue-counter, which occasionally, e.g., after billion enqueue operations, requires to reassign
enqueue-times to all queue elements in a linear scan of the queue.
译文:
在实际的实现中,我们使用一个32位的整数作为队列计数器,有时候,例如在执行了十亿个队列操作之后,需要重新分配队列线性扫描中所有队列元素的排队时间。
Note that, in a dedicated queue implementation for VMTF (like queue in our experiments),
the scores become redundant again, after adding enqueue-times.
译文:注意,在VMTF的专用队列实现中(如我们的实验中的队列),在添加了排队时间之后,分数再次变得冗余。
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
3.2 Generic Queue for all Decision Heuristics 译文:用于所有决策启发的通用队列
For other schemes, it is tempting to also just use a queue implemented as doubly
linked list as for VMTF, maintaining both scores and enqueue-times.
译文:对于其他方案,也很容易使用与VMTF一样以双链表形式实现的队列,同时维护分数和排队时间。
Every operation remains constant time except for bumping. We have to ensure that
the queue is sorted w.r.t. score.
译文:除了碰撞外,每次操作的时间都保持不变。我们必须确保队列是按w.r.t.评分排序的。
However, only for VMTF, bumped variables are guaranteed to be enqueued at the end (head) of the queue, i.e., in constant time.
译文:但是,只有在VMTF中,保证会在队列的末端(头)排队,即,在常数时间内
For other scoring schemes, a linear search is required to find the right position,
which risks an accumulated quadratic bumping effort.
译文:对于其他的评分方案,需要线性搜索来找到正确的位置,这可能会增加二次碰撞的风险。
To reduce enqueue time, we propose three optimizations and two modifications to the bumping order.
译文:为了减少排队时间,我们提出了三个优化和两个修改的碰撞顺序。
The first optimization is inspired by bucket sort and already gives acceptable bumping times for EVSIDS.
译文:第一个优化是受到桶排序的启发,并且已经为evsid提供了可接受的碰撞时间。
It is motivated by the following observation.译文:它是由下面的观察引起的。
For EVSIDS, rescoring to avoid floating-point overflow of scores and score increment
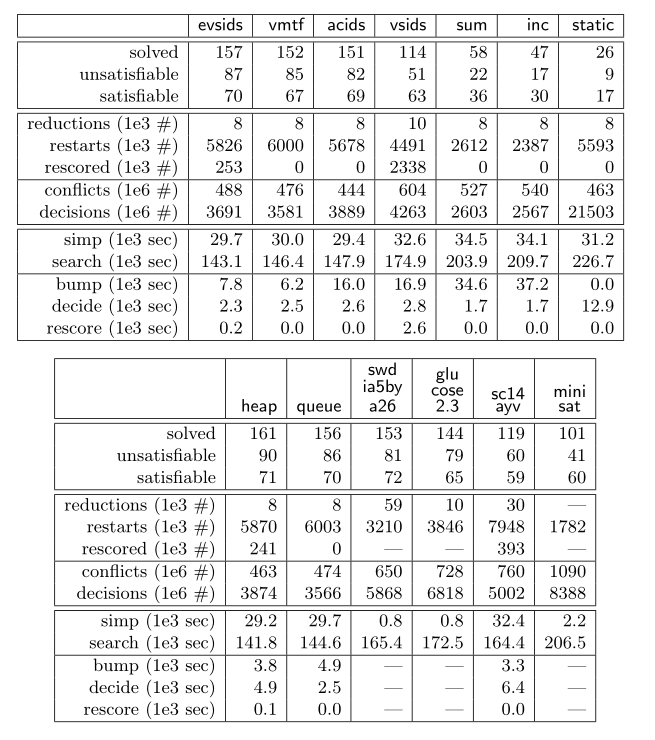
occurs quite frequently, e.g., roughly every 2000 conflicts, as Tab. 2 suggests.
译文:对于evsid,为了避免分数的浮点溢出和分数的增加,重计分的情况经常发生,例如,大约每2000次冲突,如表2所示。
Thus, the exponents of variable scores represented as floating-point numbers
will tend to span the whole range of possible values 3 .
译文:因此,用浮点数表示的变量分数的指数将倾向于跨越可能值的整个范围3。
So instead of a single queue, we keep a stack of queues, indexed by the exponent of the scores of variables.
Variables belong to the queue of the floating-point exponent of their score.
译文:因此,我们不使用单个队列,而是保留一个队列堆栈,根据变量得分的指数进行索引。变量属于其得分的浮点指数的队列。
As the motivation on rescoring shows, this stack will soon grow to its maximum
size for EVSIDS, but for other scoring schemes (particularly for VMTF or INC)
it will only have very few elements or even just one.
译文:正如重新计分的动机所显示的,这个堆栈将很快增长到evsid的最大大小,但对于其他评分方案(特别是VMTF或INC),它将只有很少的元素,甚至只有一个。
------------------------------------------------------------------------------------
Note that, sinceexponents canbenegative, the actual index to access the stack
is obtained after adding the negation of the minimum negative exponent.
译文:注意,因为指数可以是负的,所以访问堆栈的实际索引是在添加最小负指数的否定之后获得的。
Furthermore, Lingeling uses its own implementation of floating-points, in order to
make execution of Lingeling deterministic across different hardware, compilers,
and compiler flags.
译文:而且,为了在不同的硬件、编译器和编译器标记之间确定地执行Lingeling, Lingeling使用自己的浮点数实现。
These software floats have a 32 bit exponent, but we restrict
exponents to 10 bits including a sign bit, by proper rescoring of large scores and
truncation of small scores.
译文:这些软件浮动有一个32位的指数,但我们限制指数为10位,包括一个符号位,通过适当的重取大的分数和截断小的分数。
MiniSAT/Glucose use 10 100 as an upper score limit,
which is only a slightly smaller maximum limit than ours 2 512 ≈ 10 154 , but then
does not use any truncation for small scores, which means that the minimum score
exponent in MiniSAT is (roughly) 2−10 .
MiniSAT/Glucose使用10100作为一个得分上限,这只是一个略小的比我们最大限度2 512≈10154,但是不使用任何截断为小分数,这意味着最低饱和的最低分数指数(大约)2−10。
So Lingeling uses 9 bits for positive scores and 9 bits for negative scores, while MiniSAT uses slightly less than 9 bits for pos-
itives scores and (almost) full 10 bits for negative scores.
译文:因此,Lingeling用9位表示正分数,用9位表示负分数,而minisat用略少于9位表示正分数,用(几乎)10位表示负分数。
When searching for decisions as well as during backtracking, more specifically
during unassigning variables, we additionally have to maintain the highest expo-
nent of an unassigned variable.
译文:当搜索决策以及回溯时,更具体地说,在未分配变量期间,我们还必须维护未分配变量的最高显示值。
This follows the same idea as for next-search in
a single queue and only adds constant time effort for all considered operations.
译文:这与单个队列中的next-search相同,只是为所有考虑的操作增加了常数时间。
During conflict analysis, variables participating in resolutions to derive a learned clause are collected on a seen-variables stack, before they are bumped
(or discarded if on-the-fly subsumption succeeds).
译文:在冲突分析期间,在碰撞之前,将参与生成已学习子句的解决方案的变量收集到一个see-variables堆栈中(如果动态合并成功,则丢弃)。
The analysis traverses the trail of assigned variables in reverse order. Thus, there is a similarity between
the order of variables on the seen-variables stack and the reverse order of assign ments.
译文:分析以相反的顺序遍历指定变量的踪迹。因此,在seen-variables堆栈上的变量顺序与赋值的相反顺序之间存在相似性。
However, this is not guaranteed, particularly for variables with smaller
decision-level. The order of bumping these variables then follows this order too.
译文:然而,这并不能保证,特别是对于决策级别较小的变量。碰撞这些变量的顺序也遵循这个顺序。
At a conflict, it can happen that thousands of variables with different score
are bumped and end up in almost random order w.r.t score order on the seen-
variables stack (or worse, in reverse order) before they are bumped. For many of
these variables, even for EVSIDS, the new updated score might end up having the
same exponent and all those variables have to be enqueued to the same queue.
However, since their scores still differ, enqueueing them degrades to insertion-
sort. There are instances where bumping leads to a time-out due to this effect.
译文:
在冲突中,可能会发生数千个不同分数的变量被碰撞,并以几乎随机的顺序结束。在被碰撞之前,被看见的变量堆栈上的得分顺序(或者更糟,以相反的顺序)。对于这些变量中的许多,甚至对于evsid,新更新的分数最终可能具有相同的指数,所有这些变量都必须加入到相同的队列中。然而,由于他们的分数仍然不同,排队他们退化到插入排序。在某些情况下,碰撞会导致超时。
A first modification to the order in which variables are bumped prevents
this problem. Before actually first dequeuing a bumped variable, then updating its
score,and finally enqueueing it back,we sort the seen-variables stack w.r.t. increas-
ing score. However, a similar problem occurs if all bumped variables have the same
score exponent, which also does not change during update. This is for instance
almost always the case for INC. The second modification prevents this corner
case by first dequeuing all variables on the seen-variables stack, and only then
updating their score and enqueueing them back in score order.
译文:对变量碰撞顺序的第一次修改可以避免这个问题。在实际执行之前,首先将一个已碰撞的变量退出队列,然后更新它的分数,最后再将它重新加入队列,我们对已看到的变量堆栈w.r.t.递增分数进行排序。但是,如果所有的碰撞变量都具有相同的分数指数,则会出现类似的问题,而且在更新期间分数指数也不会改变。以INC为例,几乎总是如此。第二个修改通过首先在seen-variables堆栈上删除所有变量,然后更新它们的分数和enqueu来防止这种情况。
While EVSIDS exponents of variable scores are more or less spread out, other schemes do not have this property, clearly not INC, but probably also SUM and
ACIDS to a smaller extent. For these schemes, score exponents might cluster
around some few values. Thus, our second optimization repeats the bucket
sort argument w.r.t. some fixed number of highest bits of the mantissa of a
variable score. For each queue (indexed by exponent), we add another cache-
table (indexed by highest bits of mantissa) of references pointing to the last
element in the queue with matching highest mantissa bits.
译文:虽然EVSIDS的可变分数指数或多或少是分散的,但其他方案没有这种特性,显然不是INC,但也可能是SUM和ACIDS到一个较小的程度。对于这些方案,分数指数可能会聚集在几个值周围。因此,我们的第二个优化重复bucket sort参数w.r.t.,即变量分数尾数的最高位的固定数目。对于每个队列(按指数索引),我们添加另一个缓存表(按尾数最高位索引)的引用,这些引用指向具有匹配最高尾数位的队列中的最后一个元素。
This ensures that
these variables referenced in the cache-table have the maximum score among
variables in this queue with the same highest bits of the mantissa of their score.
In our implementation, we use the highest 8 bits and thus a cache-table of size
256. This cache is only used for fast enqueue and can be ignored otherwise.
译文:这可以确保在缓存表中引用的这些变量在这个队列中的变量中拥有与其得分尾数相同的最高位的最大得分。在我们的实现中,我们使用最高的8位,因此使用大小的缓存表256. 此缓存仅用于快速入队,否则可以忽略。
If bumping individual variables is done in the order of their scores, as sug-
gested by the first modification above, there is a high chance that consecutively
bumped variables end up in the same queue one after each other or at least close
to each other. Thus, as a third optimization, we propose to additionally cache
the last-enqueued variable for each (sub) queue consisting of variables with the
same highest mantissa bits.
译文:如果像上面第一次修改所建议的那样,按照得分的顺序对单个变量进行碰撞,那么连续碰撞的变量很有可能一个接一个地排在同一个队列中,或者至少接近于这个队列。因此,作为第三个优化,我们建议为每个(子)队列额外缓存last-enqueued变量,该队列由具有相同最高尾数位的变量组成。
In an enqueue operation, we first check whether the
corresponding cache-table entry of the second optimization points to a variable
with smaller (or equal) score. If this is the case, we enqueue right next to it. Oth-
erwise, we obtain the last-enqueued variable and start searching for the proper
enqueue position from there towards the end, e.g., towards larger scores.
译文:在队列操作中,我们首先检查第二个优化的相应缓存表条目是否指向得分较小(或相等)的变量。如果是这样,我们就在它旁边排队。另一方面,我们获得最后排队的变量,并从最后开始搜索合适的排队位置,例如,指向更大的分数。
This might fail if the score of the last-enqueued variable is larger or if the last-enqueue
reference is not valid, e.g., if the variable is already dequeued. We then search
backwards from the cache-table reference (towards smaller scores).
译文:如果last-enqueued变量的得分较大,或者last-enqueue引用无效(例如,如果该变量已经dequeued),则此操作可能失败。然后,我们从缓存表引用向后搜索(指向更小的分数)。
Altogether, these optimizations and modifications seem to avoid the most
severe worst-case corner cases. We track this by profiling relative and total decide
and particularly bump time per instance. Total time summed for these over all
instances are shown in Tab. 2. Further distribution plots are included in the
additional material, mentioned in the results in Sect. 4.
译文:总之,这些优化和修改似乎避免了最严重的最坏情况。我们通过分析相对和总体决定来跟踪它,特别是每个实例的碰撞时间。所有这些实例的总计时间如表2所示。在第4节的结果中提到的其他资料中包括进一步的分布图。
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
3.3 Rescore, Reuse-Trail and Complexity
For the original array based VSIDS implementation, rescoring requires sorting
variables. For a binary heap implementation, one would expect that the heap
does not change, since rescoring does not change the relative order of variables.
However, due to finite precision of scores, even when using floating-points, rescoring will make the score of some variables the same, even though they differed in
score before rescoring.
译文:对于原始的基于数组的VSIDS实现,重新取芯需要排序变量。对于二进制堆实现,应该不会改变堆,因为重新取芯不会改变变量的相对顺序。
然而,由于分数的精度有限,即使使用浮点数,重新取心也会使某些变量的分数相同,即使它们在重新取心之前的分数不同。
Moreover, scores of many variables will become zero after
a few rescores (particularly in EVSIDS). In this situation, the binary heap will
only remain unchanged after rescoring if the actual scores are the only mean to
compare variables (and for instance the variable index is not used as a tie breaker
for comparing variables with the same score). The same argument applies to our
improved queue based implementation.
译文:此外,许多变量的得分在几次重核之后将变为零(特别是在evsid中)。在这种情况下,只有在实际分数是比较变量的唯一方法时,二叉堆才会在重新取心后保持不变(例如,在比较具有相同分数的变量时,不使用变量索引作为决定因素)。同样的理由也适用于我们改进的基于队列的实现。
The reuse-trail optimization [28] is based on the following observation. After
a restart, it often happens that the same decisions are taken and the trail ends
up with the same assigned variables. Thus, the whole restart was useless. By
comparing scores of assigned previous decisions with the score of the next decision variable before restarting, this situation can be avoided.
译文:重用路径优化[28]基于以下观察。在重新启动之后,经常发生的情况是,做出了相同的决定,并以分配相同的变量结束试验。因此,整个重新启动是无用的。通过将分配的前一个决策的得分与重新启动前下一个决策变量的得分进行比较,可以避免这种情况。
With some effort,this technique can be lifted to our generic queue implementation. To simplify
the comparison in favor of a clean experiment, the results presented in Sect 4
are without reuse-trail (except for sc14ayv, the old 2014 version of Lingeling).
译文:通过一些努力,这项技术可以应用到通用队列实现中。为了简化比较以支持干净的实验,第4节中给出的结果没有重复使用痕迹(sc14ayv除外,2014年版本的Lingeling)。
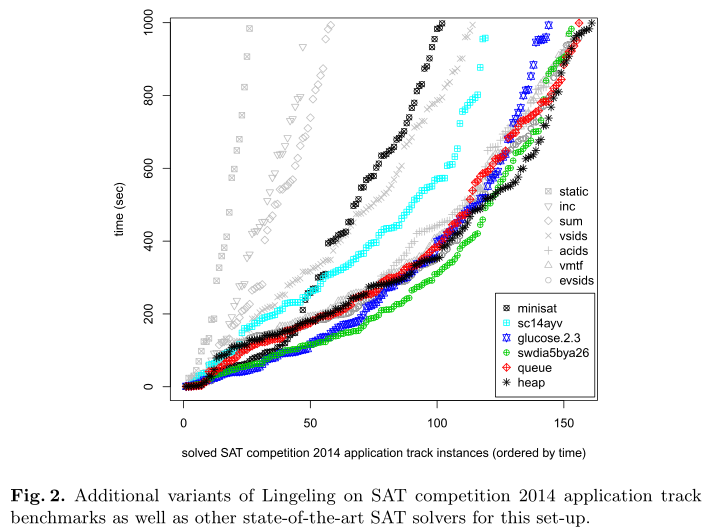
While we do not have a precise complexity analysis for this new data structure, our empirical results show that it performs almost as good as a dedicated
binary heap for EVSIDS (heap) and as a dedicated simplified queue for VMTF (queue).
译文:虽然我们没有对这种新的数据结构进行精确的复杂性分析,但我们的经验结果表明,它的性能几乎与evsid(堆)的专用二进制堆和VMTF(队列)的专用简化队列一样好。
This makes our empirical comparison of decision heuristics more accurate since they all use the same implementation. This data structure should also
allow to experiment with new scoring schemes without the need to implement dedicated data structures.
译文:这使得我们对决策启发法的经验比较更加准确,因为它们都使用相同的实现。这种数据结构还应该允许试验新的评分方案,而不需要实现专用的数据结构。
It might also be possible to improve it further, while our binary heap implementation is close to being as fast and compact as possible.
译文:还可以进一步改进它,同时我们的二进制堆实现也尽可能快和紧凑。