作业三：结对项目

结对项目

一、作业介绍

这个作业属于哪个课程	班级的链接
这个作业要求在哪里	作业要求的链接
这个作业的目标	完成小学四则运算题目的命令行程序，熟悉项目开发流程，提高团队合作能力

二、成员信息

代码仓库	GitHub
成员1	杨智雄-3122004409
成员2	陈愉锋-3122004387

三、效能分析

各模块耗时

使用Python自带的性能分析模块cProfile进行性能分析。由于答案检查功能只用到单个函数make_correction，性能分析意义较小，故仅对题目生成功能进行性能分析。
  在终端中输入对应命令，并以cumtime（指定的函数及其所有子函数从调用到退出消耗的累积时间）降序排序，分别测试在生成100个题目、1000个题目、10000个题目时的程序性能（表达式的数值范围均为[1, 20]），结果如下：
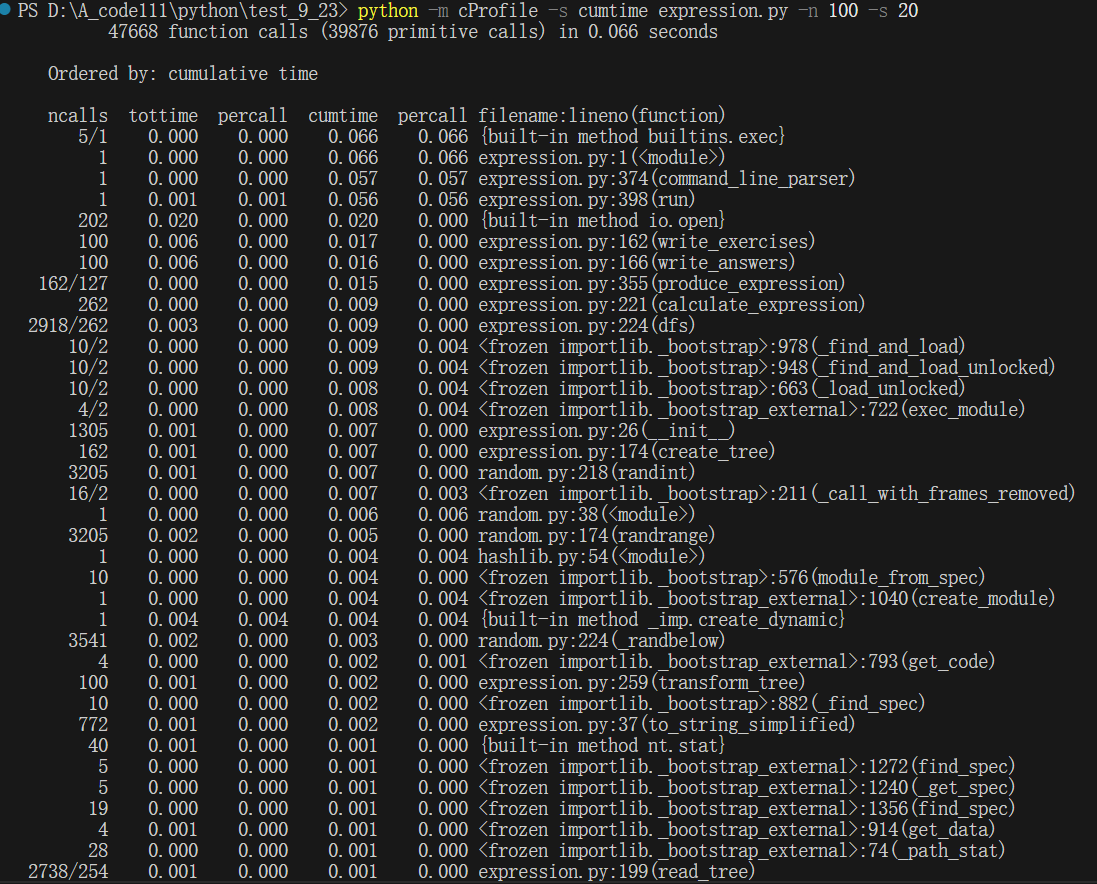
  生成100个题目时：

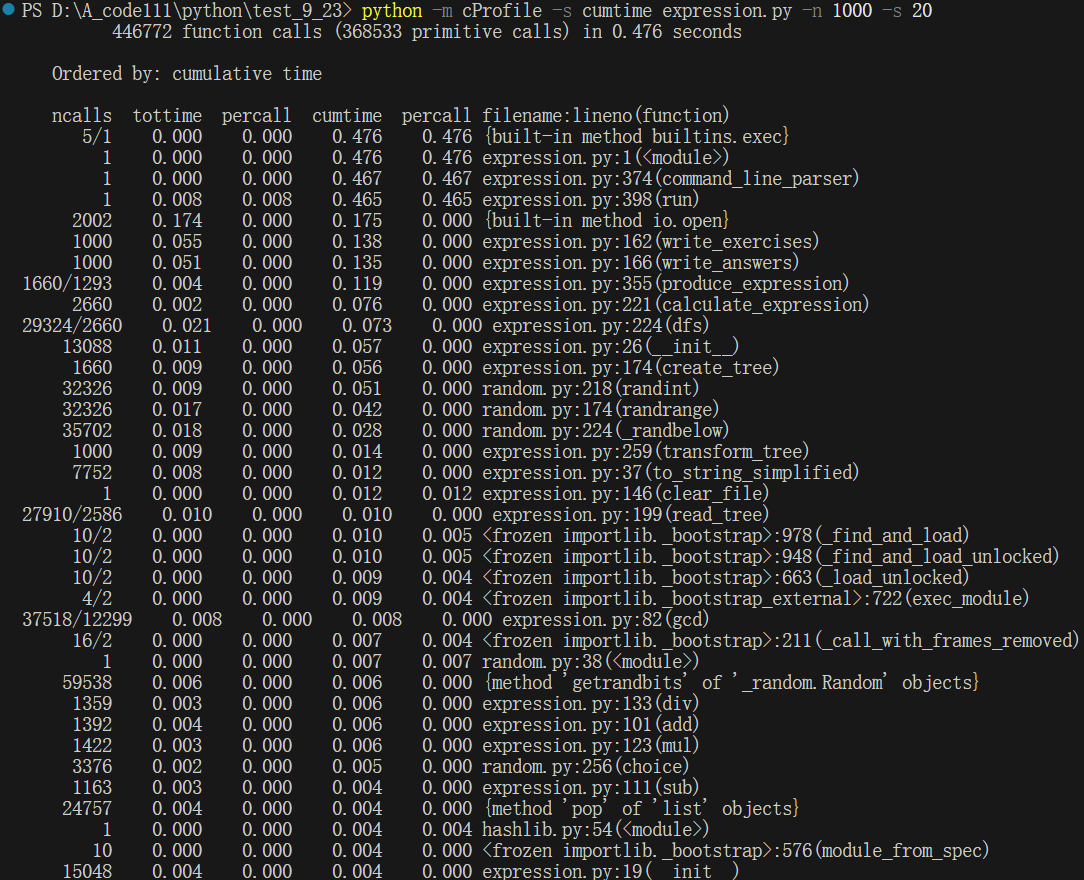
生成1000个题目时：

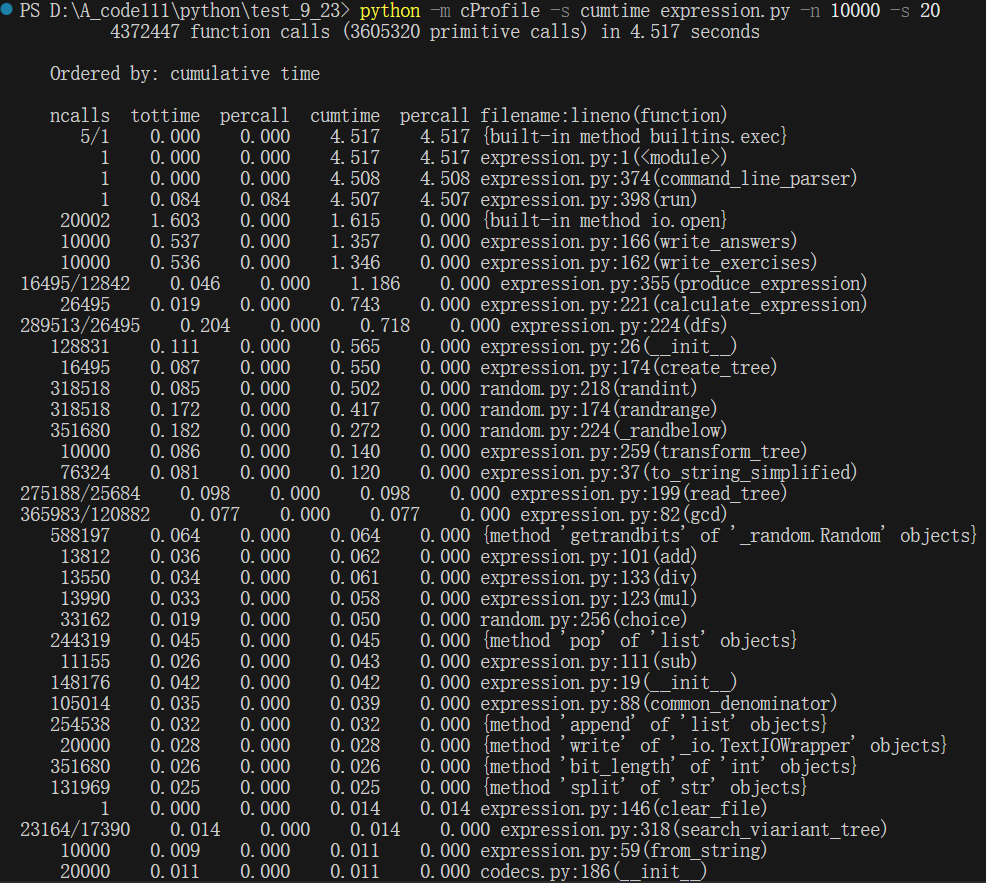
生成10000个题目时：

生成10w个题目时：

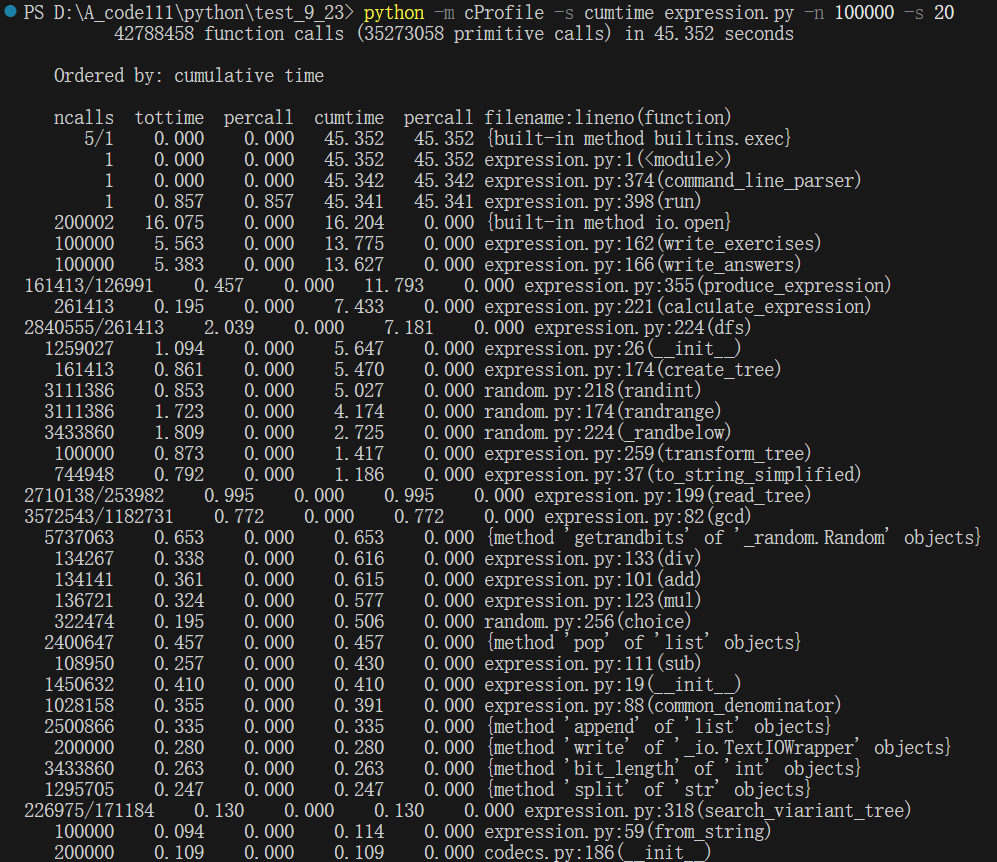
可以看到，在生成100个题目、1000个题目、10000个、10w个题目时，分别耗时0.066s、0.476s、4.517s，45.352s题目生成效率分别为：1515.15题/s、2100.84题/s、2213.86题/s，2204.97题/s,说明生成的题目越多、题目生成的效率越高，不过效率的增加率有略微减缓,这说明代码中的算法已经达到最优，基本呈现O(n)的复杂度，时间消费很低。
  分析函数占用的时间，发现在生成100个题目、1000个题目、10000个题目，10w个题目时，函数produce_tree的耗时占总耗时的比例分别为：22.7%、25%、26.3%，26%可以看到：随着题目生成增多，函数produce_tree的耗时占用比例呈线性，无明显变化。

四、设计与实现

1.二叉树结构

四种树型：

2.代码中各类与函数间关系：

主要类	类中主要函数	作用
main	produce_expression check_answer command_line_parser	负责调用其他模块生成表达式和答案，检查文件的答案，和提供命令面板的参数控制
Fraction	to_string_simplified from_string common_denominator gcd add sub mul div	负责操作数的处理层，包括对操作数初始化，化简，通分，和基本的加减乘除运算
BinaryTree	create_tree read_tree calculate_expression transform_tree search_viariant_tree	负责表达式的处理层，用二叉树存放表达式，实现表达式在字符串类型和二叉树形式之间的转换，后序遍历树得到逆波兰表达式配合栈计算结果，以及在二叉树形式上使用生成器寻找所有变体树实现表达式查重
FileUtil	clear_file clear_grade read_exercises write_exercises read_answers write_answers write_grade	负责文件的操作层，具体实现有输入前清空对应文件、将生成的表达式和计算后的答案写入对应文件、读取题目文件和答案文件存入列表、将正确和错误的题目序号存放在成绩文件中

3.流程图：

4.文件结构及其覆盖率：

5.测试结果：

输入python main.py -n 10000 -s 20生成题目与答案

输入python main.py -e exercises.txt -a answers.txt校对答案

故意改错答案后再次输入python main.py -e exercises.txt -a answers.txt 进行校对

五、代码说明

Main.py

导入argparse

from FileUtil import *
import argparse
random_max=10# 默认值

(函数)通过递归生成表达式 返回值为字符串类型的表达式produce_expression()

def produce_expression():
    init = random.randint(1, 3)
    tree_root = create_tree(init)
    calculate_expression(tree_root)# 这是一步验算
    if tree_root.error==0 and read_tree(tree_root) not in expressions_list:
        viariant_trees=search_viariant_tree(tree_root)
        for viariant_tree in viariant_trees:  # 迭代生成器
            expressions_list.append(read_tree(viariant_tree))  # 处理并添加生成的表达式
        return read_tree(tree_root)
    else:
        produce_expression()

(函数)检查答案正确性check_answer()

def check_answer(expressions_list,answers_list):
    for i in range(len(expressions_list)):
        if answers_list[i] == Fraction().from_string(calculate_expression(transform_tree(expressions_list[i]))).to_string_simplified():
            right_answers_list.append(i+1)
        else:
            wrong_answers_list.append(i+1)

(函数)命令行参数解析command_line_parser()

def command_line_parser():
    global random_max
    parser = argparse.ArgumentParser(description='Fraction arithmetic calculator')
    parser.add_argument('-n', '--number', type=int, default=0, help='number of exercises')
    parser.add_argument('-e','--exercise_path', type=str, default=None, help='exercise file path')
    parser.add_argument('-a','--answer_path', type=str, default=None, help='answer file path')
    parser.add_argument('-s', '--random_max', type=int, default=None, help='random maximum value')
    args = parser.parse_args()
    if args.exercise_path !=  None and args.answer_path != None:
        FileUtil().clear_grade()
        FileUtil().read_exercises()
        FileUtil().read_answers()
        check_answer(exercises_list,answers_list)
        FileUtil().write_grade()
    elif args.exercise_path != None or args.answer_path != None:
        print("exercise_path and answer_path must be both specified or both not specified")
    if args.random_max != None :
        if args.random_max>0:
            random_max = args.random_max-1
        else:
            print("random seed must be a positive integer")
    if args.number>0:
        run(args.number)

(函数)生成表达式和对应答案到对应文件中，接口为int类型的生成表达式条数run(n)

def run(n):
    FileUtil().clear_file()
    while n>0:
        test_str=produce_expression()
        if test_str != None:
            FileUtil().write_exercises(test_str+"=")
            root=transform_tree(test_str)
            result=calculate_expression(root)
            result=Fraction().from_string(result).to_string_simplified()
            FileUtil().write_answers(result)
            n-=1

运行部分

command_line_parser()

BinaryTree.py

初始化列表和运算符字典

from Fraction import *

symbols = ['+', '-', '×', '÷']  # 运算符字典
precedence = {
        '+': 1,
        '-': 1,
        '×': 2,
        '÷': 2
    }# 优先级字典
expressions_list = []  # 表达式列表
exercises_list = []  # 练习题列表
answers_list = []  # 答案列表
right_answers_list = [] # 正确答案序号列表
wrong_answers_list = [] # 错误答案序号列表

(类)节点的格式

class Node:


    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None
        self.error = 0  # 异常标志位：0表示正常，1表示异常 包括负数异常、除数为0异常

(函数)针对四种树型进行随机选择生成 接口为int类型的运算符个数，返回值为节点类型的根节点create_tree(symbols_num)

def create_tree(symbols_num):
    random_one = random.choice(symbols)
    root = Node(random_one)  # 创建新的节点
    root.left = Node(Fraction().to_string_simplified())  # 递归创建左子树
    root.right = Node(Fraction().to_string_simplified())  # 递归创建右子树
    if symbols_num > 1:
        random_two = random.choice(symbols)
        root2 = Node(random_two)  # 创建新的节点
        root.left = root2  # 递归创建左子树
        root2.left = Node(Fraction().to_string_simplified())  # 递归创建左子树
        root2.right = Node(Fraction().to_string_simplified())  # 递归创建右子树
    if symbols_num > 2:
        random_three = random.choice(symbols)
        root3 = Node(random_three)  # 创建新的节点
        choice = random.randint(1, 2)
        if choice == 1:
            root2.left = root3  # 递归创建左子树
            root3.left = Node(Fraction().to_string_simplified())  # 递归创建左子树
            root3.right = Node(Fraction().to_string_simplified())  # 递归创建右子树
        if choice == 2:
            root.right = root3  # 递归创建右子树
            root3.left = Node(Fraction().to_string_simplified())  # 递归创建左子树
            root3.right = Node(Fraction().to_string_simplified())  # 递归创建右子树
    return root  # 返回根节点

(函数)中序遍历树实现读取表达式 返回值为字符串类型的表达式 def read_tree(node)

def read_tree(node):
    str = ""
    if node is None:
        return str  # 如果节点为空，则返回
    if node.left is not None and node.left.value in ['+', '-'] and node.value in ['×', '÷']:
        str += "("
        str += read_tree(node.left)
        str += ")"
    else:
        str += read_tree(node.left)

    str += node.value

    if node.right is not None and node.right.value in ['+', '-'] and node.value in ['×', '÷']:
        str += "("
        str += read_tree(node.left)
        str += ")"
    else:
        str += read_tree(node.right)

    return str

(函数)利用后序遍历树和栈结构计算表达式的值 返回值为字符串类型的结果calculate_expression(tree_root)

def calculate_expression(tree_root):
    # 栈压入的是字符串
    stack = []

    def dfs(node):
        if node is None:
            return
        dfs(node.left)
        dfs(node.right)
        stack.append(node.value)
        if stack[-1] == '+':
            stack.pop()
            str = Fraction().add(stack.pop(), stack.pop())
            stack.append(str)
        if stack[-1] == '-':
            stack.pop()
            str = Fraction().sub(stack.pop(), stack.pop())
            if 'fail' in str:
                tree_root.error = 1
                stack.append("-1")
                # print("出现了负数异常 ")
                return
            stack.append(str)
        if stack[-1] == '×':
            stack.pop()
            str = Fraction().mul(stack.pop(), stack.pop())
            stack.append(str)
        if stack[-1] == '÷':
            stack.pop()
            str = Fraction().div(stack.pop(), stack.pop())
            if 'fail' in str:
                tree_root.error = 1
                stack.append("-1")
                # print("出现了除数为0异常")
                return
            stack.append(str)

    dfs(tree_root)
    return stack.pop()

(函数)把表达式转化为树,接口为字符串类型的表达式，返回值为树的根节点transform_tree(expression)

def transform_tree(expression):
    # 去除等于号字符
    expression = expression.replace("=", "")
    optr_stack = []  # 运算符栈
    expt_stack = []  # 表达式树的根节点栈
    current_number = ''
    for char in expression:
        if char.isdigit() or char == '\'' or char == '/':  # 处理数字或分数
            current_number += char
        else:
            if current_number:
                expt_stack.append(Node(current_number))  # 创建数字节点并入栈
                current_number = ''

            if char in symbols:  # 如果是运算符
                while (optr_stack and optr_stack[-1] != '(' and
                       precedence[char] <= precedence[optr_stack[-1]]):
                    # 弹出运算符，构造树
                    top_op = optr_stack.pop()
                    right_node = expt_stack.pop()
                    left_node = expt_stack.pop()
                    operator_node = Node(top_op)
                    operator_node.left = left_node
                    operator_node.right = right_node
                    expt_stack.append(operator_node)  # 重新将构造的树根节点压入expt栈

                optr_stack.append(char)  # 将当前运算符压入运算符栈

            elif char == '(':
                optr_stack.append(char)  # 左括号直接入运算符栈

            elif char == ')':
                while optr_stack and optr_stack[-1] != '(':
                    # 弹出运算符，构造树
                    top_op = optr_stack.pop()
                    right_node = expt_stack.pop()
                    left_node = expt_stack.pop()
                    operator_node = Node(top_op)
                    operator_node.left = left_node
                    operator_node.right = right_node
                    expt_stack.append(operator_node)  # 重新将构造的树根节点压入expt栈

                optr_stack.pop()  # 弹出左括号

    if current_number:  # 处理最后一个数字
        expt_stack.append(Node(current_number))

    # 处理栈中剩余的内容
    while optr_stack:
        top_op = optr_stack.pop()
        right_node = expt_stack.pop()
        left_node = expt_stack.pop()
        operator_node = Node(top_op)
        operator_node.left = left_node
        operator_node.right = right_node
        expt_stack.append(operator_node)  # 将新形成的子树放回栈

    return expt_stack[0] if expt_stack else None  # 返回根节点

(函数)把根节点对应的树进行变换 把树中所有加号和乘号的左右子树交换的情况 返回值为所有变体树的根节点生成器 比如(1+2)×3有3种变体(2+1)*3,3*(1+2),3*(2+1),在表达式形式上都是顺序问题，实现了O(n)的实现复杂度search_viariant_tree(node)

def search_variant_tree(node):
    if node is None:
        return []

    # 递归处理左子树和右子树
    left_trees = search_variant_tree(node.left)
    right_trees = search_variant_tree(node.right)

    variants = []

    # 处理加法和乘法节点
    if node.value in ['+', '×']:
        # 生成左右组合
        for left_tree in left_trees:
            for right_tree in right_trees:
                new_tree1 = Node(node.value)
                new_tree1.left = left_tree
                new_tree1.right = right_tree
                variants.append(new_tree1)

                new_tree2 = Node(node.value)
                new_tree2.left = right_tree
                new_tree2.right = left_tree
                variants.append(new_tree2)
    else:
        # 对其他运算符处理
        for left_tree in left_trees:
            new_tree = Node(node.value)
            new_tree.left = left_tree
            new_tree.right = node.right
            variants.append(new_tree)

        for right_tree in right_trees:
            new_tree = Node(node.value)
            new_tree.left = node.left
            new_tree.right = right_tree
            variants.append(new_tree)
    
    # 当没有子树时，返回当前节点作为变体
    if not variants:
        variants.append(node)

    return variants

FileUtil.py

(类)包含五种文件读写函数和一种清空文件函数 主要负责文件的处理层

导入二叉树类的函数

from BinaryTree import *

(函数)清空题目文件和答案文件clear_file(self)

def clear_file(self):
        with open("exercises.txt", 'r+') as file:
            file.truncate(0)
        with open("answers.txt", 'r+') as file:
            file.truncate(0)

(函数)清空成绩文件clear_grade(self)

def clear_grade(self):
        with open("grade.txt", 'r+') as file:
            file.truncate(0)

(函数)读取题目文件read_exercises(self)

def read_exercises(self):
        with open('exercises.txt', 'r', encoding="utf-8") as f:
            for line in f:
                exercises_list.append(line.strip().replace("=", ""))

(函数)读取答案文件read_answers(self)

def read_answers(self):
        with open('answers.txt', 'r', encoding="utf-8") as f:
            for line in f:
                answers_list.append(line.strip())

(函数)写入题目文件write_exercises(self, str)

def write_exercises(self, str):
        with open('exercises.txt', 'a', encoding="utf-8") as f:
            f.write(str + "\n")

(函数)写入答案文件write_answers(self, str)

def write_answers(self, str):
        with open('answers.txt', 'a', encoding="utf-8") as f:
            f.write(str + "\n")

(函数)写入成绩文件write_grade(self)

def write_grade(self):
        with open('grade.txt', 'a', encoding="utf-8") as f:
            f.write(
                f"Right:{len(right_answers_list)}{right_answers_list}\nWrong:{len(wrong_answers_list)}{wrong_answers_list}\n")

Fraction.py

（类）包含各种数据的格式转换函数 还有数据的随机生成和运算功能 主要负责对分数的格式、生成、运算

导入random库

import random
random_max=10# 默认值

(函数)初始化操作数，以70%的概率生成整数，__init__(self)

def __init__(self):
        cinque = random.randint(1, 10)  # 摇骰子1点到10点
        if cinque <= 7:
            self.numerator = random.randint(1, random_max)
            self.denominator = 1
            self.interger = 0
        else:
            self.numerator = random.randint(1, random_max)
            self.denominator = random.randint(1, random_max)
            self.integer = 0

(函数)把操作数化简，返回值为字符串类型的结果 to_string_simplified(self)

def to_string_simplified(self):
        if self.numerator // self.denominator > 0 and self.numerator % self.denominator != 0:
            integer = self.numerator // self.denominator
            numerator = self.numerator % self.denominator
            gcd1 = Fraction.gcd(numerator, self.denominator)
            numerator = numerator // gcd1
            self.denominator = self.denominator // gcd1
            if self.denominator == 1:
                return f"{integer}\'{numerator}"
            return f"{integer}\'{numerator}/{self.denominator}"
        if self.numerator == self.denominator:
            self.integer = 1
            self.numerator = 0
            self.denominator = 1
            return f"{1}"
        gcd1 = Fraction.gcd(self.numerator, self.denominator)
        self.numerator = self.numerator // gcd1
        self.denominator = self.denominator // gcd1
        if self.denominator == 1:
            return f"{self.numerator}"
        return f"{self.numerator}/{self.denominator}"

(函数)接口是字符串类型的操作数，返回值是赋初始值为操作数相应属性的对象from_string(self, Fraction_str)

def from_string(self, Fraction_str):
        self.integer = 0
        if "\'" in Fraction_str:
            integer_part, Fractional_part = Fraction_str.split("\'")
            self.integer = int(integer_part)
            numerator, denominator = Fractional_part.split("/")
            self.denominator = int(denominator)
            self.numerator = self.integer * self.denominator + int(numerator)

        # 处理普通分数
        elif "/" in Fraction_str:
            numerator, denominator = Fraction_str.split("/")
            self.denominator = int(denominator)
            self.numerator = int(numerator)

        # 处理整数
        else:
            self.integer = int(Fraction_str)
            self.numerator = 0
            self.denominator = 1
        return self

(函数)辗转相除法求最大公约数gcd(a, b)

def gcd(a, b):
        if b == 0:
            return a
        else:
            return Fraction.gcd(b, a % b)

(函数)将分数通分，接口为字符串类型的操作数，返回值相同类型的操作数common_denominator(self, fraction_str)

def common_denominator(self, fraction_str):
        if '\'' in fraction_str:
            integer_part, Fractional_part = fraction_str.split("\'")
            integer_part = int(integer_part)
            numerator, denominator = Fractional_part.split("/")
            denominator = int(denominator)
            numerator = integer_part * denominator + int(numerator)
            return f"{numerator}/{denominator}"
        if '/' not in fraction_str:
            return f"{fraction_str}/1"
        else:
            return fraction_str

(函数)加法add()

def add(self, fraction_a, fraction_b):
        fraction_a = self.common_denominator(fraction_a)
        fraction_b = self.common_denominator(fraction_b)
        numerator_a, denominator_a = fraction_a.split("/")
        numerator_b, denominator_b = fraction_b.split("/")
        numerator = int(numerator_a) * int(denominator_b) + int(numerator_b) * int(denominator_a)
        denominator = int(denominator_a) * int(denominator_b)
        gcd = Fraction.gcd(numerator, denominator)
        return f"{numerator // gcd}/{denominator // gcd}"

(函数)减法sub()

def sub(self, fraction_b, fraction_a):
        fraction_a = self.common_denominator(fraction_a)
        fraction_b = self.common_denominator(fraction_b)
        numerator_a, denominator_a = fraction_a.split("/")
        numerator_b, denominator_b = fraction_b.split("/")
        numerator = int(numerator_a) * int(denominator_b) - int(numerator_b) * int(denominator_a)
        if numerator < 0:
            return "fail"
        denominator = int(denominator_a) * int(denominator_b)
        gcd = Fraction.gcd(numerator, denominator)
        return f"{numerator // gcd}/{denominator // gcd}"

(函数)乘法mul()

def mul(self, fraction_a, fraction_b):
        fraction_a = self.common_denominator(fraction_a)
        fraction_b = self.common_denominator(fraction_b)
        numerator_a, denominator_a = fraction_a.split("/")
        numerator_b, denominator_b = fraction_b.split("/")
        numerator = int(numerator_a) * int(numerator_b)
        denominator = int(denominator_a) * int(denominator_b)
        gcd = Fraction.gcd(numerator, denominator)
        return f"{numerator // gcd}/{denominator // gcd}"

(函数)除法div()

def div(self, fraction_b, fraction_a):
        fraction_a = self.common_denominator(fraction_a)
        fraction_b = self.common_denominator(fraction_b)
        numerator_a, denominator_a = fraction_a.split("/")
        numerator_b, denominator_b = fraction_b.split("/")
        if int(numerator_b) == 0:
            return "fail"
        numerator = int(numerator_a) * int(denominator_b)
        denominator = int(numerator_b) * int(denominator_a)
        gcd = Fraction.gcd(numerator, denominator)
        return f"{numerator // gcd}/{denominator // gcd}"

六、测试运行

针对4类不同函数的10项测试：

Test.py

1.测试分数的加减乘除和化简

test_fraction_operations(self)

def test_fraction_operations(self):
        a = Fraction().from_string("2/3")  # 2/3的字符串表示
        b = Fraction().from_string("1/3")  # 1/3的字符串表示
        a_str = a.to_string_simplified()
        b_str = b.to_string_simplified()

        # 测试加法
        add_result = Fraction().add(a_str, b_str)
        expected_add = "1/1" 
        self.assertEqual(add_result, expected_add, f"加法结果错误: {a_str} + {b_str} = {add_result}")

        # 测试减法
        sub_result = Fraction().sub(b_str, a_str)
        expected_sub = "1/3" 
        self.assertEqual(sub_result, expected_sub, f"减法结果错误: {a_str} - {b_str} = {sub_result}")

        # 测试乘法
        mul_result = Fraction().mul(a_str, b_str)
        expected_mul = "2/9"
        self.assertEqual(mul_result, expected_mul, f"乘法结果错误: {a_str} * {b_str} = {mul_result}")

        # 测试除法
        if int(b.numerator) != 0:  # 确保不除以零
            div_result = Fraction().div(b_str, a_str)
            expected_div = "2/1"
            self.assertEqual(div_result, expected_div, f"除法结果错误: {a_str} / {b_str} = {div_result}")
        else:
            self.assertEqual(Fraction().div(a_str, b_str), "fail", f"如果除数为零，应返回 'fail'")

2.测试最大公约数

test_gcd(self)

def test_gcd(self):
        self.assertEqual(Fraction.gcd(10, 5), 5, "gcd 方法错误")
        self.assertEqual(Fraction.gcd(17, 5), 1, "gcd 方法错误")

3.测试化简

test_to_string_simplified(self)

def test_to_string_simplified(self):
        # 测试分数转字符串的功能
        fraction = Fraction()
        fraction.numerator = 5
        fraction.denominator = 10
        self.assertEqual(fraction.to_string_simplified(), "1/2", "to_string_simplified 方法错误")

        fraction.numerator = 7
        fraction.denominator = 1
        self.assertEqual(fraction.to_string_simplified(), "7", "to_string_simplified 方法错误")

        fraction.numerator = 0
        fraction.denominator = 1
        self.assertEqual(fraction.to_string_simplified(), "0", "to_string_simplified 方法错误")

        fraction.numerator = 8
        fraction.denominator = 7
        self.assertEqual(fraction.to_string_simplified(), "1'1/7", "to_string_simplified 方法错误")

4.测试字符串转对象

test_from_string(self)

def test_from_string(self):
        fraction = Fraction()
        fraction.from_string("2'3/4")
        self.assertEqual(fraction.numerator, 11)
        self.assertEqual(fraction.denominator, 4, "from_string 方法错误")

        fraction.from_string("3/5")
        self.assertEqual(fraction.numerator, 3)
        self.assertEqual(fraction.denominator, 5, "from_string 方法错误")

        fraction.from_string("6")
        self.assertEqual(fraction.numerator, 0)
        self.assertEqual(fraction.denominator, 1, "from_string 方法错误")

5.测试表达式转换和计算

test_transform_tree_and_calculate(self)

def test_transform_tree_and_calculate(self):
        a = Fraction().from_string("1/3")
        b = Fraction().from_string("1/2")
        expression = f"{a.to_string_simplified()}+{b.to_string_simplified()}"
        tree_root = transform_tree(expression)
        result = calculate_expression(tree_root)
        result_str = Fraction().from_string(result).to_string_simplified()

        # 计算预期结果
        expected_result = Fraction().add(a.to_string_simplified(), b.to_string_simplified())
        self.assertEqual(result_str, expected_result)

6.测试树结构读取为表达式字符串

test_read_tree(self)

def test_read_tree(self):
        for _ in range(10):
            a = Fraction()
            b = Fraction()
            expression = f"{a.to_string_simplified()}+{b.to_string_simplified()}"
            tree_root = transform_tree(expression)
            read_expr = read_tree(tree_root)
            self.assertEqual(read_expr, expression)

7.（关键测试）查重算法测试 证明了查重算法的有效

test_from_string(self)

def test_search_variant_tree_strict(self):
        # 构建树: (1 + 2) × 3
        root = Node('×')
        root.left = Node('+')
        root.left.left = Node('1')
        root.left.right = Node('2')
        root.right = Node('3')

        # 生成所有变体
        variants = search_variant_tree(root)

        # 打印生成的变体
        generated_expressions = [read_tree(variant) for variant in variants]
        print(f"Generated Variants: {generated_expressions}")

        # 生成预期的变体
        expected_variants = [
            '(1+2)×3',
            '(2+1)×3',
            '3×(1+2)',
            '3×(2+1)'
        ]

        # 确保每个预期变体都可以被确认
        for expected in expected_variants:
            self.assertIn(expected, generated_expressions, f"未检测到变体: {expected}")

        print("所有变体均已检测到!")

8.测试运算表达式

test_calculate_expression(self)

def test_calculate_expression(self):
        root = Node('+')
        root.left = Node('1')
        root.right = Node('1/2')
        self.assertEqual(calculate_expression(root), '3/2', "计算表达式值错误")

9.测试表达式转换为树

test_transform_tree(self)

def test_transform_tree(self):
        expression = "1/2 + 1/2"
        tree_root = transform_tree(expression)
        self.assertIsNotNone(tree_root, "转换表达式为树失败，树根节点为None")

10.测试文件操作

test_file_util(self)

def test_file_util(self):
        file_util = FileUtil()
        file_util.clear_file()  # 清空文件
        test_exercise = "3/4+1/2"
        test_answer = "5/4"
        file_util.write_exercises(test_exercise)
        file_util.write_answers(test_answer)

        file_util.read_exercises()
        file_util.read_answers()

        exercises = exercises_list
        answers = answers_list

        self.assertEqual(exercises[0], test_exercise.strip())
        self.assertEqual(answers[0], test_answer.strip())

运行之后得到结果：十项针对不同的函数接口的测试全部通过，从而证明程序的正确性。

七、PSP表格

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planing	计划	40	30
.Estimate	.估计这个任务需要多久时间	30	30
Development	开发	110	150
.Analysis	.需求分析 (包括学习新技术)	30	35
.Design Spec	.生成设计文档	30	35
.Design Review	.设计复审	30	45
.Coding Standrd	.代码规范（为目前的开发制定合适的规范）	15	25
.Design	.具体设计	40	50
.Coding	.具体编码	350	420
.Code Review	.代码复审	20	15
.Test	.测试（自我测试，修改代码，提交修改）	60	70
.Reporting	报告	80	75
.Test Report	.测试报告	30	30
.Size Measurement	.计算工作量	30	20
.Postmortem&Process Improvement	.事后总结，并提出过程改进计划	30	35
	.合计	885	1000

八、项目小结

杨智雄：在项目刚开始选择使用不熟悉的python实现项目，是因为上次个人项目里面python自带库使用很便利，没想到在这次项目中没有发挥它的优势，还吃了不熟悉它的苦头，还好这次项目任务难度可以接受，学习到了挺多的知识，也对面向对象的理解更加深刻。在项目构想初期本来是计划将二人把实现过程规划好后划分功能然后分工实现，然后因为对语言不熟悉，也是第一次团队合作致使计划没能顺利发展，陈愉锋是优秀的合作伙伴，他是我的领航员，在完成代码工作中在测试部分很出色，期待下次可以更好的合作，学会在团队实现项目。

陈愉锋：在刚接触项目时我有点迷茫，在查阅资料与搭档的交流后，我逐渐理解了项目的大致思路，完成项目后我对于后缀表达式与树的理解变得更加深刻。这次的结对项目主要都是杨智雄操刀，他是一个优秀的搭档，有了他的帮助，我才得以完成这个任务，同时他也教了我很多新的知识。