#1037 : 数字三角形
- 例子输入
-
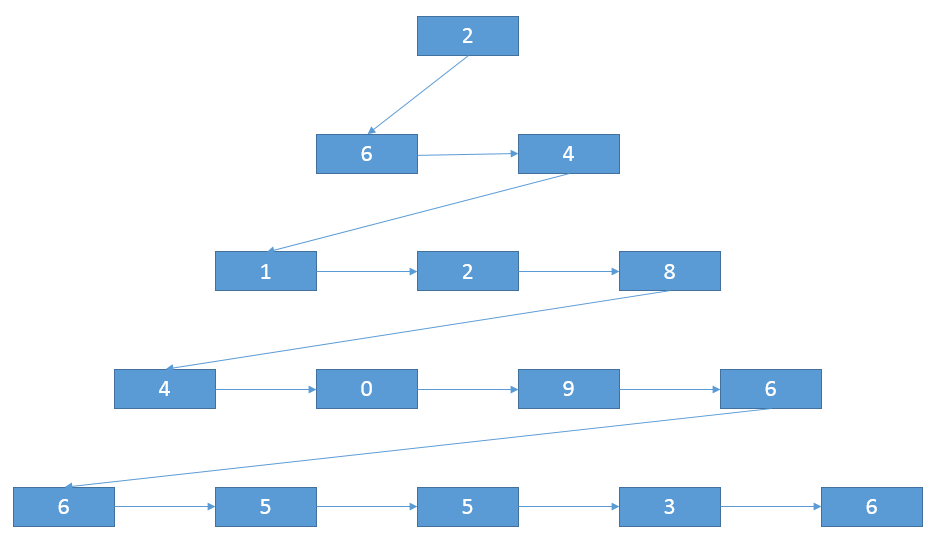
5 2 6 4 1 2 8 4 0 9 6 6 5 5 3 6
- 例子输出
-
28
-
AC代码:
-
#include<bits/stdc++.h> using namespace std; int dp[1010][1010]; int main() { int t,maxx=0; scanf("%d",&t); for(int i=1; i<=t; i++) { for(int j=1; j<=i; j++) { scanf("%d",&dp[i][j]); dp[i][j]+=max(dp[i-1][j],dp[i-1][j-1]); maxx=max(maxx,dp[i][j]); } } printf("%d\n",maxx); }
问题描写叙述
小Hi和小Ho在经历了螃蟹先生的任务之后被奖励了一次出国旅游的机会,于是他们来到了大洋彼岸的美国。
美国人民的生活很有意思,常常会有形形色色、奇奇怪怪的活动举办,这不。小Hi和小Ho刚刚下飞机,就赶上了当地的迷宫节活动。迷宫节里展览出来的迷宫都特别的有意思,可是小Ho却相中了一个事实上并不怎么像迷宫的迷宫——由于这个迷宫的奖励很丰富~
于是小Ho找到了小Hi,让小Hi帮助他获取尽可能多的奖品。小Hi把手一伸道:“迷宫的介绍拿来。”
小Ho选择的迷宫是一个被称为“数字三角形”的n(n不超过200)层迷宫。这个迷宫的第i层有i个房间。分别编号为1..i。除去最后一层的房间。每一个房间都会有一些通往下一层的房间的楼梯,用符号来表示的话,就是从第i层的编号为j的房间出发会有两条路,一条通向第i+1层的编号为j的房间。还有一条会通向第i+1层的编号为j+1的房间。而最后一层的全部房间都仅仅有一条离开迷宫的道路。这种道路都是单向的,也就是说当沿着这些道路前往下一层的房间或者离开迷宫之后。小Ho没有办法再次回到这个房间。迷宫里同一时候仅仅会有一个參与者,而在每一个參与者进入这个迷宫的时候。每一个房间里都会生成一定数量的奖券。这些奖券能够在通过迷宫之后兑换各种奖品。小Ho的起点在第1层的编号为1的房间,如今小Ho悄悄向其它參与者弄清楚了每一个房间里的奖券数量。希望小Hi帮他计算出他最多能获得多少奖券。
提示一:盲目贪心不可取,搜索计算太耗时
小Hi拿到迷宫的介绍。细致想了想,问道:“你自己有什么思路么?”
小Ho想了想,道:“反正每次仅仅有两种选择。我就选通向有很多其它奖券的房间的那条路呗~”
小Hi笑了笑:“你这叫盲目贪心。假设我是迷宫的创造者,一定在第2层的第1个房间放10张奖券。第2个房间一张不放,然后在第3层的第3个房间放999张奖券,这样你就由于占一点小廉价就失掉了大头,你说是不是?”
小Ho一惊:“似乎是的!切记不可因小失大,那……既然我们都是学计算机的学生,不如我们用计算机枚举一下全部可能的路径,然后找到最优的那一条?”
小Hi点了点头:“自然是要用计算机来解决问题,只是你得先计算一下总共同拥有多少条可能的路径。估算一下执行时间。这样才干确定能不能在迷宫节结束之前计算完是不是~”
“我来算算,从出发点開始。每次我都有两种选择。而我总共要做n-1次选择。也就是2的n-1次方,而n最大可能是200,也就是说有2^199条路径……哪怕每条路径我仅仅用一次运算就能够算出它的奖券总数,我毕业之前都肯定算不出来了吧QAQ”小Ho得出了一个很忧伤的结论。
“是的,可是这样的搜索的方法事实上是能够有方法进行优化的哦~”小Hi循循诱导着。
“什么样的方法?”
“别急,听我慢慢说~”
提示二:记忆深搜逞神威,宽度优先解难题
“我们能够来分分情况,我们要搜索全部的路径,然后依次计算每条路径的收益。这是我们如今的问题模型是不是?”小Hi问道。
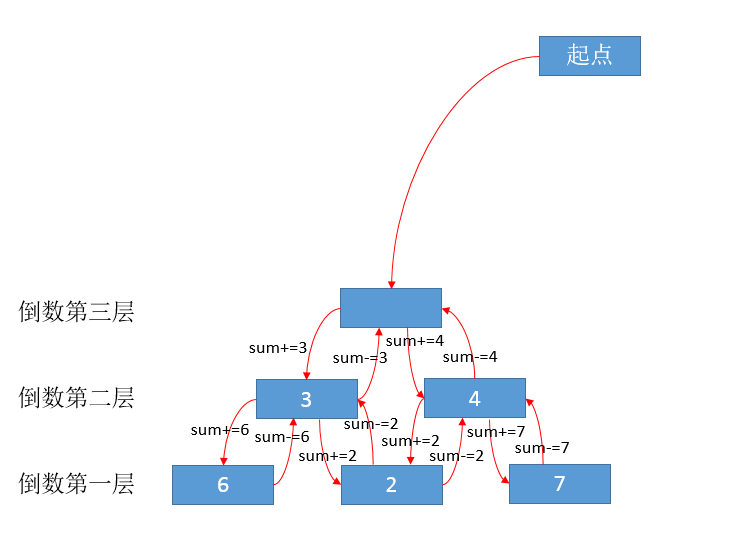
小Ho点头:“细致分析这个迷宫的话,我们有两种搜索方法。一种是深度优先搜索,就像这幅图画的一样。我们先试着顺着每一个房间的第一条路一直下去,一直走到最后一层,然后返回至倒数第二层,选择第二条路走到最后一个房间,然后返回到倒数第三层,选择第二条路走到倒数第二层,然后选择第一条路走到最后一层……期间维护已经走过的房间的奖券之和sum。然后每次到达最后一层的房间的时候将sum与全局最优解ans进行比較,假设sum>ans的话就用sum替换ans。
这样在全部路径都计算过一遍之后,Ans中存储的就是我们要的答案了~~而另外一种……”
“先别说另外一种,我们来看看这样的方法有什么办法优化么~”小Hi打断了小Ho的喋喋不休。
“哦,可是该怎么优化呢?”小Ho问道。
“老规矩,我们来看看这个过程中有什么冗余计算~”小Hi还是那一套说辞,也不操心小Ho听了这么多遍听厌:“看这张图,当你枚举到绿色的‘-》右-》左’这样一条路径的时候,是不是发现它和红色的‘-》左-》右’这条路径一样都到达了第三层的第二个房间?”
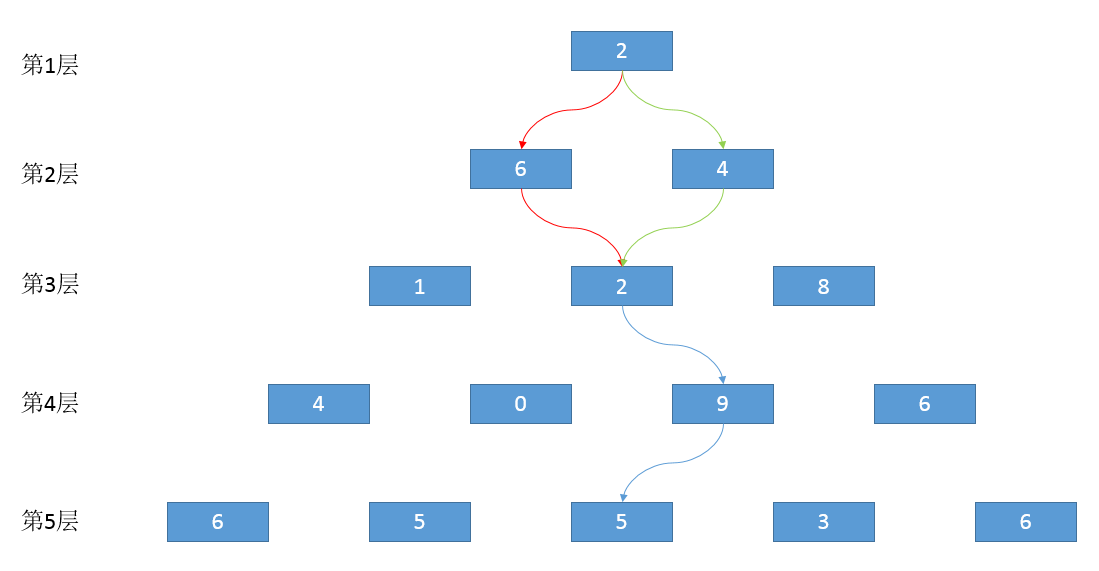
“是的!
”
“在你枚举到绿色路径的时候。是不是红色路径已经被枚举过了?”小Hi接着问道。
“没错!“
“那么你看,绿色路径的奖券和是8,红色路径的奖券和是10,而你们都处于了同样的结点——第3层的第2个房间上,这时候不管你绿色路径接下来延续出什么样的路径。我将从第3层第2个房间開始的这一段连在红色路径之后的话。奖券和都会要比绿色路径要多?”小Hi继续问。
“嗯……对的~”
“而这些路径中的最优值都肯定不超过Ans,不然Ans就会在当时变得和它们一样,这不就说明了绿色路径不管接下来怎样走,都不可能对Ans造成不论什么变化,那我们是不是全然能够不进行接下来的计算了呢?”小Hi做出了最后的结论。
“是的……为了进行这种优化,我们须要记录一个值best(i, j)——当前搜索过的路径中到达第i层第j个房间时最多能获取多少奖券。然后在每次进入一个房间的时候,都检查当前的sum与best(i, j)的大小关系。假设sum小于等于best(i, j)的话。就没有必要继续搜索了呢。
比方在之前的样例中。当通过绿色路径到达第3层第2个房间的时候,best(i, j)=10,而sum = 8,所以是没有必要继续往下搜索的。
”聪明的小Ho非常快就将这个算法总结了出来。
“而这样的做法。因为是通过之前的记忆来避免不必要的搜索。所以被大家称为‘记忆化搜索’”小Ho笑道:“这样,仅仅要不是那种很坏的卡你的情况——比方第i层第j个房间的奖券数是j这样的,都可以在O(n^2)的复杂度通过了呢。
”
“而假设我先右再左呢?”小Ho不死心。
“那我就第i层第j个房间的奖券数是i-j”小Ho邪恶的笑着:“事实上你不用纠结这个。你仅仅要随机一下就行保证差点儿全部情况都是O(n^2)的时间复杂度,或者说平均复杂度是O(n^2),可是你的最坏情况复杂度肯定是降不下去的。所以还是老老实实想想别的方法吧~比方之前你想说的另外一种方法?”
“与深度优先搜索相相应的自然就是宽度优先遍历啦~假设我们用<i, j, k>表示到达第i行的第j个房间,当前获得的奖券数为k这样一个状态,rewards(i, j)表示第i层第j个房间中的奖券数,那么遍历方式就是利用一个队列,先将ə, 1, rewards(1, 1)>这个状态放入队列中。
然后每次取出队首<i, j, k>。假设i==n,就用k更新Ans。不然就将它代表的房间所能到达的两个房间的状态<i + 1, j, k + rewards(i + 1, j)>和<i + 1, j + 1, k + rewards(i + 1, j + 1)>放入队尾。直到整个队列清空,这时候Ans就是我们要的答案。”小Ho缓缓道来。
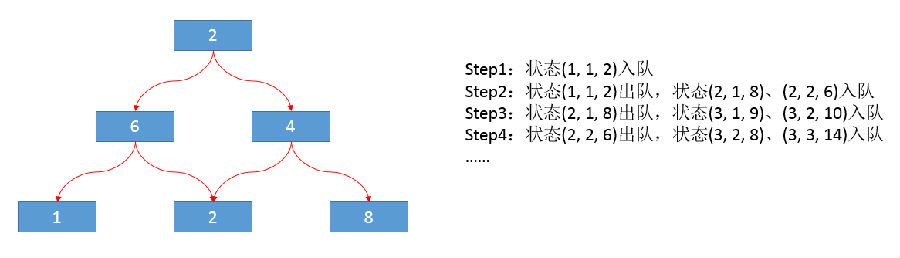
“那你认为这个地方又有什么能够优化的呢?”
“本来我还没想到,可是你说了之前深度优先搜索的问题之后我就有点思路了,你看状态(2, 1, 8)和状态(2, 2, 6)在处理时一个会拓展出(3, 2, 10)这个状态,而还有一个会拓展出(3, 2, 8)这个状态,可是就像我们之前的分析那样(3, 2, 8)这个状态是没有什么用的,它之后不管怎么走。换成(3, 2, 10)按它一样的走法肯定获得的奖券数要很多其它。
”小Ho触类旁通,一下就找到了问题所在:“所以我能够像深度优先搜索那样用一个best(i, j)记录当前搜索过的路径中到达第i层第j个房间时最多能获取多少奖券,然后在一个状态(i, j, k)想要入队的时候,推断k与best(i, j)的大小。假设k小于等于best(i, j)就没有必要进队了~”
“看来你还陷在了死胡同里。你这样在最坏情况复杂度根本没有变化不是?”小Hi无奈道:“你细致想想,依照宽度优先搜索的顺序。是不是一个状态(i, j, k)在拓展出(i', j', k')的时候,(i', j', k')要么从来没有入队列,要么就仍然在队列里?”
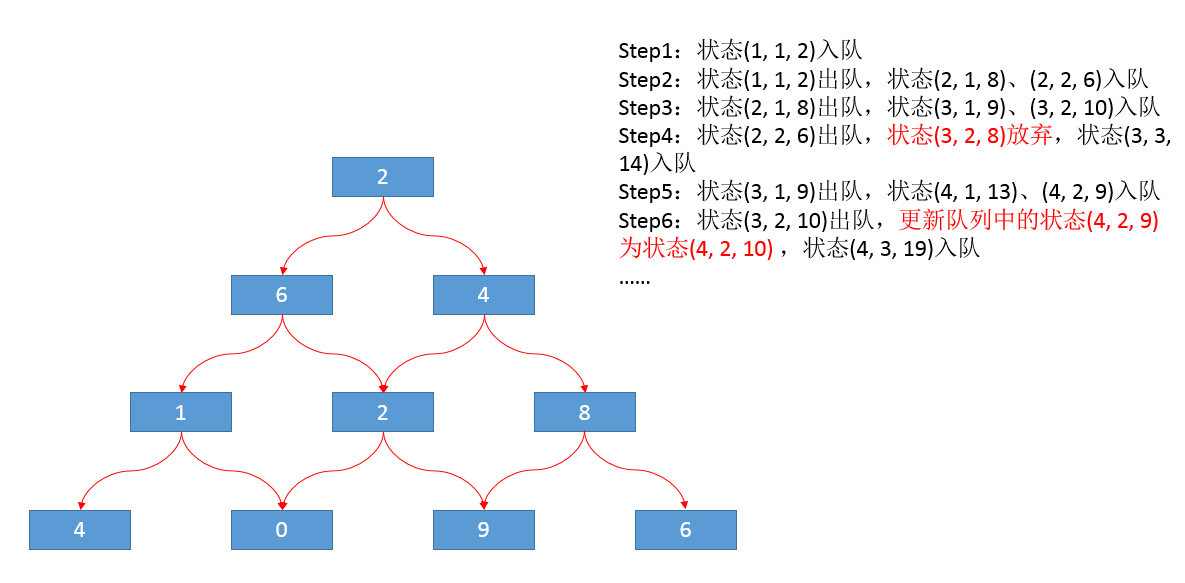
“唔...这个问题看来,基本上就是这样一层一层的顺序出队列的,那还是那个问题,假设我在推断状态(i, j, k)是否应该入队列的时候,发现了k大于best(i, j),这个时候假设我再去推断一下队列中是否有一个(i, j, k')的状态。假设没有。就将(i, j, k)入队列,不然由于k'大于k,那么就像我们之前分析的那样(i, j, k')这个状态时没用的。不如就用k去替换掉状态(i, j, k')中的k'。这样也会降低运算不是?”
“没错~并且你细致分析的话,每一个房间都仅仅会入队列和出队列一次,这样就保证了平均情况时间复杂度和最坏情况时间复杂度都是O(n^2)哦。~”
“原来是这样,那么如今问题差点儿相同攻克了呢!”小Ho高兴道:“赶紧算出来。我好去拿奖品。”
“急什么!
你从这之中可学到了什么知识么?”小Hi拦住了急冲冲的小Ho。问道。
“啊?”
提示三:总结归纳提公式。降低冗余是真理
“且不说深度优先这样一个最坏情况下仍然有问题的方法。我们来说这个宽度优先搜索,我们可以使用best(i, j)来进行优化,无非是由于这个问题存在这样两个性质。
”小Hi道。
“第一便是不管我是通过怎么样的方式到达第i层第j个房间的,我之前做出的选择不会对我之后的选择做出限制与优待。就像假设我规定至少要向右走3次。那么状态就不不过(i, j, k)这样。还要加上一个已经向右走的次数t。那么你认为还能就直接像我们之前的方法进行计算么?假设到达第i层第j个房间的路上向右走过3次了,那么之后的走法就没有不论什么限制,不然就仍会有一个至少要向右走一定次数的限制。
这样对于两个状态(i, j, k, l)和(i,
j, k', l')。我们就不可以直接推断出那个状态是更加好的。
“没错~事实上就是best(i, j)有两个keyword进行參考。而这种话就不是随意两个状态都能够进行比較的了。
”小Ho总结道。
“这种性质被我们称为无后效性,顾名思义。当前的抉择不会对后面抉择产生影响。”
“那第二个性质呢?”
“第二个性质被我们称为反复子问题,在我们之前的样例中。我们将从起点出发到走出迷宫的最优路分解成了两个子问题,其一是从第2层的第1个房间走出迷宫的最优路。其二是从第2层的第2个房间走出迷宫的最优路,仅仅要能算出这两个部分的最优值。我就能够知道从起点出发到走出迷宫的最优路。”小Hi道:”而依照这个方案,这两个子问题都有一个同样的子问题——从第3层的第2个房间出发走出迷宫的最优路。”
“这就是反复的子问题了,而我们的做法就是,反复的子问题仅仅计算一次!也就是说我们要先计算出从起点到达第3层的第2个房间的最优线路,然后再考虑接下来怎么走~”小Ho感觉自己渐渐的把握到了关键之处。
“对的。所以综合这样两个性质。我们能够考虑用best(i, j)表示从起点出发,走到第i层第j个房间出发最多能够获得的奖券数。”小Hi提出了一个新的定义:“那么我们要求的答案,便是全部best(n, j)中最大的那一个对不正确?
“是的,那该怎样求这个呢……”小Ho思索着:“第i层第j个房间能够由第i-1层第j个房间和第i-1层第j-1个房间到达。所以best(i, j) = max{best(i - 1, j - 1), best(i - 1, j)} + rewards(i, j)这样么?”
“是的。这个公式便是我们俗称的状态转移方程,你要做的。就是依照这种顺序,依次计算出每个房间的best(i, j),然后在最后统计全部best(n, j)的最大值,就能够得到答案了。”
“这个过程和宽度优先搜索的确非常像,可是因为顺序是确定了的。我能够用一个两重循环,外层是i从1到n枚举层数。内层是j从1到i枚举房间编号,就能够直接进行计算了!”小Ho道。
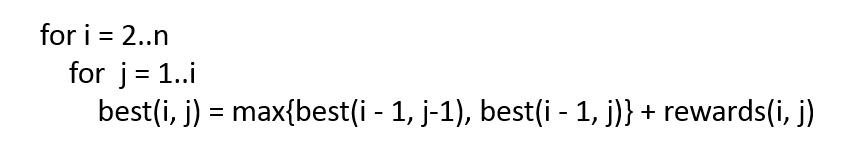
“你这个公式的边界情况还有待考虑嘛,比方j=1的时候就不须要取max了。直接使用best(i - 1, j)计算就可以~”小Hi指出了小Ho存在的一个问题。
“哦~那么j=i的时候也有相似的处理是吧。”
“是的呢。所以快去敲代码吧~”小Hi笑了笑:“抓紧时间。迷宫节就要结束了哦。”
输入
提示三:总结归纳提公式。降低冗余是真理
“且不说深度优先这样一个最坏情况下仍然有问题的方法。我们来说这个宽度优先搜索,我们可以使用best(i, j)来进行优化,无非是由于这个问题存在这样两个性质。
”小Hi道。
“第一便是不管我是通过怎么样的方式到达第i层第j个房间的,我之前做出的选择不会对我之后的选择做出限制与优待。就像假设我规定至少要向右走3次。那么状态就不不过(i, j, k)这样。还要加上一个已经向右走的次数t。那么你认为还能就直接像我们之前的方法进行计算么?假设到达第i层第j个房间的路上向右走过3次了,那么之后的走法就没有不论什么限制,不然就仍会有一个至少要向右走一定次数的限制。
这样对于两个状态(i, j, k, l)和(i, j, k', l')。我们就不可以直接推断出那个状态是更加好的。
“没错~事实上就是best(i, j)有两个keyword进行參考。而这种话就不是随意两个状态都能够进行比較的了。
”小Ho总结道。
“这种性质被我们称为无后效性,顾名思义。当前的抉择不会对后面抉择产生影响。”
“那第二个性质呢?”
“第二个性质被我们称为反复子问题,在我们之前的样例中。我们将从起点出发到走出迷宫的最优路分解成了两个子问题,其一是从第2层的第1个房间走出迷宫的最优路。其二是从第2层的第2个房间走出迷宫的最优路,仅仅要能算出这两个部分的最优值。我就能够知道从起点出发到走出迷宫的最优路。”小Hi道:”而依照这个方案,这两个子问题都有一个同样的子问题——从第3层的第2个房间出发走出迷宫的最优路。”
“这就是反复的子问题了,而我们的做法就是,反复的子问题仅仅计算一次!也就是说我们要先计算出从起点到达第3层的第2个房间的最优线路,然后再考虑接下来怎么走~”小Ho感觉自己渐渐的把握到了关键之处。
“对的。所以综合这样两个性质。我们能够考虑用best(i, j)表示从起点出发,走到第i层第j个房间出发最多能够获得的奖券数。”小Hi提出了一个新的定义:“那么我们要求的答案,便是全部best(n, j)中最大的那一个对不正确?
“是的,那该怎样求这个呢……”小Ho思索着:“第i层第j个房间能够由第i-1层第j个房间和第i-1层第j-1个房间到达。所以best(i, j) = max{best(i - 1, j - 1), best(i - 1, j)} + rewards(i, j)这样么?”
“是的。这个公式便是我们俗称的状态转移方程,你要做的。就是依照这种顺序,依次计算出每个房间的best(i, j),然后在最后统计全部best(n, j)的最大值,就能够得到答案了。”
“这个过程和宽度优先搜索的确非常像,可是因为顺序是确定了的。我能够用一个两重循环,外层是i从1到n枚举层数。内层是j从1到i枚举房间编号,就能够直接进行计算了!”小Ho道。
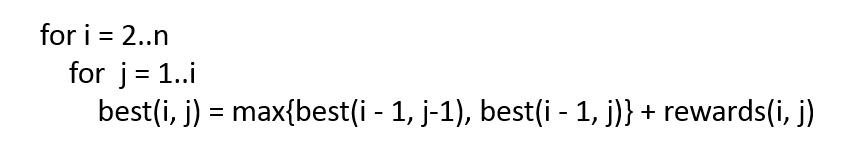
“你这个公式的边界情况还有待考虑嘛,比方j=1的时候就不须要取max了。直接使用best(i - 1, j)计算就可以~”小Hi指出了小Ho存在的一个问题。
“哦~那么j=i的时候也有相似的处理是吧。”
“是的呢。所以快去敲代码吧~”小Hi笑了笑:“抓紧时间。迷宫节就要结束了哦。”
每一个測试点(输入文件)有且仅有一组測试数据。
每组測试数据的第一行为一个正整数n,表示这个迷宫的层数。
接下来的n行描写叙述这个迷宫中每一个房间的奖券数,当中第i行的第j个数代表着迷宫第i层的编号为j的房间中的奖券数量。
測试数据保证。有100%的数据满足n不超过100
对于100%的数据,迷宫的层数n不超过100
对于100%的数据,每一个房间中的奖券数不超过1000
对于50%的数据,迷宫的层数不超过15(小Ho表示2^15才3万多呢,也就是说……)
对于10%的数据,迷宫的层数不超过1(小Hi非常好奇你的边界情况处理的怎样?~)
对于10%的数据。迷宫的构造满足:对于90%以上的结点,左边道路通向的房间中的奖券数比右边道路通向的房间中的奖券数要多。
对于10%的数据,迷宫的构造满足:对于90%以上的结点,左边道路通向的房间中的奖券数比右边道路通向的房间中的奖券数要少。
输出
对于每组測试数据。输出一个整数Ans。表示小Ho能够获得的最多奖券数。





