从Policy Gradient到PPO的来龙去脉

1. PPO算法

$PPO$ 算法全称 $ProximalPolicyOptimization$ ，即近端策略优化算法，该算法是 $OpenAI$ 在 $2017$ 提出的一种强化学习算法，被认为是目前强化学习领域的 $SOTA$ 方法，也是适用性最广的算法之一。

$PPO$ 算法的核心思想是减小策略更新引起的方差，从而提高学习效果。具体来说，$PPO$ 算法通过引入一个近似目标函数和一个重要性采样来减小方差。近似目标函数通过将旧的策略和目标策略的差值限制在一个范围内，减小了方差。重要性采样通过计算旧策略和目标策略之间的比率，减小了方差。

下文将从传统的策略梯度算法开始，逐渐介绍 $PPO$ 算法的来龙去脉。

2. 策略梯度算法

记策略为 $\pi$ ，记策略 $\pi$ 的参数为 $\theta$ ，记状态为 $s$ ，记动作为 $a$ 。

在一场游戏中，把环境的输出和智能体的动作全部组合起来，就是一条轨迹 $\tau$ ：

$$\tau =\{s_1,a_1,s_2,a_2,\cdots ,s_t,a_t\}$$

给定智能体策略参数 $\theta$ ，则可以计算某条轨迹 $\tau$ 发生的概率：

$$\begin{array}{rl}{p}_{\theta }(\tau )& =p\left(s_1\right)p_{\theta }\left(a_1|s_1\right)p(s_2|s_1,a_1)p_{\theta }\left(a_2|s_2\right)p(s_3|s_2,a_2)\cdots \\ & =p\left(s_1\right)\prod _{t=1}^T{p}_{\theta }\left(a_t|s_t\right)p(s_{t+1}|s_t,a_t)\end{array}$$

某个轨迹出现的概率取决于环境的动作和智能体的动作。环境的动作是指环境根据其函数内部的参数或内部的规则采取的动作。 $p(s_{t+1}|s_t,a_t)$ 代表的是环境，通常我们无法控制环境，因为环境是设定好的。我们能控制的是 $p_{\theta }(s_t|a_t)$ 。

奖励函数根据在某一个状态采取的某一个动作决定这个动作可以得到的分数。对奖励函数输入 $s_1$、$a_1$，它会输出 $r_1$ ；输入 $s_2$、$a_2$，奖励函数会输出 $r_2$ 。我们把轨迹所有的奖励 $r$ 都加起来，就得到了 $R(\tau )$ ，其代表某一个轨迹 $\tau$ 的奖励。

$R(\tau )$ 并不只是一个标量，它是一个随机变量，因为智能体在给定同样的状态下会采取什么样的动作，这是有随机性的。环境会怎样变化也是有随机性的，所以 $R(\tau )$ 是一个随机变量。我们能够计算的是 $R(\tau )$ 的期望值，给定某一组参数 $\theta$ ， $R_{\theta }$ 的期望值为：

$${\overline{R}}_{\theta }=\sum _{\tau }R(\tau )p_{\theta }(\tau )$$

我们可以根据 $\theta$ 算出某一个轨迹 $\tau$ 出现的概率，接下来计算 $\tau$ 的总奖励。总奖励使用 $\tau$ 出现的概率进行加权，对所有的 $\tau$ 进行求和，就是期望值：

$${\overline{R}}_{\theta }=\sum _{\tau }R(\tau )p_{\theta }(\tau )={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )]$$

从分布 $p_{\theta }(\tau )$ 采样一个轨迹 $\tau$ ，计算 $R(\tau )$ 的期望值，就是期望奖励，我们要最大化期望奖励，可使用梯度上升法实现。

首先计算 ${\overline{R}}_{\theta }$ 的梯度：

$$\begin{array}{rl}\mathrm{\nabla }{\overline{R}}_{\theta }& =\sum _{\tau }R(\tau )\mathrm{\nabla }{p}_{\theta }(\tau )\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\frac{\mathrm{\nabla }{p}_{\theta }(\tau )}{p_{\theta }(\tau )}\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )\\ & ={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )]\end{array}$$

实际上期望值 ${\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )]$ 无法计算，所以我们用采样的方式采样 $N$ 个 $\tau$ 并计算每一个的值，把每一个的值加起来，就可以得到梯度：

$$\begin{array}{rl}{\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )]& \approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\mathrm{\nabla }\log p_{\theta }\left({\tau }^n\right)\end{array}$$

接下来，可将前面准备好的 $\log p_{\theta }\left({\tau }^n\right)$ 带入上式，为了清晰一些，这里先计算 $\mathrm{\nabla }\log p_{\theta }\left({\tau }^n\right)$ （由于是对 $\theta$ 求导，与 $\theta$ 无关项的梯度为 $0$ ，因此可以省略掉一部分）：

$$\begin{array}{rl}\mathrm{\nabla }\log p_{\theta }(\tau )& =\mathrm{\nabla }(\log p(s_1)+\sum _{t=1}^T\log p_{\theta }(a_t|s_t)+\sum _{t=1}^T\log p(s_{t+1}|s_t,a_t))\\ & =\mathrm{\nabla }\log p(s_1)+\mathrm{\nabla }\sum _{t=1}^T\log p_{\theta }(a_t|s_t)+\mathrm{\nabla }\sum _{t=1}^T\log p(s_{t+1}|s_t,a_t)\\ & =\mathrm{\nabla }\sum _{t=1}^T\log p_{\theta }(a_t|s_t)\\ & =\sum _{t=1}^T\mathrm{\nabla }\log p_{\theta }(a_t|s_t)\end{array}$$

再带入上式，有如下完整过程：

$$\begin{array}{rl}\mathrm{\nabla }{\overline{R}}_{\theta }& =\sum _{\tau }R(\tau )\mathrm{\nabla }{p}_{\theta }(\tau )\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\frac{\mathrm{\nabla }{p}_{\theta }(\tau )}{p_{\theta }(\tau )}\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )\\ & ={\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}[R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )]\\ & \approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\mathrm{\nabla }\log p_{\theta }\left({\tau }^n\right)\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)\end{array}$$

我们可以直观地理解上式，也就是在我们采样到的数据里面，采样到在某一个状态 $s_t$ 要执行某一个动作 $a_t$，$(s_t,a_t)$ 是在整个轨迹 $\tau$ 的里面的某一个状态和动作的对。假设我们在 $s_t$ 执行 $a_t$ ，最后发现 $\tau$ 的奖励是正的，我们就要增加在 $s_t$ 执行 $a_t$ 的概率。反之，我们就要减少在 $s_t$ 执行 $a_t$ 的概率。这可以用梯度上升来实现，记学习率为 $\eta$ ：

$$\theta \leftarrow \theta +\eta \mathrm{\nabla }{\overline{R}}_{\theta }$$

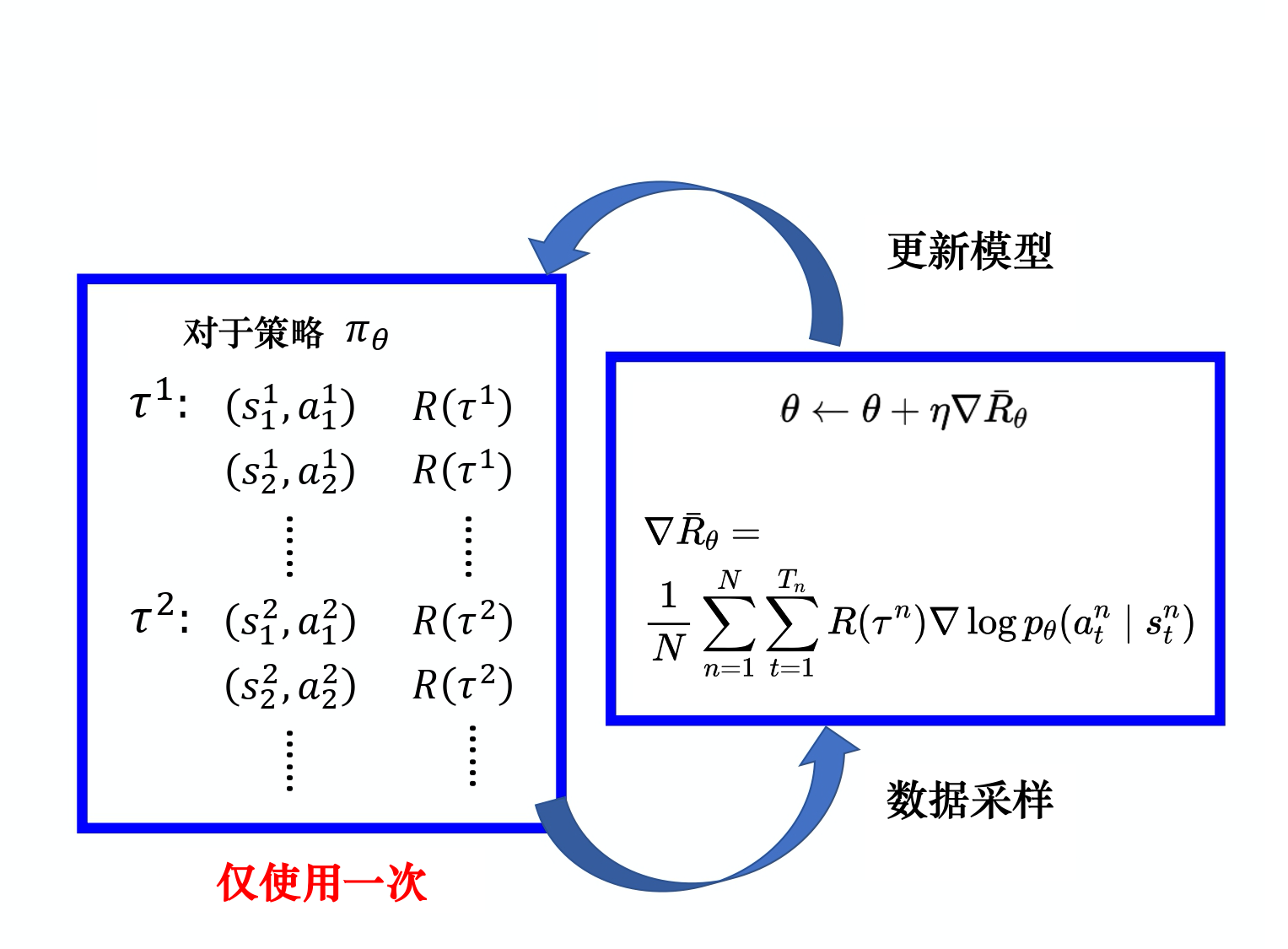
再具体的计算过程中，我们可以先进行几场游戏，每场游戏生成一条轨迹 $\tau$ 以及一个奖励 $R(\tau )$ ，然后我们就可以把采样到的数据代入期望奖励的梯度计算公式，进而使用梯度上升的方法更新模型参数 $\theta$ ，如下图所示：

更新完模型以后，我们要重新采样数据再更新模型。注意，一般策略梯度（policy gradient，PG）采样的数据只会用一次。我们采样这些数据，然后用这些数据更新参数，再丢掉这些数据。接着重新采样数据，才能去更新参数。

3. 策略梯度实现技巧

3.1 技巧：baseline

如果给定状态 $s$ 采取动作 $a$，整场游戏得到正的奖励，就要增加 $(s,a)$ 的概率。如果给定状态 $s$ 执行动作 $a$，整场游戏得到负的奖励，就要减小 $(s,a)$ 的概率。但在很多游戏里面，奖励总是正的，最低都是 0。假设我们直接使用下式，在训练的时候只要整场游戏得到正的奖励，不管是什么动作，都应该要把它的概率提升。

$$\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\log p_{\theta }(a_t^n\mid s_t^n)$$

这显然是有问题的。要怎么解决这个问题呢？我们会希望奖励不总是正的。为了解决奖励总是正的的问题，我们可以把奖励减 $b$，即

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(R\left({\tau }^n\right)-b)\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)$$

其中，$b$ 称为 $baseline$ 。通过这种方法，我们就可以让 $R(\tau )-b$ 这一项有正有负。如果我们得到的总奖励$R(\tau )>b$，就让 $(s,a)$ 的概率上升。如果$R(\tau )<b$，就算$R(\tau )$是正的，值很小也是不好的，我们就让$(s,a)$的概率下降，让这个状态采取这个动作的分数下降。$b$ 怎么设置呢？我们可以对 $\tau$ 的值取期望， 计算 $\tau$ 的平均值，令 $b\approx E[R(\tau )]$ 。

所以在训练的时候，我们会不断地把 $R(\tau )$ 的值记录下来，会不断地计算 $R(\tau )$ 的平均值，把这个平均值当作 $b$ 来使用。 这样就可以让我们在训练的时候，$R(\tau )-b$ 是有正有负的。

事实上 $b$ 通常是一个网络估计出来的，它是一个网络的输出。我们把 $R-b$ 这一项称为优势函数（advantage function）， 用 $A^{\theta }(s_t,a_t)$ 来代表优势函数。优势函数取决于 $s$ 和 $a$，我们就是要计算在某个状态 $s$ 采取某个动作 $a$ 的时候，优势函数的值。优势函数 $A^{\theta }(s_t,a_t)$ 的上标是 $\theta$，$\theta$ 代表用模型 $\theta$ 与环境交互。优势函数的意义是，假设我们在某一个状态 $s_t$ 执行某一个动作 $a_t$，相较于其他可能的动作，$a_t$ 有多好。优势函数在意的不是绝对的好，而是相对的好，即相对优势（relative advantage）。 $A^{\theta }(s_t,a_t)$ 通常可以由一个网络估计出来，这个网络称为评论员（critic）。

3.2 技巧：只考虑动作之后的奖励

在同一场游戏里面，也许有些动作是好的，有些动作是不好的。假设整场游戏的结果是好的，但并不代表这场游戏里面每一个动作都是好的。若是整场游戏结果不好，但并不代表游戏里面的每一个动作都是不好的。所以我们希望可以给每一个不同的动作前面都乘上不同的权重。每一个动作的不同权重反映了每一个动作到底是好的还是不好的。

在理想的状况下，如果我们的采样数据够多，就可以解决这个问题，即采样次数足够多，应该可以分辨出哪些是真正好的动作，哪些是混子。但现在的问题是，我们采样的次数是不够多的。在采样的次数不够多的情况下，我们要给每一个状态-动作对分配合理的分数，要让大家知道它真正的贡献。

一个做法是计算某个状态-动作对的奖励的时候，不把整场游戏得到的奖励全部加起来，只计算从这个动作执行以后得到的奖励。因为这场游戏在执行这个动作之前发生的事情是与执行这个动作是没有关系的，所以在执行这个动作之前得到的奖励都不能算是这个动作的贡献。我们把执行这个动作以后发生的所有奖励加起来，才是这个动作真正的贡献。

这一技巧可以表示为下式：

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(\sum _{t^{\prime }=t}^{T_n}{r}_{t^{\prime }}^n-b)\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)$$

原来的权重是整场游戏的奖励的总和，现在改成从某个时刻 $t$ 开始，假设这个动作是在 $t$ 开始执行的，从 $t$ 一直到游戏结束所有奖励的总和才能代表这个动作的好坏。

接下来更进一步，我们把未来的奖励做一个折扣，即：

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}(\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}\cdot r_{t^{\prime }}^n-b)\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)$$

为什么要把未来的奖励做一个折扣呢？因为虽然在某一时刻，执行某一个动作，会影响接下来所有的结果（有可能在某一时刻执行的动作，接下来得到的奖励都是这个动作的功劳），但在一般的情况下，时间拖得越长，该动作的影响力就越小。

4.REINFORCE：蒙特卡洛策略梯度

4.1 蒙特卡洛和时序差分

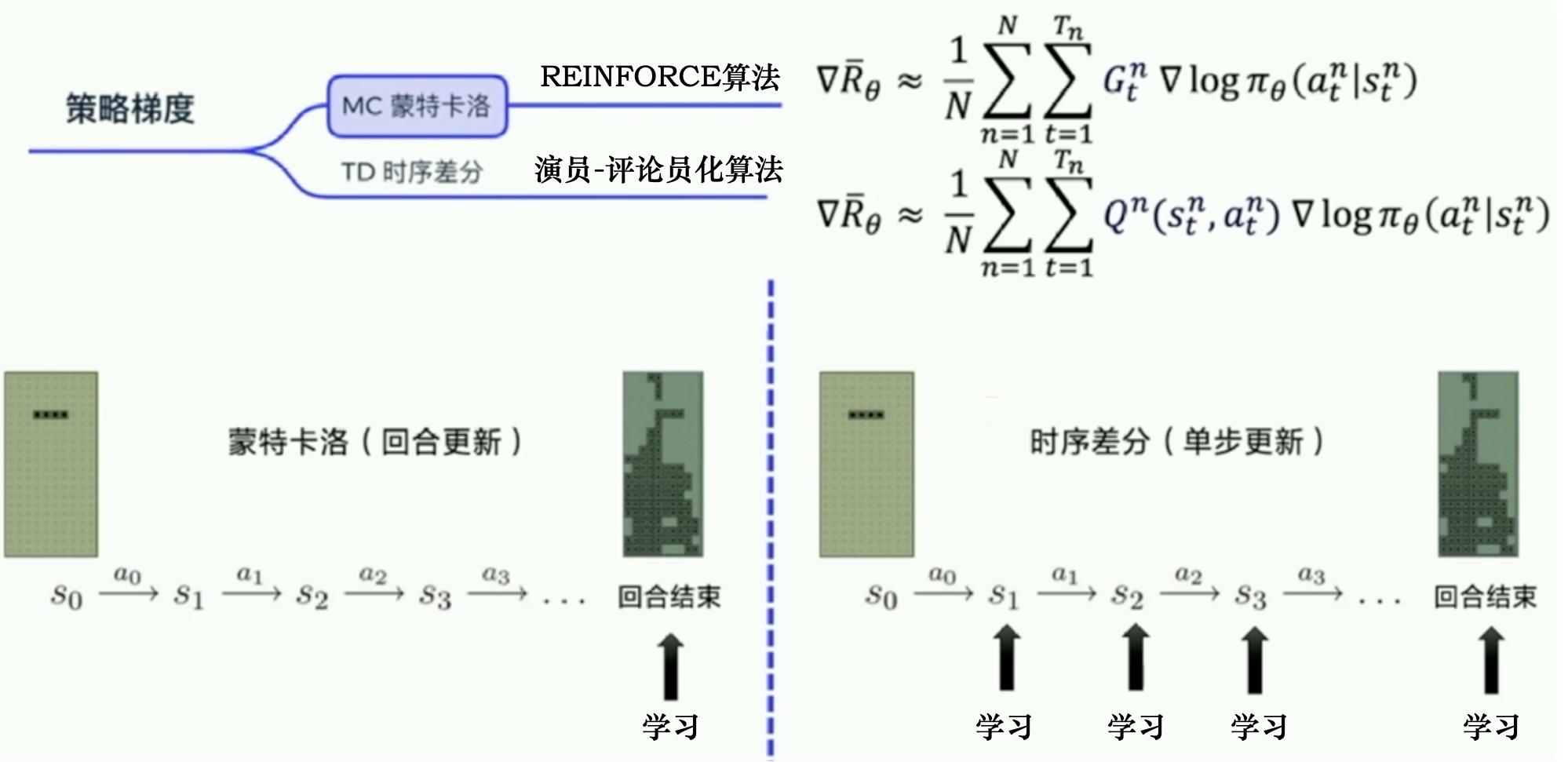
蒙特卡洛方法可以理解为算法完成一个回合之后，再利用这个回合的数据去学习，做一次更新。因为我们已经获得了整个回合的数据，所以也能够获得每一个步骤的奖励，我们可以很方便地计算每个步骤的未来总奖励，即回报 $G_t$ 。$G_t$ 是未来总奖励，代表从这个步骤开始，我们能获得的奖励之和。

相比蒙特卡洛方法一个回合更新一次，时序差分方法是每个步骤更新一次，即每走一步，更新一次，时序差分方法的更新频率更高。时序差分方法使用Q函数来近似地表示未来总奖励 $G_t$。

两种方法的区别如下图所示：

4.2 REINFORCE算法

REINFORCE 用的是回合更新的方式，它在代码上的处理上是先获取每个步骤的奖励，然后计算每个步骤的未来总奖励 $G_t$，将每个 $G_t$ 代入下式进而对策略进行优化：

$$\mathrm{\nabla }{\overline{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}{G}_t^n\mathrm{\nabla }\log {\pi }_{\theta }(a_t^n\mid s_t^n)$$

所以我们在编写代码时会设计一个函数，这个函数的输入是每个步骤获取的奖励，输出是每一个步骤的未来总奖励。因为未来总奖励可写为：

$$\begin{array}{rl}{G}_t& =\sum _{k=t+1}^T{\gamma }^{k-t-1}{r}_k\\ & =r_{t+1}+\gamma G_{t+1}\end{array}$$

即上一个步骤和下一个步骤的未来总奖励的关系如上式所示，所以在代码的计算上，我们是从后往前推，一步一步地往前推，先算 $G_T$，然后往前推，一直算到 $G_1$。

REINFORCTE算法流程如下图所示：

5. 重要性采样

5.1 同策略与异策略

在强化学习里面，如果要学习的智能体和与环境交互的智能体是相同的，我们称之为同策略；如果要学习的智能体和与环境交互的智能体不是相同的，我们称之为异策略。

策略梯度是同策略的算法，对于下式，${\mathbb{E}}_{\tau \sim p_{\theta }(\tau )}$ 是对策略 ${\pi }_{\theta }$ 采样的轨迹 $\tau$ 求期望。一旦更新了参数，从 $\theta$ 变成 ${\theta }^{\prime }$ ，概率 $p_{\theta }(\tau )$ 就不对了，之前采样的数据也不能用了。策略梯度是一个会花很多时间来采样数据的算法，其大多数时间都在采样数据。所以我们想要从同策略变成异策略，这样就可以用另外一个策略 ${\pi }_{{\theta }^{\prime }}$ 、另外一个演员 ${\theta }^{\prime }$ 与环境交互（${\theta }^{\prime }$ 被固定了），用 ${\theta }^{\prime }$ 采样到的数据去训练 $\theta$。

5.2 重要性采样原理

这就需要用到重要性采样了。假设我们有一个函数 $f(x)$，要计算从分布 $p$ 采样 $x$，再把 $x$ 代入 $f$ ，得到 $f(x)$。我们该怎么计算 $f(x)$ 的期望值呢？假设我们不能对分布 $p$ 做积分，但可以从分布 $p$ 采样一些数据 $x^i$。把 $x^i$ 代入 $f(x)$，取它的平均值，就可以近似 $f(x)$ 的期望值，如下式所示：

$${\mathbb{E}}_{x\sim p}[f(x)]\approx \frac{1}{N}\sum _{i=1}^{N}f(x^i)$$

现在有另外一个问题，假设我们不能从分布 $p$ 采样数据，只能从另外一个分布 $q$ 采样数据$x$，$q$ 可以是任何分布。如果我们从 $q$ 采样 $x^i$，就不能使用上式了。因为上式是假设 $x$ 都是从 $p$ 采样出来的。

所以我们做一个修正，期望 ${\mathbb{E}}_{x\sim p}[f(x)]$ 可以写为 $\int f(x)p(x)\mathrm{d}x$ ，我们对其做如下的变换：

$$\int f(x)p(x)\mathrm{d}x=\int f(x)\frac{p(x)}{q(x)}q(x)\mathrm{d}x={\mathbb{E}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$$

则有：

$${\mathbb{E}}_{x\sim p}[f(x)]={\mathbb{E}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$$

由此，我们就可以用在 $q$ 分布中采样出来的 $x$ 取期望值，从 $q$ 里面采样 $x$，再计算 $f(x)\frac{p(x)}{q(x)}$，再取期望值。所以就算我们不能从 $p$ 里面采样数据，但只要能从 $q$ 里面采样数据，就可以计算从 $p$ 采样 $x$ 代入 $f$ 以后的期望值。

因为是从 $q$ 采样数据，所以我们从 $q$ 采样出来的每一笔数据，都需要乘一个重要性权重（importance weight） $\frac{p(x)}{q(x)}$ 来修正这两个分布的差异。$q(x)$ 可以是任何分布，唯一的限制就是 $q(x)$ 的概率是 0 的时候，$p(x)$ 的概率也要为 0，不然会没有定义。

但是，重要性采样有一些问题：虽然我们可以把 $p$ 换成任何的 $q$，但是在实现上， $p$ 和 $q$ 的差距不能太大。如果差距太大，虽然从 $p$ 中采样计算 $f(x)$ 的期望和从 $q$ 中采样计算 $f(x)\frac{p(x)}{q(x)}$ 的期望是相等的，但如果不是计算期望值，而是计算方差， ${\mathrm{Var}}_{x\sim p}[f(x)]$ 和 ${\mathrm{Var}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$ 是不一样的。两个随机变量的期望相同，并不代表它们的方差相同。

可以将 $f(x)$ 和 $f(x)\frac{p(x)}{q(x)}$ 代入方差的公式 $\mathrm{Var}[X]=E\left[X^2\right]-(E[X]{)}^2$，有下式：

$${\mathrm{Var}}_{x\sim p}[f(x)]={\mathbb{E}}_{x\sim p}[f(x{)}^2]-{({\mathbb{E}}_{x\sim p}[f(x)])}^2$$

$$\begin{array}{rl}{\mathrm{Var}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]& ={\mathbb{E}}_{x\sim q}\left[{(f(x)\frac{p(x)}{q(x)})}^2\right]-{\left({\mathbb{E}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\right)}^2\\ & ={\mathbb{E}}_{x\sim q}[f(x{)}^2\frac{p(x{)}^2}{q(x{)}^2}]-{({\mathbb{E}}_{x\sim p}[f(x)])}^2\\ & =\int f(x{)}^2\frac{p(x{)}^2}{q(x{)}^2}q(x)dx-{({\mathbb{E}}_{x\sim p}[f(x)])}^2\\ & =\int f(x{)}^2\frac{p(x)}{q(x)}p(x)dx-{({\mathbb{E}}_{x\sim p}[f(x)])}^2\\ & ={\mathbb{E}}_{x\sim p}[f(x{)}^2\frac{p(x)}{q(x)}]-{({\mathbb{E}}_{x\sim p}[f(x)])}^2\end{array}$$

从上式看出，${\mathrm{Var}}_{x\sim p}[f(x)]$ 和 ${\mathrm{Var}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$ 的差别在于第一项， ${\mathrm{Var}}_{x\sim q}[f(x)\frac{p(x)}{q(x)}]$ 的第一项多乘了$\frac{p(x)}{q(x)}$，如果 $\frac{p(x)}{q(x)}$ 很大，$f(x)\frac{p(x)}{q(x)}$ 的方差就会很大。所以虽然理论上它们的期望值一样，也就是，我们只要对分布 $p$ 采样足够多次，对分布 $q$ 采样足够多次，得到的结果会是一样的。但是如果我们采样的次数不够多，因为它们的方差差距是很大的，所以我们就有可能得到差别非常大的结果。

5.3 应用重要性采样实现异策略训练

现在要做的就是把重要性采样用在异策略的情况中，把同策略训练的算法改成异策略训练的算法。之前我们用策略 ${\pi }_{\theta }$ 与环境交互，采样出轨迹 $\tau$，计算 $R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )$ 。现在我们不用 $\theta$ 与环境交互，假设有另外一个策略 ${\pi }_{\theta }^{\prime }$，它的工作就是做示范（demonstration），告诉 $\theta$ 它与环境交互会发生什么事，借此来训练 $\theta$。

我们要训练的是 $\theta$ ，${\theta }^{\prime }$ 只负责做示范，负责与环境交互。我们现在的 $\tau$ 是从 ${\theta }^{\prime }$ 采样出来的，是用 ${\theta }^{\prime }$ 与环境交互。$\theta$ 和 ${\theta }^{\prime }$ 这两个分布不一样，但没有关系，假设我们本来是从 $p$ 采样，但发现不能从 $p$ 采样，可以把 $p$ 换成 $q$，在后面补上一个重要性权重。同理，我们把 $\theta$ 换成 ${\theta }^{\prime }$ 后，要补上一个重要性权重 $\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}$ 。这个重要性权重就是某一个轨迹 $\tau$ 用 $\theta$ 算出来的概率除以这个轨迹 $\tau$ 用 ${\theta }^{\prime }$ 算出来的概率。这一项是很重要的，因为 ${\theta }^{\prime }$ 见到的情形与 $\theta$ 见到的情形可能不是一样的，所以中间要有一个修正的项。如下式所示：

$$\mathrm{\nabla }{\overline{R}}_{\theta }={\mathbb{E}}_{\tau \sim p_{{\theta }^{\prime }(\tau )}}[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )]$$

根据前文中介绍的策略梯度方法的两个技巧，实际在做策略梯度的时候，我们并不是给整个轨迹 $\tau$ 一样的分数，而是将每一个状态-动作对分开计算。实际更新过程中使用的梯度可写为：

$$\mathrm{\nabla }{\overline{R}}_{\theta }={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{\theta }}[A^{\theta }(s_t,a_t)\mathrm{\nabla }\log p_{\theta }\left(a_t^n|s_t^n\right)]$$

在优势函数 $A^{\theta }(s_t,a_t)$ 后面乘 $\mathrm{\nabla }\log p_{\theta }\left(a_t^n|s_t^n\right)$，也就是如果 $A^{\theta }(s_t,a_t)$ 是正的，就要增大概率；如果是负的，就要减小概率。

我们通过重要性采样把同策略变成异策略，从 $\theta$ 变成 ${\theta }^{\prime }$。所以现在 $s_t$、$a_t$ 是 ${\theta }^{\prime }$ 与环境交互以后所采样到的数据。 但是训练时，要调整的参数是模型 $\theta$。因为 ${\theta }^{\prime }$ 与 $\theta$ 是不同的模型，所以我们要有一个修正的项。这个修正的项，就是用重要性采样的技术，把 $s_t$、$a_t$ 用 $\theta$ 采样出来的概率除以 $s_t$、$a_t$ 用 ${\theta }^{\prime }$ 采样出来的概率。因此策略更新过程中使用的梯度可写为：

$$\mathrm{\nabla }{\overline{R}}_{\theta }={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }(s_t,a_t)}{p_{{\theta }^{\prime }}(s_t,a_t)}{A}^{\theta }(s_t,a_t)\mathrm{\nabla }\log p_{\theta }\left(a_t^n|s_t^n\right)]$$

其中，$A^{\theta }(s_t,a_t)$ 有一个上标 $\theta$，$\theta$ 代表 $A^{\theta }(s_t,a_t)$ 是演员 $\theta$ 与环境交互的时候计算出来的。但是实际上从 $\theta$ 换到 ${\theta }^{\prime }$ 的时候，$A^{\theta }(s_t,a_t)$ 应该改成 $A^{{\theta }^{\prime }}(s_t,a_t)$，之前是 $\theta$ 与环境交互，所以我们观察到的是 $\theta$ 可以得到的奖励。但现在是 ${\theta }^{\prime }$ 与环境交互，所以我们得到的这个优势是根据 ${\theta }^{\prime }$ 所估计出来的优势。但目前先假设 $A^{\theta }(s_t,a_t)$ 和 $A^{{\theta }^{\prime }}(s_t,a_t)$ 可能是差不多的。

拆解 $p_{\theta }(s_t,a_t)$ 和 $p_{{\theta }^{\prime }}(s_t,a_t)$ ：

$$\begin{array}{rl}{p}_{\theta }(s_t,a_t)& =p_{\theta }\left(a_t|s_t\right)p_{\theta }(s_t)\\ p_{{\theta }^{\prime }}(s_t,a_t)& =p_{{\theta }^{\prime }}\left(a_t|s_t\right)p_{{\theta }^{\prime }}(s_t)\end{array}$$

于是有：

$$\mathrm{\nabla }{\overline{R}}_{\theta }={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}\frac{p_{\theta }\left(s_t\right)}{p_{{\theta }^{\prime }}\left(s_t\right)}{A}^{{\theta }^{\prime }}(s_t,a_t)\mathrm{\nabla }\log p_{\theta }\left(a_t^n|s_t^n\right)]$$

假设模型是 $\theta$ 的时候，我们看到 $s_t$ 的概率，与模型是 ${\theta }^{\prime }$ 的时候，我们看到 $s_t$ 的概率是一样的，即 $p_{\theta }(s_t)=p_{{\theta }^{\prime }}(s_t)$。因为$p_{\theta }(s_t)$和$p_{{\theta }^{\prime }}(s_t)$是一样的，所以有：

$$\mathrm{\nabla }{\overline{R}}_{\theta }={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}(s_t,a_t)\mathrm{\nabla }\log p_{\theta }\left(a_t^n|s_t^n\right)]$$

为什么我们可以假设 $p_{\theta }(s_t)$ 和 $p_{{\theta }^{\prime }}(s_t)$ 是一样的？
因为我们会看到状态往往与采取的动作是没有太大的关系的。但更直接的理由就是 $p_{\theta }(s_t)$ 很难算， $p_{\theta }(s_t)$ 有一个参数 $\theta$ ，它表示的是我们用 $\theta$ 去与环境交互，计算 $s_t$ 出现的概率，而这个概率很难算。尤其是如果输入的是图片，同样的 $s_t$ 可能根本就不会出现第二次。我们根本没有办法估计 $p_{\theta }(s_t)$ ，所以干脆就无视这个问题。

$p_{\theta }(a_t|s_t)$很好算，我们有参数 $\theta$ ，它就是一个策略网络。我们输入状态 $s_t$ 到策略网络中，它会输出每一个 $a_t$ 的概率。所以我们只要知道 $\theta$ 和 ${\theta }^{\prime }$ 的参数就可以计算 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}$。

接下来，可以从上式中的目标函数梯度反推出优化的目标函数，根据 $\mathrm{\nabla }f(x)=f(x)\mathrm{\nabla }\log f(x)$（由于$\mathrm{\nabla }\log f(x)=\frac{\mathrm{\nabla }f(x)}{f(x)}$）。同时需注意，对 $\theta$ 求梯度时，$p_{{\theta }^{\prime }}(a_t|s_t)$ 和 $A^{{\theta }^{\prime }}(s_t,a_t)$ 都是常数。所以得到当我们使用重要性采样的时候，要去优化的目标函数为：

$$J^{{\theta }^{\prime }}(\theta )={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}(s_t,a_t)\right]$$

我们将其记为 $J^{{\theta }^{\prime }}(\theta )$，因为$J^{{\theta }^{\prime }}(\theta )$ 括号里面的 $\theta$ 代表我们要去优化的参数。${\theta }^{\prime }$ 是指我们用 ${\theta }^{\prime }$ 做示范，就是现在真正在与环境交互的是 ${\theta }^{\prime }$。用 ${\theta }^{\prime }$ 与环境交互，采样出 $s_t$、$a_t$ 以后，要去计算 $s_t$ 与 $a_t$ 的优势 $A^{{\theta }^{\prime }}(s_t,a_t)$，再用它乘 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}$ 进行修正。

6. 近端策略优化（PPO）

6.1 原始PPO算法

可以通过重要性采样把同策略换成异策略，但重要性采样有一个问题：如果 $p_{\theta }\left(a_t|s_t\right)$ 与 $p_{{\theta }^{\prime }}\left(a_t|s_t\right)$ 这两个分布相差太多，重要性采样的结果就会不好。怎么避免它们相差太多呢？这就是 PPO 要做的事情。

在训练的时候，应多加一个约束（constrain）。这个约束是 $\theta$ 与 ${\theta }^{\prime }$ 输出的动作的 KL 散度（KL divergence），这一项用于衡量 $\theta$ 与 ${\theta }^{\prime }$ 的相似程度。我们希望在训练的过程中，学习出的 $\theta$ 与 ${\theta }^{\prime }$ 在行为上比较相似。因为如果 $\theta$ 与 ${\theta }^{\prime }$ 不相似，重要性采样的结果就会不好。所以在 PPO 算法的目标函数分为两项：一项是本来要优化的目标函数 $J^{{\theta }^{\prime }}(\theta )$ ，另一项是对策略差距的约束，目标函数如下式：

$$\begin{array}{rl}& J_{\mathrm{PPO}}^{{\theta }^{\prime }}(\theta )=J^{{\theta }^{\prime }}(\theta )-\beta \mathrm{KL}(\theta ,{\theta }^{\prime })\\ & J^{{\theta }^{\prime }}(\theta )={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }^{\prime }}(a_t\mid s_t)}{A}^{{\theta }^{\prime }}(s_t,a_t)\right]\end{array}$$

注意，PPO 目标函数中加入了 KL 散度的约束，行为策略 ${\theta }^{\prime }$ 和目标策略 $\theta$ 非常接近，PPO 的行为策略和目标策略可认为是同一个策略，因此 PPO 是同策略算法。

所谓的 $\theta$ 与 ${\theta }^{\prime }$ 的距离并不是参数上的距离，而是行为（behavior）上的距离。假设有两个策略 $\theta$ 和 ${\theta }^{\prime }$，所谓参数上的距离就是计算这两组参数有多相似，而行为距离（behavior distance）是，给定同样的状态，输出动作之间的差距。这两个动作的分布都是概率分布，所以我们可以计算这两个概率分布的 KL 散度。把不同的状态输出的这两个分布的 KL 散度的平均值就是我们所指的两个策略之间的 KL 散度。

信任区域策略优化（TRPO）

PPO 有一个前身：信任区域策略优化（trust region policy optimization，TRPO）， TRPO 的优化目标函数为：

$$\begin{array}{r}{J}_{\mathrm{TRPO}}^{{\theta }^{\prime }}(\theta )={\mathbb{E}}_{(s_t,a_t)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}(s_t,a_t)\right],\mathrm{KL}(\theta ,{\theta }^{\prime })<\delta \end{array}$$

很明显，TRPO 与 PPO 的不同在于约束所在的位置不一样，PPO 直接把约束放到要优化的式子里面，我们就可以用梯度上升的方法去最大化目标函数；但 TRPO 是把 KL 散度当作约束，它希望 $\theta$ 与 ${\theta }^{\prime }$ 的 KL 散度小于 $\delta$。如果我们使用的是基于梯度的优化，有约束是很难处理的。因此我们一般就使用 PPO，而不使用 TRPO 。PPO 与 TRPO 的性能差不多，但 PPO 在实现上比 TRPO 容易得多。

近端策略优化惩罚（PPO1）

PPO1 算法先初始化一个策略的参数 ${\theta }^0$。在每一个迭代里面，我们用前一个训练的迭代得到的演员的参数 ${\theta }^k$ 与环境交互，采样到大量状态-动作对。根据 ${\theta }^k$ 交互的结果，我们估测$A^{{\theta }^k}(s_t,a_t)$ ，再使用 PPO 的优化公式对策略进行优化，优化的目标函数为：

$$J_{\mathrm{PPO}}^{{\theta }^k}(\theta )=J^{{\theta }^k}(\theta )-\beta \mathrm{KL}(\theta ,{\theta }^k)$$

在 PPO 的论文里面还有一个技巧：自适应KL散度（adaptive KL divergence）。PPO 算法中有一个问题，即 $\beta$ 的取值问题。自适应KL散度是一个动态调整 $\beta$ 的方法。我们设一个可以接受的 KL 散度的最大值，假设优化完上式以后，KL 散度的值太大，这就代表后面惩罚的项 $\beta \mathrm{KL}(\theta ,{\theta }^k)$ 没有发挥作用，我们就把 $\beta$ 增大；另外，我们再设一个 KL 散度的最小值，如果优化完上式以后，KL 散度比最小值还要小，就代表后面这一项的效果太强了，我们怕他只优化后一项，使 $\theta$ 与 ${\theta }^k$ 一样，这不是我们想要的，所以要减小 $\beta$ 。$\beta$ 是可以动态调整的，因此称之为自适应 KL 惩罚（adaptive KL penalty）。总结：如果 $\mathrm{KL}(\theta ,{\theta }^k)>{\mathrm{KL}}_{max}$，增大 $\beta$；如果 $\mathrm{KL}(\theta ,{\theta }^k)<{\mathrm{KL}}_{min}$，减小 $\beta$ 。

这种近端策略优化惩罚（PPO1）算法可以完整表示为：

$$\begin{array}{rl}& J_{\text{PPO}}^{{\theta }^k}(\theta )=J^{{\theta }^k}(\theta )-\beta \text{KL}(\theta ,{\theta }^k)\\ & J^{{\theta }^k}(\theta )\approx \sum _{(s_t,a_t)}\frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }^k}(a_t\mid s_t)}{A}^{{\theta }^k}(s_t,a_t)\end{array}$$

近端策略优化裁剪（PPO2）

PPO1 中计算 KL 散度比较复杂，还有一个 PPO2算法，近端策略优化裁剪，PPO2 的目标函数里面没有 KL 散度，其要最大化的目标函数为：

$$\begin{array}{rl}{J}_{\mathrm{PPO}2}^{{\theta }^k}(\theta )\approx \sum _{(s_t,a_t)}min& (\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}{A}^{{\theta }^k}(s_t,a_t),\mathrm{clip}(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)},1-\epsilon ,1+\epsilon )A^{{\theta }^k}(s_t,a_t))\end{array}$$

其中，$\epsilon$ 是一个超参数，是我们要调整的，可以设置成 0.1 或 0.2。

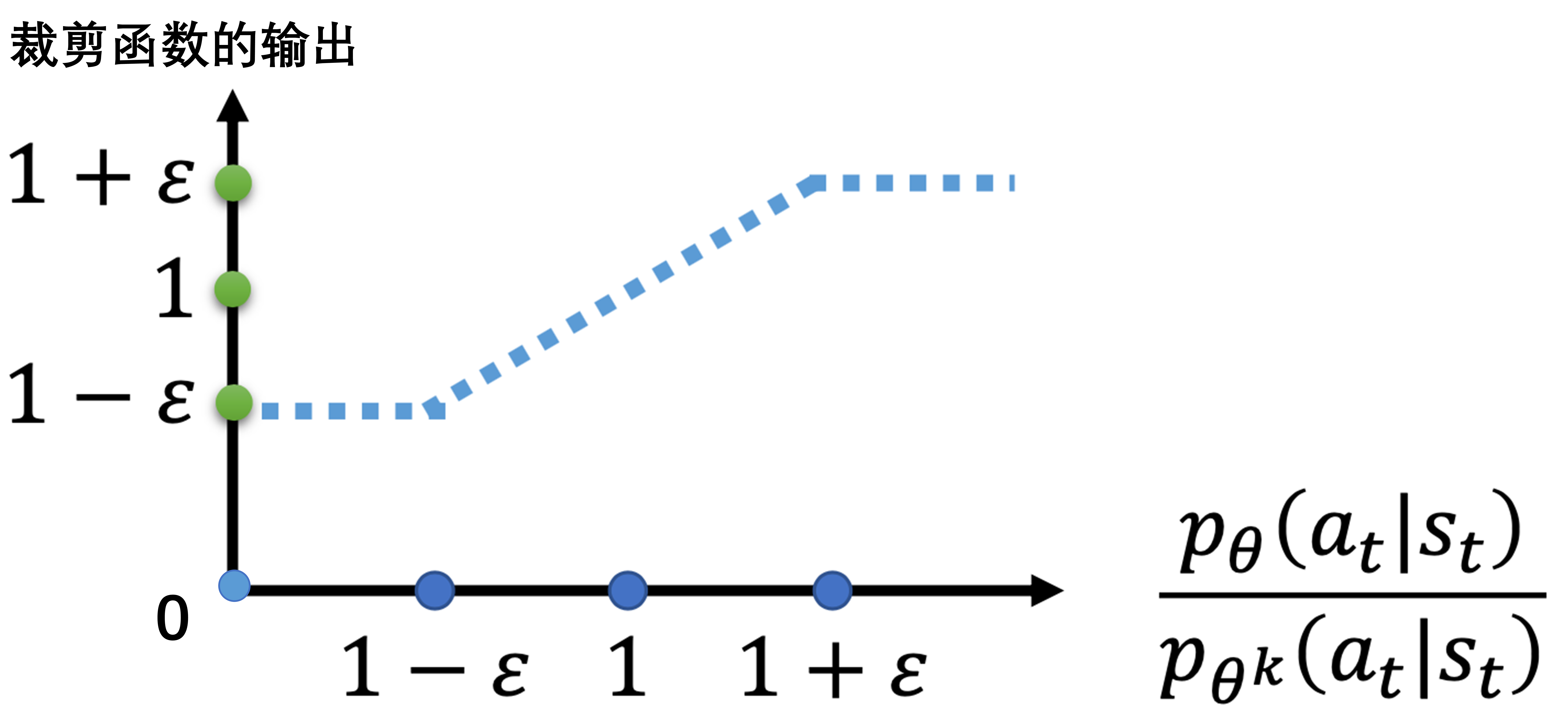
接下来分析裁剪函数的输出：

$$\mathrm{clip}(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)},1-\epsilon ,1+\epsilon )$$

如果不考虑与裁剪函数相乘的优势函数 $A$ ，则裁剪函数的输出很简单，如下图所示：

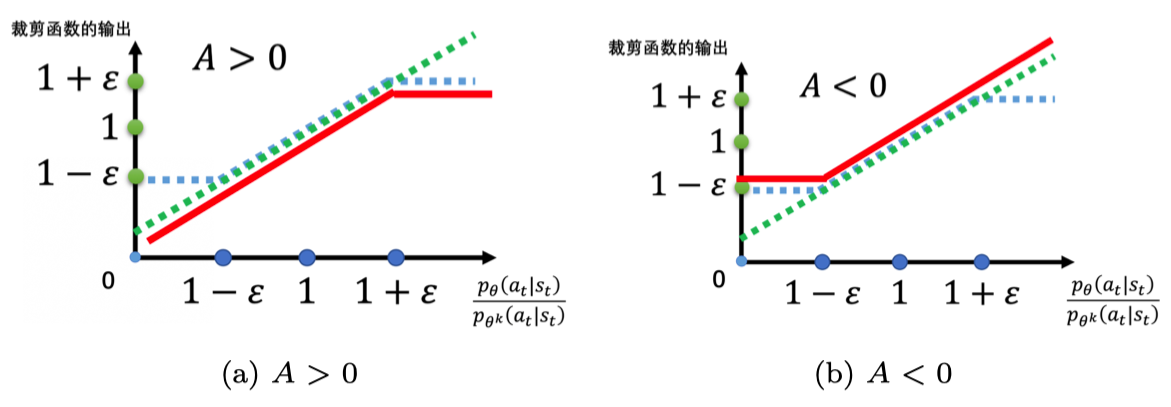
如果考虑与裁剪函数相乘的优势函数 $A$ ，则虽然裁剪函数的值并不受优势函数 $A$ 影响，但是由于前后两项需要取最小值，因此裁剪函数的输出最终体现在目标函数上的值会受到优势函数 $A$ 的正负的影响。如下图所示，假设裁剪函数后面乘上的项 $A>0$ ，则如左图（a）所示，取最小的结果就是红色的这条线；假设裁剪函数后面乘上的项 $A<0$ ，则如右图（b）所示，取最小结果就是红色的这条线。

上面给出的目标函数看似复杂，实际想要做的就是希望 $p_{\theta }(a_t|s_t)$ 与 $p_{{\theta }^k}(a_t|s_t)$比较接近。

• 如果 $A>0$ ，也就是某一个状态-动作对是好的，我们希望增大这个状态-动作对的概率。也就是，我们想让 $p_{\theta }(a_t|s_t)$ 越大越好，但它与 $p_{{\theta }^k}(a_t|s_t)$ 的比值不可以超过 $1+\epsilon$。所以在训练的时候，当 $p_{\theta }(a_t|s_t)$ 被训练到 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}>1+\epsilon$ 时，就会停止。
• 如果 $A<0$ ，也就是某一个状态-动作对是不好的，那么我们希望把 $p_{\theta }(a_t|s_t)$ 减小，减到 $\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}$ 是 $1-\epsilon$ 的时候停止，此时不用再减得更小。