Matlab系统辨识
建立系统的数学模型
(1)使用tf函数建立传递函数模型
对于下面这个传递函数:

第一种模型建立方式:
num = [12 15]
den = [1 16 64 192];
G = tf(num, den)
其中num为分子多项式的系数,den为分母多项式的系数。
第二种模型建立方式:
s = tf('s');
G = (12*s+15)/(s^3+16*s^2+64*s+192)
代码s = tf('s');表示用s这个变量来代表一个拉什算子s。
对于一个带有时延的传递函数模型,也可以使用tf函数来进行设置:
G = tf(1,[1 1],'inDelay',5)
通过设置tf函数的'inDelay'参数为5,建立了一个带有5秒延时的系统:

也同样可以使用s = tf('s');的方式进行建立:
G = exp(-5*s)/(s+1)
另外,有时候分子或分母的多项式是多项式相乘的形式,比如下面的这个传递函数:
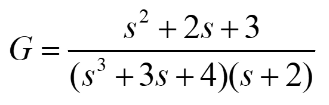
这时可直接使用卷积函数(conv)来简化建立过程:
num = [1 2 3];
den = conv([1 0 3 4],[1 2]);
G = tf(num,den)
(2)使用zpk函数建立传递函数模型(零极点模型)
对于下面这个传递函数:
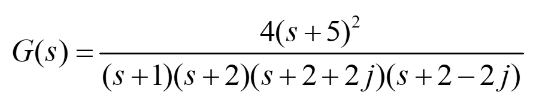
z = [-5 -5];
p = [-1 -2 -2-2*i -2+2*i];
k = 4;
G = zpk(z,p,k)
会在matlab中得到这样的传递函数:
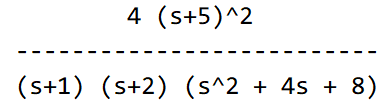
其中复数零极点会被自动乘起来,因为在matlab中无法显示复数的i或j。
使用函数pzmap绘制零极点:
pzmap(G)
绘制结果如下图所示:
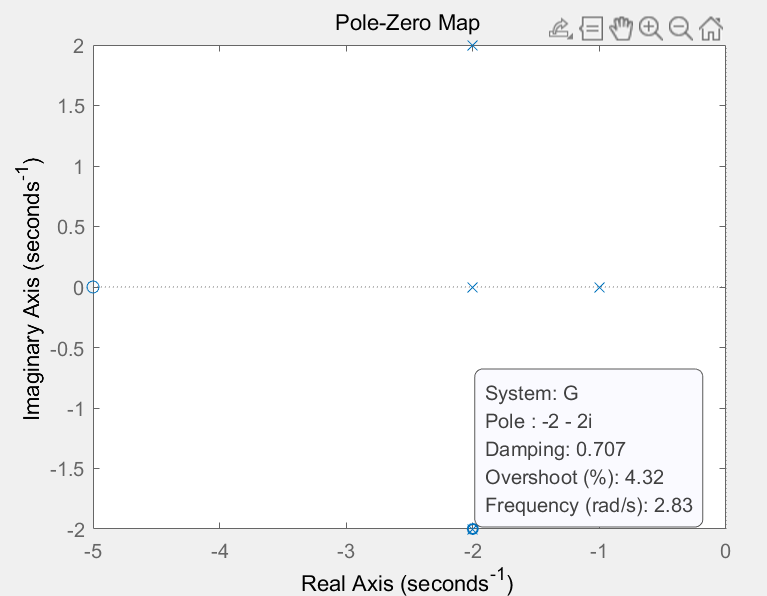
(3)传递函数模型间的变换
已知传递函数获得模型的零极点向量:
G = tf([7 2 8],[4 12 4 2]);
[z,p,k] = zpkdata(G,'v')
使用函数zpkdata,传入系统的传递函数模型,其中'v'表示用向量的形式进行表示。
输出的结果如下:

进而可以得到系统的零极点模型:
G1 = zpk(z,p,k)
(4)使用ss函数建立状态空间模型
对于如下的状态空间模型:

使用ss函数在matlab中建立模型:
A = [6 5 4; 1 0 0; 0 1 0];
B = [1 0 0]';
C = [0 6 7];
D = 0;
G = ss(A,B,C,D)
(5)状态空间模型与传递函数模型之间的转换
对于上一小节建立的状态空间模型,直接使用tf函数转化为传递函数模型:
G1 = tf(G)
反之,也可以使用ss函数将传递函数模型转换回状态空间模型:
G2 = ss(G1)
但是需要注意的是,我们将一个模型使用tf函数转换为传递函数模型之后,再使用ss函数将其转换回状态空间模型,可能会与原模型不太一样。
这是因为在matlab中,默认会将系统转化为一个能观型的状态空间模型,而不是我们平时会写成的能控标准型的形式(可以自己写一个函数来实现它)。
最小二乘参数辨识方法
(1)系统辨识基础
辨识问题分为模型结构辨识和参数辨识,其中模型结构辨识会用到《数值分析》课程中的方法。当系统模型结构根据工程经验或采用模型结构的辨识方法确定后,主要的问题就是模型的参数估计。
系统辨识的主要内容和步骤:
① 设法取得系统输入输出的观测数据:设计准则、持续激励输入信号的设计、采样间隔的设计
② 应该有一个合适的模型集
③ 必须有一个对辨识所得到模型的验证评价:利用先验知识验证、利用数据检验、利用实际响应检验、利用激励信号的自相关函数检验
(2)最小二乘法LSM(Least Squares Method)简单原理及应用
最小二乘法原理:未知量的最可能值是使各项实际观测值和计算值之间差的平方乘以其精确度的数值以后的和最小。
也就是说:
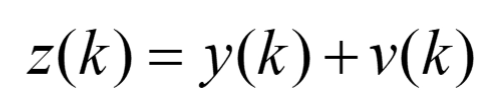
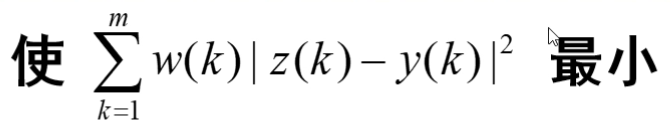
下面举一个例子说明算法原理:
通过试验确定热敏电阻阻值和温度之间的关系:
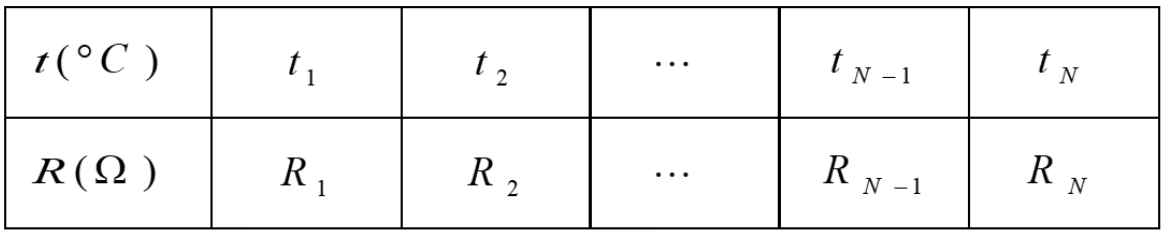
其中R = a + bt。


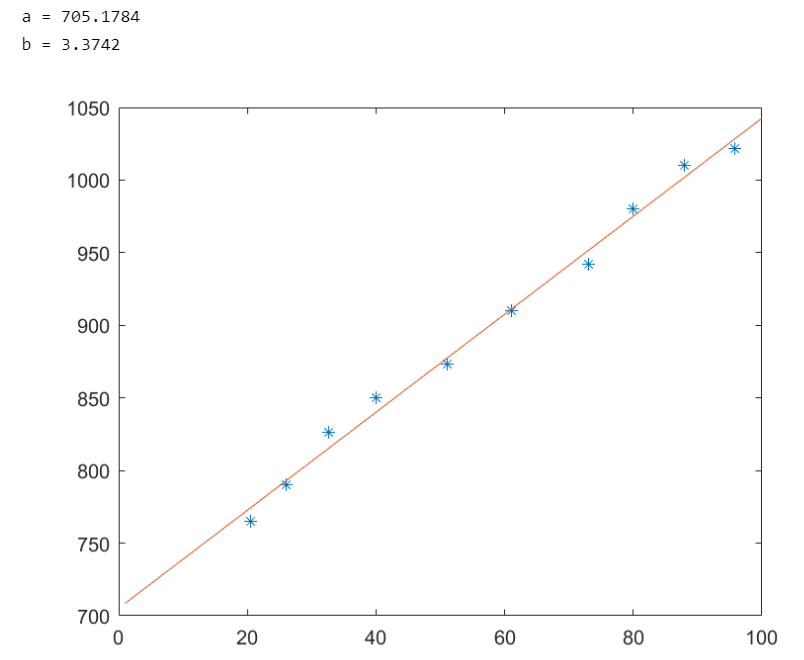
对于上面的例子,在matlab中实现并进行计算:
clear;
t = [20.5 26 32.7 40 51 61 73 80 88 95.7];
R = [765 790 826 850 873 910 942 980 1010 1022];
figure;
plot(t,R,"*");
hold on;
N = numel(t);
%最小二乘法拟合线性模型参数
den = N*sum(t.^2) - sum(t)^2;
a = (sum(R)*sum(t.^2) - sum(R.*t)*sum(t))/den
b = (N*sum(R.*t) - sum(R)*sum(t))/den
%绘制拟合直线
t1 = 1:100;
R1 = a + b*t1;
plot(t1, R1);
%计算温度t2 = 70对应的组织
t2 = 70;
R2 = a + b*t2
补充:如果希望将数据点连接起来,可以将plot语句改成:plot(t,R,"*-");
输出结果如下:
(3)LSM在控制系统建模中的应用
算法原理:




注意事项:

伪随机序列(M序列)的产生:
matlab代码:
clear;
n = 4; %四个移位寄存器
L = 2^n-1; %M序列的周期
mag = 5; %M序列的幅值
y1 = 1; y2 = 1; y3 = 1; y4 = 0; %四个移位寄存器的初始值
for i = 1:L
x1 = xor(y3,y4);
x2 = y1;
x3 = y2;
x4 = y3;
y(i) = y4;
if y(i) > 0.5
u(i) = -mag;
else
u(i) = mag;
end
y1 = x1;
y2 = x2;
y3 = x3;
y4 = x4;
end
figure(1); stem(u); grid on;
title('输入如信号M序列')
生成的信号如下:

应用实例:


