傅里叶级数推导与理解
本文主要参考:
1、傅里叶级数的由来
傅里叶级数最早提出是想用三角函数的线性组合去表达一个复杂函数。
既然是线性组合,根据线性代数的理论来说,我们最好用彼此线性无关的量去线性表示另一个量,这种情况下会比较方便,而三角函数系的正交性正好满足彼此无关这一个条件。
因此我们可以比较自然地理解这个原始形式的公式:
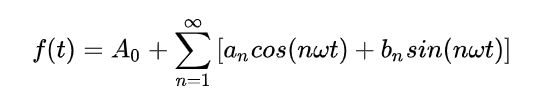
那么三角函数的正交到底是什么意思呢?
2、三角函数的正交性
向量的正交在线性代数的理论中有非常完整简洁的定义:两个向量点积之后结果为0即说明两相量正交。
比如向量a(a1,a2,a3)与向量b(b1,b2,b3)正交,则a1b1+a2b2+a3b3=0。
可以看出向量的点积其实是对应分量相乘再累加的过程,而这种关系与连续函数的正交定义是有密切联系的。
三角函数系的正交定义,比如cosx,与sinx正交,则写成如下形式:
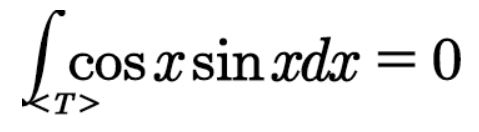
而其实积分的过程可以看做cosx和sinx分别在某个点的取值后相乘再对应累加(积分)。
说具体些,假设我这里积分周期选择0-T,定义一个无穷小的数ξ,则积分可以近似看做如下过程:
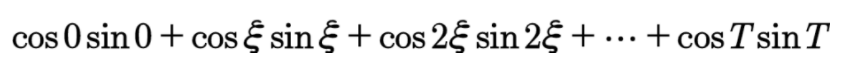
可以看出来这种关系与相量正交的形式是相同的,所以可以认为两个函数相乘积分结果为0则两函数正交。
而可以证明三角函数系(1,cosx,sinx,cos2x,sin2x,…,cosnx,sinnx,…)的正交关系,如果这一堆函数(包括常数1)中任何两个不同函数的乘积在区间[-π, π]上的积分等于零,就说三角函数系在区间[-π, π]上正交。
证明如下:
显然可知,需要证明以下公式成立:

第1第2式可视为三角函数Cos和Sin与1相乘的积分;第3-5式则为sin和cos的不同组合相乘的积分式。
除了这5个式子外,不可能再有其他的组合了。注意,第4第5两个式中,k不能等于n,否则就不属于“三角函数系中任意两个不同函数”的定义了,变成同一函数的平方了。但第3式中,k与n可以相等,相等时也是二个不同函数。
下面通过计算第4式的定积分来验证其正确性,第4式中二函数相乘可以写成:

当 k≠n 时,有:
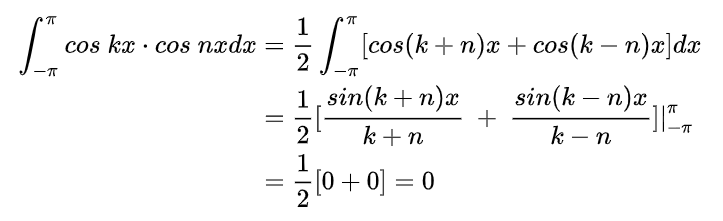
可见在指定[-π, π]的区间里,该式的定积分为0。其他式也可逐一验证。
3、傅里叶级数公式的系数求解
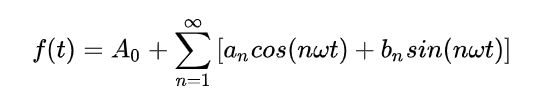
那么对于上述级数,我们该怎么样求解各个系数呢?
求解系数的方法就是消项,比如对于a0的求解,我们只需要把除了a0以外等式所有的项全部消掉不就可以了吗,那么怎么消呢,很容易,a0是唯一一个不包含三角函数的系数,而其他项的三角函数的周期均为2π(注意:我说的是周期,而不是最小周期,其实cosx的周期是2π,cos2x周期为π,……cosnx的周期为2π/n,不过大家周期的最小公倍数都是2π,所以2π是所有这些三角函数的周期),所以我们只需要对等式两端同时进行-π到π的一个积分,就会只留下a0,处理过程是这样:
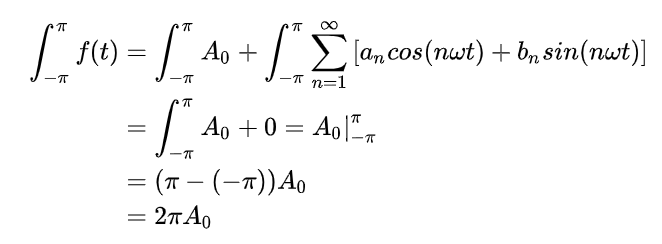
解得:
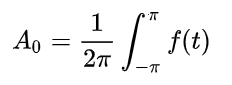
这就求得了第一个系数A0的表达式,接下来再求an和bn的表达式,这里要应用到三角函数系的正交法则,举个例子,比如我们要求解an的值,就意味我们必须把除了an以外所有项都消掉,而an和cosnx相乘,所以我们让整个式子乘上cosnx再积分,利用正交性消去其他项:
这里的公式有一点问题,积分上下限是-π到π的话,应该是对wt进行积分的,但这里写成了对t积分
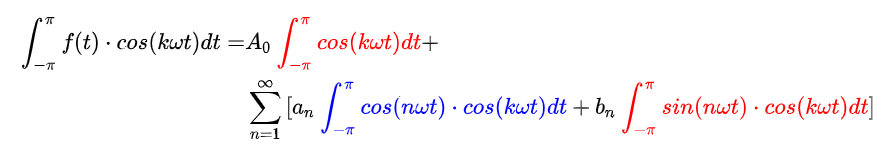
根据三角函数系的正交性,红色积分为0,蓝色项中仅当 k=n 时积分不为0,其余项积分为0,所以有:
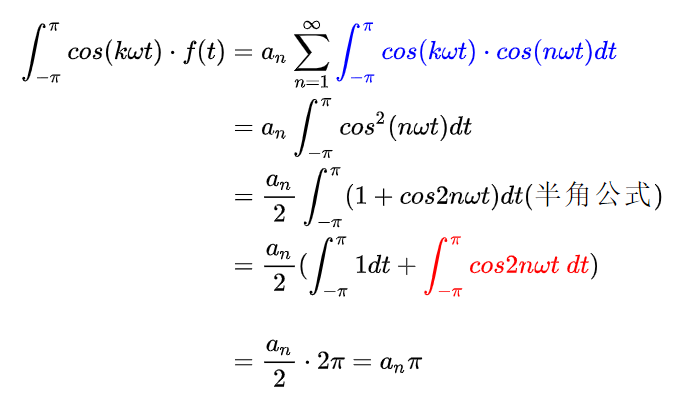
解得:
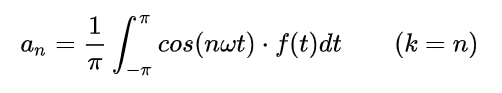
同理两边乘sinnx再积分,可以解得bn:
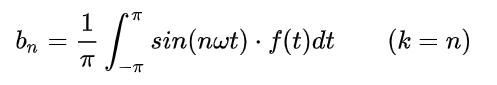
我们发现 A0 的分母为 2pi 而 an、bn 为 pi ,为了统一分母我们令 a0 = 2A0,因此有:
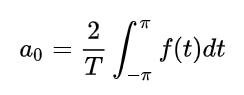
所以级数公式变形为:
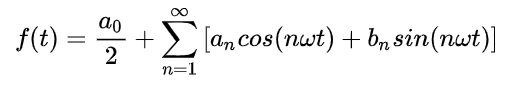
代入T=2pi之后,我们可以得到:

4、傅里叶级数指数形式
根据欧拉公式有:
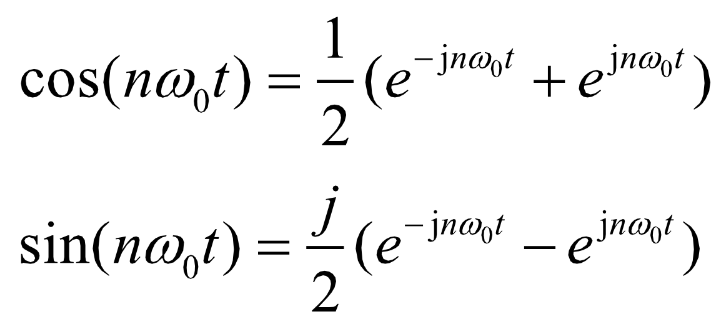
因此代入后有:
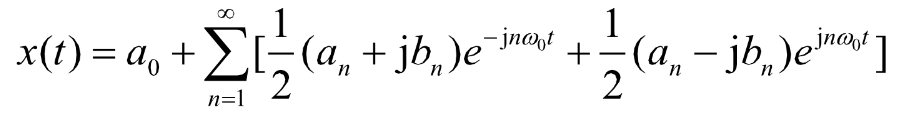
令:
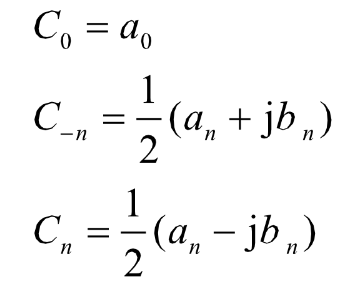
可得:
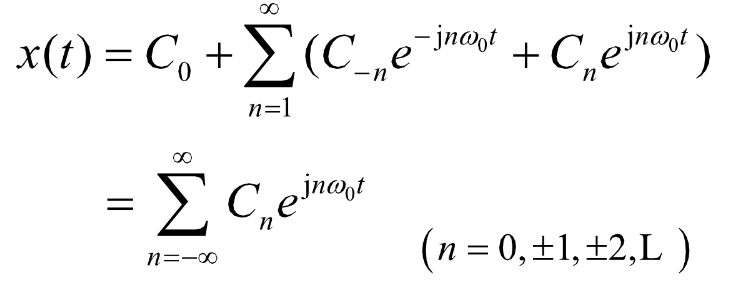
其中:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号