视觉SLAM十四讲 学习笔记7——ch7视觉里程计

 

 

 

3D-2D：PnP问题

　　描述了当知道n个3D空间点及其投影位置时，如何估计相机的位姿。

　　PnP 问题有很多种求解方法，例如：用 3 对点估计位姿的P3P、直接线性变换DLT、EPnP(Efficient PnP) 、UPnP等等。此外,还能用非线性优化的方式，构建最小二乘问题并迭代求解，也就是万金油式的 Bundle Adjustment。

直接线性变换（DLT）：（忽略掉了R和t的内在约束）

　　根据相机的投影原理，有如下公式：

 

 

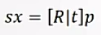
　　其中，P为空间点的其次坐标，P = (X, Y, Z, 1)^T 。x为投影平面上的齐次坐标 x = (u 1 , v 1 , 1)^T

　　展开后如下：　　　　

 

 

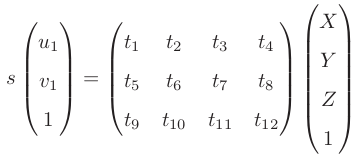
 　　可以得到3个方程，用最后一个方程带入前两个，消除s变量，则一个特征点提供了两个方程，如下：

 

 

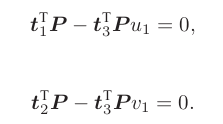
　　其中t为未知量（共12个），则需12个方程，也就是6个特征点，才可以求解（超定时求最小二乘解）

　　这种做法（DLT），将R，t看成独立的未知量（忽略了内在的约束），所以在求出结果之后，需要将t组成的矩阵投影回SO(3)（通常用QR分解来实现）。

P3P：利用3对点求相机外参

 

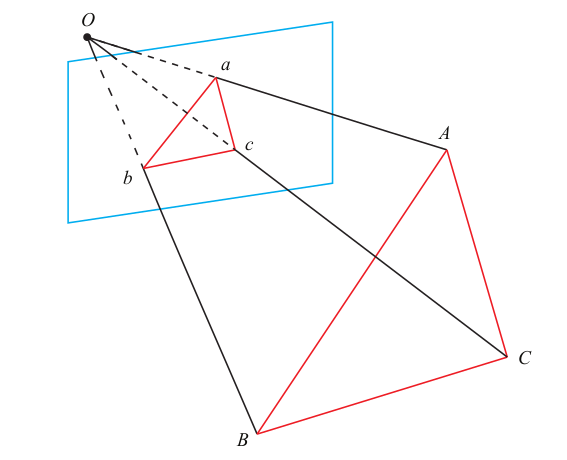
　　根据余弦定理：

 

　　对以上三式全体除以 OC² ， 并且记 x = OA/OC， y = OB/OC，得：

 

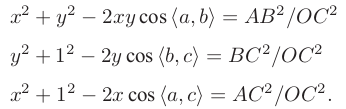
 　　记 v = AB²/OC² ，uv = BC² /OC² ，wv = AC² /OC^2，有：

 

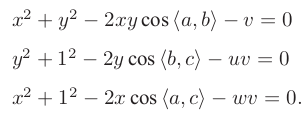
 　　消v，得：

 

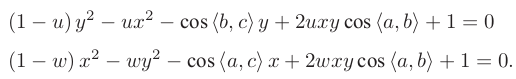
　　余弦值已知，u、w已知，所以是二元二次方程，可解（吴氏消元法）

　　最后，得到x、y后，带入下式：

 

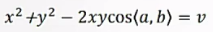
　　解得v，从而得到OC的长度，进而得到各点的距离。

　　所以，我们得到了3D-3D的点对，进而可以计算ICP，见下文。

PnP的优化解法：Bundle Adjustment　　

　　前面说的线性方法，往往是先求相机位姿，再求空间点位置，而非线性优化则是把它们都看成优化变量，放在一起优化。这是一种非常通用的求解方式，我们可以用它对 PnP 或 ICP 给出的结果进行优化。在 PnP 中，这个 Bundle Adjustment 问题，是一个最小化重投影误差(Reprojection error)的问题。

　　考虑 n 个三维空间点 P 及其投影 p，我们希望计算相机的位姿 R,、t，它的李代数表示为 ξ。假设某空间点坐标为 P_i = [ X _i, Y _i, Z_i ]^T ，其投影的像素坐标为 u _i =  [ u_i，v_i]^T，则有：

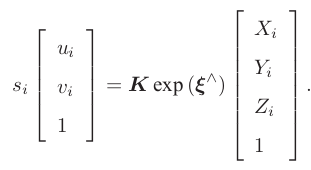
　　即：

　　中间隐含着的齐次坐标到非齐次的转换，否则按矩阵的乘法来说，维度是不对的。

 　　由于相机位姿未知及观测点的噪声，该等式存在一个误差。因此，我们把误差求和，构建最小二乘问题，然后寻找最好的相机位姿，使它最小化：

 

 

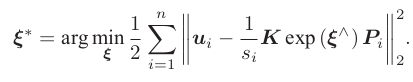
 　　该问题的误差项，是将像素坐标(观测到的投影位置)与 3D 点按照当前估计的位姿进行投影得到的位置相比较得到的误差，所以称为重投影误差。

 

　　在考虑优化问题时，之前提到的求导的问题就派上用场了，对于一个比较抽象的优化问题，通过求导可以判断优化的方向。

　　对于相机位姿的优化：误差对位姿的李代数求导

　　当 e 为像素坐标误差(2 维)，x 为相机位姿(6 维)时，J 将是一个 2 × 6 的矩阵。

　　使用扰动模型求求取李代数的导数，记变换到相机坐标系下的空间点坐标为 P ′ ，并且将其前 3 维取出来：

 

 

 　　相机投影模型相对于 P ′ 为：

 

 

　　展开：　　

 

 

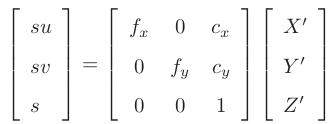
 　　消去 s(实际上就是 P ′ 的距离)，得：

 

 

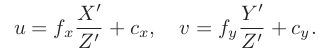
　　利用链式法则对扰动模型求导：

 

 

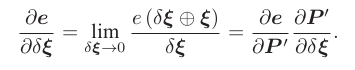
 　　第一个因子是误差关于投影点的导数，易知：

 

 

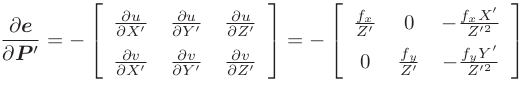
 　　第二个因子为变换后的点关于李代数的导数，由于公式：

 

 

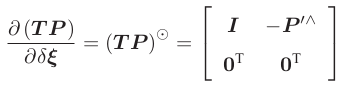
　　其中T为对P点进行的变换，变换后的点即为P'。

　　在 P' 中只取前3维，可以得到：

 

 

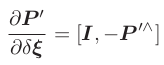
 　　两个因子相乘，得到了一个2X6的雅克比矩阵：

 

 

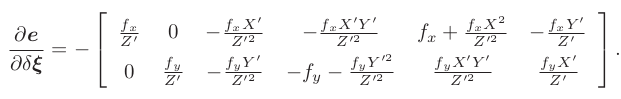
　　对于特征点的空间位置的优化：误差对空间点P求导 

 

 

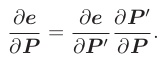
　　第一个因子前面已经得到了计算结果。

　　由于：

 

 　　可以知道，P'对P求导，只剩下R矩阵，于是有：

 

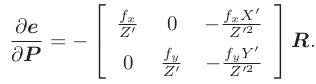
总结：

　　我们推导出了观测相机方程关于相机位姿与特征点的两个导数矩阵。它们十分重要，能够在优化过程中提供重要的梯度方向，指导优化的迭代。