视觉SLAM十四讲 学习笔记4——ch5相机与图像

单目相机模型：

 

 

 

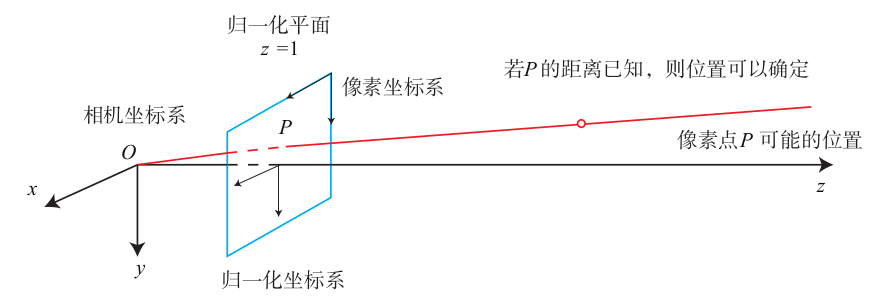
　　针孔相机模型的映射关系：

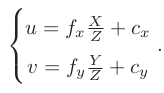
 　　化为矩阵形式：

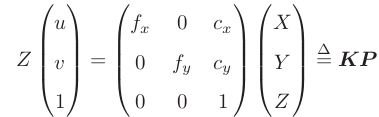
 　　其中，中间的矩阵被称为相机的内参矩阵K。通常认为，相机的内参在出厂之后是固定的，不会在使用过程中发生变化。有点相机生产厂商会告诉你相机的内参，而有时需要你自己确定相机的内参，也就是所谓的标定。（目前标定算法已经比较成熟，如著名的单目棋盘格张友正标定法）

　　（后一个式子隐含了一次齐次坐标到非齐次坐标的转换：T为4X4的矩阵 P_w为3X1的向量）

　　其中,相机的位姿 R, t 又称为相机的外参数(Camera Extrinsics)。相比于不变的内参，外参会随着相机运动发生改变，同时也是 SLAM 中待估计的目标，代表着机器人的轨迹。

 　　投影过程还可以从另一个角度来看。我们可以把一个世界坐标点先转换到相机坐标系，再除掉它最后一维的数值(即该点距离相机成像平面的深度)，这相当于把最后一维进行归一化处理，得到点 P 在相机归一化平面上的投影。

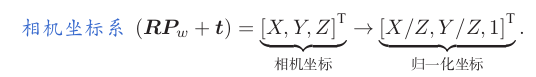
 　　归一化坐标可看成相机前方 Á z = 1 处的平面上的一个点,这个 z = 1 平面也称为归一化平面。

 　　归一化坐标再左乘内参就得到了像素坐标，所以我们可以把像素坐标 [u, v]^T 看成对归一化平面上的点进行量化测量的结果。从这个模型中也可以看出，如果对相机坐标同时乘以任意非零常数，归一化坐标都是一样的，这说明点的深度在投影过程中被丢失了，所以单目视觉中没法得到像素点的深度值。

畸变：

　　由透镜形状引起的畸变称为径向畸变；由于不能使透镜和成像平面严格平行会还会引起切向畸变。　　

　　径向畸变可看成坐标点沿着长度方向发生了变化，也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化。

　　径向畸变多项式描述：

 

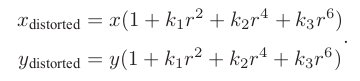
 　　切向畸变多项式描述：

 

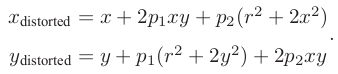
 单目相机成像过程总结：

　　1、首先，世界坐标系下由一个固定的点P，世界坐标为P_w。

　　2、由于相机在运动，他的运动有R，t或变换矩阵T∈SE(3)描述。P的相机坐标为：

 

　　3、这时的P点的相机坐标分量为X、Y、Z，把他们投影带归一化平面Z = 1上，得到P的归一化坐标：

 

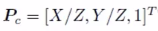
　　4、有畸变时，根据畸变参数计算P_c发生畸变后的坐标。

　　5、最后，P的归一化坐标经过内参后，对应到它的像素坐标P_uv = KP_c

 双目相机模型：

　　

 

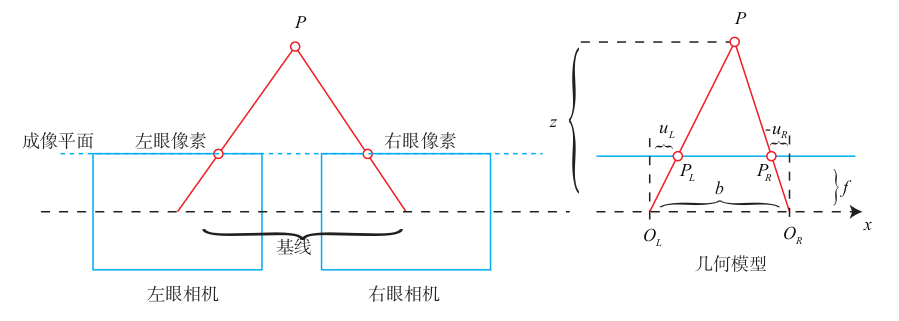
　　可列出下式：　　

 

 　　可推导出：

 

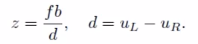
　　其中d为视差，描述同一个点在左右目上成像的距离，d最小为一个像素（制约双目测量z 的量程）。