视觉SLAM十四讲 学习笔记3——ch4李群与李代数
概述：
在实际的SLAM中，我们除了对旋转进行表示之外，还需要对它们进行估计和优化。因为在SLAM中位姿是未知的，而我们需要解决什么样的相机位姿最符合当前的观测数据这样的问题，一种典型的方法是把他们构成一个优化问题，求解最优的的R，t，使误差最小化。
旋转矩阵姿自身是带有约束的（正交且行列式为1）。它们作为优化变量时，会引入额外的约束，使优化变得困难，通过李群——李代数之间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方法。
李群李代数基础：
群（Group）：是一种集合加上一种运算的代数结构。我们把集合记作 A，运算记作·，那么群可以记作 G = (A, ·)
群要求这个运算满足一下几个条件（“封结幺逆”—— 凤姐咬你 ）：
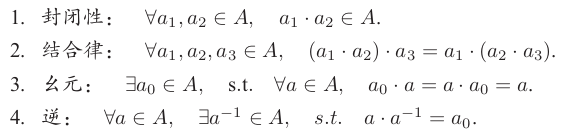
可以验证：旋转矩阵集合和矩阵乘法构成群，变换矩阵和矩阵乘法也构成群。
李群（Lie Group）：具有连续（光滑）性质的群。
SO(3)和SE(3)都是李群，一个刚体能够连续地在空间中运动。但是SO(3)和SE(3)只有定义良好的乘法，没有加法，所以难进行取极限、求导等操作。
李代数：与李群对应的一种结构，位于向量空间，通常记作so(3)和se(3)。
李代数由一个集合V，一个数域F和一个二元运算[，]组成，其中二元运算被称为李括号，李括号表达了两个元素之间的差异，它不要求结合律，而要求元素和自己做李括号之后为零的性质。eg：三维向量上定义的叉积是一种李括号，因此下式构成了一个李代数。
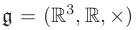
李代数so(3)： SO(3) 对应的李代数是定义在 R3上的向量，我们记作 φ。每个 φ 都可以生成一个反对称矩阵：
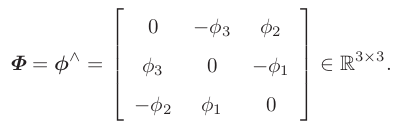
在此定义下,两个向量 φ1, φ2 的李括号为：
由于向量 φ 与反对称矩阵是一一对应的，在不引起歧义的情况下，就说 so(3) 的元素是三维向量或者三维反对称矩阵，不加区别。
它与 SO(3) 的关系由指数映射给定：
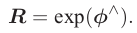
李代数se(3)：
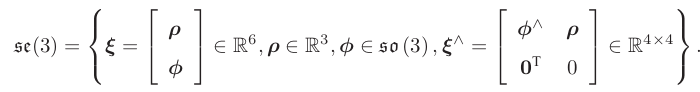
我们把每个 se(3) 元素记作 ξ，它是一个六维向量。前三维为平移(但含义与变换矩阵中的平移不同，分析见后)，记作 ρ；后三维为旋转，记作 φ，实质上是 so(3) 元素。
同时，我们拓展了 ∧ 符号的含义。在 se(3) 中，同样使用 ∧ 符号，将一个六维向量转换成四维矩阵，但这里不再表示反对称：
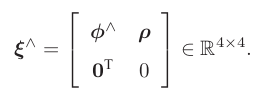
我们仍使用 ∧ 和 ∨ 符号来指代“从向量到矩阵”和“从矩阵到向量”的关系，以保持和 so(3) 上的一致性。它们依旧是一一对应的。读者可以简单地把 se(3) 理解成“由一个平移加上一个 so(3) 元素构成的向量”(尽管这里的 ρ 还不直接是平移)。
se(3)的李括号：
指数映射与对数映射：
so(3)指数映射：
泰勒展开推导指数映射公式
旋转向量——(罗德里格斯公式)——>旋转矩阵
so(3)——(罗德里格斯公式)——>SO(3)
这说明，so(3)的物理意义就是旋转向量，so(3) 实际上就是由所谓的旋转向量组成的空间。
so(3)对数映射：
同样可以使用泰勒展开的方式推导对数映射的公式，但是现在已经知道so(3)和SO(3)分别对应旋转向量和旋转矩阵，那么可以直接使用之前的根据旋转矩阵求解旋转向量的方式得到对数映射（利用迹的性质分别求解转角和转轴）。
se(3)指数映射：
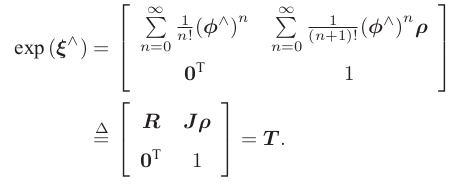
ξ 的指数映射左上角的 R 是我们熟知的 SO(3) 中的元素，与 se(3) 当中的旋转部分 φ 对应。
而右上角变换矩阵的平移部分，与李代数的平移部分相差了一个线性变换J（平移部分经过指数映射之后，发生了一次以J为系数矩阵的线性变换）。
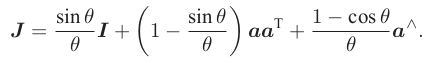
李群李代数指数/对数映射总结：
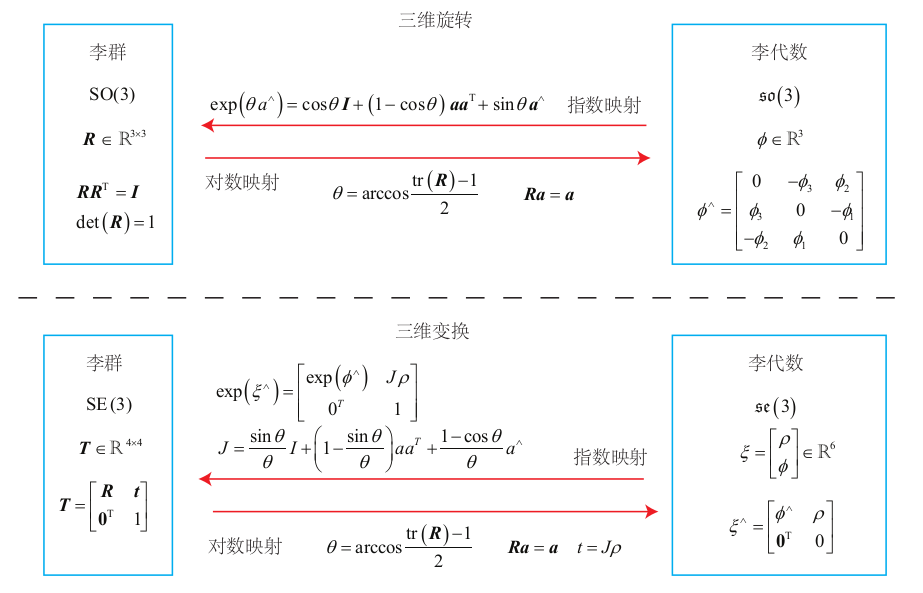
李代数的求导与扰动模型：
背景：使用李代数的一大动机是进行优化，而在优化过程中导数是非常必要的信息。李群元素只有乘法，没有加法，无从定义导数。那么能否利用李代数上的加法，定义李群元素的导数，使用指数映射和对数映射完成变换关系。
当在李代数中做加法是，是否等价于在李群上做乘法？即下式是否成立：
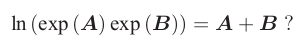
答案：不成立！
上式的完整正确形式由BCH公式给出，很复杂。部分展开式如下：
考虑小量的二次以上项均可忽略掉，可以得到近似的BCH公式：
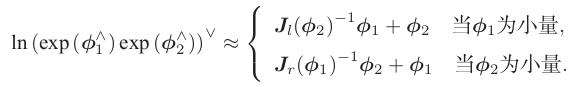
李代数在 BCH 近似下，分成了左乘近似和右乘近似两种，在使用时我们须注意使用的是左乘模型还是右乘模型。
左乘雅克比：
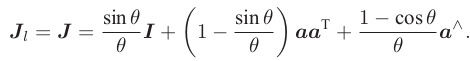
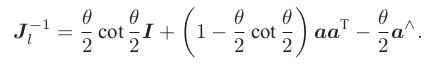
右乘雅克比：（对自变量取负号即可）
李群乘法和李代数加法的关系：
在李群上左乘小量是，李代数上的加法相差左雅克比的逆：
李代数上进行小量加法是，相当于利群上左（右）乘一个带左（右）雅克比的量。
相似地，对应SE(3)，也有类似的BCH近似：（花写雅克比的具体形式这里省略不讲）
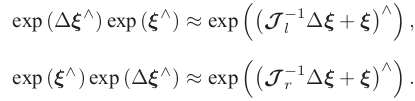李代数求导：
李代数求导有两种思路：
1、对R对应的李代数加上一个小量，求相对于小量的变化率（求导模型）
2、对R左乘或右乘一个小量，求相对于小量的李代数的变化率（扰动模型）（更为简洁实用）
