红黑树的条件是怎么来的——从2-3树到红黑树

前几天学习epoll函数，发现epoll函数使用红黑树结构存储epfd来提高fd检索速度，又想起HashMap中引入了红黑树在达到一定链表长度后转为红黑树来避免链表遍历。

红黑树的应用这么广泛，我们应该对其有所了解。

首先我们应该知道，在无序线性表中查找是否存在某个值需要对线性表进行遍历，其查找时间复杂度为On，但如果线性表是有序的，使用二分法查找，其时间复杂度就会降低为Ologn，让待查找的线性表保持有序显然是有利于查找操作的，但这种便利并不是没有代价的，不论是各种排序算法，还是在构建线性表时就保持有序，都会带来额外的操作，例如MysqlnnoDB使用的多路查找平衡B+树，又或者是我们最熟悉的平衡二叉树，其维护有序的成本都很高，而红黑树，想必大家早就有所耳闻或有所了解，接下来我们详细介绍这种排序树好在哪里，本篇纯属个人理解原创，做交流记录用，仅供参考。

什么是红黑树，红黑树的要求有哪些，本文不再赘述，网上找到的文章都有答案，了解到红黑树的结构和条件后，会发现，与二叉平衡树非常相似，只是平衡的条件和要求不同，这也是我一直以来的疑惑，二叉平衡树的逻辑很好理解，通过旋转来达到平衡条件，使得最大查找长度为logn，那为什么epoll和hashMap不直接使用AVL树呢？我认为最终要的原因就是AVL的平衡条件太苛刻，左右子树的高度差不能超过1，否则就要出发复杂的rebalance操作，从实际使用的角度来看，在n较大的情况下logn和logn + 1的查找效率差别不大，反而因为苛刻条件而导致的开销不能功过相抵，在写操作频繁的操作中，AVL似乎并不能很好的适应，换句话说，AVL树太完美了，也太敏感了。

相信大家和我有一样的疑惑，红黑树的那些平衡条件是怎么总结出来的，似乎并不是AVL这种顺应逻辑的条件，更像是推导出来的条件，因此，我们从rbt的近亲--2-3树说起。

2-3树，大家也有所耳闻，2-3树存在三种节点，第一种是2-节点，数据域有一个值，指针域有两个值；第二种是3-节点，数据域有2个值，指针域有3个值；还有一种是空节点，如下图所示：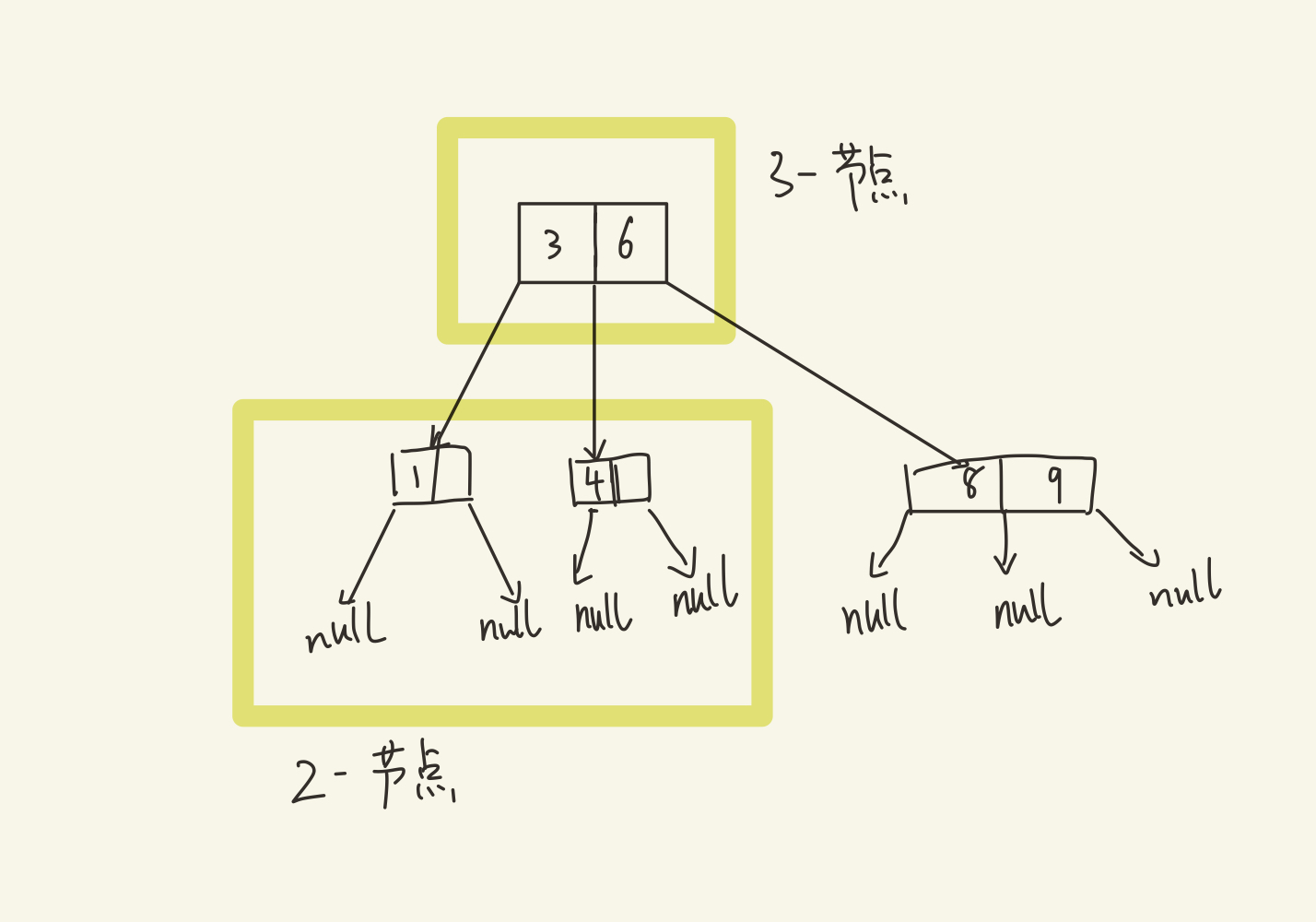

 

2-3树的插入和构建过程如下图所示，可参考：https://www.cnblogs.com/eniac12/p/5558848.html，介绍的很详细

 

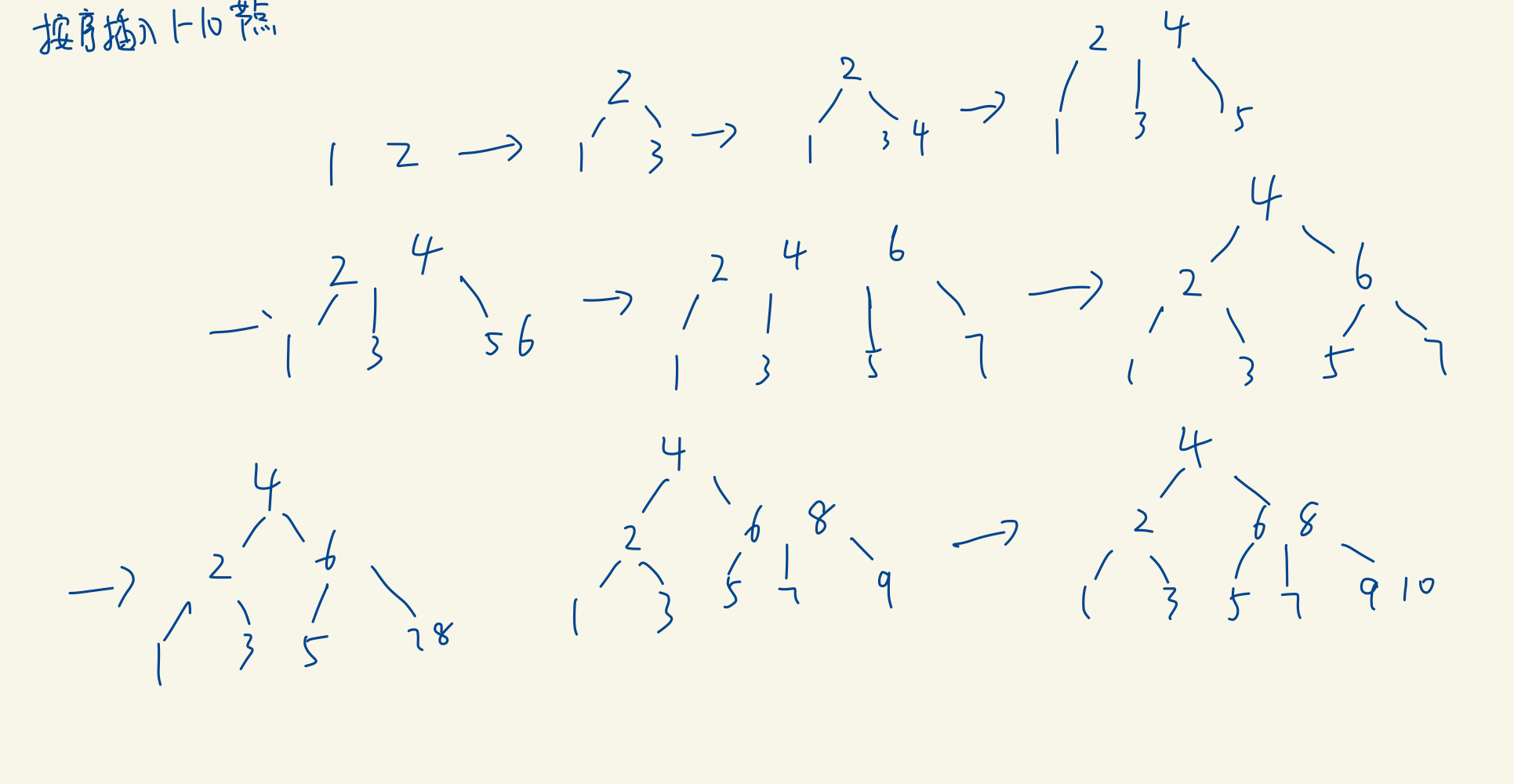
 可以知道的是，2-3树在插入过程中不断增长出新的根，使得树的高度不断增高，底层节点高度永远相等，忽略2节点和3节点的差异后会发现这是一颗完全二叉树，

所有节点的高度都相等，是一颗完美的AVL树

如果我们将其全部的3节点展开，展开时通过红色边链接展开后的子节点构造成一颗二叉树，将上图最终构建的2-3树按照刚才的思路展开如下图所示：

 

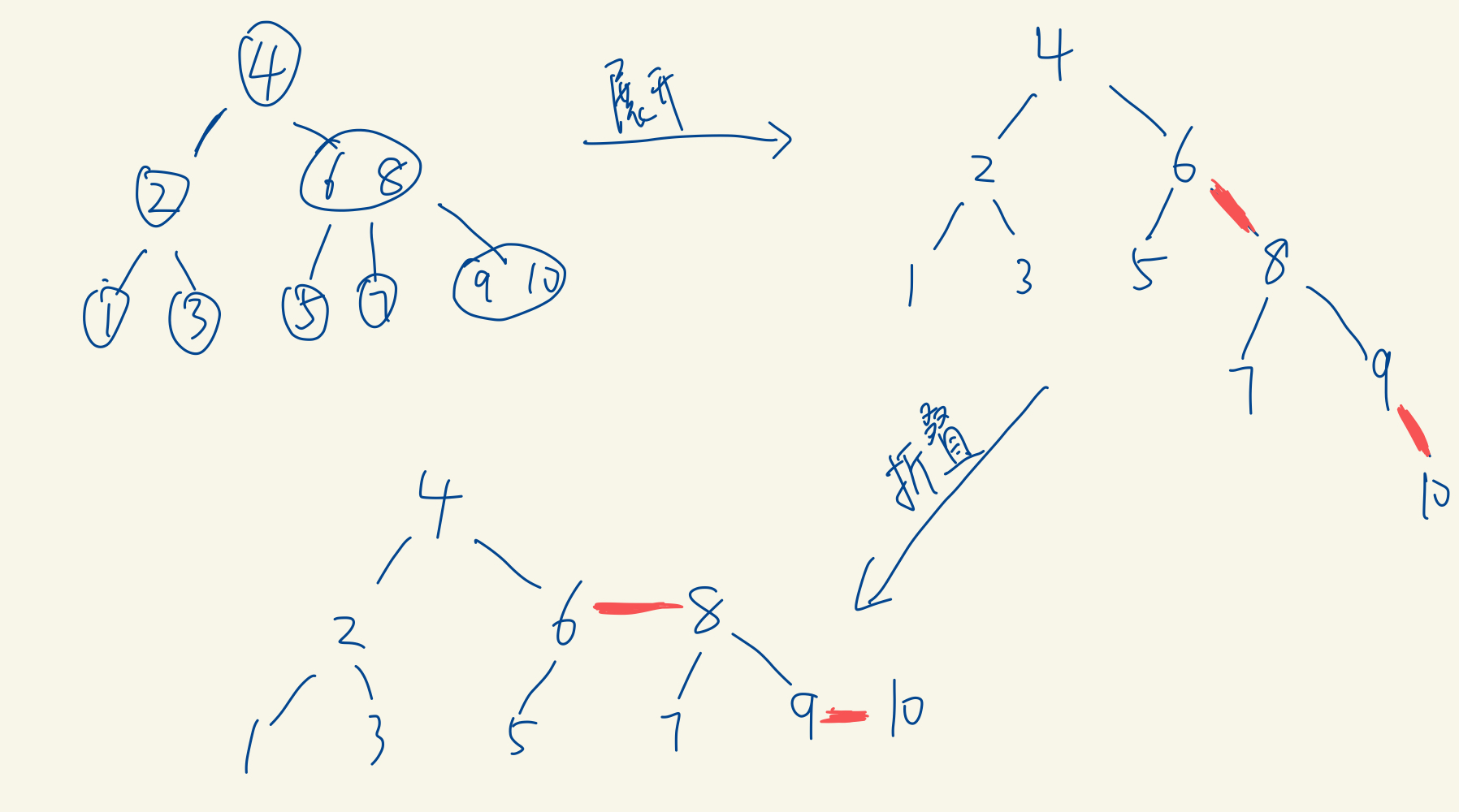
 如果我们把当前节点同父节点之间的边的颜色计作节点的颜色，则会变成下图所示：

 

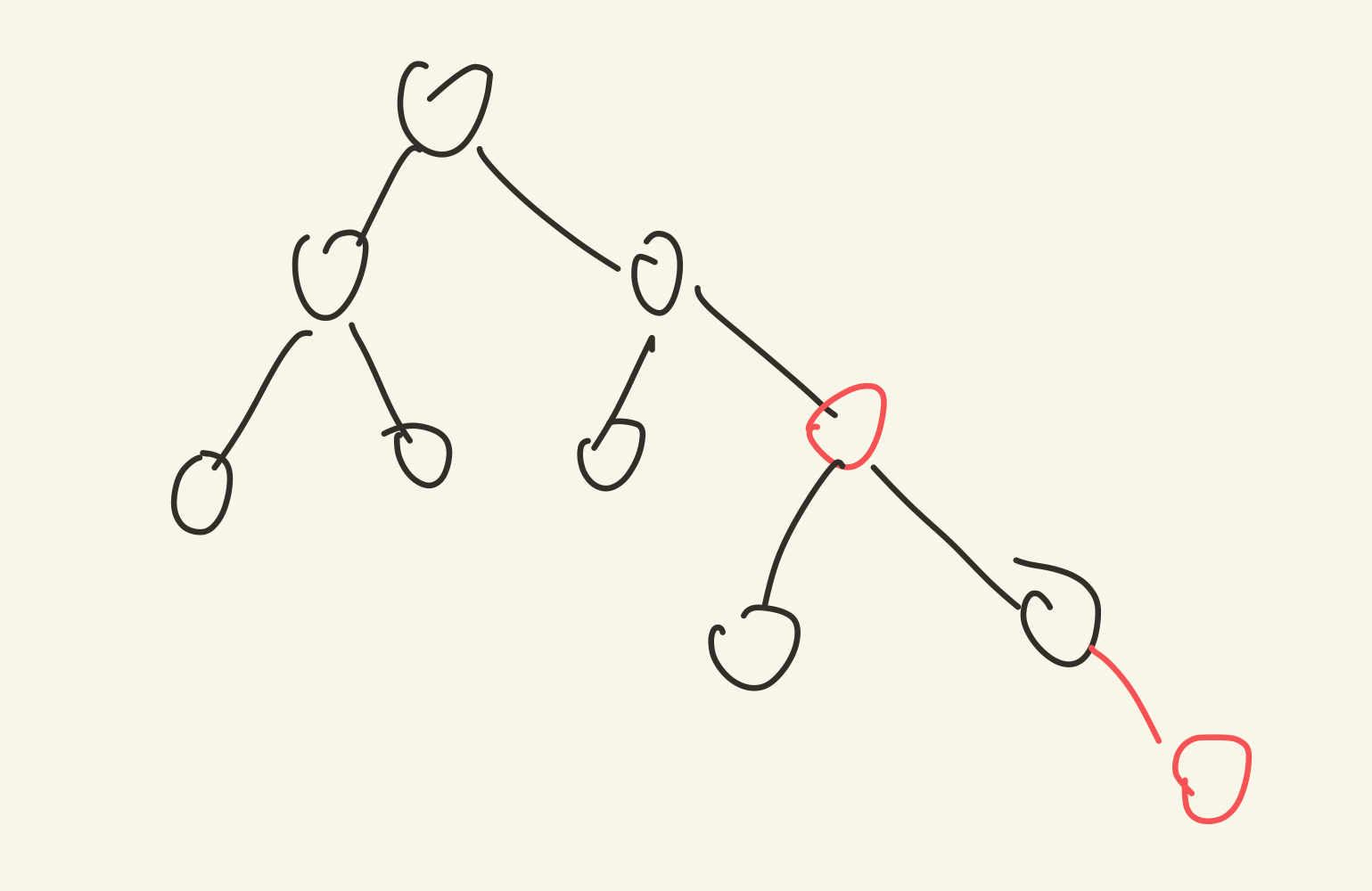
这就是这颗2-3树唯一对应的rbt，由上图展开前的情况可知，未展开红色节点前，所有节点的高度完全一致，展开红色节点后，忽略掉红色节点，所有节点的黑高就是完全一致的，

这就是红黑二叉树的性质之一：所有节点的黑高一致。

由展开过程和分配节点颜色可知只有父节点原来是3节点时，才会将一个父节点中的一个染色为红色，但是展开后，该红色父节点变成了2节点，不会对该节点进行展开操作，所以该节点的子节点一定是黑色，

这就是红黑树的第二条性质：不会存在连续的两个红色节点，或者说，红色节点的子节点必为黑色节点。

根据这些性质，保证了展开后的红黑树的最长查找路径不会超过最短路径的2倍，同时没有AVL树那么敏感，像上图插入10号节点后已经不满足AVL的定义需要调整了，在操作节点频繁的情况下，rbt带来的开销要比AVL小。

如果是查多操作少的情况，则AVL树的稳定性更好。