范数与距离的关系以及在机器学习中的应用
范数与距离的关系以及在机器学习中的应用 - CSDN博客
http://blog.csdn.net/kingzone_2008/article/details/15073987
1 范数
向量的范数可以简单形象的理解为向量的长度,或者向量到零点的距离,或者相应的两个点之间的距离。
向量的范数定义:向量的范数是一个函数||x||,满足非负性||x|| >= 0,齐次性||cx|| = |c| ||x|| ,三角不等式||x+y|| <= ||x|| + ||y||。
常用的向量的范数:
L0范数:||x||0为x向量各个非零元素的个数.(from: http://blog.csdn.net/jihengshan/article/details/19768395)
L2范数: ||x||为x向量各个元素平方和的1/2次方,L2范数又称Euclidean范数或者Frobenius范数
Lp范数: ||x||为x向量各个元素绝对值p次方和的1/p次方
L∞范数: ||x||为x向量各个元素绝对值最大那个元素的绝对值,如下:
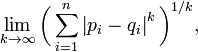
椭球向量范数: ||x||A = sqrt[T(x)Ax], T(x)代表x的转置。定义矩阵C 为M个模式向量的协方差矩阵, 设C’是其逆矩阵,则Mahalanobis距离定义为||x||C’ = sqrt[T(x)C’x], 这是一个关于C’的椭球向量范数。
2 距离
欧式距离(对应L2范数):最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中。n维空间中两个点x1(x11,x12,…,x1n)与 x2(x21,x22,…,x2n)间的欧氏距离:
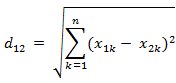
也可以用表示成向量运算的形式:
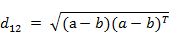
曼哈顿距离:曼哈顿距离对应L1-范数,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上,坐标(x1, y1)的点P1与坐标(x2, y2)的点P2的曼哈顿距离为: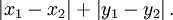 ,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
切比雪夫距离,若二个向量或二个点x1和x2,其坐标分别为(x11, x12, x13, ... , x1n)和(x21, x22, x23, ... , x2n),则二者的切比雪夫距离为:d = max(|x1i - x2i|),i从1到n。对应L∞范数。
闵可夫斯基距离(Minkowski Distance),闵氏距离不是一种距离,而是一组距离的定义。对应Lp范数,p为参数。
闵氏距离的定义:两个n维变量(或者两个n维空间点)x1(x11,x12,…,x1n)与 x2(x21,x22,…,x2n)间的闵可夫斯基距离定义为:

其中p是一个变参数。
当p=1时,就是曼哈顿距离,
当p=2时,就是欧氏距离,
当p→∞时,就是切比雪夫距离,
根据变参数的不同,闵氏距离可以表示一类的距离。
Mahalanobis距离:也称作马氏距离。在近邻分类法中,常采用欧式距离和马氏距离。
3 在机器学习中的应用
L1范数和L2范数,用于机器学习的L1正则化(Regularization)、L2正则化。对于线性回归模型,使用L1正则化的模型建叫做Lasso回归,使用L2正则化的模型叫做Ridge回归(岭回归)。
其作用是:
L1正则化是指权值向量w中各个元素的绝对值之和,可以产生稀疏权值矩阵(稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0. ),即产生一个稀疏模型,可以用于特征选择;
L2正则化是指权值向量w中各个元素的平方和然后再求平方根,可以防止模型过拟合(overfitting);一定程度上,L1也可以防止过拟合。
至于为什么L1正则化能增加稀疏性,L2正则化能防止过拟合,原理可查看参考资料。
参考资料:
http://blog.csdn.net/v_july_v/article/details/8203674
http://blog.csdn.net/jinping_shi/article/details/52433975
==============================
L1/L2正则化(Regularization)
什么是 L1/L2 正则化 (Regularization)
https://zhuanlan.zhihu.com/p/25707761





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具