C# 计算地图上某个坐标点的到多边形各边的距离

在判断了某个坐标点是否在多边形内后，还有另一个需求就是当我这个坐标点在多边形外部时，我需要计算这个坐标点到多边形的距离是否在一个允许的误差范围内

通过两个位置的经纬度坐标计算距离（C#版本）

转自:https://blog.csdn.net/jasonsong2008/article/details/78423496

经纬坐标系中求点到线段距离的方法

转自C语言版本: https://blog.csdn.net/ufoxiong21/article/details/46487001

依据地图上的经纬度坐标计算某个点到多边形各边的距离

转自JAVA版本 https://blog.csdn.net/james_laughing/article/details/72881056?locationNum=12&fps=1

在一些地图的应用中（如求偏航），常常需要求一个点到一条线程的距离，以判断是否远离航线。然而在经纬度坐标中，并没有类似直角坐标系中的公式来计算。在经纬度中，一般应用最广的公式是求两点距离的方法，如何通过两点之间的距离公式来达到计算出点到线段的方法呢，我们先来看在经纬度中求两点距离的计算方法。

一、经纬度中求两点距离的计算方法

       网上有很多介绍该计算方法，此处不再 一一阐述。在北半球中：

       C = sin(LatA*Pi/180)*sin(LatB*Pi/180) + cos(LatA*Pi/180)*cos(LatB*Pi/180)*cos((MLonA-MLonB)*Pi/180)

       Distance = R*Arccos(C)*Pi/180

       注1：其中LonA、LatA、LonB、LatB分别是A、B两个点的经纬度值，其中三角函数的输入和输出都采用弧度值

       注2：R（地球半径）和Distance单位是相同，如果是采用6378.137千米作为半径，那么Distance就是千米为单位

      C语言代码：

double getDistanceBtwP(double LonA, double LatA,double LonB, double LatB)//根据两点经纬度计算距离,X经度，Y纬度
{
    double radLng1 = LatA * M_PI / 180.0;
    double radLng2 = LatB * M_PI / 180.0;
    double a = radLng1 - radLng2;
    double b = (LonA - LonB) * M_PI/ 180.0;
    double s = 2 * asin(sqrt(pow(sin(a / 2), 2)+ cos(radLng1) * cos(radLng2) * pow(sin(b / 2), 2))) * 6378.137;    //返回单位为公里
    return s;
}

二、经纬坐标中求点到线段的距离的方法

   在经纬坐标系中，求点C(LonC,LatC)到以点A(LonA,LatA)和点B(LonB,LatB)为端点的线段的距离D。此问题可以分为三种情况：

 

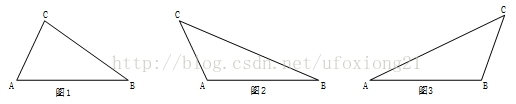
 ①点C在线段AB的正上方时，则距离D=点C到直线AB的垂直距离，如图1；

        ②AC与AB形成钝角时，则距离D=线段AC的长度，如图2；

        ③BC与AB形成钝角时，则距离D=线段BC的长度，如图3；

        1、首先如何判断是属于哪种情况

        我们可以利用勾股定理逆定理的推广，假如AB、BC、AC的长度分别为a，b，c

        ①若b*b+c*c<a*a，则边a所对的角为钝角，即图1的情况；

        ②若a*a+c*c<b*b，则边b所对的角为钝角，即图2的情况；

        ③若a*a+b*b<c*c，则边c所对的角为钝角，即图3的情况；

        2、求图1情况的距离D

        我们希望可以通过距离公式即可求出距离D，从而联想到海伦公式。

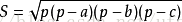
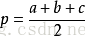
       在海伦公式中，三角形的面积，其中，则距离D=2S/a;

三、计算方法总结

       对于图1情况以及计算出，对于图2和图3的计算均已转换为两个点之间的距离公式，此处不再累赘。因此，在经纬度坐标系中，求点到线段的距离的C语言代码如下：

//点PCx,PCy到线段PAx,PAy,PBx,PBy的距离
double GetNearestDistance(double PAx, double PAy,double PBx, double PBy,double PCx, double PCy)
{     
    double a,b,c;  
    a=getDistanceBtwP(PAy,PAx,PBy,PBx);//经纬坐标系中求两点的距离公式
    b=getDistanceBtwP(PBy,PBx,PCy,PCx);//经纬坐标系中求两点的距离公式
    c=getDistanceBtwP(PAy,PAx,PCy,PCx);//经纬坐标系中求两点的距离公式
    if(b*b>=c*c+a*a)return c;   
    if(c*c>=b*b+a*a)return b;  
    double l=(a+b+c)/2;     //周长的一半   
    double s=sqrt(l*(l-a)*(l-b)*(l-c));  //海伦公式求面积 
    return 2*s/a;   
}

 

好了上面是引用的C语言版本的逻辑,我们可以了解了基本的计算逻辑

下面是我经过简单修改过后的C#版本

  //地球半径，单位米
        private const double EARTH_RADIUS = 6378137;

        /// <summary>
        /// 判断是否在误差范围内
        /// </summary>
        /// <param name="point"></param>
        /// <param name="points"></param>
        /// <param name="limitDistance"></param>
        /// <returns></returns>
        public static bool InLimitDistance(location point, List<location> points, double limitDistance)
        {
            List<double> distance=new List<double>();
            var len = points.Count;
            var maxIndex = len - 1;
            for (int i = 0; i < len; i++)
            {
                //多边形中当前点
                var currentPoint = points[i];
                var nearPoint = maxIndex == i ? points[0] : points[i + 1];
                double a, b, c;
                a = GetDistance(point, currentPoint);//经纬坐标系中求两点的距离公式
                b = GetDistance(point, nearPoint);//经纬坐标系中求两点的距离公式
                c = GetDistance(currentPoint, nearPoint);//经纬坐标系中求两点的距离公式
                if (b * b >= c * c + a * a)
                {
                    distance.Add(c);
                    continue;
                  
                }
                 if (c * c >= b * b + a * a)
                {
                    distance.Add(b);
                    continue;
                }

                double l = (a + b + c) / 2;     //周长的一半
                double s = Math.Sqrt(l * (l - a) * (l - b) * (l - c));  //海伦公式求面积 
                distance.Add(2 * s / a);
            }

            if (!distance.Any())
            {
                return false;
            }

            var count = distance.Where(s => s < limitDistance).Count();
            if (count > 0) return true;
            return false;
        }
        /// <summary>
        /// 计算两点位置的距离，返回两点的距离，单位：米
        /// 该公式为GOOGLE提供，误差小于0.2米
        /// </summary>
        /// <param name="lng1">第一点经度</param>
        /// <param name="lat1">第一点纬度</param>        
        /// <param name="lng2">第二点经度</param>
        /// <param name="lat2">第二点纬度</param>
        /// <returns></returns>
        private static double GetDistance(location point1, location point2)
        {
            double radLat1 = Rad(point1.lat);
            double radLng1 = Rad(point1.lng);
            double radLat2 = Rad(point2.lat);
            double radLng2 = Rad(point2.lng);
            double a = radLat1 - radLat2;
            double b = radLng1 - radLng2;
            double result = 2 * Math.Asin(Math.Sqrt(Math.Pow(Math.Sin(a / 2), 2) + Math.Cos(radLat1) * Math.Cos(radLat2) * Math.Pow(Math.Sin(b / 2), 2))) * EARTH_RADIUS;
            return result;
        }

        /// <summary>
        /// 经纬度转化成弧度
        /// </summary>
        /// <param name="d"></param>
        /// <returns></returns>
        private static double Rad(double d)
        {
            return (double)d * Math.PI / 180d;
        }